高等数学第二章导数知识总结
高等数学第二章知识总结
在这一章里需要掌握的是求一阶导数的多种方法和求高阶导数的计算公式。微分和导数的关系
求导数与求微分方法相同,只不过在求微分时要在后面加上dx.
函数在某点处的导数就是函数在该点处的变化率. 导数有很多种表现形式.
一.
(1) 单侧导数 即左 右导数.
函数可导的充要条件是:左右导数存在且相等.
(2) 可导与连续的关系:可导必然连续,连续不一定可导.
注:函数的导数就是函数在某点处因变量与自变量比值的极限.
◆求导数的方法有:
(1) 利用导数的定义.(简单一点就是△y/△x的极
限)
(2) 利用导数的几何意义解决几何及物理,化学的
实际问题.
(3) 利用初等函数的求导公式.(在书P59)
(4) 利用反函数求导法.(反函数的导数就是原函数
导数的倒数.)
(5) 利用复合函数求导法.(由外到内,逐层求导)
(6) 利用隐函数求导法
(7) 利用参数方程确定函数的求导法.
(8) 利用分段函数求导法.
(9) 利用函数连续,可导的定义,研究讨论函数的连
续性与可导性.
二.高阶导数
高阶导数可细分为:一阶导数,二阶导数,三阶导数……N阶导数等等.(一阶导数的导数是二阶导数) 应该掌握的是高阶导数的运算.
方法有两种:(1)直接法.(2)间接法.
间接法适用于阶数较高的运算.其规律性较强. 常用的高阶导数公式在书P63上.注意查看.
■计算uv相乘形式的高阶导数时,首先要判断u,v从一阶到n阶的结果,再运用莱布尼兹公式求出结果。
三.隐函数和由参数方程确定的函数的导数 什么是隐函数?
如果变量x,y的函数关系可以用一个二元方程表示,且对在给定范围内的每一个x,通过方程有确定的y与之对应,即Y是X的函数,这种函数就叫做隐函数
F(x,y)=0
从二元方程中解出y的值,就是隐函数的显化. 有些隐函数不易显化,甚至不能显化.
隐函数的求导方法:(例题在书P66 例40,41)
(1) 把y看做是复合函数的中间变量,把y看作y(x)
即可。再在方程两边分别对X求导.
(2) 从求导后的方程中求出y’.
(3) 在隐函数的求导结果中允许含有y,但是求某一
以知点的导数时不仅要代X的值,还要代Y的值. 对数求导法:先两边取对数,再关于X求导.例题在书P68,例44(遇到指数形式的函数时就采用此类方法)
对参数方程确定的函数求导方法很简单,就是用y’/x’.
四.函数的微分.
可微就可导,可导就可微.
求函数的微分就是对函数求导,主要就是在所求结果后面加上dx.
微分的几何意义是某点处的切线纵坐标的增量.
常用的微分公式在书P76.
五.微分的应用.
1.微分在近似计算,误差估计中的应用.在书P80 P81.
第二篇:高等数学第五章_定积分总结
第五章 定积分
创新生技102班 张梦菲
2010015066
一、 主要内容
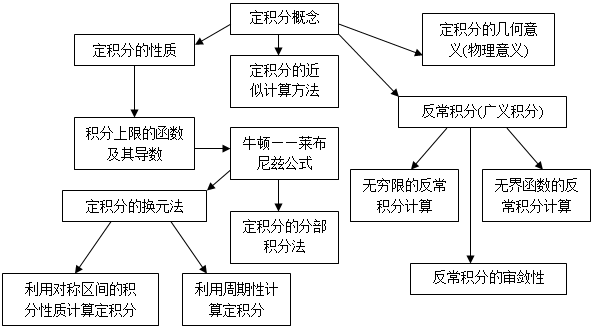
Ⅰ. 定积分概念:
- 定积分定义:设
 在区间
在区间 上有界,在
上有界,在 中任意插入若干个分点
中任意插入若干个分点
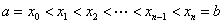 .把
.把 分成
分成 个小区间
个小区间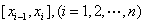 ,小区间的长度记为
,小区间的长度记为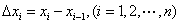 ,在
,在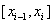 上任意取一点
上任意取一点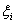 ,作
,作 ,若
,若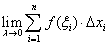
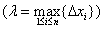 存在. 就称该极限为
存在. 就称该极限为 在
在 上的定积分.
上的定积分.
记为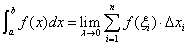
当上述极限存在时,称 在
在 上可积.
上可积.
- 若
 在
在 上连续,则
上连续,则 在
在 上可积。
上可积。 - 若
 在
在 上有界,且只有有限个间断点,则
上有界,且只有有限个间断点,则 在
在 上可积.
上可积.
Ⅱ. 定积分的几何意义
定积分 在几何上表示:由曲线
在几何上表示:由曲线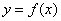 ,直线
,直线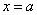 和
和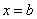 以及
以及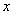 轴所围图形面积的代数和 (
轴所围图形面积的代数和 (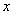 轴上方的面积取正,
轴上方的面积取正,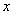 轴下方的面积取负)
轴下方的面积取负)
Ⅲ. 定积分的性质
1. 补充规定:(1)当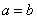 时,
时,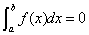
(2)当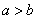 时,
时, 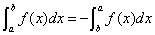
2. 性质:
(1) 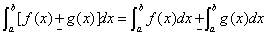
(2) 
(3) 
(4)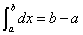
(5) 若在 上,
上,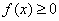 ,则
,则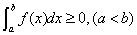
推论1:若在 上,
上,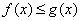 ,则
,则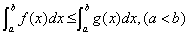 .
.
推论2: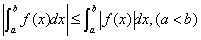 .
.
(6 ) 若在 上,
上, ,则
,则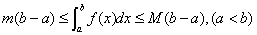
(7) (定积分中值定理):若 在
在 上连续,则在
上连续,则在 上至少存在
上至少存在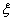 ,使
,使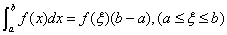 .
.
3. 连续函数 在
在 上的平均值,
上的平均值,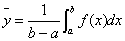
Ⅳ. 积分上限函数及其导数
1. 若对任意 ,
,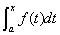 存在,则称
存在,则称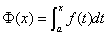 为积分上限的函数.
为积分上限的函数.
2. 若 在
在 上可积,则
上可积,则 在
在 上有界. 且积分上限函数
上有界. 且积分上限函数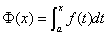 在
在 上连续.
上连续.
3. 设 在
在 上连续,则
上连续,则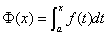 在
在 上可导,且
上可导,且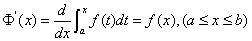 .
.
4. 设 连续,
连续, 可导,则
可导,则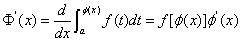 .
.
5. 设 连续,
连续, ,
,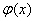 可导,则
可导,则
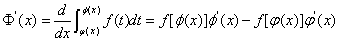 .
.
Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)
设 在
在 上连续,
上连续,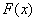 为
为 在
在 上的一个原函数,则
上的一个原函数,则
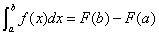 .
.
Ⅵ. 定积分的换元法
设 在
在 上连续,
上连续,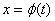 满足:
满足:
(1)  .
.
(2)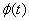 在
在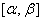 (或
(或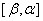 )上具有连续导数,且
)上具有连续导数,且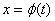 的值域不越出
的值域不越出 的范围,则有
的范围,则有 .
.
注:当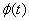 的值域
的值域 越出
越出 的范围,但满足其余条件时,只要
的范围,但满足其余条件时,只要 在
在 上连续,则换元法的结论仍然成立.
上连续,则换元法的结论仍然成立.
Ⅶ. 定积分的分部积分法
设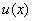 与
与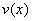 在
在 上具有连续导数,则有
上具有连续导数,则有
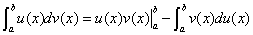
Ⅷ. 几类特殊的积分公式
1. 设 在
在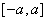 上连续,则有
上连续,则有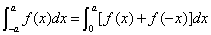 .
.

2. 设 是以
是以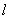 为周期的连续函数,则对任意实数
为周期的连续函数,则对任意实数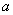 ,
,
有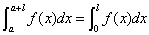 .
.
3. 设 在
在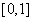 上连续,则
上连续,则
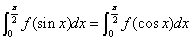

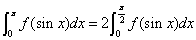
4. 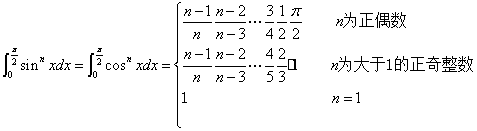
Ⅸ. 反常积分(广义积分)
1. 无穷限的反常积分
(1) 设 在
在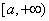 上连续,
上连续, 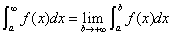
(2) 设 在
在 上连续,
上连续, 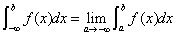
(3) 设 在
在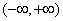 上连续,
上连续,
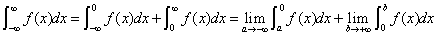
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有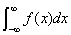 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在,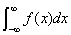 就发散.
就发散.
2. 无界函数的反常积分
(1) 设 在
在 上连续,点
上连续,点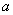 为
为 的瑕点,
的瑕点,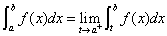
(2) 设 在
在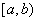 上连续,点
上连续,点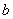 为
为 的瑕点,
的瑕点,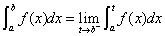
(3) 设 在
在 上除点
上除点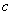
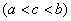 外连续,点
外连续,点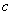 为
为 的瑕点,
的瑕点,
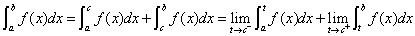
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在, 就发散.
就发散.
3. 反常积分的审敛法
(1) (比较审敛法1) 设 在
在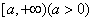 上连续,且
上连续,且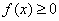 . 若存在常数
. 若存在常数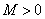 及
及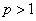 ,使得
,使得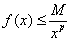
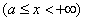 ,则反常积分
,则反常积分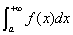 收敛;若存在常数
收敛;若存在常数 ,使得
,使得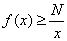
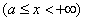 ,则反常积分
,则反常积分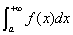 发散.
发散.
(2) (极限审敛法1) 设 在
在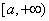 上连续,且
上连续,且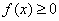 . 若存在常数
. 若存在常数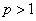 ,使得
,使得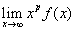 存在,则反常积分
存在,则反常积分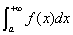 收敛;若
收敛;若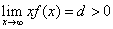 ,
,
(或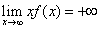 )则反常积分
)则反常积分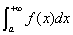 发散.
发散.
(3) (比较审敛法2)设 在
在 上连续,且
上连续,且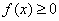 .
. 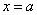 为
为 的瑕点.若存在常数
的瑕点.若存在常数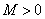 及
及 ,使得
,使得 ,则反常积分
,则反常积分 收敛;若存在常数
收敛;若存在常数 ,使得
,使得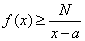
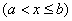 ,则反常积分
,则反常积分 发散.
发散.
(4) (极限审敛法2) 设 在
在 上连续,且
上连续,且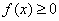 .
. 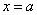 为
为 的瑕点. 若存在常数
的瑕点. 若存在常数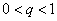 ,使得
,使得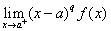 存在,则反常积分
存在,则反常积分 收敛;若
收敛;若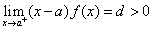 ,(或
,(或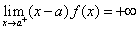 )则反常积分
)则反常积分 发散.
发散.
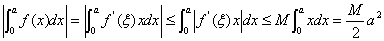 .
.
第三篇:高中数学必修2第二章知识点+习题+答案
第二章直线与平面的位置关系
2.1空间点、直线、平面之间的位置关系
2.1.1
1 平面含义:平面是无限延展的
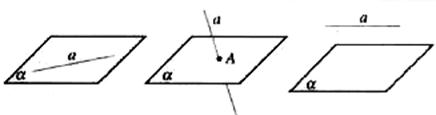
2 平面的画法及表示
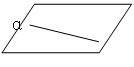
 (1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)
(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)
(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC、平面ABCD等。
3 三个公理:
(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内
符号表示为
 A∈L
A∈L
 B∈L => L α
B∈L => L α
A∈α
B∈α
公理1作用:判断直线是否在平面内
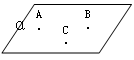 (2)公理2:过不在一条直线上的三点,有且只有一个平面。
(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A、B、C三点不共线 => 有且只有一个平面α,
使A∈α、B∈α、C∈α。
公理2作用:确定一个平面的依据。
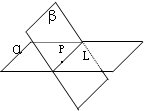 (3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P∈α∩β =>α∩β=L,且P∈L
公理3作用:判定两个平面是否相交的依据
2.1.2 空间中直线与直线之间的位置关系
1 空间的两条直线有如下三种关系:
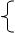
 相交直线:同一平面内,有且只有一个公共点;
相交直线:同一平面内,有且只有一个公共点;
平行直线:同一平面内,没有公共点;
异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a、b、c是三条直线
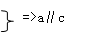 a∥b
a∥b
c∥b
强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补
4 注意点:
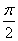 ① a'与b'所成的角的大小只由a、b的相互位置来确定,与O的选择无关,为了简便,点O一般取在两直线中的一条上;
① a'与b'所成的角的大小只由a、b的相互位置来确定,与O的选择无关,为了简便,点O一般取在两直线中的一条上;
② 两条异面直线所成的角θ∈(0, );
③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b;
④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;
⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
2.1.3— 2.1.4 空间中直线与平面、平面与平面之间的位置关系
1、直线与平面有三种位置关系:
(1)直线在平面内 —— 有无数个公共点
(2)直线与平面相交 —— 有且只有一个公共点
(3)直线在平面平行 —— 没有公共点
 指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示
指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示
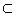 a α a∩α=A a∥α
a α a∩α=A a∥α
2.2.直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:

 a α
a α
 b β => a∥α
b β => a∥α
a∥b
2.2.2平面与平面平行的判定
1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
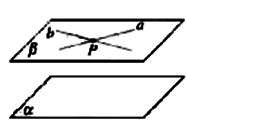
符号表示:
 a β
a β
 b β
b β
a∩b = P β∥α
a∥α
b∥α
2、判断两平面平行的方法有三种:
(1)用定义;
(2)判定定理;
(3)垂直于同一条直线的两个平面平行。
2.2.3— 2.2.4直线与平面、平面与平面平行的性质
1、定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行则线线平行。
符号表示:
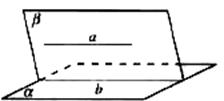
 a∥α
a∥α
 a β a∥b
a β a∥b
α∩β= b
作用:利用该定理可解决直线间的平行问题。
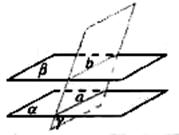 2、定理:如果两个平面同时与第三个平面相交,那么它们的交线平行。
2、定理:如果两个平面同时与第三个平面相交,那么它们的交线平行。
符号表示:
 α∥β
α∥β
α∩γ= a a∥b
β∩γ= b
作用:可以由平面与平面平行得出直线与直线平行
2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
1、定义
如果直线L与平面α内的任意一条直线都垂直,我们就说直线L与平面α互相垂直,记作L⊥α,直线L叫做平面α的垂线,平面α叫做直线L的垂面。如图,直线与平面垂直时,它们唯一公共点P叫做垂足。
 L
L
p
α
2、判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
注意点: a)定理中的“两条相交直线”这一条件不可忽视;
b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想。
2.3.2平面与平面垂直的判定
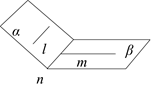
1、二面角的概念:表示从空间一直线出发的两个半平面所组成的图形
A




 梭 l β
梭 l β


 B
B
α
2、二面角的记法:二面角α-l-β或α-AB-β
3、两个平面互相垂直的判定定理:一个平面过另一个平面的垂线,则这两个平面垂直。
2.3.3— 2.3.4直线与平面、平面与平面垂直的性质
1、定理:垂直于同一个平面的两条直线平行。
2性质定理: 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
第二章 点、直线、平面之间的位置关系
A组
一、选择题
1.设?,?为两个不同的平面,l,m为两条不同的直线,且l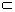 ?,m
?,m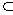
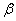 ,有如下的两个命题:①若??∥?,则l∥m;②若l⊥m,则??⊥?.那么( ).
,有如下的两个命题:①若??∥?,则l∥m;②若l⊥m,则??⊥?.那么( ).
A.①是真命题,②是假命题 B.①是假命题,②是真命题
C.①②都是真命题 D.①②都是假命题
2.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( ).
 A.BD∥平面CB1D1
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1角为60°
3.关于直线m,n与平面??,?,有下列四个命题:
①m∥?,n∥??且??∥?,则m∥n; ②m⊥?,n⊥??且??⊥?,则m⊥n;
③m⊥?,n∥??且??∥?,则m⊥n; ④m∥?,n⊥??且??⊥?,则m∥n.
其中真命题的序号是( ).
A.①② B.③④ C.①④ D.②③
4.给出下列四个命题:
①垂直于同一直线的两条直线互相平行
②垂直于同一平面的两个平面互相平行
③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线
其中假命题的个数是( ).
A.1 B.2 C.3 D.4
5.下列命题中正确的个数是( ).
①若直线l上有无数个点不在平面???内,则l∥?
②若直线l与平面???平行,则l与平面???内的任意一条直线都平行
③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行
④若直线l与平面???平行,则l与平面???内的任意一条直线都没有公共点
A.0个 B.1个 C.2个 D.3个
6. 两直线l1与l2异面,过l1作平面与l2平行,这样的平面( ).
A.不存在 B.有唯一的一个 C.有无数个 D.只有两个
7.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为( ).
A.90° B.60° C.45° D.30°
8.下列说法中不正确的是( ).
A.空间中,一组对边平行且相等的四边形一定是平行四边形
B.同一平面的两条垂线一定共面
C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内
D.过一条直线有且只有一个平面与已知平面垂直
9.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果两条直线都平行于一个平面,那么这两条直线互相平行
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直
其中真命题的个数是( ).
A.4 B.3 C.2 D.1
10.异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为( ).
A.[30°,90°] B.[60°,90°] C.[30°,60°] D.[30°,120°]
二、填空题
11.已知三棱锥P-ABC的三条侧棱PA,PB,PC两两相互垂直,且三个侧面的面积分别为S1,S2,S3,则这个三棱锥的体积为 .
12.P是△ABC 所在平面???外一点,过P作PO⊥平面??,垂足是O,连PA,PB,PC.
(1)若PA=PB=PC,则O为△ABC 的 心;
(2)PA⊥PB,PA⊥PC,PC⊥PB,则O是△ABC 的 心;
(3)若点P到三边AB,BC,CA的距离相等,则O是△ABC 的 心;
(4)若PA=PB=PC,∠C=90º,则O是AB边的 点;
 (5)若PA=PB=PC,AB=AC,则点O在△ABC的 线上.
(5)若PA=PB=PC,AB=AC,则点O在△ABC的 线上.
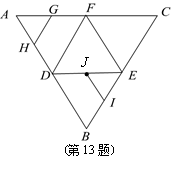
13.如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H,I,J分别为AF,AD,BE,DE的中点,将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为 .
14.直线l与平面??所成角为30°,l∩?=A,直线m∈?,则m与l所成角的取值范围
是 .
15.棱长为1的正四面体内有一点P,由点P向各面引垂线,垂线段长度分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为 .
16.直二面角??-l-??的棱上有一点A,在平面??,??内各有一条射线AB,AC与l成45°,AB ?,AC
?,AC ?,则∠BAC= .
?,则∠BAC= .
三、解答题
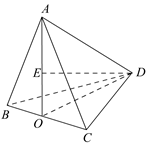
17.在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
(1)求证:BC⊥AD;
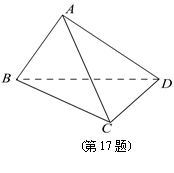 (2)若点D到平面ABC的距离等于3,求二面角A-BC-D的正弦值;
(2)若点D到平面ABC的距离等于3,求二面角A-BC-D的正弦值;
(3)设二面角A-BC-D的大小为?,猜想??为何值时,四面体A-BCD的体积最大.(不要求证明)
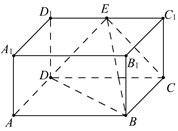 18. 如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.
18. 如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.
(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.

19*.如图,在底面是直角梯形的四棱锥S-ABCD中,AD∥BC,∠ABC=90°,
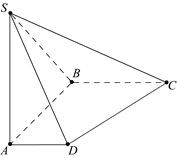 SA⊥面ABCD,SA=AB=BC=1,AD=
SA⊥面ABCD,SA=AB=BC=1,AD=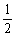 .
.
(1)求四棱锥S—ABCD的体积;
(2)求面SCD与面SBA所成的二面角的正切值.
(提示:延长 BA,CD 相交于点 E,则直线 SE 是
所求二面角的棱.)

(第19题)
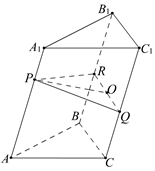 20*.斜三棱柱的一个侧面的面积为10,这个侧面与它所对棱的距离等于6,求这个棱柱的体积.(提示:在 AA1 上取一点 P,过 P 作棱柱的截面,使 AA1 垂直于这个截面.)
20*.斜三棱柱的一个侧面的面积为10,这个侧面与它所对棱的距离等于6,求这个棱柱的体积.(提示:在 AA1 上取一点 P,过 P 作棱柱的截面,使 AA1 垂直于这个截面.)
(第20题)
第二章 点、直线、平面之间的位置关系
参考答案
一、选择题
 1.D 解析:命题②有反例,如图中平面∩平面=直线n,
1.D 解析:命题②有反例,如图中平面∩平面=直线n,
l ?,m
?,m ?,
?,
且l∥n,m⊥n,则m⊥l,显然平面不垂直平面?,??????????????????(第1题)
故②是假命题;命题①显然也是假命题,
2.D解析:异面直线AD与CB1角为45°.
3.D解析:在①、④的条件下,m,n的位置关系不确定.
4.D解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D.
5.B 解析:学会用长方体模型分析问题,A1A有无数点在平面ABCD外,但AA1与平面ABCD相交,①不正确;A1B1∥平面ABCD,显然A1B1不平行于BD,②不正确;A1B1∥AB,A1B1∥平面ABCD,但AB
解析:学会用长方体模型分析问题,A1A有无数点在平面ABCD外,但AA1与平面ABCD相交,①不正确;A1B1∥平面ABCD,显然A1B1不平行于BD,②不正确;A1B1∥AB,A1B1∥平面ABCD,但AB 平面ABCD内,③不正确;l与平面α平行,则l与???无公共点,l与平面???内的所有直线都没有公共点,④正确,应选B. (第5题)
平面ABCD内,③不正确;l与平面α平行,则l与???无公共点,l与平面???内的所有直线都没有公共点,④正确,应选B. (第5题)
6.B解析:设平面 ??过l1,且 l2∥?,则 l1上一定点 P 与 l2 确定一平面 ??,??与 ??的交线l3∥l2,且 l3 过点 P. 又过点 P 与 l2 平行的直线只有一条,即 l3 有唯一性,所以经过 l1 和 l3 的平面是唯一的,即过 l1 且平行于 l2 的平面是唯一的.
7.C解析:当三棱锥D-ABC体积最大时,平面DAC⊥ABC,取AC的中点O,则△DBO是等腰直角三角形,即∠DBO=45°.
8.D解析:A.一组对边平行就决定了共面;B.同一平面的两条垂线互相平行,因而共面;C.这些直线都在同一个平面内即直线的垂面;D.把书本的书脊垂直放在桌上就明确了.
9.B解析:因为①②④正确,故选B.
10.A解析:异面直线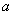 ,
,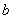 所成的角为60°,直线
所成的角为60°,直线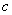 ⊥
⊥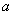 ,过空间任一点 P,作直线 a’∥a, b’∥b, c’∥c. 若a’,b’,c’ 共面则 b’ 与 c’ 成 30° 角,否则
,过空间任一点 P,作直线 a’∥a, b’∥b, c’∥c. 若a’,b’,c’ 共面则 b’ 与 c’ 成 30° 角,否则 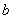 ’ 与
’ 与 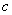 ’ 所成的角的范围为(30°,90°],所以直线b与c所成角的范围为[30°,90°] .
’ 所成的角的范围为(30°,90°],所以直线b与c所成角的范围为[30°,90°] .
二、填空题
11.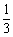
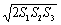 .解析:设三条侧棱长为 a,b,c.
.解析:设三条侧棱长为 a,b,c.
则 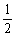 ab=S1,
ab=S1,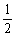 bc=S2,
bc=S2,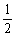 ca=S3 三式相乘:
ca=S3 三式相乘:
∴ 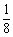 a2 b2 c2=S1S2S3,
a2 b2 c2=S1S2S3,
∴ abc=2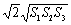 .
.
∵ 三侧棱两两垂直,
∴ V=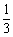 abc·
abc·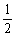 =
=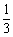
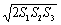 .
.
12.外,垂,内,中,BC边的垂直平分.
解析:(1)由三角形全等可证得 O 为△ABC 的外心;
(2)由直线和平面垂直的判定定理可证得,O 为△ABC 的垂心;
(3)由直线和平面垂直的判定定理可证得,O 为△ABC 的内心;
(4)由三角形全等可证得,O 为 AB 边的中点;
(5)由(1)知,O 在 BC 边的垂直平分线上,或说 O 在∠BAC 的平分线上.
13.60°.解析:将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为60°.
14.[30°,90°].解析:直线l与平面???所成的30°的角为m与l所成角的最小值,当m在???内适当旋转就可以得到l⊥m,即m与l所成角的的最大值为90°.
15.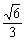 .解析:作等积变换:
.解析:作等积变换: ×(d1+d2+d3+d4)=
×(d1+d2+d3+d4)= ·h,而h=
·h,而h=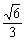 .
.
16.60°或120°.解析:不妨固定AB,则AC有两种可能.
 三、解答题
三、解答题
17.证明:(1)取BC中点O,连结AO,DO.
∵△ABC,△BCD都是边长为4的正三角形,
∴AO⊥BC,DO⊥BC,且AO∩DO=O,
∴BC⊥平面AOD.又AD 平面AOD,
平面AOD,
∴BC⊥AD. (第17题)
解:(2)由(1)知∠AOD为二面角A-BC-D的平面角,设∠AOD=?,则过点D作DE⊥AD,垂足为E.
∵BC⊥平面ADO,且BC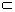 平面ABC,
平面ABC,
∴平面ADO⊥平面ABC.又平面ADO∩平面ABC=AO,
∴DE⊥平面ABC.
∴线段DE的长为点D到平面ABC的距离,即DE=3.
又DO=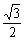 BD=2
BD=2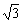 ,
,
在Rt△DEO中,sin?=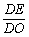 =
=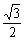 ,
,
故二面角A-BC-D的正弦值为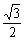 .
.
(3)当 ?=90°时,四面体ABCD的体积最大.
18.证明:(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.∴ ,即DE⊥EC.
,即DE⊥EC.
在长方体ABCD- 中,BC⊥平面
中,BC⊥平面 ,又DE
,又DE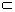 平面
平面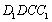 ,
,
∴BC⊥DE.又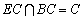 ,∴DE⊥平面EBC.∵平面DEB过DE,∴平面DEB⊥平面EBC.
,∴DE⊥平面EBC.∵平面DEB过DE,∴平面DEB⊥平面EBC.
 (2)解:如图,过E在平面
(2)解:如图,过E在平面 中作EO⊥DC于O.在长方体ABCD-
中作EO⊥DC于O.在长方体ABCD-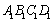 中,∵面ABCD⊥面
中,∵面ABCD⊥面 ,∴EO⊥面ABCD.过O在平面DBC中作OF⊥DB于F,连结EF,∴EF⊥BD.∠EFO为二面角E-DB-C的平面角.利用平面几何知识可得OF=
,∴EO⊥面ABCD.过O在平面DBC中作OF⊥DB于F,连结EF,∴EF⊥BD.∠EFO为二面角E-DB-C的平面角.利用平面几何知识可得OF=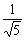 , (第18题)
, (第18题)
又OE=1,所以,tan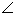 EFO=
EFO=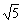 .
.
19*.解:(1)直角梯形ABCD的面积是M底面=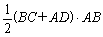 =
=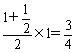 ,
,
∴四棱锥S—ABCD的体积是V=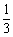 ·SA·M底面=
·SA·M底面=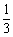 ×1×
×1× =
=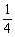 .
.
(2)如图,延长BA,CD相交于点E,连结SE,则SE是所求二面角的棱.
∵AD∥BC,BC=2AD,
∴EA=AB=SA,∴SE⊥SB
∵SA⊥面ABCD,得面SEB⊥面EBC,EB是交线.
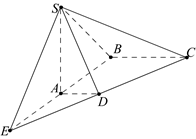 又BC⊥EB,∴BC⊥面SEB,故SB是SC在面SEB
又BC⊥EB,∴BC⊥面SEB,故SB是SC在面SEB
上的射影,
∴CS⊥SE,∠BSC是所求二面角的平面角.
∵SB=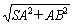 =
=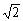 ,BC=1,BC⊥SB,
,BC=1,BC⊥SB,
∴tan∠BSC=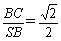 , (第19题)
, (第19题)
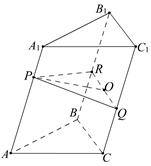 即所求二面角的正切值为
即所求二面角的正切值为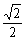 .
.
 20*.解:如图,设斜三棱柱
ABC—
A
1
B
1
C
1的侧面
BB
1
C
1
C的面积为10,
A
1
A和面
BB
1
C
1
C的距离为6,在
AA
1上取一点
P作截面
PQR,使
AA
1⊥截面
PQR,
AA
1∥CC
1,∴截面
PQR⊥侧面
BB
1
C
1
C,过
P作
PO⊥
QR于
O,则
PO⊥侧面
BB
1
C
1
C,且
PO=6.
20*.解:如图,设斜三棱柱
ABC—
A
1
B
1
C
1的侧面
BB
1
C
1
C的面积为10,
A
1
A和面
BB
1
C
1
C的距离为6,在
AA
1上取一点
P作截面
PQR,使
AA
1⊥截面
PQR,
AA
1∥CC
1,∴截面
PQR⊥侧面
BB
1
C
1
C,过
P作
PO⊥
QR于
O,则
PO⊥侧面
BB
1
C
1
C,且
PO=6.
∴V斜=S△PQR·AA1= ·QR·PO·AA1
·QR·PO·AA1
= ·PO·QR·BB1
·PO·QR·BB1
= ×10×6
×10×6
=30.
-
高中数学必修2第二章知识点+习题+答案
第二章直线与平面的位置关系21空间点直线平面之间的位置关系2111平面含义平面是无限延展的2平面的画法及表示1平面的画法水平放置的…
-
高一数学必修2知识点总结
高中数学必修2知识点一直线与方程1直线的倾斜角定义x轴正向与直线向上方向之间所成的角叫直线的倾斜角特别地当直线与x轴平行或重合时我…
-
高中数学必修2知识点总结:第二章 直线与平面的位置关系
归海木心QQ634102564高中数学必修2知识点总结第二章直线与平面的位置关系21空间点直线平面之间的位置关系2111平面含义平…
-
高中数学必修2知识点总结
高中数学必修2知识点总结第一章空间几何体一空间几何体的结构及表面积和体积1柱体V柱S底h1棱柱2圆柱S侧2rhr为底面圆的半径h为…
-
20xx年高一数学必修二各章知识点总结
数学必修2知识点1多面体的面积和体积公式表中S表示面积cc分别表示上下底面周长h表示高h表示斜高l表示侧棱长2旋转体的面积和体积公…
-
导数及其应用概念及公式总结
导数与微积分重要概念及公式总结1.平均变化率:?yf(x2)?f(x1)?称为函数f(x)从x1到x2的平均变化率?xx2?x12…
-
考研数学:高数重要公式总结(中值定理与导数应用)
凯程考研集训营为学生引路为学员服务考研数学高数重要公式总结中值定理与导数应用考研数学中公式的理解记忆是最基础的其次才能针对具体题型…
-
导数和高阶导数公式总结
基本导数公式c0axaxlnaxxeesinxcosx2tanxseccsc2xcotxxsecxsecxtanxcscx1arc…
-
考研数学:高数重要公式总结(导数公式)
凯程考研历史悠久专注考研科学应试严格管理成就学员考研数学高数重要公式总结导数公式考研数学中公式的理解记忆是最基础的其次才能针对具体…
-
考研数学:高数重要公式总结(导数公式)
凯程考研集训营为学生引路为学员服务考研数学高数重要公式总结导数公式考研数学中公式的理解记忆是最基础的其次才能针对具体题型进行基础知…
-
无线通信知识总结
1.通信技术的发展主要经历了三个阶段。(1)初级通信阶段(以18xx年电报发明为标志)年代历史事件18xx年莫尔斯发明有线电报,开…