导数总结
概念、方法、题型、易误点及应试技巧总结
基本概念、公式及方法是数学解题的基础工具和基本技能,为此作为高三学生,务必首先要掌握高中数学中的概念、公式及基本解题方法,其次要熟悉一些基本题型,明确解题的易误点,还应了解一些常用结论,最后还要掌握一些的应试技巧。本资料对高中数学所涉及到的概念、公式、常见题型、常用方法和结论及解题中的易误点,按章节进行了系统的整理,最后阐述了考试中的一些常用技巧,相信通过对本资料的认真研读,一定能大幅度提升高考数学成绩。
四、导数与微积分
1、导数定义:记作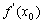 或
或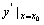 ,即
,即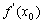 =
=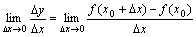 .
.
注:函数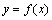 在点
在点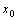 处连续是
处连续是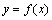 在点
在点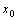 处可导的必要不充分条件.
处可导的必要不充分条件.
2、常用函数的导数公式:①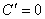 这里
这里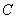 是常数。即常数的导数值为0。
是常数。即常数的导数值为0。
② 特别地:
特别地: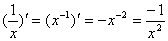
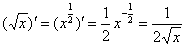
③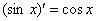 ④
④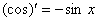 ⑤
⑤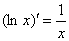 ⑥
⑥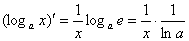 ⑦
⑦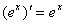 ⑧
⑧ 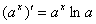
3、求导数的四则运算法则及复合函数的求导法则

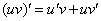

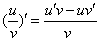
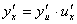
4、导数的意义:①几何意义: 表示经过曲线
表示经过曲线 上的切点
上的切点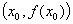 的切线的斜率。②物理意义:
的切线的斜率。②物理意义: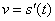 表示即时速度。
表示即时速度。 表示加速度。
表示加速度。
5、导数的应用:1)、求切线的方程:①已知切点时求切线的步骤:求出函数 在点
在点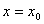 的导数,即曲线
的导数,即曲线 在切点
在切点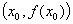 的切线的斜率;再利用点斜式方程为:
的切线的斜率;再利用点斜式方程为: 的可得切线的方程。②若未知切点,根据需要,可先设切点坐标为
的可得切线的方程。②若未知切点,根据需要,可先设切点坐标为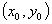 ,再根据具体问题用待定系数法求解。例:求过点
,再根据具体问题用待定系数法求解。例:求过点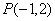 且与曲线
且与曲线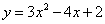 在点
在点 处的切线平行的直线方程
处的切线平行的直线方程
2)、导数与函数的单调性的关系:① 在区间
在区间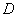 上恒成立
上恒成立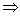
 区间
区间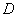 上为增函数;②
上为增函数;② 区间
区间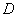 上为增函数
上为增函数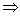
 区间
区间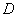 上恒在成立
上恒在成立
单调区间的求解过程:已知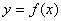 ,先分析
,先分析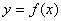 的定义域;再求导数
的定义域;再求导数 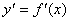 ;最后解不等式
;最后解不等式 ,解集在定义域内的部分为增区间(解不等式
,解集在定义域内的部分为增区间(解不等式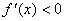 ,解集在定义域内的部分为减区间)。
,解集在定义域内的部分为减区间)。
例:设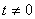 ,点
,点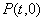 是函数
是函数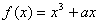 与
与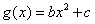 的图象的一个公共点,两函数的图象在
的图象的一个公共点,两函数的图象在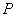 处有相同的切线,(1)用
处有相同的切线,(1)用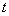 表示
表示 、
、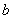 、
、 ; (2)若函数
; (2)若函数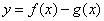 在
在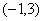 上单调递减,求
上单调递减,求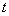 的取值范围。
的取值范围。
3)、求极值、求最值。
① 注意:极值≠最值。函数 在区间
在区间 上的最大值是
上的最大值是 、
、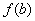 和极大值中最大的一个。最小值是
和极大值中最大的一个。最小值是 、
、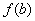 和极小值中最小的一个。
和极小值中最小的一个。
② 由 还不能得到确定当
还不能得到确定当 为
为 极值点,还需结合函数的单调性才能作出判断。如
极值点,还需结合函数的单调性才能作出判断。如 不是
不是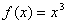 的极值点;
的极值点;
③ 极值点的可能除了使 外,还有可能在不可导点处,如
外,还有可能在不可导点处,如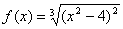
④ 若 为
为 极值点则可到
极值点则可到
⑤ 已知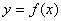 ,求函数
,求函数 极值的步骤:先求导数
极值的步骤:先求导数 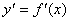 ;再由方程
;再由方程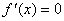 求出得可疑点(还应包括不可导点);最后检查
求出得可疑点(还应包括不可导点);最后检查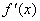 在可疑点处左右的值的符号,从而确函数
在可疑点处左右的值的符号,从而确函数 的在方程根左右的区间的单调性,如果左增右减,那么
的在方程根左右的区间的单调性,如果左增右减,那么 在这个可疑点处取得极大值,如果左减右增,那么
在这个可疑点处取得极大值,如果左减右增,那么 在这个可疑点处取得极小值。
在这个可疑点处取得极小值。
例:已知函数 (
(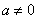 )是
)是 上的奇函数,当
上的奇函数,当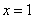 时,
时, 取得极值-2,
取得极值-2,
(1)求 的单调区间和极大值; (2)证明:对任意
的单调区间和极大值; (2)证明:对任意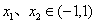 ,不等式
,不等式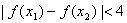 恒成立。
恒成立。
4、利用导数证明不等式
例:已知 ,求证:
,求证:
5、刻画函数(比初等方法精确细微)可与方程结合起来
例:已知函数 ,试证明方程
,试证明方程 在区间
在区间 内有且仅有一根
内有且仅有一根
例:已知函数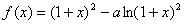 在区间
在区间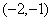 上是增函数,在区间
上是增函数,在区间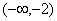 上为减函数
上为减函数
(1) 求 的表达式;
的表达式;
(2)若当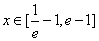 时,求使不等式
时,求使不等式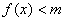 恒成立的最小自然数
恒成立的最小自然数
(3)是否存在实数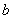 使得关于
使得关于 的方程
的方程 在区间
在区间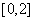 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数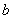 的取值范围
的取值范围
6、导数与解析几何或函数图象的混合问题是一种重要类型,也是高考中考察综合能力的一个方向。
五、定积分
1、曲边梯形的面积:
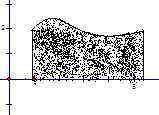 1)、设曲边梯形是由连续曲线
1)、设曲边梯形是由连续曲线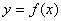 、
、 轴,与直线
轴,与直线 、
、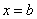 所围成,如图,计算时可分为四个步骤:分割、近似代替、求和、取极限。
所围成,如图,计算时可分为四个步骤:分割、近似代替、求和、取极限。
2)、定积分如果函数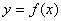 在区间
在区间 上连续,用分点
上连续,用分点 将区间等分为个
将区间等分为个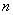 小区间,在每个小区间
小区间,在每个小区间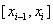 上任取一点
上任取一点 (
(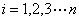 ),作和式
),作和式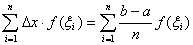 ,当
,当 时,上述和式无限趋近于某个常数,这个常数叫做函数
时,上述和式无限趋近于某个常数,这个常数叫做函数 在区间上的
在区间上的 定积分,记作
定积分,记作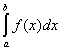 ,即
,即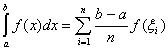
① 积分值仅与被积函数及积分区间有关,而与积分变量的字母无关。即
② 定义中区间的分法和的取法都是任意的。
③ 在定积分的定义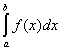 中,限定下限小于限,即
中,限定下限小于限,即 ,为了方便计算,可以把定积分的概念扩大,使下限不一定小于上限,并规定:
,为了方便计算,可以把定积分的概念扩大,使下限不一定小于上限,并规定: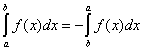 、
、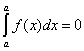
2、定积分的性质:
①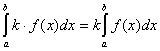
②
③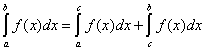 (
(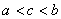 )
)
3、定积分的几何意义:在区间 上,若
上,若 既可取正值又可取负值时,曲线
既可取正值又可取负值时,曲线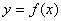 的某些部分在
的某些部分在 轴上方,而其他部分在
轴上方,而其他部分在 轴下方,如果我们将在
轴下方,如果我们将在 轴上方的面积赋予正值,在
轴上方的面积赋予正值,在 轴上方的面积赋予负值,那么在一般情形下,定积分
轴上方的面积赋予负值,那么在一般情形下,定积分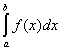 的几何意义是曲线
的几何意义是曲线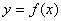 以及直线
以及直线 、
、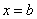 与
与 轴所围成的曲边梯形的面积的代数和;
轴所围成的曲边梯形的面积的代数和;
例:计算下列定积分:(1) (2)
(2)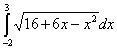
4、微积分基本定理(牛顿-莱布尼兹公式):
一般地,如果 是区间上的
是区间上的 的连续函数并且函数
的连续函数并且函数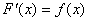 ,那么:
,那么: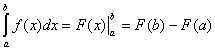 。
。
5、基本积分公式:
① ②
②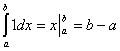 ③
③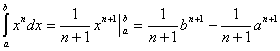
④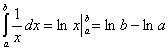 ⑤
⑤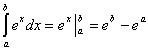 ⑥
⑥ ⑦
⑦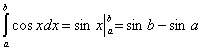
6、定积的应用:
① 平面图形的面积:如果平面图形由连续曲线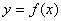 、
、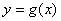 ,与直线
,与直线 、
、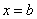 所围成,那么这块图形的面积为:
所围成,那么这块图形的面积为: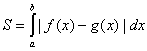
② 由曲线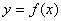 以及两条直线
以及两条直线 、
、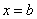 和
和 轴所围成的曲边梯形绕
轴所围成的曲边梯形绕 轴旋转一周面成的旋转体的体积分式为:
轴旋转一周面成的旋转体的体积分式为:
③ 变速直线运动的路程:作变速直线运动物体所经过的路程 等于其速度函数
等于其速度函数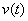 (
(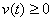 )在时间区间
)在时间区间 上的定积分,即:
上的定积分,即: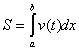
④ 变力作功:一物体沿变力 相同方向从
相同方向从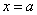 移动到
移动到 时,变力所作的功为:
时,变力所作的功为: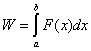 。
。
第二篇:导数总结
导数专题
一.本章知识结构
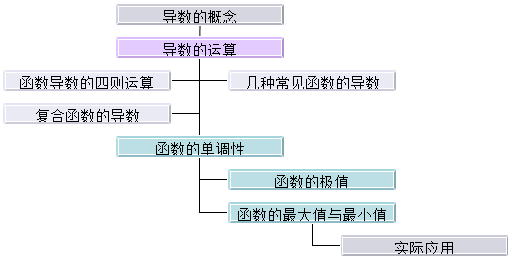
二.本章知识总结
(1)导数的概念:
1.导数的定义:对函数y=f(x),在点x=x0处给自变量x以增量 x,函数y相应有增量
x,函数y相应有增量 y=f(x0+
y=f(x0+ x)-f(x0),若极限
x)-f(x0),若极限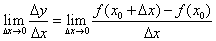 存在,则此极限称为f(x)在点x=x0处的导数,记为f ’(x0),或y’|
存在,则此极限称为f(x)在点x=x0处的导数,记为f ’(x0),或y’| ;
;
2.导函数:如果函数y=f(x)在区间(a,b)内每一点都可导,就说y=f(x)在区间(a,b)内可导.即对于开区间(a,b)内每一个确定的x0值,都相对应着一个确定的导数f ’(x0),这样在开区间(a,b)内构成一个新函数,把这一新函数叫做f(x)在(a,b)内的导函数.简称导数.记作f ’(x)或y’.
即f ’(x)=y’=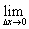
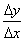 =
=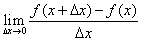 。
。
3.导数的几何意义:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在P(x0,f(x0))处的切线的斜率,即曲线y=f(x)在点P(x0,f(x0))处的切线斜率为k=f ’(x0).函数 y=f(x)在点 P(x0,f(x0))处的切线方程为 y-y0=f ’(x0)·(x-x0).函数y=f(x)在点P(x0,f(x0))处的法线方程为y-y0=-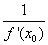 (x-x0)或x=x0.
(x-x0)或x=x0.
(2)常见函数的导数:
(c)’=0, (c为常数);(xm)’=mx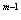 ;(sinx)’=cosx;
;(sinx)’=cosx;
(cosx)’=-sinx;(ex)’=ex;(ax)’=ax·lna;(lnx)’= ;(ligax)’=
;(ligax)’= .
.
(3)导数的运算:
1.函数的和或差的导数
法则:两个函数的和或差的导数,等于两个函数的导数的和或差,即(u±v)’=u’±v’.
2.函数的积的导教
法则:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数,即 (uv)’=u’v+v’u.
3.函数的商的导
法则:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方.即(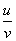 )’=
)’=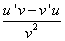 (v≠0)。
(v≠0)。
4.复合函数的导数
法则:设函数u=g(x)在点x处有导数u’x=g’(x),函数f(u)在点x处的u处有导数y’u=f ’(u);则复合函数y=f[(x)]在点x处也有导数,且 y’x=y’u·u’x,也可简述为:复合函数对自变量的导数,等于已知函数对中间变量的导数乘以中间变量对自变量的导数。
(4)函数的单调性
设函数y=f(x)在某个区间内可导,如果f ’( x)>0时,则函数y=f( x)为增函数;如果f ’(x)<0时,则函数y=f(x)为减函数;如果恒有f ’( x)=0,则y=f(x)为常函数.
(5)函数的极值
1.设函数y=f(x)在x0附近有定义,如果对x0附近的所有点x都有f(x)<f(x0),则称f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0);
2.如果对x0附近的所有点x,都有f(x)>f(x0)称f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),极大值与极小值统称为极值。
3.判断法则:
① 对于在x0处连续的函数,如果在x0附近的左侧f ’(x)>0,右侧f ’(x)<0,那么f(x0)是极大值;
② 如果在x0附近的左侧f ’(x)<0,右侧f ’(x)>0,那么f(x0)是极小值.
(6)函数的最大值与最小值
1.定义:最值是一个整体性概念,是指函数在给定区向(或定义域)内所有函数值中最大的值或最小的值,最大数值叫最大值,最小的值叫最小值,通常最大值记为M,最小值记为m.
2.存在性:在闭区间[a,b]上连续函数f(x)在[a,b]上必有最大值与最小值.
3.求最大(小)值的方法:函数f(x)在闭区间[a,b]上最值求法:
① 求出f(x)在(a,b)内的极值;
② 将函数f(x)的极值与f(a),f(b)比较,其中较大的一个是最大值,较小的一个是最小值.
三.学习方法与指导
(一)学习方法点拨
1.导数的概念:
设f(x)在点x=x0 附近有定义,若极限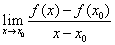 存在,则称其为f(x)在点x=x0处的导数f ’(x0).可以证明这一结论与教科书上的导数定义是等价的.
存在,则称其为f(x)在点x=x0处的导数f ’(x0).可以证明这一结论与教科书上的导数定义是等价的.
另外,若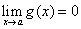 ,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠0,则
,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠0,则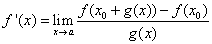 ,又若
,又若 ,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠x0,则
,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠x0,则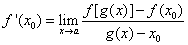 .
.
设f(x)=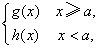 那么g(a)=h(a)=A,且
那么g(a)=h(a)=A,且
为f(x)在点x=a处可导的充要条件,此时f ’(a)=B.
由此可知,若分段函数f(x)的表达式中的g(x)、h(x)可分别看做含有a的区间(α,β)上的函数,且g(a)=h(a),g’(a)=h’(a),则f(x)在点x=a处可导;且有f ’(a)==g’(a)=h’(a).
2.曲线的切线:
设曲线S:y=f(x),若f ’(x0)存在,则S在点P(x0,f(x0)处的切线方程为
l:y-f(x0)=f’(x0)(x-x0).
可见l的方程被x0所唯一确定;若f(x)在区间(α,β)内可导,则当点x0在(α,β)内变动时,点P(x0,f(x0))在S上变动,而l“贴着”曲线S转动.所以要求具有某种性质的切线,可转化为这种性质对点x0的要求,解出x0,即可求出对应的切线方程.
应当了解可能一曲线在某点处不可导;但在这一点的切线还是存在的,例如曲线y= 在点x=0处不可导,但在原点处有切线x=0.
在点x=0处不可导,但在原点处有切线x=0.
3.导数运算
要熟练掌握基本导数公式以及函数的和、差、积、商的求导法则.
对复合函数求导法则,应首先搞清楚函数的复合过程,方法是研究运算顺序,例如给定函数y=ln(sinex),所谓运算顺序是指对自变量x,应先计算u=ex,再计算v=sinu,最后算出y=lnv,然后倒过来即得复合过程y=lnv,v=sinu,u=ex,从而有y’= .
.
对复合函数求导法则的掌握,要熟练到可以不写出复合过程而直接写出求导结果.
4.函数的单调性
应当理解函数的单调性与可导性并无本质的联系,甚至具有单调性的函数并不一定连续.我们只是利用可导来研究单调性,这样就将研究的范围局限于可导函数.
f(x)在区间I上可导,那么f ’(x)> 0是f(x)为增函数的充分条件,例如f(x)=x3是定义于R的增函数,但f ’(0)=0,这说明f ’(x)>0非必要条件.
我们也可利用导数来证明一些不等式.如f(x)、g(x)均在[a、b]上连续,(a,b)上可导,那么令h(x)=f(x)-g(x),则h(x)也在[a,b]上连续,且在(a,b)上可导,若对任何x∈(a,b)有 h’(x)>0且 h(a)≥0,则当x∈(a,b)时 h(x)>h(a)=0,从而f(x)>g(x)对所有x∈(a,b)成立.
5.可导函数的极值
从函数的极值定义看,极值的存在与可微性无必然联系.如f(x)=|x-1|,易见当x=1时f(x)取得极小值,但f ’(1)不存在.所以用研究导数的方法探求函数的极值,实际上是将研究的范围局限于可导函数.
对可导函数f(x),在x=x0取极值的必要条件是f(x0)=0.又设f(x)在点x=x0处取得极小值,是否一定存在x0的邻域(α,β),使当x∈(α,x0)时f ’(x)<0,且当x∈(x0,β)时f ’(x)>0,答案是否定的,即f ’(x)在x0的“左侧附近”为负,且在x0“右侧附近”为正仅是f(x0)为极小值的充分条件,为说明这一情况,我们考察函数f(x)= ,由于
,由于 ,故有
,故有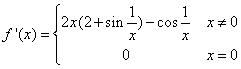 ,
,
即f(x)在R上可导.又当x≠0时f(x)>0,而f(0)=0,故当x=0时f(x)取得极小值0,但对任何α<0,总可取到充分小的 k∈Z,使 x1=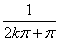 ∈(α,0),且f ’(x1)=
∈(α,0),且f ’(x1)= >0,又对任何β>0,总可取到充分大的k∈Z,使x2=
>0,又对任何β>0,总可取到充分大的k∈Z,使x2=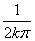 ∈(0,β),且f ’(x2)=
∈(0,β),且f ’(x2)=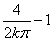 <0.
<0.
6.函数的最大值与最小值
函数的极值是“局部性质”,例如极小值点是指存在一个邻域,在其中此点的函数值最小,而函数的最大值、最小值是“全局性质”,即在函数的整体定义域内的某点处函数值最大(小),这两个概念是有区别的.但它们也有联系,即当最大(小)值点在区间内部时,它当然也是极值点,所以求定义于区间[a,b]上的函数f(x)的最大(小)值时,只需此较诸极值与区间端点处的函数值f(x)、f(b)即可.
我们知道,[a,b]上的连续函数 f(x)必有最大值与最小值.若又有 f(x)在(a, b)上可导的条件,则由极值点处f ’(x)=0可知最大(小)值点 x0∈{x| f ’(x0)=0或x=a或x=b}.但由于f(x)在[a,b]上连续并不能保证其在(a,b)内可导,而最大(小)值可能出现在f ’(x)不存在的点处(如f(x)=|x(x-1)|,易见最小值为0,出现在点x=0或x=1处,而此时f ’(x)不存在),所以若仅有f(x)在[a,b]连续的条件,为求f(x)的最大(小)值,还需要求出使f ’(x)不存在的点,将这些点处的函数值与诸极值及f(a)、f(b)比较,从而确定最大值与最小值.
根据上述分析,若f(x)在[a,b]上连续,在(a,b)内可导,如果我们可从另外的途径,比如问题的实际背景判断出f(x)的最小值不可能出现在点x=a、x=b处,那么当方程f ’(x)=0在(a,b)内仅有一解x0时,则可断定f(x0)为最小值.
-
20xx一模导数总结题
东城示范(一模理)18.(13分)已知函数:f(x)?x?(a?1)lnx?a1(a?R),g(x)?x2?ex?xexx2(1)…
-
导数总结
总结基本初等函数的导数公式:1、(tanx)’=sec2x2、(secx)’=secx*tanx3、(cotx)’=-csc2x4…
-
导数总结
概念、方法、题型、易误点及应试技巧总结基本概念、公式及方法是数学解题的基础工具和基本技能,为此作为高三学生,务必首先要掌握高中数学…
-
导数题型归纳总结
导数题型归纳总结函数fx在x0处的导数fx0limx0fx0xfx0ylimxx0x函数yfx在点x0处的导数的几何意义是在该点处…
-
《导数及其应用》知识点总结
一、导数的概念和几何意义1.函数的平均变化率:函数f(x)在区间[x1,x2]上的平均变化率为:f(x2)?f(x1)。x2?x1…
-
20xx一模导数总结题
东城示范(一模理)18.(13分)已知函数:f(x)?x?(a?1)lnx?a1(a?R),g(x)?x2?ex?xexx2(1)…
-
第二届变废为宝大赛总结报告
总结报告在20xx年新学期开始,我阿职院绿色环保协会为更好的丰富喔院学生的课余活动生活和宣传环保知识,与20xx年x月在学院举办了…
-
英语阅读技巧总结
阅读短文应遵循由整体到细节的原则,按“全文、段落、句子、词语”的步骤阅读文章。可采用通读、细读和复读的方法找到最佳答案。?一般的阅…
-
综合实践活动课——生活中的垃圾活动总结
综合实践活动课——“生活中的垃圾”活动总结——黄土梁子明德小学五年一班今天,我们班的综合实践活动——“生活中的垃圾”完成了成果展示…
-
学籍管理工作总结
20xx~20xx第一学期期末个人工作总结(学籍管理工作)学籍管理是教育行政部门和学校最基本的常规管理,它在全面推进素质教育深化主…