导数题型归纳总结

函数f(x)在x0处的导数：f?(x0)

=lim?x?0f(x0??x)?f(x0)?y=lim ?x?x?0?x

函数y=f（x）在点x0处的导数的几何意义是在该点处的切线的斜率即k?f?(x0) 求切线方程：先用导数求斜率，再用点斜式求出切线方程；切点既在直线上又在曲线上 注：(x1,y1)要先设切点(x0,f(x0))，用k=f?(x0)?y1?f(x0) x1?x0

21、若曲线y?x?ax?b在点(0,b)处的切线方程是x?y?1?0，则a?b?232、若存在过点(1,0)的直线与曲线y?x和y?ax?15x?9都相切，则a=4

3、已知y?x?2x，则过原点(0,0)的切线方程是 32

34、★已知f(x)?x?3x，过点A(1,m)(m??2)可作y?f(x)的三条切线，则m的范围是

，?1)的切线方程5、（曲线上一点）求过曲线y?x3?2x上的点(1 注：过曲线上一点的切线，该点未必是切点

6、【2012·辽宁】已知P,Q为抛物线x2=2y上两点，点P,Q的横坐标分别为4，?2，过P,Q分别作抛物线的切线，两切线交于点A，则点A的纵坐标为

(A) 1 (B) 3 (C) ?4 (D) ?

8

y??0单调递增；y??0单调递减 极值问题：左升右降有极大值；左降右升有极小值；极值点的左右两侧f?(x)的符号相反； f?(x)=0的点不一定是极值点，但极值点一定满足f?(x)=0；

求函数极值的步骤：①确定函数的定义域；②求导数，令f?(x)=0，找出所有的驻点；③ 检查驻点左右的符号，左正右负有极大值，左负右正有极小值；

函数f(x)在?a,b?上连续，则f(x)在极值点或端点处取得最值 1、函数f(x)?(x?3)e的单调递增区间是 x ( )

A. (??,2) B.(0,3) C.(1,4) D. (2,??)

2、要使函数f(x)?x2?3(a?1)x?2在区间(??,3]上是减函数，求实数a的取值范围。

2f(x)?lnx?a(1?a)x?2(1?a)x的单调性 a?03、【2011·广东】设,讨论函数

4、【2012·辽宁】函数y=

A．(?1,1]

12x?㏑x的单调递减区间为 （ ） 2B．(0,1] C．[1,+∞) D．(0,+∞)

基础题：1、求f?x??13x?4x?4在?0,3? 3

综合题1、设函数f(x)?x3?ax2?a2x?m (a?0)

（I）若a?1时函数f(x)有三个互不相同的零点，求m的范围；

（II）若函数f(x)在??1,1?内没有极值点，求a的范围；

（III）若对任意的a??3,6?，不等式f(x)?1在x???2,2?上恒成立，求实数m的取值范围.

2、设函数f(x)??13x?2ax2?3a2x?b，(0?a?1,b?R) 3

4若当x??a?1,a?2?时，恒有f?(x)?a，试确定a≤a<1） 5

323、【2009·浙江】已知函数f(x)?x?(1?a)x?a(a?2)x?b (a,b?R)．

（I）若函数f(x)的图象过原点，且在原点处的切线斜率是?3，求a,b的值； （II）若函数f(x)在区间(?1,1)上不单调，求a的取值范围． ．．．

4、已知函数f(x)=ax?

若在区间??

5、【2011·湖北】设函数f，gx，其中x?R，a、b()x?x?2ax?bx?a()?x?3x?2

为常数，已知曲线y?f(x)与y?g(x)在点（2,0）处有相同的切线l。

(I) 求a、b的值，并写出切线l的方程；

(II)若方程f()有三个互不相同的实根0、x、x，其中x1?x2，且对任意的x?g()x?mx322332x?1(x?R)，其中a?0. 2?11?,?上，f(x)?0恒成立，求a的取值范围.（ a的取值范围为0<a<5） 22??

x??x恒成立，求实数m的取值范围。 ()?g()x?m(x?1)1,x2?，fx

326、已知函数f(x)?x?ax?x?1，a?R．设函数f(x)在区间??，??内是减函数，?2

?31?3?

求a的取值范围．（a≥

7） 4

1、当x?0，求证：e?1?x（(ex)??ex） x

2、设函数f(x)?x?(x?1)ln(x?1)(x??1).

（Ⅰ）求f(x)的单调区间；（Ⅱ）证明：当n?m?0时，(1?n)m?(1?m)n

本类问题主要是命题人经常考查的一类如nam?b（m?n），一般两边同时取自然对数，mlna?nlnb，再利用函数单调性，可能还需要构造函数

函数图像

1、【2012·重庆】设函数f(x)在R上可导,其导函数f?(x),且函数f(x)在x??2处取得极小

值,则函数y?xf?(x)的图象可能是

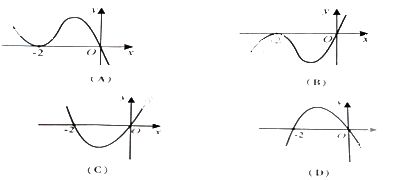
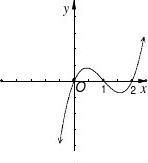
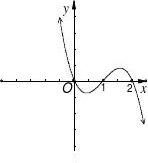
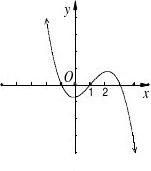
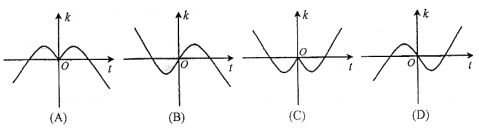
2、设函数f?x??xsinx?cosx的图像在点t,f?t?处切线的斜率为k，则函数k?g?t?的

部分图像为( ) ??

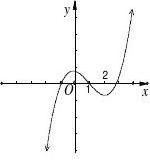
3、y?f?(x )是f(x)的导函数，y?f?(x)的图象如下图所示，则y?f(x)的图象为（ ）

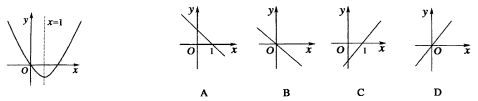
4、已知二次函数f(x)的图象如下图所示，则其导函数f′(x)的图象的大致形状是（ ）

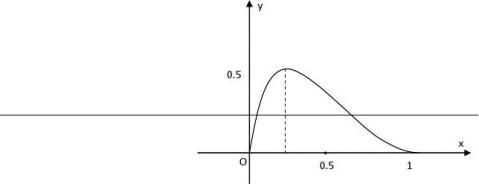
5、【2011·安徽】函数f(x)?axg(??x)在区间〔0,1〕上的图像如图所示，则m，n的值可能是 ( )

（A）m?1,n?1 (B) m?1,n?2

(C) m?2,n?1 (D) m?3,n?1

mn

综合问题

21、【2012·黄冈中学高二期中】设函数f． (x)(?1??x)2ln(1?x)

（I）求f(x)的单调区间；

2（II）当0<a<2时，求函数g在区间[0，3]上的最小值． (x)?f(xxa)??x?1

2、【2011·北京】已知点A?0,2?,B?2,0?,若点C在函数y?x的图象上，则使得?ABC的面2

积为2的点C的个数为 （ ）

A. 4 B. 3 C. 2 D. 1

3、【2012·福建】已知f(x)?x3?6x2?9x?abc,a?b?c,且f(a)?f(b)?f(c)?0.现给

出如下结论:①f(0)f(1)?0;②f(0)f(1)?0;③f(0)f(3)?0;④f(0)f(3)?0.

其中正确结论的序号是

A．①③ B．①④

n4、【2012·湖北】设函数f(x)?ax(1?x)?b(x?0),n为正整数,a,b为常数,曲线y?f(x)在（ ） C．②③ D．②④

(1,f(1))处的切线方程为x?y?1.

(1)求a,b的值; (2)求函数f(x)的最大值; (3)证明:f(x)?

1. ne

5、【2012·江西】已知函数f(x)?(ax2?bx?c)ex在?0,1?上单调递减且满足

f(0)?1,f(0)?0.

(1)求a的取值范围;

(2)设g(x)?f(?x)?f?(x),求g(x)在?0,1?上的最大值和最小值.

6、设函数f(x)??13x?x2?(m2?1)x,(x?R,)其中m?0 3

已知函数f(x)有三个互不相同的零点0，x1,x2，且x1?x2，若对任意的

1x?[x1,x2]，f(x)?f(1)恒成立，求m的取值范围（m的取值范围是(,)） 23

17、已知函数f(x)＝ln(1＋x)－ax在x＝－1． 2

（Ⅰ）求a的值及f(x)的最大值；

111（Ⅱ）证明：1＋…＋＞ln(n＋1)（n∈N*） 23n

8、【2013·浙江教科院】设函数f (x)＝x3－4x＋a，0＜a＜2．若f (x)的三个零点为x1，x2，x3，

且x1＜x2＜x3，则 （ ）

A．x1＞－1 B．x2＜0 C．x2＞0 D．x3＞2

9、 已知m?R，函数f（x）＝mx?m?11?lnx，g(x)??lnx x2

（I）求g（x）的极小值；

（II）若y＝f (x)一g(x)在［1，＋?）上为单调增函数，求实数m的取值范围

 

第二篇：考前归纳总结：导数中的恒成立问题

导数中的恒成立问题

 一、常见基本题型：

     （1）已知某个不等式恒成立，去求参数的取值范围；

     （2）让你去证明某个不等式恒成立。

        解此类问题的指导思想是：构造函数，或参变量分离后构造函数，转化为求新函        数的最值问题。

例1：已知函数, 当时，不等式恒成立，      求实数的取值范围.

解：不等式可化为，

         即.

         记，要使上式成立，

         只须是增函数即可.

        即在[1,)上恒成立，

        即在上恒成立，故，

        所以实数的取值范围是（-，2] .

例2：已知，函数．

       （1）若函数在处的切线与直线平行，求的值；     

    （2）在（1）的条件下，若对任意，恒成立，求实数的取值组成的集合．

   解：（1），由已知，

        即，，解得或,

                  又因为，所以.

（2）当时，，由（2）知该函数在上单调递增，       因此在区间上的最小值只能在处取到. 

           又，

     若要保证对任意，恒成立，应该有，

         即，解得，

       因此实数的取值组成的集合是.

 例3. 函数，设，若，

  求证：对任意，且，都有.

 证明：因为，

   所以，

    因为，所以（当且仅当时等号成立），

      所以在区间上是增函数，     

    从而对任意，当时，，

     即,所以。

二、针对性练习

    1.已知函数在处取得极值，若对任意,不等   式恒成立, 求实数的取值范围．

 解：函数的定义域为  又，                 

     由题设在处取得极值，∴，即或。

         ∴。                            

      不等式恒成立，

          即 恒成立。                 

        又∴，当且仅当时，                      

       故时，不等式恒成立。

   2、设函数

   （Ⅰ）求函数的极值点；

   （Ⅱ）当p＞0时，若对任意的x＞0，恒有，求p的取值范围；

     解：（1），

                   

        当 上无极值点

        当p>0时，令的变化情况如下表：

        从上表可以看出：当p>0 时，有唯一的极大值点 

（Ⅱ）当p>0时在处取得极大值，此极大值也是最大值，

        要使恒成立，只需， 

               ∴。

 3.已知函数．

 （Ⅰ）求函数的单调区间；

 （Ⅱ）若函数的图像在点处的切线的倾斜角为，问：在什么范      围取值时，对于任意的，函数在区间上总存在      极值？

  解：（Ι）由知：

      当时，函数的单调增区间是，单调减区间是；

      当时，函数的单调增区间是，单调减区间是；

（Ⅱ）由,∴，.

           故，

     ∴,  ∵ 函数在区间上总存在极值，

          ∴有两个不等实根且至少有一个在区间内

         又∵函数是开口向上的二次函数，且，∴  

     由，∵在上单调递减，

        所以；∴，

      由， 解得；

综上得： 所以当在内取值时，对于任意的，函数   在区间上总存在极值。