向量分类总结
专题四:平面向量
【疑难点拨】
1.与向量概念有关的问题
⑴向量不同于数量,数量是只有大小的量(称标量),而向量既有大小又有方向;数量可以比较大小,而向量不能比较大小,只有它的模才能比较大小.记号“ >
> ”错了,而|
”错了,而| |>|
|>| |才有意义.
|才有意义.
⑵有些向量与起点有关,有些向量与起点无关.由于一切向量有其共性(力和方向),故我们只研究与起点无关的向量(既自由向量).当遇到与起点有关向量时,可平移向量.
⑶平行向量(既共线向量)不一定相等,但相等向量一定是平行向量,既向量平行是向量相等的必要条件.
⑷单位向量是模为1的向量,其坐标表示为( ),其中
),其中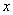 、
、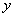 满足
满足 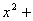
 =1(可用(cos
=1(可用(cos ,sin
,sin )(0≤
)(0≤ ≤2π)表示).求单位向量方法是向量本身除以自身的模;
≤2π)表示).求单位向量方法是向量本身除以自身的模;
⑸零向量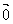 的长度为0,是有方向的,并且方向是任意的,实数0仅仅是一个无方向的实数.
的长度为0,是有方向的,并且方向是任意的,实数0仅仅是一个无方向的实数.
⑹有向线段是向量的一种表示方法,并不是说向量就是有向线段.
2.与向量运算有关的问题
⑴向量与向量相加,其和仍是一个向量.
①当两个向量 和
和 不共线时,
不共线时,
 的方向与
的方向与 、
、 都不相同,且|
都不相同,且|
 |<|
|<| |+|
|+| |;
|;
②当两个向量 和
和 共线且同向时,
共线且同向时,
 、
、 、
、 的方向都相同,且
的方向都相同,且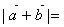
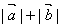 ;
;
③当向量 和
和 反向时,若|
反向时,若| |>|
|>| |,
|,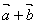 与
与 方向相同 ,且|
方向相同 ,且|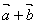 |=|
|=| |-|
|-| |;
|;
若| |<|
|<| |时,
|时,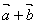 与
与 方向相同,且|
方向相同,且| +
+ |=|
|=| |-|
|-| |.
|.
⑵向量与向量相减,其差仍是一个向量.向量减法的实质是加法的逆运算.
⑶围成一周首尾相接的向量(有向线段表示)的和为零向量.
如,
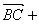
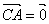 ,(在△ABC中)
,(在△ABC中)
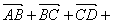
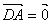 .(□ABCD中)
.(□ABCD中)
⑷判定两向量共线的注意事项
如果两个非零向量 ,
, ,使
,使 =λ
=λ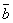 (λ∈R),那么
(λ∈R),那么 ∥
∥ ;
;
反之,如 ∥
∥ ,且
,且 ≠0,那么
≠0,那么 =λ
=λ .
.
这里在“反之”中,没有指出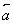 是非零向量,其原因为
是非零向量,其原因为 =0时,与λ
=0时,与λ 的方向规定为平行.
的方向规定为平行.
 =(x1,y1)
=(x1,y1) =(x2,y2), 那么
=(x2,y2), 那么 ∥
∥ 的充要条件是x1y2-x2y1=0 或者x1y2=x2y1
的充要条件是x1y2-x2y1=0 或者x1y2=x2y1
⑸数量积的8个重要性质
①两向量的夹角为0≤ ≤π.由于向量数量积的几何意义是一个向量的长度乘以另一向量在其上的射影值,其射影值可正、可负、可以为零,故向量的数量积是一个实数.
≤π.由于向量数量积的几何意义是一个向量的长度乘以另一向量在其上的射影值,其射影值可正、可负、可以为零,故向量的数量积是一个实数.
②设 、
、 都是非零向量,
都是非零向量, 是单位向量,
是单位向量, 是
是 与
与 的夹角,则
的夹角,则

③
 (∵
(∵ =90°,
=90°, 若
若 =(x1,y1)
=(x1,y1) =(x2,y2) 则
=(x2,y2) 则 x1x2+y1y2=0;
x1x2+y1y2=0;
④在实数运算中 =0
=0 =0或b=0.而在向量运算中
=0或b=0.而在向量运算中 =
=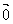
 =
=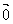 或
或 =
=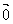 是错误的,故
是错误的,故 或
或 是
是 =0的充分而不必要条件.
=0的充分而不必要条件.
⑤当 与
与 同向时
同向时 =
= (
( =0,cos
=0,cos =1);
=1);
当 与
与 反向时,
反向时, =-
=- (
( =π,cos
=π,cos =-1),即
=-1),即 ∥
∥ 的另一个充要条件是
的另一个充要条件是 .
.
特殊情况有 =
= .
.
或 =
=
 =
= =
=
 .
.
如果表示向量 的有向线段的起点和终点的坐标分别为(
的有向线段的起点和终点的坐标分别为( ,
, ),(
),( ,
, ),则
),则 =
=
⑥ 。(因
。(因 )
)
⑦数量积不适合乘法结合律.
如 (因为
(因为 与
与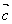 共线,而
共线,而 与
与 共线)
共线)
⑧数量积的消去律不成立.
若 、
、 、
、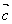 是非零向量且
是非零向量且 并不能得到
并不能得到 这是因为向量不能作除数,即
这是因为向量不能作除数,即 是无意义的.
是无意义的.
6.与平面向量基本定理及平移有关的问题
⑴平面向量基本定理是平面向量坐标表示的基础,它表明同一平面内的任一向量都可表示为其他两个不共线向量的线性组合.
⑵平面向量基本定理可联系物理学中力的分解模型进行理解。
⑶点的平移公式:
点 按给定平移向量
按给定平移向量 平移后得新点
平移后得新点 的坐标公式为
的坐标公式为

反之,由新点求旧点公式变为
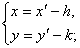
由新旧两点求平移向量公式为

⑷图象(图形)平移:
给定平移向量 =
=
 ,由旧解析式求新解析式,用公式
,由旧解析式求新解析式,用公式
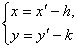
代入旧解析式中,整理得到;
由新解析式求旧解析式,用公式

代入新式,整理得到。
应用以上公式要注意公式中平移前的坐标 、平移后的坐标
、平移后的坐标 、平移向量坐标
、平移向量坐标 都在同一坐标系中。
都在同一坐标系中。
第二篇:向量总结
2.向量的概念
(1)向量的基本概念
①定义既有大小又有方向的量叫做向量。向量的大小也就是向量的长度,叫做向量的模。
②特定大小或特定关系的向量
零向量,单位向量,共线向量(平行向量),相等向量,相反向量。
③表示法:几何法:画有向线段表示,记为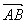 或α。
或α。
④在坐标系下,平面上任何一点都可用一对实数(坐标)来表示取x轴、y轴上两个单位向量 ,
, 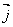 作基底,则平面内作一向量
作基底,则平面内作一向量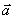 =x
=x +y
+y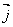 ,记作:
,记作: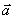 =(x, y) 称作向量
=(x, y) 称作向量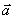 的坐标.
的坐标.
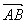 =(x2-x1,y2-y1),其中A(x1,y1),B(x2,y2)
=(x2-x1,y2-y1),其中A(x1,y1),B(x2,y2)
(2)向量的运算
①向量的加法与减法:定义与法则(如图5-1):
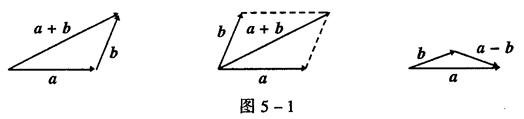
a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2)。其中a=(x1,y1),b=(x2,y2)。
运算律:a+b=b+a,(a+b)+c=a+(b+c),a+0=0+a=a。
 ②向量的数乘(实数与向量的积)定义与法则(如图5-2):
②向量的数乘(实数与向量的积)定义与法则(如图5-2):
λa=λ(x,y)=(λx, λy)
(1)︱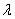
 ︱=︱
︱=︱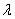 ︱·︱
︱·︱ ︱;
︱;
(2) 当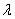 >0时,
>0时,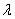
 与
与 的方向相同;当
的方向相同;当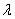 <0时,
<0时,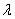
 与
与 的方向相反;
的方向相反;
当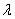 =0时,
=0时,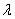
 =0.
=0.
(3)若 =(
=(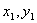 ),则
),则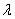 ·
· =(
=( ).
).
运算律
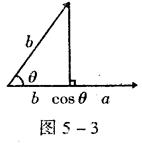 λ(μa)=(λμ)a,( λ+μ)a=λa+μa, λ(a+b)= λa+λb。
λ(μa)=(λμ)a,( λ+μ)a=λa+μa, λ(a+b)= λa+λb。
3.平面向量的数量积定义与法则(如图5-3):
(1).向量的夹角:已知两个非零向量 与b,作
与b,作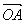 =
= ,
, 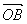 =
= ,则∠AOB=
,则∠AOB=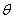 (
( )叫做向量
)叫做向量 与
与 的夹角。
的夹角。
(2).两个向量的数量积:
已知两个非零向量 与
与 ,它们的夹角为
,它们的夹角为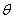 ,则
,则
 ·
· =︱
=︱ ︱·︱
︱·︱ ︱cos
︱cos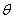 .
.
其中︱ ︱cos
︱cos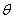 称为向量
称为向量 在
在 方向上的投影.
方向上的投影.
(3).向量的数量积的性质: ·
· =
= ·
· ,(λ
,(λ )·
)· =
= ·(λ
·(λ )=λ(
)=λ( ·
· ),(
),( +
+ )·
)·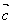 =
= ·
·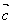 +
+ ·
·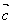 。若
。若 =(
=(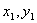 ),
), =(
=(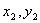 )则
)则 ·
· =
=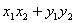
(ⅰ) ⊥
⊥
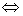
 ·
· =0
=0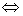
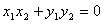 (
( ,
, 为非零向量);
为非零向量);
(ⅱ)向量 与
与 夹角为锐角
夹角为锐角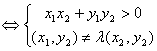
(ⅲ)向量 与
与 夹角为钝角
夹角为钝角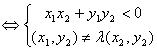
4.定理与公式
① 共线定理:向量b与非零向量a共线的充要条件是有且只有一个实数λ,使得b=λ a
结论: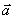 ∥
∥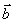 (
(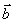 ¹
¹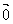 )的充要条件是x1y2-x2y1=0
)的充要条件是x1y2-x2y1=0
注意:1°消去λ时不能两式相除,∵y1, y2有可能为0, ∵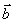 ¹
¹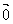 ∴x2, y2中至少有一个不为0
∴x2, y2中至少有一个不为0
2°充要条件不能写成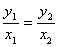 ∵x1, x2有可能为0
∵x1, x2有可能为0
3°向量共线的充要条件有两种形式: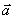 ∥
∥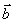 (
(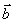 ¹
¹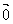 )
)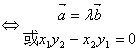
②平面向量基本定量:如果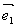 ,
,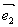 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数λ1,λ2使
,有且只有一对实数λ1,λ2使 =λ1
=λ1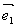 +λ2
+λ2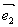
③两向量垂直的充要条件
(i)  ⊥
⊥
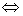
 ·
· =0 (ii)
=0 (ii)  ⊥
⊥
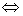 x1·x2+y1·y2=0(
x1·x2+y1·y2=0( =(x1,y1),
=(x1,y1),  =(x2,y2))
=(x2,y2))
④三点共线定理:平面上三点A、B、C共线的充要条件是:存在实数α、β,使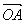 =α
=α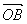 +β
+β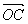 ,其中α+β=1,O为平面内的任一点。
,其中α+β=1,O为平面内的任一点。
⑤数值计算公式
两点间的距离公式:|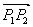 |=
|=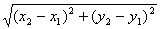 ,其中[P1(x1,y1),P2(x2,y2)]
,其中[P1(x1,y1),P2(x2,y2)]
P分有向线段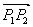 所成的比:
所成的比:
设P1、P2是直线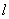 上两个点,点P是
上两个点,点P是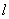 上不同于P1、P2的任意一点,则存在一个实数
上不同于P1、P2的任意一点,则存在一个实数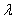 使
使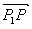 =
=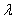
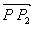 ,
,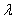 叫做点P分有向线段
叫做点P分有向线段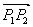 所成的比。
所成的比。
当点P在线段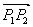 上时,
上时,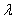 >0;当点P在线段
>0;当点P在线段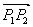 或
或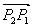 的延长线上时,
的延长线上时,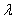 <0;
<0;
分点坐标公式:若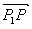 =
=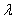
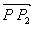 ;
;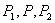 的坐标分别为(
的坐标分别为(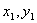 ),(
),(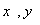 ),(
),(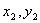 );则:
);则: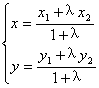 中点坐标公式:
中点坐标公式: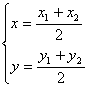
两向量的夹角公式:cosθ=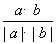 =
=
0≤θ≤180°,a=(x1,y1),b=(x2,y2)
⑥图形变换公式: 平移公式:若点P0(x,y)按向量a=(h,k)平移至P(x′,y′),
则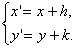
⑦有关结论
(i)平面内有任意三个点O,A,B。若M是线段AB的中点,则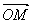

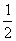 (
(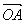 +
+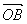 );
);
一般地,若P是分线段AB成定比λ的分点(即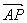 =λ
=λ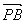 ,λ≠-1)则
,λ≠-1)则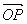 =
=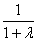
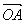 +
+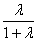
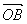 ,此即线段定比分点的向量式
,此即线段定比分点的向量式
(ii)有限个向量,a1,a2,…,an,相加,可以从点O出发,逐一作向量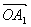 =a1,
=a1, 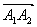 =a2,…,
=a2,…, 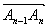 =an,则向量
=an,则向量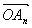 即这些向量的和,即
即这些向量的和,即
a1+a2+…+an=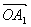 +
+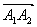 +…+
+…+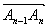 =
=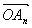 (向量加法的多边形法则)。
(向量加法的多边形法则)。
当An和O重合时(即上述折线OA1A2…An成封闭折线时),则和向量为零向量。
注意:反用以上向量的和式,即把一个向量表示为若干个向量和的形式,是解决向量问题的重要手段。
5.向量的应用
(1)向量在几何中的应用(2)向量在物理中的应用
6.主要思想与方法:
本章主要树立数形转化和结合的观点,以数代形,以形观数,用代数的运算处理几何问题,特别是处理向量的相关位置关系,正确运用共线向量和平面向量的基本定理,计算向量的模、两点的距离、向量的夹角,判断两向量是否垂直等。由于向量是一新的工具,它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查,是知识的交汇点。
-
空间向量_总结
第三章空间向量总结空间向量定义及运算直角坐标运算概念:向量模___________________________________…
-
平面向量总结
数学中,我们把这种既有大小,又有方向的量叫做向量(vector).而把那些只有大小,没有方向的量(如年龄、身高、长度、面积、体积、…
-
空间向量总结
空间向量的应用一.基本概念1.(1)用空间向量处理“平行”问题????设直线l,m的方向向量分别为a,b,平面?,?的法向量分别为…
- 平面向量计算总结
-
向量分类总结
专题四:平面向量【疑难点拨】1.与向量概念有关的问题⑴向量不同于数量,数量是只有大小的量(称标量),而向量既有大小又有方向;数量可…
-
向量总结
2.向量的概念(1)向量的基本概念①定义既有大小又有方向的量叫做向量。向量的大小也就是向量的长度,叫做向量的模。②特定大小或特定关…
-
开展“三浴”锻炼,增强幼儿体质活动的教研总结
开展“三浴”锻炼,增强幼儿体质活动教研总结依据《纲要》这一精神,我们幼儿园在20xx年x月就已经开始对幼儿进行“三浴”锻炼活动。“…
-
教研教改总结
马场中心小学20xx—20xx学年第一学期教研教改工作总结本学期我校的教研工作,以新课程实施方案为指导,遵循“科研兴教、科研兴校,…
-
20xx年九年级化学教学工作总结
本期我继续担任九年级75、76班的化学教学工作。通过一学期来的踏踏实实、认认真真的教育教学,提高了学生的学习成绩,收到了一定的教学…
-
广告业务员的月工作总结如何写
一、工作总结的结构形式及其内容年终总结(含综合性总结)或专题总结,其标题通常采用两种写法,一种是发文单位名称+时间+文种,如《铜仁…