高等数学第五章_定积分总结
第五章 定积分
创新生技102班 张梦菲
2010015066
一、 主要内容
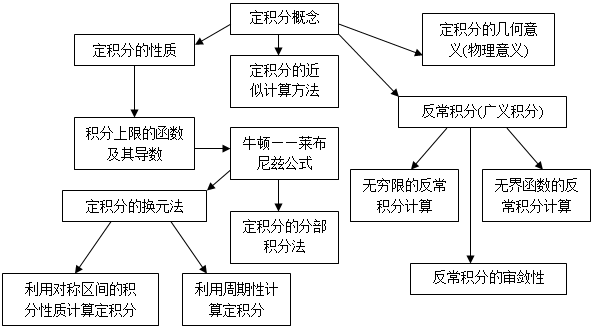
Ⅰ. 定积分概念:
- 定积分定义:设
 在区间
在区间 上有界,在
上有界,在 中任意插入若干个分点
中任意插入若干个分点
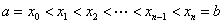 .把
.把 分成
分成 个小区间
个小区间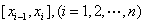 ,小区间的长度记为
,小区间的长度记为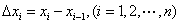 ,在
,在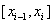 上任意取一点
上任意取一点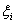 ,作
,作 ,若
,若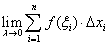
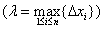 存在. 就称该极限为
存在. 就称该极限为 在
在 上的定积分.
上的定积分.
记为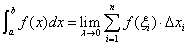
当上述极限存在时,称 在
在 上可积.
上可积.
- 若
 在
在 上连续,则
上连续,则 在
在 上可积。
上可积。 - 若
 在
在 上有界,且只有有限个间断点,则
上有界,且只有有限个间断点,则 在
在 上可积.
上可积.
Ⅱ. 定积分的几何意义
定积分 在几何上表示:由曲线
在几何上表示:由曲线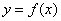 ,直线
,直线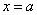 和
和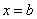 以及
以及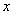 轴所围图形面积的代数和 (
轴所围图形面积的代数和 (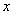 轴上方的面积取正,
轴上方的面积取正,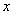 轴下方的面积取负)
轴下方的面积取负)
Ⅲ. 定积分的性质
1. 补充规定:(1)当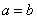 时,
时,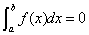
(2)当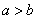 时,
时, 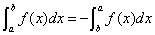
2. 性质:
(1) 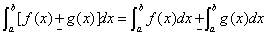
(2) 
(3) 
(4)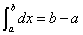
(5) 若在 上,
上,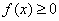 ,则
,则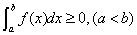
推论1:若在 上,
上,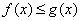 ,则
,则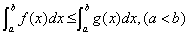 .
.
推论2: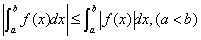 .
.
(6 ) 若在 上,
上, ,则
,则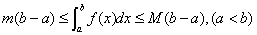
(7) (定积分中值定理):若 在
在 上连续,则在
上连续,则在 上至少存在
上至少存在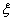 ,使
,使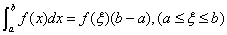 .
.
3. 连续函数 在
在 上的平均值,
上的平均值,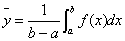
Ⅳ. 积分上限函数及其导数
1. 若对任意 ,
,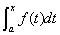 存在,则称
存在,则称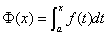 为积分上限的函数.
为积分上限的函数.
2. 若 在
在 上可积,则
上可积,则 在
在 上有界. 且积分上限函数
上有界. 且积分上限函数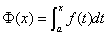 在
在 上连续.
上连续.
3. 设 在
在 上连续,则
上连续,则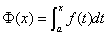 在
在 上可导,且
上可导,且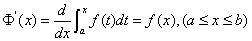 .
.
4. 设 连续,
连续, 可导,则
可导,则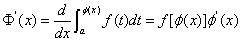 .
.
5. 设 连续,
连续, ,
,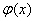 可导,则
可导,则
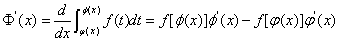 .
.
Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)
设 在
在 上连续,
上连续,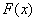 为
为 在
在 上的一个原函数,则
上的一个原函数,则
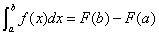 .
.
Ⅵ. 定积分的换元法
设 在
在 上连续,
上连续,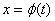 满足:
满足:
(1)  .
.
(2)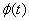 在
在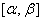 (或
(或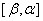 )上具有连续导数,且
)上具有连续导数,且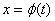 的值域不越出
的值域不越出 的范围,则有
的范围,则有 .
.
注:当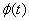 的值域
的值域 越出
越出 的范围,但满足其余条件时,只要
的范围,但满足其余条件时,只要 在
在 上连续,则换元法的结论仍然成立.
上连续,则换元法的结论仍然成立.
Ⅶ. 定积分的分部积分法
设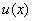 与
与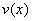 在
在 上具有连续导数,则有
上具有连续导数,则有
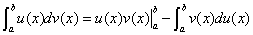
Ⅷ. 几类特殊的积分公式
1. 设 在
在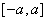 上连续,则有
上连续,则有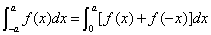 .
.

2. 设 是以
是以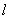 为周期的连续函数,则对任意实数
为周期的连续函数,则对任意实数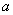 ,
,
有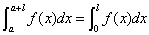 .
.
3. 设 在
在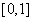 上连续,则
上连续,则
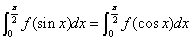

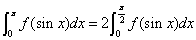
4. 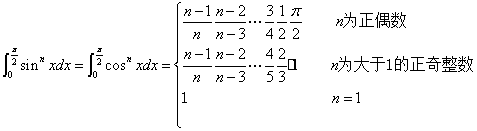
Ⅸ. 反常积分(广义积分)
1. 无穷限的反常积分
(1) 设 在
在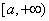 上连续,
上连续, 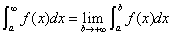
(2) 设 在
在 上连续,
上连续, 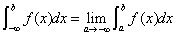
(3) 设 在
在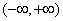 上连续,
上连续,
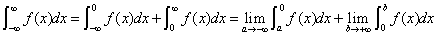
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有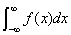 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在,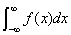 就发散.
就发散.
2. 无界函数的反常积分
(1) 设 在
在 上连续,点
上连续,点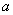 为
为 的瑕点,
的瑕点,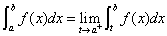
(2) 设 在
在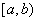 上连续,点
上连续,点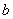 为
为 的瑕点,
的瑕点,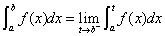
(3) 设 在
在 上除点
上除点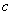
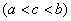 外连续,点
外连续,点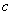 为
为 的瑕点,
的瑕点,
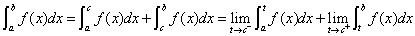
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在, 就发散.
就发散.
3. 反常积分的审敛法
(1) (比较审敛法1) 设 在
在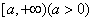 上连续,且
上连续,且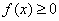 . 若存在常数
. 若存在常数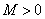 及
及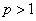 ,使得
,使得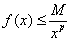
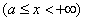 ,则反常积分
,则反常积分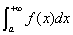 收敛;若存在常数
收敛;若存在常数 ,使得
,使得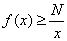
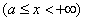 ,则反常积分
,则反常积分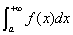 发散.
发散.
(2) (极限审敛法1) 设 在
在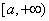 上连续,且
上连续,且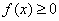 . 若存在常数
. 若存在常数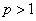 ,使得
,使得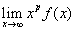 存在,则反常积分
存在,则反常积分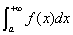 收敛;若
收敛;若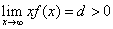 ,
,
(或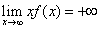 )则反常积分
)则反常积分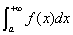 发散.
发散.
(3) (比较审敛法2)设 在
在 上连续,且
上连续,且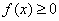 .
. 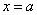 为
为 的瑕点.若存在常数
的瑕点.若存在常数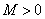 及
及 ,使得
,使得 ,则反常积分
,则反常积分 收敛;若存在常数
收敛;若存在常数 ,使得
,使得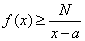
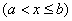 ,则反常积分
,则反常积分 发散.
发散.
(4) (极限审敛法2) 设 在
在 上连续,且
上连续,且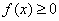 .
. 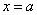 为
为 的瑕点. 若存在常数
的瑕点. 若存在常数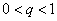 ,使得
,使得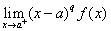 存在,则反常积分
存在,则反常积分 收敛;若
收敛;若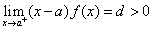 ,(或
,(或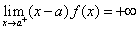 )则反常积分
)则反常积分 发散.
发散.
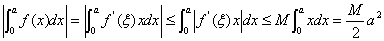 .
.
第二篇:高等数学第二章导数知识总结
高等数学第二章知识总结
在这一章里需要掌握的是求一阶导数的多种方法和求高阶导数的计算公式。微分和导数的关系
求导数与求微分方法相同,只不过在求微分时要在后面加上dx.
函数在某点处的导数就是函数在该点处的变化率. 导数有很多种表现形式.
一.
(1) 单侧导数 即左 右导数.
函数可导的充要条件是:左右导数存在且相等.
(2) 可导与连续的关系:可导必然连续,连续不一定可导.
注:函数的导数就是函数在某点处因变量与自变量比值的极限.
◆求导数的方法有:
(1) 利用导数的定义.(简单一点就是△y/△x的极
限)
(2) 利用导数的几何意义解决几何及物理,化学的
实际问题.
(3) 利用初等函数的求导公式.(在书P59)
(4) 利用反函数求导法.(反函数的导数就是原函数
导数的倒数.)
(5) 利用复合函数求导法.(由外到内,逐层求导)
(6) 利用隐函数求导法
(7) 利用参数方程确定函数的求导法.
(8) 利用分段函数求导法.
(9) 利用函数连续,可导的定义,研究讨论函数的连
续性与可导性.
二.高阶导数
高阶导数可细分为:一阶导数,二阶导数,三阶导数……N阶导数等等.(一阶导数的导数是二阶导数) 应该掌握的是高阶导数的运算.
方法有两种:(1)直接法.(2)间接法.
间接法适用于阶数较高的运算.其规律性较强. 常用的高阶导数公式在书P63上.注意查看.
■计算uv相乘形式的高阶导数时,首先要判断u,v从一阶到n阶的结果,再运用莱布尼兹公式求出结果。
三.隐函数和由参数方程确定的函数的导数 什么是隐函数?
如果变量x,y的函数关系可以用一个二元方程表示,且对在给定范围内的每一个x,通过方程有确定的y与之对应,即Y是X的函数,这种函数就叫做隐函数
F(x,y)=0
从二元方程中解出y的值,就是隐函数的显化. 有些隐函数不易显化,甚至不能显化.
隐函数的求导方法:(例题在书P66 例40,41)
(1) 把y看做是复合函数的中间变量,把y看作y(x)
即可。再在方程两边分别对X求导.
(2) 从求导后的方程中求出y’.
(3) 在隐函数的求导结果中允许含有y,但是求某一
以知点的导数时不仅要代X的值,还要代Y的值. 对数求导法:先两边取对数,再关于X求导.例题在书P68,例44(遇到指数形式的函数时就采用此类方法)
对参数方程确定的函数求导方法很简单,就是用y’/x’.
四.函数的微分.
可微就可导,可导就可微.
求函数的微分就是对函数求导,主要就是在所求结果后面加上dx.
微分的几何意义是某点处的切线纵坐标的增量.
常用的微分公式在书P76.
五.微分的应用.
1.微分在近似计算,误差估计中的应用.在书P80 P81.
-
考研.数学 高等数学总结1
中值定理及应用一、基本概念定理1、极值点与极值—设连续y?f(x)(x?D),其中x0?D。若存在??0,当0?|x?x0|??时…
-
高数上册知识点总结
高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(y?ax),三…
-
同济六版上册高数总结(一些重要公式及知识点)
同济六版上册高数总结微分公式与积分公式(tgx)??secx(ctgx)???csc2x(secx)??secx?tgx(cscx…
-
高数总结和考试重点罗列
总结高分经验我认为有以下几点要引起注意一一定要夯实基础不放过书上的每一道题书中例题自己要先试着做一下然后再看答案每一章看完之后再翻…
-
高数总结
高等数学B期末课程总结班级11网工2班系别计算机科学与技术高数知识点总结高数的学习又到了尾声也是时候总结本学期学了哪些知识点既是对…
-
高数积分总结
第四章一元函数的积分及其应用第一节不定积分一、原函数与不定积分的概念定义1.设f(x)是定义在某区间的已知函数,若存在函数F(x)…
-
不定积分解法总结
不定积分解题方法总结不定积分看似形式多样,变幻莫测,但并不是毫无解题规律可言。本文所总结的是一般规律,并非所有相似题型都适用,具体…
-
不定积分基础总结
不定积分不定积分中需了解的知识点1、原函数、原函数存在定理、定义原函数(定义):设函数?x?在某区间I上有效,如果存在函数F?x?…
-
定积分知识点总结
定积分基础知识点与方法总结1.知识网络2.方法总结(1)定积分的定义:分割—近似代替—求和—取极限(2)定积分几何意义:①?f(x…
-
不定积分方法总结 2
不定积分方法总结一.一个重要思想拆分:用各种变换将一个合式分解成多个分式,这些分式的积分往往是好求的,再对每个分式进行积分,从而达…
-
高等数学积分总结
?问题引例:曲边梯形的面积、变速直线运动的路程?n?积分定义:bf?x?dx?lim?f????xii?a??0?i?1?b?计算…