高考复数知识点精华总结
复 数
1.复数的概念:
(1)虚数单位i;
(2)复数的代数形式z=a+bi,(a, b∈R);
(3)复数的实部、虚部、虚数与纯虚数。
2.复数集
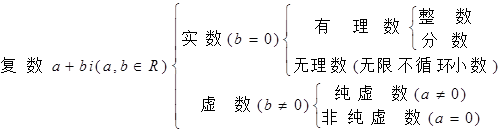
3.复数a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位,当b=0时,a+bi就是实数,当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。
应特别注意,a=0仅是复数a+bi为纯虚数的必要条件,若a=b=0,则a+bi=0是实数。
4.复数的四则运算
若两个复数z1=a1+b1i,z2=a2+b2i,
(1)加法:z1+z2=(a1+a2)+(b1+b2)i;
(2)减法:z1-z2=(a1-a2)+(b1-b2)i;
(3)乘法:z1·z2=(a1a2-b1b2)+(a1b2+a2b1)i;
(4)除法: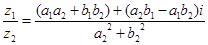 ;
;
(5)四则运算的交换率、结合率;分配率都适合于复数的情况。
(6)特殊复数的运算:
①  (n为整数)的周期性运算; ②(1±i)2 =±2i;
(n为整数)的周期性运算; ②(1±i)2 =±2i;
③ 若ω=- +
+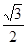 i,则ω3=1,1+ω+ω2=0.
i,则ω3=1,1+ω+ω2=0.
5.共轭复数与复数的模
(1)若z=a+bi,则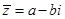 ,
,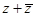 为实数,
为实数,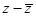 为纯虚数(b≠0).
为纯虚数(b≠0).
(2)复数z=a+bi的模|Z|=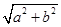 , 且
, 且 =a2+b2.
=a2+b2.
6.根据两个复数相等的定义,设a, b, c, d∈R,两个复数a+bi和c+di相等规定为a+bi=c+di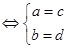 . 由这个定义得到a+bi=0
. 由这个定义得到a+bi=0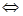
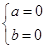 .
.
两个复数不能比较大小,只能由定义判断它们相等或不相等。
4.复数a+bi的共轭复数是a-bi,若两复数是共轭复数,则它们所表示的点关于实轴对称。若b=0,则实数a与实数a共轭,表示点落在实轴上。
5.复数的加法、减法、乘法运算与实数的运算基本上没有区别,最主要的是在运算中将i2=-1结合到实际运算过程中去。
如(a+bi)(a-bi)= a2+b2
6.复数的除法是复数乘法的逆运算将满足(c+di)(x+yi)=a+bi (c+bi≠0)的复数x+yi叫做复数a+bi除以复数c+di的商。
由于两个共轭复数的积是实数,因此复数的除法可以通过将分母实化得到,即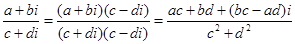 .
.
7.复数a+bi的模的几何意义是指表示复数a+bi的点到原点的距离。
(二)典型例题讲解
1.复数的概念
例1.实数m取什么数值时,复数z=m+1+(m-1)i是(1)实数?(2)虚数?(3)纯虚数?(4)对应的点Z在第三象限?
解:复数z=m+1+(m-1)i中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,
∴ (1)m=1时,z是实数; (2)m≠1时,z是虚数;
(3)当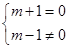 时,即m=-1时,z是纯虚数;
时,即m=-1时,z是纯虚数;
(4)当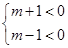 时,即m<-1时,z对应的点Z在第三象限。
时,即m<-1时,z对应的点Z在第三象限。
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y.
解:根据复数相等的意义,得方程组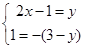 ,得x=
,得x= , y=4.
, y=4.
例4.当m为何实数时,复数z=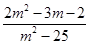 +(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
+(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
解:此题主要考查复数的有关概念及方程(组)的解法.
(1)z为实数,则虚部m2+3m-10=0,即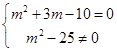 ,
,
解得m=2,∴ m=2时,z为实数。
(2)z为虚数,则虚部m2+3m-10≠0,即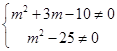 ,
,
解得m≠2且m≠±5. 当m≠2且m≠±5时,z为虚数.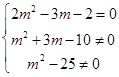 ,
,
解得m=- , ∴当m=-
, ∴当m=- 时,z为纯虚数.
时,z为纯虚数.
诠释:本题应抓住复数分别为实数、虚数、纯虚数时相应必须具备的条件,还应特别注意分母不为零这一要求.
例5.计算:i+i2+i3+……+i2005.
解:此题主要考查in的周期性.
i+i2+i3+……+i2005=(i+i2+i3+i4)+……+(i2001+i2002+ i2003+i2004)+i2005
=(i-1-i+1)+ (i-1-i+1)+……+(i-1-i+1)+i
=0+0+……+0+i=i.
或者可利用等比数列的求和公式来求解(略) 诠释:本题应抓住in的周期及合理分组.
例8.使不等式m2-(m2-3m)i<(m2-4m+3)i+10成立的实数m= .
解:此题主要考查复数能比较大小的条件及方程组和不等式的解法.
∵ m2-(m2-3m)i<(m2-4m+3)i+10, 且虚数不能比较大小,
∴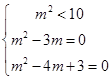 ,解得
,解得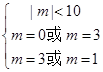 ,∴ m=3.
,∴ m=3.
当m=3时,原不等式成立.
诠释:本题应抓住复数能比较大小时必须都为实数这一条件。
例9.已知z=x+yi(x,y∈R),且 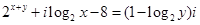 ,求z.
,求z.
解:本题主要考查复数相等的充要条件及指数方程,对数方程的解法.
∵ 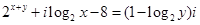 ,∴
,∴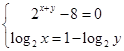 ,∴
,∴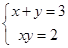 ,
,
解得 或
或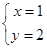 , ∴ z=2+i或z=1+2i.
, ∴ z=2+i或z=1+2i.
诠释:本题应抓住复数相等的充要条件这一关键,正确、熟练地解方程(指数,对数方程)
例10.已知x为纯虚数,y是实数,且2x-1+i=y-(3-y)i,求x、y的值.
解:本题主要考查复数的有关概念,实数与i的运算,复数相等的充要条件,方程组的解法.
设x=ti (t∈R,且t≠0),则2x-1+i=y-(3-y)i可化为
2ti-1+i=y-(3-y)i,即(2t+1)i-1=y-(3-y)i,
∴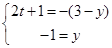 , ∴y=-1, t=-
, ∴y=-1, t=- , ∴ x=-
, ∴ x=- i.
i.
2.复数的四则运算
例1.计算:
(1)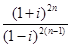 ,n∈N+;
,n∈N+;
(2)若ω=- +
+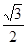 i,ω3=1,计算
i,ω3=1,计算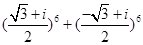 ;
;
(3)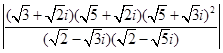 ;
;
(4)S=1+2i+3i2+4i3+……+100i99.
解:(1)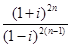 =
=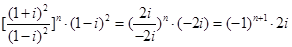
=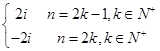 .
.
(2)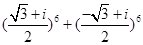 =
=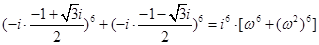
=-2.
(3)由于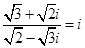 ,
, 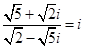 ,
,
∴ 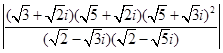 =
=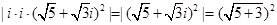
=8.
(4)S=1+2i+3i2+4i3+……+100i99
=(1+2i+3i2+4i3)+(5i4+6i5+7i6+8i7)+……+(97i96+98i97+99i98+100i99)
=(1+2i-3-4i)+(5+6i-7-8i)+……+(97+98i-99-100i)
=25(-2-2i)=-50-50i.
例2.已知复数z满足|z-2|=2,z+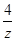 ∈R,求z.
∈R,求z.
解:设z=x+yi, x, y∈R,则
z+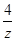 =z+
=z+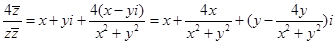 ,
,
∵ z+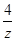 ∈R,∴
∈R,∴ 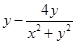 =0, 又|z-2|=2, ∴ (x-2)2+y2=4,
=0, 又|z-2|=2, ∴ (x-2)2+y2=4,
联立解得,当y=0时, x=4或x=0 (舍去x=0, 因此时z=0),
当y≠0时, 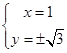 , z=1±
, z=1±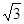 ,
,
∴ 综上所得 z1=4,z2=1+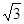 i,z3=1-
i,z3=1-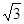 i.
i.
例3.设z为虚数,求证:z+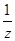 为实数的充要条件是|z|=1.
为实数的充要条件是|z|=1.
证明:设z=a+bi (a, b∈R,b≠0),于是
z+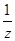 =(a+bi)+
=(a+bi)+ ,
,
所以b≠0, (z+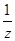 )∈R
)∈R b-
b- =0
=0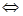 a2+b2=1
a2+b2=1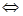 |z|=1.
|z|=1.
例4.复数z满足(z+1)( +1)=|
+1)=| |2,且
|2,且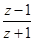 为纯虚数,求z.
为纯虚数,求z.
解:设z=x+yi (x, y∈R),则
(z+1)( +1)=|
+1)=| |2+z+
|2+z+ +1=|
+1=| |2,∴ z+
|2,∴ z+ +1=0,z+
+1=0,z+ =-1,x=-
=-1,x=- .
.
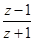 =
=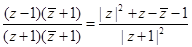 =
= 为纯虚数,
为纯虚数,
∴ x2+y2-1=0, y=±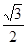 , ∴ z=-
, ∴ z=- +
+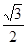 i或z=-
i或z=- -
-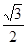 i.
i.
例5.复数z满足(1+2i)z+(3-10i) =4-34i,求z.
=4-34i,求z.
解:设z=x+yi (x, y∈R),则(1+2i)(x+yi)+(3-10i)(x-yi) =4-34i,
整理得(4x-12y)-(8x+2y)i=4-34i.
∴ 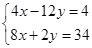 , 解得
, 解得 , ∴ z=4+i.
, ∴ z=4+i.
例6.设z是虚数,ω=z+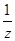 是实数,且-1<ω<2,
是实数,且-1<ω<2,
(1)求|z|的值及z的实部的取值范围;(2)设u=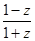 ,求证u为 纯虚数;
,求证u为 纯虚数;
(3)求ω-u2的最小值。
解:(1)设z=a+bi (a, b∈R, b≠0),则
ω=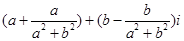 ,由于ω是实数且b≠0,∴ a2+b2=1,
,由于ω是实数且b≠0,∴ a2+b2=1,
即|z|=1,由ω=2a, -1<ω<2, ∴ z的实部a的的取值范围是(- , 1).
, 1).
(2)u=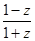 =
=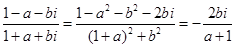 ,由于a∈(-
,由于a∈(- , 1), b≠0,
, 1), b≠0,
∴ u是纯虚数。
(3)ω-u2=2a+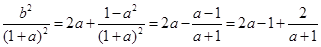
=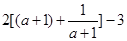 ,
,
由于a∈(- , 1),∴ a+1>0,则ω-u2≥2×2-3=1,
, 1),∴ a+1>0,则ω-u2≥2×2-3=1,
当a+1= , 即a=0时,上式取等号,所以ω-u2的最小值为1.
, 即a=0时,上式取等号,所以ω-u2的最小值为1.
例7.证明: =1.
=1.
解:此题考查复数的运算、模的定义,共轭复数的性质等.
设z=a+bi,(a, b∈R),则
 =
=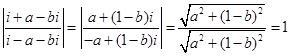 .
.
解2:∵  ,∴
,∴  =
=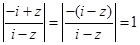 .
.
第二篇:高考复数知识点精华总结
复 数
1.复数的概念:
(1)虚数单位i;
(2)复数的代数形式z=a+bi,(a, b∈R);
(3)复数的实部、虚部、虚数与纯虚数。
2.复数集
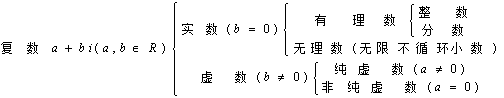
3.复数a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位,当b=0时,a+bi就是实数,当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。
应特别注意,a=0仅是复数a+bi为纯虚数的必要条件,若a=b=0,则a+bi=0是实数。
4.复数的四则运算
若两个复数z1=a1+b1i,z2=a2+b2i,
(1)加法:z1+z2=(a1+a2)+(b1+b2)i;
(2)减法:z1-z2=(a1-a2)+(b1-b2)i;
(3)乘法:z1·z2=(a1a2-b1b2)+(a1b2+a2b1)i;
(4)除法: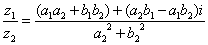 ;
;
(5)四则运算的交换率、结合率;分配率都适合于复数的情况。
(6)特殊复数的运算:
①  (n为整数)的周期性运算; ②(1±i)2 =±2i;
(n为整数)的周期性运算; ②(1±i)2 =±2i;
③ 若ω=-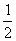 +
+ i,则ω3=1,1+ω+ω2=0.
i,则ω3=1,1+ω+ω2=0.
5.共轭复数与复数的模
(1)若z=a+bi,则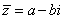 ,
,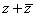 为实数,
为实数, 为纯虚数(b≠0).
为纯虚数(b≠0).
(2)复数z=a+bi的模|Z|=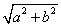 , 且
, 且 =a2+b2.
=a2+b2.
6.根据两个复数相等的定义,设a, b, c, d∈R,两个复数a+bi和c+di相等规定为a+bi=c+di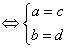 . 由这个定义得到a+bi=0
. 由这个定义得到a+bi=0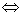
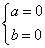 .
.
两个复数不能比较大小,只能由定义判断它们相等或不相等。
4.复数a+bi的共轭复数是a-bi,若两复数是共轭复数,则它们所表示的点关于实轴对称。若b=0,则实数a与实数a共轭,表示点落在实轴上。
6.复数的除法是复数乘法的逆运算将满足(c+di)(x+yi)=a+bi (c+bi≠0)的复数x+yi叫做复数a+bi除以复数c+di的商。
由于两个共轭复数的积是实数,因此复数的除法可以通过将分母实化得到,即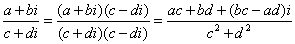 .
.
7.复数a+bi的模的几何意义是指表示复数a+bi的点到原点的距离。
(二)典型例题讲解
1.复数的概念
例1.实数m取什么数值时,复数z=m+1+(m-1)i是(1)实数?(2)虚数?(3)纯虚数?(4)对应的点Z在第三象限?
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y.
例4.当m为何实数时,复数z= +(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
+(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
例5.计算:i+i2+i3+……+i2005.
例8.使不等式m2-(m2-3m)i<(m2-4m+3)i+10成立的实数m= .
例9.已知z=x+yi(x,y∈R),且 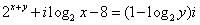 ,求z.
,求z.
例10.已知x为纯虚数,y是实数,且2x-1+i=y-(3-y)i,求x、y的值.
2.复数的四则运算
例1.计算:
(1)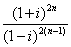 ,n∈N+;
,n∈N+;
(2)若ω=-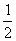 +
+ i,ω3=1,计算
i,ω3=1,计算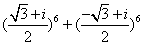 ;
;
(3)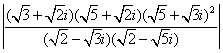 ;
;
(4)S=1+2i+3i2+4i3+……+100i99.
例2.已知复数z满足|z-2|=2,z+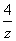 ∈R,求z.
∈R,求z.
例4.复数z满足(z+1)(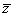 +1)=|
+1)=|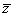 |2,且
|2,且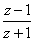 为纯虚数,求z.
为纯虚数,求z.
例5.复数z满足(1+2i)z+(3-10i)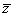 =4-34i,求z.
=4-34i,求z.
例6.设z是虚数,ω=z+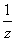 是实数,且-1<ω<2,
是实数,且-1<ω<2,
(1)求|z|的值及z的实部的取值范围;(2)设u=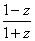 ,求证u为 纯虚数;
,求证u为 纯虚数;
(3)求ω-u2的最小值。
7.已知关于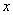 的方程
的方程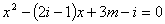 有实根,求实数
有实根,求实数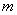 的取值。
的取值。
1..若复数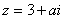 满足条件
满足条件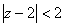 ,则实数
,则实数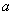 的取值范围是( )
的取值范围是( )
A.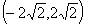 B.
B.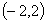 C.
C.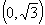 D.
D.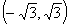
3.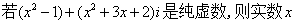 的值为 ( )
的值为 ( )
 .
.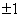
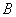 .1
.1 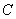 .
.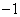
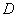 .
. 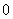
8.如果复数z=(a2-3a+2)+(a-1)i为纯虚数,则实数a的值 ( ).
A.等于1或2 B.等于1 C.等于2 D.不存在
13.已知 ,其中
,其中 ,则
,则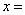 ,
,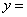 .
.
14.复数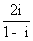 在复平面内所对应的点的坐标为 .
在复平面内所对应的点的坐标为 .
15.设复数z满足i(z+1)=-3+2i(i为虚数单位),则z等于___ _____.
16.若复数z满足z=i(2-z)(i是虚数单位),则z=________.
17.(本题满分12分)已知 ,复数
,复数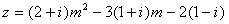 ,
,
(1)写出复数z的代数形式;
(2)当m为何值时,z=0?当m为何值时,z是纯虚数?
-
考研高数知识点总结 第一单元 函数
第一单元函数1.1函数函数是变量与变量的一种对应关系。本书变量均取值于实数。1.1.1实数实数:有理数(分数)和无理数(无限不循环…
-
高等数学知识点总结
高等数学知识点总结导数公式2tanxsecxctanxcscxsecxsecxtanxcscxcscxcotxaalnalogax…
-
高数上册知识点总结
高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(y?ax),三…
-
高数知识点总结(1)
北雁高数知识点总结QQ7607220xxEmailheblyd163com专接本高数知识点总结上册北雁友情提供函数极限与连续性数列…
-
考研高数精华知识点总结:两个重要极限
凯程考研历史悠久专注考研科学应试严格管理成就学员考研高数精华知识点总结两个重要极限高等数学是考研数学考试中内容最多的一部分分值所占…
-
复数知识点精心总结
复数知识点考试内容:复数的概念.复数的加法和减法.复数的乘法和除法.数系的扩充.考试要求:(1)了解复数的有关概念及复数的代数表示…
-
复数知识点总结
复数一、复数的概念1.虚数单位i(1)它的平方等于?1,即i??1;(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘法…
-
高中数学复数专题知识点整理和总结人教版
【1】复数的基本概念(1)形如a+bi的数叫做复数(其中a,b?R);复数的单位为i,它的平方等于-1,即i2??1.其中a叫做复…
-
高中数学第十五章知识点总结(精华版) 复数
高中数学第十五章复数考试内容:复数的概念.复数的加法和减法.复数的乘法和除法.数系的扩充.考试要求:(1)了解复数的有关概念及复数…
-
高中数学复数专题知识点整理和总结人教版
专题二复数一.基本知识【1】复数的基本概念(1)形如a+bi的数叫做复数(其中a,b?R);复数的单位为i,它的平方等于-1,即i…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…