概率论知识点总结
概率论知识点总结
第一章 随机事件及其概率
第一节 基本概念
随机实验:将一切具有下面三个特点:(1)可重复性(2)多结果性(3)不确定性的试验或观察称为随机试验,简称为试验,常用 E 表示。
随机事件:在一次试验中,可能出现也可能不出现的事情(结果)称为随机事件,简称为事件。
不可能事件:在试验中不可能出现的事情,记为Ф。
必然事件:在试验中必然出现的事情,记为Ω。
样本点:随机试验的每个基本结果称为样本点,记作ω.
样本空间:所有样本点组成的集合称为样本空间. 样本空间用Ω表示.
一个随机事件就是样本空间的一个子集。基本事件—单点集,复合事件—多点集
一个随机事件发生,当且仅当该事件所包含的一个样本点出现。
事件的关系与运算(就是集合的关系和运算)
包含关系:若事件 A 发生必然导致事件B发生,则称B包含A,记为 或
或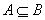 。
。
相等关系:若 且
且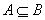 ,则称事件A与事件B相等,记为A=B。
,则称事件A与事件B相等,记为A=B。
事件的和:“事件A与事件B至少有一个发生”是一事件,称此事件为事件A与事件B的和事件。记为 A∪B。
事件的积:称事件“事件A与事件B都发生”为A与B的积事件,记为A∩ B或AB。
事件的差:称事件“事件A发生而事件B不发生”为事件A与事件B的差事件,记为 A-B。
用交并补可以表示为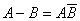 。
。
互斥事件:如果A,B两事件不能同时发生,即AB=Φ,则称事件A与事件B是互不相容事件或互斥事件。互斥时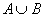 可记为A+B。
可记为A+B。
对立事件:称事件“A不发生”为事件A的对立事件(逆事件),记为 。对立事件的性质:
。对立事件的性质: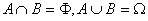 。
。
事件运算律:设A,B,C为事件,则有
(1)交换律:A∪B=B∪A,AB=BA
(2)结合律:A∪(B∪C)=(A∪B)∪C=A∪B∪C A(BC)=(AB)C=ABC
(3)分配律:A∪(B∩C)=(A∪B)∩(A∪C) A(B∪C)=(A∩B)∪(A∩C)= AB∪AC
(4)对偶律(摩根律):

第二节 事件的概率
概率的公理化体系:
(1)非负性:P(A)≥0;
(2)规范性:P(Ω)=1
(3)可数可加性: 两两不相容时
两两不相容时

概率的性质:
(1)P(Φ)=0
(2)有限可加性: 两两不相容时
两两不相容时

当AB=Φ时P(A∪B)=P(A)+P(B)
(3)
(4)P(A-B)=P(A)-P(AB)
(5)P(A∪B)=P(A)+P(B)-P(AB)
第三节 古典概率模型
1、设试验E是古典概型, 其样本空间Ω由n个样本点组成,事件A由k个样本点组成.则定义事件A的概率为
2、几何概率:设事件A是Ω的某个区域,它的面积为 μ(A),则向区域Ω上随机投掷一点,该点落在区域 A 的概率为
假如样本空间Ω可用一线段,或空间中某个区域表示,则事件A的概率仍可用上式确定,只不过把μ理解为长度或体积即可.
第四节 条件概率
条件概率:在事件B发生的条件下,事件A发生的概率称为条件概率,记作 P(A|B).

乘法公式:P(AB)=P(B)P(A|B)=P(A)P(B|A)
全概率公式:设 是一个完备事件组,则P(B)=∑P(
是一个完备事件组,则P(B)=∑P( )P(B|
)P(B| )
)
贝叶斯公式:设 是一个完备事件组,则
是一个完备事件组,则

第五节 事件的独立性
两个事件的相互独立:若两事件A、B满足P(AB)= P(A) P(B),则称A、B独立,或称A、B相互独立.
三个事件的相互独立:对于三个事件A、B、C,若P(AB)= P(A) P(B),P(AC)= P(A)P(C),P(BC)= P(B) P(C),P(ABC)= P(A) P(B)P(C),则称A、B、C相互独立
三个事件的两两独立:对于三个事件A、B、C,若P(AB)= P(A) P(B),P(AC)= P(A)P(C),P(BC)= P(B) P(C),则称A、B、C两两独立
独立的性质:若A与B相互独立,则 与B,A与
与B,A与 ,
, 与
与 均相互独立
均相互独立
总结:1.条件概率是概率论中的重要概念,其与独立性有密切的关系,在不具有独立性的场合,它将扮演主要的角色。2.乘法公式、全概公式、贝叶斯公式在概率论的计算中经常使用, 应牢固掌握。3.独立性是概率论中的最重要概念之一,应正确理解并应用于概率的计算。
第二章 一维随机变量及其分布
第二节 分布函数
分布函数:设X是一个随机变量,x为一个任意实数,称函数 为X的分布函数。如果将X看作数轴上随机点的坐标,那么分布函数 F(x)的值就表示X落在区间
为X的分布函数。如果将X看作数轴上随机点的坐标,那么分布函数 F(x)的值就表示X落在区间  内的概率
内的概率
分布函数的性质:(1)单调不减;(2)右连续;(3)
第三节 离散型随机变量
离散型随机变量的分布律:设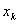 (k=1,2, …)是离散型随机变量X所取的一切可能值,称
(k=1,2, …)是离散型随机变量X所取的一切可能值,称  为离散型随机变量X的分布律,也称概率分布.
为离散型随机变量X的分布律,也称概率分布.
当离散性随机变量取值有限且概率的规律不明显时,常用表格形式表示分布律。
分布律的性质:(1) ;(2)
;(2)
离散型随机变量的概率计算:
(1)已知随机变量X的分布律,求X的分布函数;

(2)已知随机变量X的分布律, 求任意随机事件的概率;
(3)已知随机变量X的分布函数,求X的分布律

三种常用离散型随机变量的分布:
1.(0-1)分布:参数为p的分布律为
2.二项分布:参数为n,p的分布律为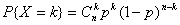 ,
, 。例如n重独立重复实验中,事件A发生的概率为p,记X为这n次实验中事件A发生的次数,则X~B(n,p)
。例如n重独立重复实验中,事件A发生的概率为p,记X为这n次实验中事件A发生的次数,则X~B(n,p)
3.泊松分布:参数为λ的分布率为 ,
, 。例如记X为某段事件内电话交换机接到的呼叫次数,则X~P(λ)
。例如记X为某段事件内电话交换机接到的呼叫次数,则X~P(λ)
第四节 连续型随机变量
连续型随机变量概率密度f(x)的性质
(1)f(x)≥0
(2) ,
,
(3)
(4)
连续型随机变量的概率计算:
(1)已知随机变量X的密度函数,求X的分布函数;
(2)已知随机变量X的分布函数,求X的密度函数;
(3)已知随机变量X的密度函数, 求随机事件的概率;
(4)已知随机变量X的分布函数,求随机事件的概率;
三种重要的连续型分布:
1.均匀分布:密度函数 ,记为 X~U[a,b].
,记为 X~U[a,b].
2. 指数分布:密度函数 ,记为X~E(λ)
,记为X~E(λ)
3. 正态分布:密度函数 ,记为
,记为
N(0,1)称为标准正态分布.标准正态分布的重要性在于,任何一个一般的正态分布都可以通过线性变换转化为标准正态分布,然后再计算概率.

第五节 随机变量函数的分布
离散型:在分布律的表格中直接求出;
连续型:寻找分布函数间的关系,再求导得到密度函数间的关系;注意分段函数情况可能需要讨论,得到的结果也可能是分段函数。

第三章 多维随机变量及其分布
第一节 二维随机变量的联合分布函数
联合分布函数 ,表示随机点落在以(x ,y)为顶点的左下无穷矩形区域内的概率。
,表示随机点落在以(x ,y)为顶点的左下无穷矩形区域内的概率。
联合分布函数的性质:
(1)分别关于x和y单调不减;
(2)分别关于x和y右连续;
(3)F (-∞ , y ) = 0,F ( x ,-∞ ) =0,F(-∞,-∞) = 0
F ( +∞ ,+∞ ) = 1
第二节 二维离散型随机变量
联合分布律:
联合分布律的性质: ;
;
第三节 二维连续性随机变量
联合密度:
联合密度的性质: ;
; ;
;
第四节 边缘分布
二维离散型随机变量的边缘分布律:在表格边缘,对应概率相加求出;
二维连续性随机变量的边缘密度:先求出边缘分布函数,在求导求出边缘密度
第六节 随机变量的独立性
独立性判断:
(1)若 取值互不影响,可认为相互独立;
取值互不影响,可认为相互独立;
(2)根据独立性定义判断
离散型可用
连续型可用
独立性的应用:(1)判断独立性;(2)已知独立性,由边缘分布确定联合分布
第四章 随机变量的数字特征
离散型随机变量数学期望的计算 ,
,
连续型随机变量数学期望的计算 ,
,
方差的计算: ,
,
数学期望的性质
(1)E (C ) = C
(2)E (CX ) = CE (X )
(3)E (X + Y ) = E (X ) + E (Y )
(4)当 X ,Y 独立时,E (X Y ) = E (X )E (Y )
方差的性质
(1)D (C) = 0
(2)D (CX ) =  D(X)
D(X)
(3)若 X ,Y 相互独立,则D ( X ± Y ) = D ( X ) + D (Y )
常见分布的数学期望和方差
两点分布,二项分布,泊松分布,均匀分布,正态分布,指数分布
第二篇:概率论知识点总结
概率论与数理统计期末知识点小结
第一章 概率论的基本概念
1. 随机试验
确定性现象:在自然界中一定发生的现象称为确定性现象。
随机现象: 在个别实验中呈现不确定性,在大量实验中呈现统计规律性,这种现象称
为随机现象。
随机试验:为了研究随机现象的统计规律而做的的实验就是随机试验。
随机试验的特点:1)可以在相同条件下重复进行;
2)每次试验的可能结果不止一个,并且能事先明确试验的所有可能
结果;
3)进行一次试验之前不能确定哪一个结果会先出现;
2. 样本空间、随机事件
样本空间:我们将随机试验E的所有可能结果组成的集合称为E的样本空间,记为S。 样本点:构成样本空间的元素,即E中的每个结果,称为样本点。
事件之间的基本关系:包含、相等、和事件(并)、积事件(交)、差事件(A-B:包含A
不包含B)、互斥事件(交集是空集,并集不一定是全集)、对立
事件(交集是空集,并集是全集,称为对立事件)。
事件之间的运算律:交换律、结合律、分配率、摩根定理(通过韦恩图理解这些定理)
3. 频率与概率
频数:事件A发生的次数
频率:频数/总数
概率:当重复试验的次数n逐渐增大,频率值就会趋于某一稳定值,这个值就是概率。 概率的特点:1)非负性。2)规范性。3)可列可加性。
概率性质:1)P(空集)=0,2)有限可加性,3)加法公式:P(A+B)=P(A)+P(B)
-P(AB)
4. 古典概型
学会利用排列组合的知识求解一些简单问题的概率(彩票问题,超几何分布,分配问题,
插空问题,捆绑问题等等)
5. 条件概率
定义:A事件发生条件下B发生的概率P(B|A)=P(AB)/P(A)
乘法公式:P(AB)=P(B|A)P(A)
全概率公式与贝叶斯公式
6. 独立性检验
设 A、B是两事件,如果满足等式
P(AB)=P(A)P(B)
则称事件A、B相互独立,简称A、B独立。
第二章.随机变量及其分布
1. 随机变量
定义:设随机试验的样本空间为S={e}. X=X(e)是定义在样本空间S上的单值函数,称
X=X(e)为随机变量。
2. 离散型随机变量及其分布律
三大离散型随机变量的分布
1)(0——1)分布。E(X)=p, D(X )=p(1-p)
2)伯努利试验、二项分布 E(X)=np, D(X)=np(1-p)
3) 泊松分布 P(X=k)= (?^k)e^(- ?)/k! (k=0,1,2,……)
E(X)=?,D(X)= ?
注意:当二项分布中n 很大时,可以近似看成泊松分布,即np= ?
3. 随机变量的分布函数
定义:设X是一个随机变量,x是任意的实数,函数
F(x)=P(X≤x),x属于R 称为X的分布函数
分布函数的性质:
1) F(x)是一个不减函数
2) 0≤F(x)≤1
离散型随机变量的分布函数的求法(由分布律求解分布函数)
连续性随机变量的分布函数的求法(由分布函数的图像求解分布函数,由概率密度求
解分布函数)
4. 连续性随机变量及其概率密度
连续性随机变量的分布函数等于其概率密度函数在负无穷到x的变上限广义积分 相反密度函数等与对应区间上分布函数的导数
密度函数的性质:1)f(x)≥0
2) 密度函数在负无穷到正无穷上的广义积分等于1
三大连续性随机变量的分布: 1)均与分布 E(X)=(a+b)/2 D (X)=[(b-a)^2]/12
2)指数分布 E(X)=θ D(X)=θ^2
3)正态分布一般式(标准正态分布)
5. 随机变量的函数的分布
1)已知随机变量X的 分布函数求解Y=g(X)的分布函数
2)已知随机变量X的 密度函数求解Y=g(X)的密度函数
第三章 多维随机变量及其分布(主要讨论二维随机变量的分布)
1.二维随机变量
定义 设(X,Y)是二维随机变量,对于任意实数x, y,二元函数
F(x, Y)=P[(X≤x)交(Y≤y)] 称为二维随机变量(X,Y)的分布函数或称为随机变量联合分布函数
离散型随机变量的分布函数和密度函数
连续型随机变量的分布函数和密度函数
重点掌握利用二重积分求解分布函数的方法
2.边缘分布
离散型随机变量的边缘概率
连续型随机变量的边缘概率密度
3.相互独立的随机变量
如果X,Y相互独立,那么X,Y的联合概率密度等于各自边缘的乘积
5. 两个随机变量的分布函数的分布
关键掌握利用卷积公式求解Z=X+Y的概率密度
第四章.随机变量的数字特征
1.数学期望
离散型随机变量和连续型随机变量数学期望的求法
六大分布的数学期望
2.方差
连续性随机变量的方差
D(X)=E(X^2)-[E (X )]^2
方差的基本性质:
1) 设C是常数,则D(C)=0
2) 设X随机变量,C是常数,则有
D(CX)=C^2D(X)
3) 设X,Y是两个随机变量,则有
D(X+Y)=D(X)+D(Y)+2E{(X-E(X))(Y-E(Y))} 特别地,若X,Y不相关,则有D(X+Y)=D(X)+ D(Y) 切比雪夫不等式的简单应用
3. 协方差及相关系数
协方差:Cov(X ,Y )= E{(X-E(X))(Y-E(Y))}
相关系数:m=Cov(x,y)/√D(X) √D(Y)
当相关系数等于0时,X,Y 不相关,Cov(X ,Y )等于0 不相关不一定独立,但独立一定不相关
-
概率论知识点总结
标规划的数学模型”概念需要看;“解目标规划的图解法”要求掌握;“解目标规划的单纯形法”需要看(第四章)概率论知识点总结第一章一、事…
-
概率论知识点总结
第一章随机事件及其概率第一节基本概念随机实验:将一切具有下面三个特点:(1)可重复性(2)多结果性(3)不确定性的试验或观察称为随…
-
概率论与数理统计知识点总结(详细)
概率论与数理统计第一章概率论的基本概念2样本空间随机事件1事件间的关系AB则称事件B包含事件A指事件A发生必然导致事件B发生ABx…
-
概率论知识点总结及心得体会
概率论总结及心得体会20xx211208班08211106号史永涛班内序号01目录一前五章总结第一章随机事件和概率1第二章随机变量…
-
概率论与数理统计复习资料知识点总结
版权所有未经允许请勿翻印概率论与数理统计第一章随机事件与概率1事件的关系ABABABABAAB2运算规则1ABBAABBAABCA…
-
高中数学知识点总结_第十一、二章概率与统计
高中数学第十一章-概率考试内容:随机事件的概率.等可能性事件的概率.互斥事件有一个发生的概率.相互独立事件同时发生的概率.独立重复…
-
高中数学知识点总结_概率及其应用
概率及其应用1.解概率应用题要学会“说”:首先是记事件,其次是对事件做必要的分析,指出事件的概率类型,包括“等可能性事件”、“互斥…
-
高考概率知识点总结大全
例11(20xx高考江苏2)一个骰子连续投2次,点数和为4的概率.点数和为4,即?1,3?,?2,2?,?3,1?,基本事件的总数…
-
高中数学概率统计知识点总结
一、抽样方法1.简单随机抽样2.简单随机抽样常用的方法:(1)抽签法;⑵随机数表法。3.系统抽样:K(抽样距离)=N(总体规模)/…
-
高中数学知识点总结_概率与统计
概率与统计1.离散型随机变量ξ取每一个值xi(i=1,2,…)的概率为P(??xi)?pi,则P1+P2+…=1;期望是反映随机变…
-
概率论知识点总结
概率论与数理统计期末知识点小结第一章概率论的基本概念1.随机试验确定性现象:在自然界中一定发生的现象称为确定性现象。随机现象:在个…