北京高考数学线性规划题型总结
20##年北京高考线性规划归类解析
 线性规划问题是解析几何的重点,每年高考必有一道小题。
线性规划问题是解析几何的重点,每年高考必有一道小题。
一、已知线性约束条件,探求线性目标关系最值问题
例1、设变量x、y满足约束条件 ,则
,则 的最大值为 。
的最大值为 。
解析:如图1,画出可行域,得在直线2x-y=2与直线x-y=-1的交点A(3,4)处,目标函数z最大值为18
点评:本题主要考查线性规划问题,由线性约束条件画出可行域,然后求出目标函数的最大值.,是一道较为简单的送分题。数形结合是数学思想的重要手段之一。
二、已知线性约束条件,探求非线性目标关系最值问题
 例2、已知
例2、已知 则
则 的最小值是 .
的最小值是 .
解析:如图2,只要画出满足约束条件的可行域,而 表示可行域内一点到原点的距离的平方。由图易知A(1,2)是满足条件的最优解。
表示可行域内一点到原点的距离的平方。由图易知A(1,2)是满足条件的最优解。 的最小值是为5。
的最小值是为5。
点评:本题属非线性规划最优解问题。求解关键是在挖掘目标关系几何意义的前提下,作出可行域,寻求最优解。
三、约束条件设计参数形式,考查目标函数最值范围问题。
 例3、在约束条件
例3、在约束条件 下,当
下,当 时,目标函数
时,目标函数
 的最大值的变化范围是()
的最大值的变化范围是()
A. B.
B.  C.
C.  D.
D. 
解析:画出可行域如图3所示,当 时, 目标函数
时, 目标函数 在
在 处取得最大值, 即
处取得最大值, 即 ;当
;当 时, 目标函数
时, 目标函数 在点
在点 处取得最大值,即
处取得最大值,即 ,故
,故 ,从而选D;
,从而选D;
点评:本题设计有新意,作出可行域,寻求最优解条件,然后转化为目标函数Z关于S的函数关系是求解的关键。
四、已知平面区域,逆向考查约束条件。
 例4、已知双曲线
例4、已知双曲线 的两条渐近线与直线
的两条渐近线与直线 围成一个三角形区域,表示该区域的不等式组是()
围成一个三角形区域,表示该区域的不等式组是()
(A) (B)
(B) (C)
(C)  (D)
(D) 
解析:双曲线 的两条渐近线方程为
的两条渐近线方程为 ,与直线
,与直线 围成一个三角形区域(如图4所示)时有
围成一个三角形区域(如图4所示)时有 。
。
点评:本题考查双曲线的渐近线方程以及线性规划问题。验证法或排除法是最效的方法。
五、已知最优解成立条件,探求目标函数参数范围问题。
 例5已知变量
例5已知变量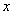 ,
, 满足约束条件
满足约束条件 。若目标函数
。若目标函数 (其中
(其中 )仅在点
)仅在点 处取得最大值,则
处取得最大值,则 的取值范围为 。
的取值范围为 。
解析:如图5作出可行域,由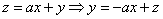 其表示为斜率为
其表示为斜率为 ,纵截距为z的平行直线系, 要使目标函数
,纵截距为z的平行直线系, 要使目标函数 (其中
(其中 )仅在点
)仅在点 处取得最大值。则直线
处取得最大值。则直线 过A点且在直线
过A点且在直线 (不含界线)之间。即
(不含界线)之间。即 则
则 的取值范围为
的取值范围为 。
。
点评:本题通过作出可行域,在挖掘 的几何意义的条件下,借助用数形结合利用各直线间的斜率变化关系,建立满足题设条件的
的几何意义的条件下,借助用数形结合利用各直线间的斜率变化关系,建立满足题设条件的 的不等式组即可求解。求解本题需要较强的基本功,同时对几何动态问题的能力要求较高。
的不等式组即可求解。求解本题需要较强的基本功,同时对几何动态问题的能力要求较高。
 六、设计线性规划,探求平面区域的面积问题
六、设计线性规划,探求平面区域的面积问题
例6在平面直角坐标系中,不等式组 表示的平面区域的面积是()(A)
表示的平面区域的面积是()(A) (B)4 (C)
(B)4 (C)  (D)2
(D)2
解析:如图6,作出可行域,易知不等式组 表示的平面区域是一个三角形。容易求三角形的三个顶点坐标为A(0,2),B(2,0),C(-2,0).于是三角形的面积为:
表示的平面区域是一个三角形。容易求三角形的三个顶点坐标为A(0,2),B(2,0),C(-2,0).于是三角形的面积为: 从而选B。
从而选B。
点评:有关平面区域的面积问题,首先作出可行域,探求平面区域图形的性质;其次利用面积公式整体或部分求解是关键。
七、研究线性规划中的整点最优解问题
 例7、某公司招收男职员x名,女职员y名,x和y须满足约束条件
例7、某公司招收男职员x名,女职员y名,x和y须满足约束条件 则
则 的最大值是(A)80 (B) 85 (C) 90 (D)95
的最大值是(A)80 (B) 85 (C) 90 (D)95
解析:如图7,作出可行域,由 ,它表示为斜率为
,它表示为斜率为 ,纵截距为
,纵截距为 的平行直线系,要使
的平行直线系,要使 最得最大值。当直线
最得最大值。当直线 通过
通过
 取得最大值。因为
取得最大值。因为 ,故A点不是最优整数解。于是考虑可行域内A点附近整点B(5,4),C(4,4),经检验直线经过B点时,
,故A点不是最优整数解。于是考虑可行域内A点附近整点B(5,4),C(4,4),经检验直线经过B点时,
点评:在解决简单线性规划中的最优整数解时,可在去掉限制条件求得的最优解的基础上,调整优解法,通过分类讨论获得最优整数解。
第二篇:高中数学等差数列题型总结
一、等差数列
1、数列的概念
例1.根据数列前4项,写出它的通项公式:
(1)1,3,5,7……;(2)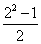 ,
, ,
, ,
,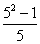 ;(3)
;(3) ,
,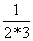 ,
,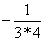 ,
,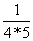 。
。
解析:(1)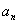 =2
=2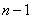 ; (2)
; (2)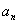 =
= 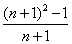 ; (3)
; (3)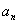 =
= 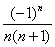 。
。
如(1)已知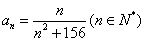 ,则在数列
,则在数列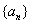 的最大项为__ ;
的最大项为__ ;
(2)数列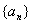 的通项为
的通项为 ,其中
,其中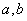 均为正数,则
均为正数,则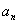 与
与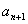 的大小关系为___;
的大小关系为___;
(3)已知数列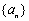 中,
中,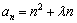 ,且
,且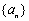 是递增数列,求实数
是递增数列,求实数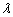 的取值范围;
的取值范围;
2、等差数列的判断方法:定义法 或
或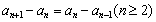 。
。
例2.设Sn是数列{an}的前n项和,且Sn=n2,则{an}是( )
A.等比数列,但不是等差数列 B.等差数列,但不是等比数列
C.等差数列,而且也是等比数列 D.既非等比数列又非等差数列
答案:B;解法一:an=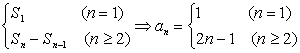 ,∴an=2n-1(n∈N)
,∴an=2n-1(n∈N)
又an+1-an=2为常数,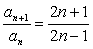 ≠常数,∴{an}是等差数列,但不是等比数列.
≠常数,∴{an}是等差数列,但不是等比数列.
解法二:如果一个数列的和是一个没有常数项的关于n的二次函数,则这个数列一定是等差数列。
练一练:设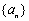 是等差数列,求证:以bn=
是等差数列,求证:以bn=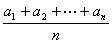
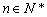 为通项公式的数列
为通项公式的数列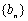 为等差数列。
为等差数列。
3、等差数列的通项: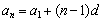 或
或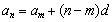 。
。
4、等差数列的前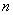 和:
和: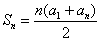 ,
,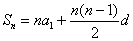 。
。
例3:等差数列{an}的前n项和记为Sn,若a2+a4+a15的值是一个确定的常数,则数列{an}中也为常数的项是( )
A.S7 B.S8 C.S13 D.S15
解析:设a2+a4+a15=p(常数),∴3a1+18d=p,解a7=p.∴S13==13a7=p. 答案:C
例4.等差数列{an}中,已知a1=,a2+a5=4,an=33,则n为( )
A.48 B.49 C.50 D.51
解析:∵a2+a5=2a1+5d=4,则由a1=得d=,令an=33=+(n-1)×,可解得n=50.故选C.
如(1)等差数列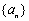 中,
中, ,
,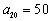 ,则通项
,则通项 ;
;
(2)首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是______ ;
例5:设Sn是等差数列{an}的前n项和,a12=-8,S9=-9,则S16=________.
解析:S9=9a5=-9,∴a5=-1,S16=8(a5+a12)=-72. 答案:-72
例6:已知数列{an}为等差数列,若<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为( )
A.11 B.19 C.20 D.21
解析:∵<-1,且Sn有最大值,∴a10>0,a11<0,且a10+a11<0,∴S19==19·a10>0,S20==10(a10+a11)<0.
所以使得Sn>0的n的最大值为19,故选B.答案:B
如(1)数列 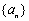 中,
中,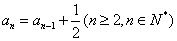 ,
, ,前n项和
,前n项和 ,则
,则 =_,
=_,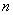 = ;
= ;
(2)已知数列 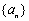 的前n项和
的前n项和 ,求数列
,求数列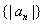 的前
的前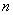 项和
项和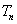 .
.
5、等差中项:若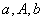 成等差数列,则A叫做
成等差数列,则A叫做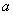 与
与 的等差中项,且
的等差中项,且 。
。
提醒:(1)等差数列的通项公式及前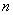 和公式中,涉及到5个元素:
和公式中,涉及到5个元素: 、
、 、
、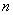 、
、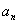 及
及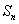 ,其中
,其中 、
、 称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
(2)为减少运算量,要注意设元的技巧,如奇数个数成等差,可设为…,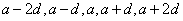 …(公差为
…(公差为 );偶数个数成等差,可设为…,
);偶数个数成等差,可设为…,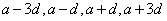 ,…(公差为2
,…(公差为2 )
)
6.等差数列的性质:
常用结论
(1)前n项和为 ,则
,则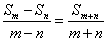 (m、n∈N*,且m≠n)。
(m、n∈N*,且m≠n)。
(2)若m+n=p+q(m、n、p、q∈N*,且m≠n,p≠q),则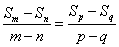 。
。
(3)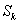 ,
,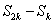 ,
,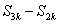 成等差数列。
成等差数列。
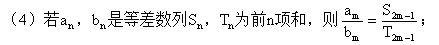
即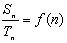 ,则
,则
(5) ①若a1>0,d<0, 有最大值,可由不等式组
有最大值,可由不等式组 来确定n;
来确定n;
②若a1<0,d>0, 有最小值,可由不等式组
有最小值,可由不等式组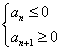 来确定n,也可由前n项和公式
来确定n,也可由前n项和公式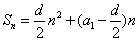 来确定n。
来确定n。
(6)若an=m,am=n, (m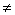 n)则am+n=0
n)则am+n=0
(7)若an=m,am=n, (m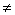 n)则am+n=0
n)则am+n=0
(8)若Sn=m,Sm=n, (m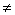 n)则Sm+n=—m—n
n)则Sm+n=—m—n
重点:
(1)当公差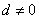 时,等差数列的通项公式
时,等差数列的通项公式 是关于
是关于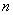 的一次函数,且斜率为公差
的一次函数,且斜率为公差 ;前
;前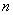 和
和 是关于
是关于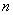 的二次函数且常数项为0.
的二次函数且常数项为0.
(2)若公差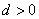 ,则为递增等差数列,若公差
,则为递增等差数列,若公差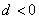 ,则为递减等差数列,若公差
,则为递减等差数列,若公差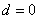 ,则为常数列。
,则为常数列。
(3)当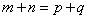 时,则有
时,则有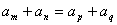 ,特别地,当
,特别地,当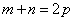 时,则有
时,则有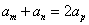 .
.
(4)若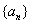 、
、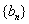 是等差数列,则
是等差数列,则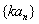 、
、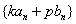 (
( 、
、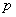 是非零常数)、
是非零常数)、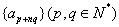 、
、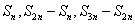 ,…也成等差数列,而
,…也成等差数列,而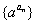 成等比数列;若
成等比数列;若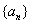 是等比数列,且
是等比数列,且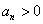 ,则
,则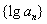 是等差数列.
是等差数列.
练一练:等差数列的前n项和为25,前2n项和为100,则它的前3n和为 。
(5)在等差数列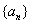 中,当项数为偶数
中,当项数为偶数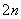 时,
时,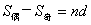 ;项数为奇数
;项数为奇数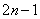 时,
时,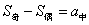 ,
,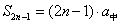 (这里
(这里 即
即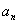 );
);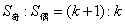 。
。
练一练:项数为奇数的等差数列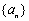 中,奇数项和为80,偶数项和为75,求此数列的中间项与项数.
中,奇数项和为80,偶数项和为75,求此数列的中间项与项数.
(6)若等差数列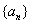 、
、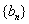 的前
的前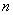 和分别为
和分别为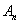 、
、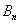 ,且
,且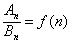 ,则
,则 .
.
练一练:设{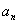 }与{
}与{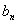 }是两个等差数列,它们的前
}是两个等差数列,它们的前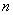 项和分别为
项和分别为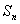 和
和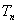 ,若
,若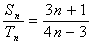 ,那么
,那么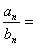 ___________;
___________;
(7)“首正”的递减等差数列中,前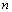 项和的最大值是所有非负项之和;“首负”的递增等差数列中,前
项和的最大值是所有非负项之和;“首负”的递增等差数列中,前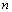 项和的最小值是所有非正项之和。法一:由不等式组
项和的最小值是所有非正项之和。法一:由不等式组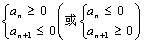 确定出前多少项为非负(或非正);法二:因等差数列前
确定出前多少项为非负(或非正);法二:因等差数列前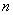 项是关于
项是关于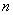 的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性
的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性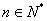 。上述两种方法是运用了哪种数学思想?(函数思想),由此你能求一般数列中的最大或最小项吗?
。上述两种方法是运用了哪种数学思想?(函数思想),由此你能求一般数列中的最大或最小项吗?
练一练:等差数列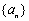 中,
中,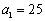 ,
,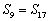 ,问此数列前多少项和最大?并求此最大值;
,问此数列前多少项和最大?并求此最大值;
例7.(1)设{an}(n∈N*)是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
A.d<0 B.a7=0 C.S9>S5 D.S6与S7均为Sn的最大值
(2)等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为( )
A.130 B.170 C.210 D.260
解析:(1)答案:C;由S5<S6得a1+a2+a3+…+a5<a1+a2+…+a5+a6,∴a6>0,又S6=S7,∴a1+a2+…+a6=a1+a2+…+a6+a7,∴a7=0,
由S7>S8,得a8<0,而C选项S9>S5,即a6+a7+a8+a9>0 2(a7+a8)>0,由题设a7=0,a8<0,显然C选项是错误的。
2(a7+a8)>0,由题设a7=0,a8<0,显然C选项是错误的。
(2)答案:C。解法一:由题意得方程组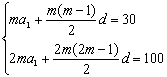 ,视m为已知数,解得
,视m为已知数,解得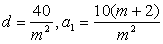 ,
,
∴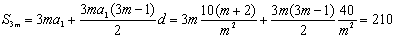 。
。
解法二:设前m项的和为b1,第m+1到2m项之和为b2,第2m+1到3m项之和为b3,则b1,b2,b3也成等差数列。于是b1=30,b2=100-30=70,公差d=70-30=40。∴b3=b2+d=70+40=110,∴前3m项之和S3m=b1+b2+b3=210.
解法三:取m=1,则a1=S1=30,a2=S2-S1=70,从而d=a2-a1=40。于是a3=a2+d=70+40=110.∴S3=a1+a2+a3=210。
等差数列课后练习
一、选择题
1.若a≠b,数列a,x1,x 2 ,b和数列a,y1 ,y2 ,b都是等差数列,则 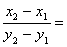 ( )
( )
A.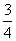 B.
B.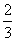 C.1 D.
C.1 D.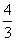
2.在等差数列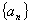 中,公差
中,公差 =1,
=1,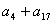 =8,则
=8,则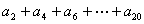 = ( )
= ( )
A.40 B.45 C.50 D.55
3.等差数列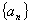 的前三项为
的前三项为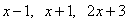 ,则这个数列的通项公式为 ( )
,则这个数列的通项公式为 ( )
A.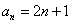 B.
B.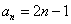 C.
C.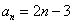 D.
D.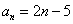
4.在等差数列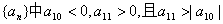 ,则在Sn中最大的负数为 ( )
,则在Sn中最大的负数为 ( )
A.S17 B.S18 C.S19 D.S20
5.已知等差数列的首项为31,若此数列从第16项开始小于1,则此数列的公差d 的取值范围是
A.(-∞,-2) B.[-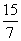 , -2] C.(-2, +∞) D.(—
, -2] C.(-2, +∞) D.(—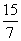 ,-2)
,-2)
6.在等差数列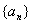 中,若
中,若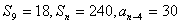 ,则n的值为 ( )
,则n的值为 ( )
A.18 B17. C.16 D.15
7.等差数列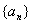 中,
中,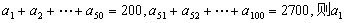 等于( )
等于( )
A.-20.5 B.-21.5 C.-1221 D.-20
8.已知某数列前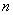 项之和
项之和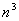 为,且前
为,且前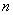 个偶数项的和为
个偶数项的和为 ,则前
,则前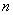 个奇数项的和为
个奇数项的和为
A.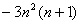 B.
B.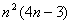 C.
C.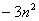 D.
D.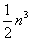
9.一个只有有限项的等差数列,它的前5项的和为34,最后5项的和为146所有项的和为234,则它的第七项等于
A.22 B .21 C.19 D.18
10.等差数列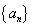 中,
中,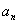
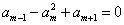 ≠0,若m>1且
≠0,若m>1且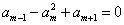 ,
,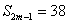 ,则m的值是
,则m的值是
A. 10 B. 19 C.20 D.38
二、填空题
11.已知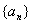 是等差数列,且
是等差数列,且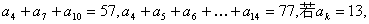 则k= .
则k= .
12.在△ABC中,A,B,C成等差数列,则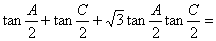 .
.
13.在等差数列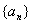 中,若
中,若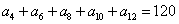 ,则
,则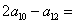 .
.
14.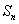 是等差数列
是等差数列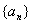 的前n项和,
的前n项和,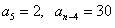 (n≥5,
(n≥5,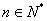 ),
),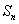 =336,则n的值是 .
=336,则n的值是 .
三、解答题
15.己知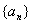 为等差数列,
为等差数列, ,若在每相邻两项之间插入三个数,使它和原数列的数构成一个新的等差数列,求:
,若在每相邻两项之间插入三个数,使它和原数列的数构成一个新的等差数列,求:
(1)原数列的第12项是新数列的第几项? (2)新数列的第29项是原数列的第几项?
16.数列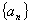 是首项为23,公差为整数的等差数列,且第六项为正,第七项为负。
是首项为23,公差为整数的等差数列,且第六项为正,第七项为负。
(1)求数列公差;(2)求前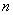 项和
项和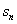 的最大值;(3)当
的最大值;(3)当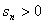 时,求
时,求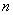 的最大值。
的最大值。
17.设等差数列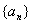 的前n项的和为S n ,且S 4 =-62, S 6 =-75,求:
的前n项的和为S n ,且S 4 =-62, S 6 =-75,求:
(1)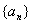 的通项公式a n 及前n项的和S n ; (2)|a 1 |+|a 2 |+|a 3 |+……+|a 14 |.
的通项公式a n 及前n项的和S n ; (2)|a 1 |+|a 2 |+|a 3 |+……+|a 14 |.
18.已知数列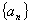 ,首项a 1 =3且2a n+1=S n ·S n-1 (n≥2).
,首项a 1 =3且2a n+1=S n ·S n-1 (n≥2).
(1)求证:{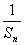 }是等差数列,并求公差;(2)求{a n }的通项公式;
}是等差数列,并求公差;(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
选择题:ABCCB DABDA 填空题:11.8; 12.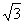 ; 13.24; 14.21.
; 13.24; 14.21.
解答题:15.分析:应找到原数列的第n项是新数列的第几项,即找出新、旧数列的对应关系。解:设新数列为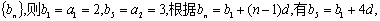 即3=2+4d,∴
即3=2+4d,∴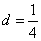 ,∴
,∴ ,
,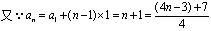 ,∴
,∴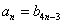 ,即原数列的第n项为新数列的第4n-3项.(1)当n=12时,4n-3=4×12-3=45,故原数列的第12项为新数列的第45项;(2)由4n-3=29,得n=8,故新数列的第29项是原数列的第8项。
,即原数列的第n项为新数列的第4n-3项.(1)当n=12时,4n-3=4×12-3=45,故原数列的第12项为新数列的第45项;(2)由4n-3=29,得n=8,故新数列的第29项是原数列的第8项。
说明:一般地,在公差为d的等差数列每相邻两项之间插入m个数,构成一个新的等差数列,则新数列的公差为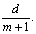 原数列的第n项是新数列的第n+(n-1)m=(m+1)n-m项.
原数列的第n项是新数列的第n+(n-1)m=(m+1)n-m项.
16.解: (1)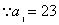 ,
, 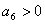 ,
,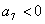 , ∴
, ∴ 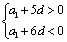
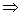
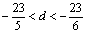
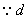 为整数, ∴
为整数, ∴ 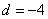 .
.
(2)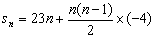 =23
=23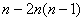 =-2
=-2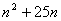 =-
=-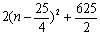 ,∴当
,∴当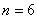 时
时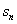 最大=78
最大=78
(3)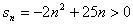 时,0
时,0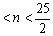 ,故
,故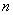 最大值为12.
最大值为12.
17.解:设等差数列首项为a1,公差为d,依题意得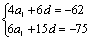 ,解得:a1=-20,d=3。⑴
,解得:a1=-20,d=3。⑴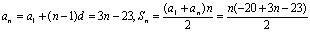
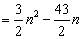 ⑵
⑵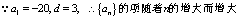
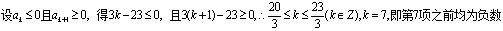 ∴
∴
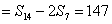 .
.
18.分析:证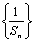 为等差数列,即证
为等差数列,即证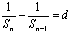 (d是常数)。解:⑴由已知当
(d是常数)。解:⑴由已知当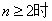
 ⑵
⑵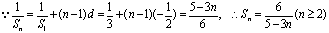
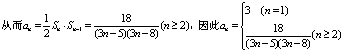
⑶
-
高考数学题型归纳完整版
第一章集合与常用逻辑用语第一节集合题型1-1集合的基本概念题型1-2集合间的基本关系题型1-3集合的运算第二节命题及其关系、充分条…
-
高中数学题型总结
不等式题型总结典题精讲例11已知0x2求函数yx1x13求函数yx13x的最大值的值域思路分析1由极值定理可知需构造某个和为定值可…
-
高考数学题型总结与分析
高考数学题型总结与分析专题一集合与常用逻辑用语1集合的基本概念2集合的基本关系运算与创新性问题3四种命题及其相互关系4充要条件的判…
-
20xx高考数学题型归纳
20xx高考数学题型归纳圆锥曲线1直线与圆锥曲线的位置关系要解决直线与圆锥曲线的位置关系问题通常把直线方程与圆锥曲线方程联立消去y…
-
1高考数学导数题型归纳( 好)
导数题型归纳请同学们高度重视首先关于二次函数的不等式恒成立的主要解法1分离变量2变更主元3根分布4判别式法5二次函数区间最值求法1…
-
20xx高考圆锥曲线知识点总结
学而通黄冈教育学生李元龙圆锥曲线知识总结一圆锥曲线定义椭圆平面内与两个定点椭圆这两个定点数学语言常数2a轨迹是线段2a的距离之和等…
-
高考圆锥曲线最经典题型总结
高考圆锥曲线最经典题型总结第一定义第二定义双曲线渐近线等考查120xx辽宁理数设双曲线的个焦点为F虚轴的个端点为B如果直线FB与该…
-
20xx年高考数学专题复习 椭圆与双曲线的性质 完整归纳
20xx年高考专题复习椭圆与双曲线的性质椭圆1PF1PF22ax2y22标准方程221abPF13e1d14点P处的切线PT平分P…
-
【名师名校典型题】20xx高考数学二轮复习名师知识点总结:圆锥曲线中的热点问题
圆锥曲线中的热点问题1本部分主要以解答题形式考查往往是试卷的压轴题之一一般以椭圆或抛物线为背景考查弦长定点定值最值范围问题或探索性…
-
20xx年高考双曲线知识点归纳及高考试题附详细答案
20xx年高考双曲线知识点归纳及高考试题附详细答案1双曲线的定义第一定义平面内到两个定点F1F2的距离之差的绝对值等于定值2a0l…
-
优质服务窗口个人总结000
提升个人素质争创群众满意服务员根据组织安排,20xx年我到行政审批服务中心负责计划生育事项行政审批工作。一年来,在中心领导和计生委…