我的矩阵分析总结
矩阵分析期末复习
1. 判断一个集合是否为线性空间
只需要验证2条:加法封闭性; 乘法封闭性
例:
1)
2)
3) 
2. 判断一组基是否为标准正交基
验证2条:各个向量的模是否为1; 两两向量内积是否为0
例:a1 = (0,1,0), a2 = (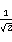 , 0,
, 0, 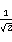 ),a3 = (
),a3 = (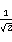 , 0,
, 0, )
)
构成R3的一个标准正交基,因为:
| a1 | = | a2 | = | a3 | = 1
< a1 , a2> = < a1 , a3 > = < a2 , a3 > = 0
3. 求一个线性变换的核T-1(0)、象集T(V)
例:
(1)证明T(x1, x2, … ,xn) = (0, x1, x2, …, xn-1)是线性空间Pn的线性变换且Tn = 0 (零变换).
(2)求T的核T-1(0)的维数、象集T(V)的维数
证明:
(1) 由线性变换的定义,易证T是线性变换,又因
T2(x1, x2, … ,xn)
= T(0, x1, x2, …, xn-1)
= (0, 0, x1, x2, …, xn-2)
…
= Tn(x1, x2, … ,xn) = (0, 0, …, 0)
即Tn = 0(零变换)
(2) 若T(x1, x2, … ,xn) = (0, x1, x2, …, xn-1) = (0, 0, …, 0)
则x1 = x2 = … = xn-1 = 0.
即T-1(0)为由一切形如(0, 0, …, xn)的向量构成的子空间,它是一维子空间,(0, 0, …, 1)是它的基。
4. 用最小二乘法解方程组
例:用最小二乘法解下列方程组
 x1+x2 = 1
x1+x2 = 1
x1+x3 = 2
x1+x2+x3 = 0
x1 +2x2 – x3 = -1
解:
系数矩阵A =  ,其转置AT =
,其转置AT =  ,B =
,B = 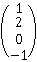
利用公式ATAX = ATB,有
ATAX = 
 =
= = ATB
= ATB
于是求得最小二乘解为:
x1 =  , x2 = -
, x2 = -  , x3 = -
, x3 = - 
5. 求矩阵的史密斯标准型
初等行、列变换
例:求多项式矩阵A( λ ) =  的史密斯标准形
的史密斯标准形
答案:d1(λ) =1,d2(λ) =λ, d3(λ) =λ(λ-1)( λ-2)
6. 求矩阵的约当标准形
例:求矩阵A的约当标准形,其中
A = 
step1:先求矩阵A的史密斯标准形;
step2:再写出不变因子、初级因子,令初级因子等于0,求解;
step3:最后写出约当标准形.
7. 判断一个矩阵级数是否收敛
方法一:用矩阵的谱半径来判断
方法二:当谱半径失效时,用约当标准型来判断
8. 求带参数的矩阵函数
9. 向量的范数、矩阵的范数
向量的范数:
例:x = (1, -2, 3)T
║x║1 = |1| + |-2| + |3| = 1 + 2 + 3 = 6
║x║2 = (|1|2 + |-2|2 + |3|2)1/2 = (1 + 4 + 9) 1/2 = 
║x║ = max(|1|, |-2|, |3|) = max(1, 2, 3) = 3
= max(|1|, |-2|, |3|) = max(1, 2, 3) = 3
矩阵的范数:
例:A = 
║A║1 = max(|1|+|-1|+|0|,|2|+|2|+|1|,|0|+|-1|+|1|) = max(2, 5, 2)= 5 列和范数
║A║ = max(|1|+|2|+|0|,|-1|+|2|+|-1|,|0|+|1|+|1|) = max(3, 4, 2)= 4 行和范数
= max(|1|+|2|+|0|,|-1|+|2|+|-1|,|0|+|1|+|1|) = max(3, 4, 2)= 4 行和范数
║A║2= max (AHA) 谱范数
(AHA) 谱范数
AHA = 
 =
= 
特征方程为:λE - AHA =  = 0
= 0
得 λ1 = 9.1428 , λ2 = 2.9211, λ3 = 0.9361
所以║A║2 =  = 3.0237
= 3.0237
║A║F = (12+22+0+(-1)2+22+(-1)2+0+12+12) = 1 + 4 + 1 + 4 + 1 + 1 + 1 = 13
10. 利用盖尔圆盘定理求特征值的取值范围
例:估计矩阵A =  的特征值范围.
的特征值范围.
解:圆盘定理所指的四个圆盘为:
|z-1|≤ 0.1 + 0.2 + 0.3 = 0.6
|z-3|≤ 0.5 + 0.1 + 0.2 = 0.8
|z+1|≤ 1 + 0.3 + 0.5 = 1.8
|z+4|≤ 0.2 + 0.3 + 0.1 = 0.6
11. 求广义逆A+(行满秩、列满秩)
例:求A =  的广义M-P逆矩阵。
的广义M-P逆矩阵。
第二篇:矩阵分析课程总结






-
特殊矩阵总结
特殊矩阵总结常用的产生通用特殊矩阵的函数有zeros产生全0矩阵零矩阵ones产生全1矩阵幺矩阵eye产生单位矩阵rand产生01…
-
我的矩阵分析总结
矩阵分析期末复习1判断一个集合是否为线性空间只需要验证2条加法封闭性乘法封闭性例1Sx1x2x3x1x2x301234142Sxx…
-
矩阵论小结
矩阵论线性空间定义本质是个集合满足一定条件下的集合首先定义了加法运算满足加法的交换结合律在这个集合中能找到零元素与负元素然后定义数…
-
矩阵理论考试总结
1向量矩阵是一个严密的数学概念数组是计算机上的一个名词一组数而已非要赋予数组数学含义则一维数组相当于向量二维数组相当于矩阵矩阵是数…
-
矩阵解题总结
矩阵解题总结迄今我们都做了不少的矩阵习题我们常常以刷题来满足自己的做题欲望并以此方法来让自己对矩阵这个新概念有更好的了解那么在我们…
-
矩阵式管理优缺点总结
目前,受国际管理新理念的影响,一种交叉、双向的管理模式已经在越来越多的公司开始运用,它就是矩阵式管理,采用这种管理模式的企业,在构…
-
采油厂矩阵培训工作总结 -
剖析基层培训现状强化直线培训责任树立需求培训理念------采油二厂矩阵培训工作总结一、采油二厂情况简介:青海油田公司采油二厂成立…
-
科研训练总结 研究矩阵理论
科研训练总结数学科学学院柏慧荣2910102024本学期我参加了学院组织的科研训练讨论课,我参与的方向主要是研究矩阵理论。虽然上课…
-
特殊矩阵总结
特殊矩阵总结常用的产生通用特殊矩阵的函数有zeros产生全0矩阵零矩阵ones产生全1矩阵幺矩阵eye产生单位矩阵rand产生01…
-
矩阵论小结
矩阵论线性空间定义本质是个集合满足一定条件下的集合首先定义了加法运算满足加法的交换结合律在这个集合中能找到零元素与负元素然后定义数…