酉矩阵与HERMITE矩阵性质总结
酉矩阵与Hermite矩阵的浅谈
韦龙 201131402
摘要
科学在发展,社会在进步,人们对于数学的理解越来越深刻,数学应用于日常生活生产越来越广泛。在数学的很多分支和工程实际应用中, 都涉及到一些特殊的矩阵的性质及构造. 本文讨论两类特殊的矩阵——酉矩阵和Hermite矩阵. 酉矩阵和Hermite矩阵作为两类特殊的矩阵, 有很多良好的性质, 在矩阵理论中具有举足轻重的作用。本文通过对正交矩阵和酉矩阵关系的概述、酉矩阵的性质和酉矩阵的构造来初步认识酉矩阵,为以后的深入学习奠定基础。本文主要从Hermite矩阵的性质,判定定理,正定性和Hermite矩阵不等式四个方面讨论Hermite矩阵。
关键词: 酉矩阵;Hermite矩阵;正交矩阵;特征值。
The study of Unitary matrix and Hermite matrix
Wei Long 201131402
Abstract
With the development of science and society, people get a deeper understanding of math , and the use of math becomes more and more widely. In many branches of mathematics and engineering applications, are related to some special nature and structure matrix. This paper discusses a special kind of matrix - unitary matrix and Hermite matrix. The two kinds of matrix as two specials kind of matrix, there are many good properties. In the matrix theory plays an important role in the study of this topic could be more perfect matrix theory. In this paper , we use the knowledge of the unitary matrix and Orthogonal matrix ,the nature of the unitary matrix, the construction of the unitary matrix to get a first impression of the unitary matrix, and make a basement to farther study. And we study the Hermite matrix by the knowledge of the nature of Hermite matrix,determined theorem ,positive definite matrix and the Hermite matrix inequality.
Key words: unitary matrix ;Hermite matrix ;Orthogonal matrix; Characteristic value
第一章 酉矩阵
第一节 酉矩阵的概念及等价条件
1.1.1 正交矩阵和酉矩阵
定义1.1.1 满足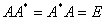 的
的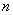 阶实矩阵
阶实矩阵 称为正交矩阵.
称为正交矩阵.
在矩阵理论中, 经常利用矩阵来描述变换. 在实空间中正交变换保持度量不变, 而正交变换中对应的变换矩阵就是正交矩阵, 所以对正交矩阵的研究就显得格外重要. 同样道理, 想要得到复空间中保持度量不变的线性变换, 就应该对正交变换进行推广, 将其推广到复数域上, 那对应的正交矩阵相应的也推广到复数域就是酉矩阵.
1.1.2 酉矩阵的等价条件
先给出酉矩阵的以下定义.
定义1.1.2若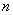 阶复方阵
阶复方阵 满足
满足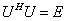 则称
则称 为酉矩阵.
为酉矩阵.
定义1.1.3 若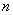 阶复方阵
阶复方阵 满足
满足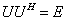 则称
则称 为酉矩阵.
为酉矩阵.
定义1.1.4若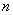 阶复方阵
阶复方阵 满足
满足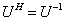 则称
则称 为酉矩阵.
为酉矩阵.
注: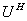 表示矩阵
表示矩阵 的共轭转置,即
的共轭转置,即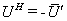 .
.
定义1.1.5若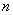 阶复方阵
阶复方阵 的
的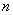 个行(列)向量是两两正交的单位向量, 则称
个行(列)向量是两两正交的单位向量, 则称 为酉矩阵.
为酉矩阵.
易知定义1.1.2—定义1.1.5是相互等价的. 从定义1.1.2或定义1.1.3或定义1.1.4知,酉矩阵是可逆矩阵.根据定义1.1.5可得, 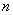 阶酉矩阵
阶酉矩阵 的
的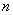 个行(列)向量构成
个行(列)向量构成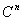 的标准正交基.
的标准正交基.
引理1.1.1[3] 酉矩阵的行列式的模为1
引理1.1.2[4] 对任意的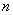 阶矩阵
阶矩阵 有
有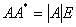 .
.
引理1.1.3[5] 对任意的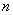 阶矩阵
阶矩阵 和
和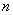 阶可逆矩阵
阶可逆矩阵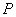 , 有
, 有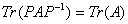
引理1.1.4[6] 对任意的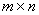 阶矩阵
阶矩阵 和
和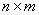 阶矩阵
阶矩阵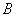 , 有
, 有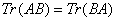
引理1.1.5[6]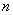 阶矩阵
阶矩阵 为酉矩阵的充分必要条件是:
为酉矩阵的充分必要条件是: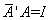 或者
或者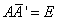
定理1.1.1阵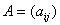 为酉矩阵的充分必要条件是
为酉矩阵的充分必要条件是
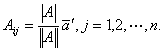
这里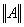 表示行列
表示行列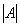 的模, 表示
的模, 表示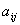 的共轭复数.
的共轭复数.
定理1.1.2 二阶矩阵 为酉矩阵的充分必要条件是
为酉矩阵的充分必要条件是 为下列三种形式之一 :
为下列三种形式之一 :
(i) 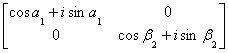
(ii) 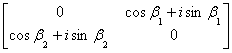
(iii) 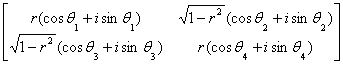
这里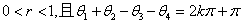 ,
,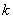 为整数.
为整数.
定理1.1.3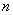 阶矩阵
阶矩阵 为酉矩阵的充要条件是: 对任意
为酉矩阵的充要条件是: 对任意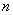 阶矩阵B, 有:
阶矩阵B, 有:
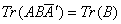
第二节 酉矩阵的性质
1.2.1 运算性质
1.2.1 酉矩阵的转置与伴随矩阵
定理1.2.1 设 为酉矩阵,则
为酉矩阵,则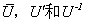 都是酉矩阵.
都是酉矩阵.
证明因为
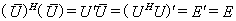
所以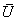 是酉矩阵.
是酉矩阵.
因为
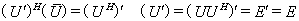
所以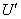 是酉矩阵.
是酉矩阵.
因为
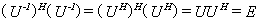
所以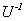 是酉矩阵.
是酉矩阵.
定理1.2.2 设 为酉矩阵, 则
为酉矩阵, 则 的伴随矩阵
的伴随矩阵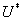 也是酉矩阵.
也是酉矩阵.
证明 因为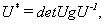
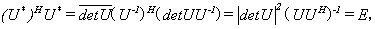
所以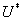 为酉矩阵.
为酉矩阵.
定理1.2.3 设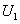 和
和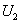 是酉矩阵,则
是酉矩阵,则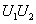 ,
, 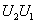 也是酉矩阵.
也是酉矩阵.
证明 因为
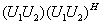
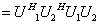
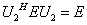
所以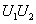 是酉矩阵, 同理可证,
是酉矩阵, 同理可证,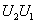 也是酉矩阵.
也是酉矩阵.
推论1.2.1 设 是酉矩阵,则
是酉矩阵,则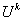 (
(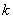 为正整数)是酉矩阵.
为正整数)是酉矩阵.
推论1.2.2 设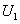 ,
,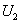 是酉矩阵,则
是酉矩阵,则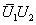 ,
,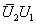 ;
;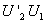 ,
,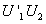 ;
;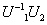 ,
,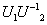 ;
;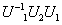 ,
,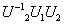 也是酉矩阵.
也是酉矩阵.
推论1.2.3 设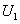 ,
,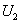 是酉矩阵,则
是酉矩阵,则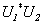 ,
,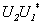 也是酉矩阵.
也是酉矩阵.
推论1.2.4 设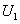 ,
,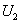 是酉矩阵,则
是酉矩阵,则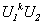 ,
,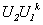 ,
,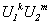 (
(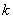 ,
, 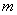 为正整数)也是酉矩阵.
为正整数)也是酉矩阵.
定理1.2.4 设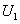 ,
,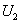 是酉矩阵,若
是酉矩阵,若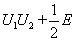 是反
是反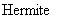 矩阵, 则
矩阵, 则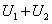 也是酉矩阵, 因此
也是酉矩阵, 因此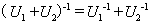
证明 因为
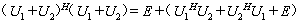
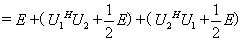
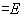
因此,当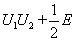 是是反
是是反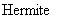 矩阵时,
矩阵时, 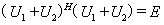 ,记
,记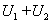 也是酉矩阵,从而
也是酉矩阵,从而
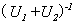
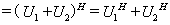
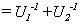
注: 定理2.4表明, 酉矩阵的和未必是酉矩阵.
1.2.2 酉矩阵的行列式
定理1.2.5 设 是酉矩阵,则其行列式的模等于1,即
是酉矩阵,则其行列式的模等于1,即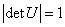 ,其中
,其中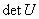 表示
表示 的行列式.
的行列式.
证明 由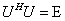 得
得
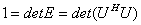
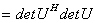
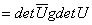
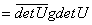
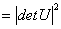
从而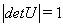 .
.
定理1.2.6 设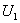 ,
, 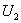 是酉矩阵,则
是酉矩阵,则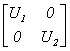 ,
,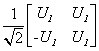 也是酉矩阵.
也是酉矩阵.
证明 因为
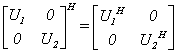
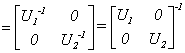
所以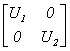 是酉矩阵.
是酉矩阵.
因为
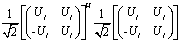
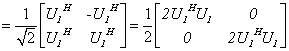
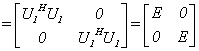
所以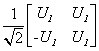 是酉矩阵.
是酉矩阵.
定理1.2.7 设 是酉矩阵, 则对
是酉矩阵, 则对 的任一行(列)乘以模为1的数或任两行(列)互换, 所得矩阵仍为酉矩阵.
的任一行(列)乘以模为1的数或任两行(列)互换, 所得矩阵仍为酉矩阵.
证明 设
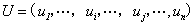
其中
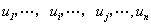
是 的两两正交单位向量.
的两两正交单位向量.
显然
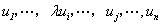 (
(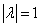 )
)
以及
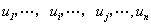
也都是 的两两正交的单位向量. 由定义1.1.5知结论成立.
的两两正交的单位向量. 由定义1.1.5知结论成立.
1.2.3 酉矩阵的特征值与对角化
定理1.2.8设 是酉矩阵, 则
是酉矩阵, 则 的特征值的模为1, 即分布在复平面的单位圆上.
的特征值的模为1, 即分布在复平面的单位圆上.
证明 设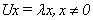 , 则由
, 则由
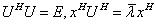
可得
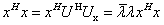
于是
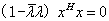
而
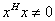 , 故
, 故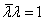
即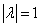
定理1.2.9设 为酉矩阵,
为酉矩阵, 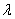 是
是 的特征值, 则
的特征值, 则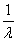 是
是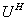 的特征值, 而
的特征值, 而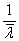 是
是 的特征值.
的特征值.
证明 设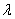 是
是 的特征值, 则由定理1.2.1知
的特征值, 则由定理1.2.1知
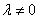
于是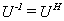 的特征值, 而又可知
的特征值, 而又可知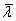 是
是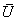 的特征值, 但
的特征值, 但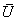 与
与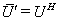 的特征值全部相同,因此
的特征值全部相同,因此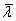 是
是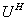 的特征值, 所以
的特征值, 所以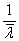 是
是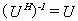 的特征值.
的特征值.
定理1.2.10设 是酉矩阵, 则属于
是酉矩阵, 则属于 的不同特征值的特征向量正交.
的不同特征值的特征向量正交.
证明设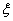 是
是 的属于特征值
的属于特征值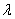 的特征向量,
的特征向量, 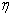 是
是 的属于特征值
的属于特征值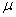 的特征向量, 由
的特征向量, 由
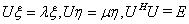
可得
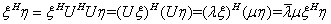
所以
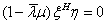
而
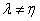
从而
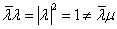
故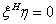 , 即
, 即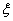 与
与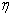 正交.
正交.
定理1.2.11设 是酉矩阵, 且为
是酉矩阵, 且为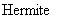 矩阵, 则
矩阵, 则 必为对合矩阵
必为对合矩阵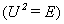 , 从而
, 从而 的特征值等于1或-1.
的特征值等于1或-1.
证明 由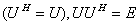
得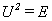
又因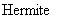 矩阵的特征值为实数, 所以根据定理1.2.8得,
矩阵的特征值为实数, 所以根据定理1.2.8得, 的特征值等于-1或1.
的特征值等于-1或1.
引理2.1设是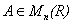 , 则
, 则 为正交矩阵的充要条件是存在酉矩阵
为正交矩阵的充要条件是存在酉矩阵 , 使
, 使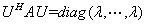 , 其中
, 其中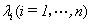 的模为1.
的模为1.
引理1.2.2[9] 设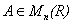 ,则
,则 为正交矩阵的充要条件是
为正交矩阵的充要条件是 有
有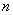 个两两正交的单位特征向量
个两两正交的单位特征向量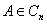 , 且特征值的模为1.
, 且特征值的模为1.
定理1.2.12 任一个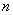 阶酉矩阵
阶酉矩阵 一定正交相似于分块对角矩阵
一定正交相似于分块对角矩阵
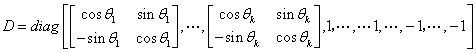
其中
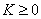 ,
,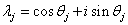 ,
, 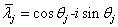 ,
,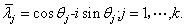
是 的所有不同的复特征值.
的所有不同的复特征值.
证明  的所有特征值全为
的所有特征值全为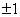 , 由引理1.2.1和引理1.2.2知
, 由引理1.2.1和引理1.2.2知 一定正交相似于对角矩阵
一定正交相似于对角矩阵
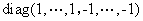
若 有复特征值
有复特征值
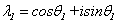
则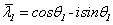
也是 的特征值. 因此可设有
的特征值. 因此可设有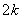 复特征值.
复特征值.
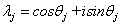 ,
, 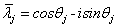 ,
,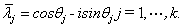
设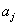 是属于
是属于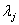 的单位特征向量, 则
的单位特征向量, 则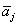 属于
属于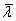 的单位特征向量. 根据酉矩阵属于不同特征值的向量两两正交. 于是
的单位特征向量. 根据酉矩阵属于不同特征值的向量两两正交. 于是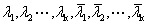 互不相同,
互不相同, 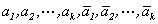 两两正交, 令
两两正交, 令
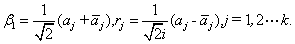
易知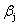 与
与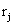 为相互正交的实向量. 设
为相互正交的实向量. 设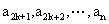 为
为 的属于特征值
的属于特征值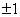 的相互正交的单位实特征向量, 则
的相互正交的单位实特征向量, 则
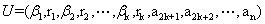
为一个酉矩阵.
因为
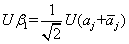
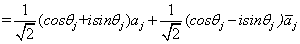
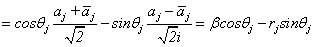
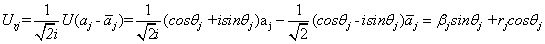
所以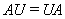 , 即
, 即 正交相似于
正交相似于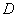 .
.
定理表明, 如果酉矩阵的特征根都是虚根, 则它在负数域上一定可对角化.
1.2.4. 酉矩阵的其它性质
定理1.2.13设 为上(下) 三角的酉矩阵, 则
为上(下) 三角的酉矩阵, 则 必为对角矩阵, 且主对角线上元素的模等于1.
必为对角矩阵, 且主对角线上元素的模等于1.
证明 不妨设 为上三角的酉矩阵, 则其逆
为上三角的酉矩阵, 则其逆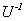 (上三角)等于其共轭转置
(上三角)等于其共轭转置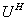 (下三角),所以
(下三角),所以 只能是对角矩阵, 又
只能是对角矩阵, 又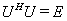 , 故可得
, 故可得 的主对角线上元素的模等于1.
的主对角线上元素的模等于1.
定理1.2.14 设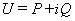 是酉矩阵, 其中
是酉矩阵, 其中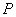 ,
,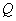 为实矩阵, 则
为实矩阵, 则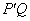 为实对称矩阵, 且
为实对称矩阵, 且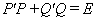 .
.
证明 由
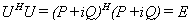
可得
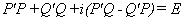
从而
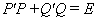 及
及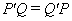
即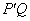 为实对称矩阵.
为实对称矩阵.
酉矩阵与正交矩阵均有许多良好的性质, 它们在线性代数理论、优化理论、计算方法等方面都占有重要的地位.
最近,研究了两个偶数阶正交矩阵之和是正交矩阵的充要条件问题, 并指出当 ,
,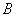 是奇数阶正交矩阵时,
是奇数阶正交矩阵时, 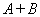 不可能是正交矩阵. 然而, 对酉矩阵来说, 结果有所不同.
不可能是正交矩阵. 然而, 对酉矩阵来说, 结果有所不同.
下面我们将证明, 对给定的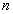 阶酉阵
阶酉阵 , 一定存在
, 一定存在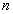 阶酉阵
阶酉阵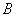 , 使
, 使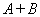 是酉阵, 并给出酉阵
是酉阵, 并给出酉阵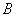 的表达式.
的表达式.
用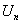 表示全体
表示全体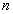 阶酉阵;
阶酉阵; 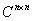 表示全体
表示全体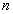 阶复矩阵.
阶复矩阵.
引理1.2.1复方阵 酉相似于对角阵的充要条件是
酉相似于对角阵的充要条件是 为复正规阵.
为复正规阵.
证明 必要性显然. 充分性由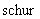 分解定理知, 任意复方阵
分解定理知, 任意复方阵 必可酉相似于上三角阵, 即存在
必可酉相似于上三角阵, 即存在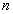 阶酉阵
阶酉阵 , 使
, 使
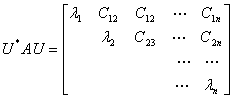 (1-2-1)
(1-2-1)
由条件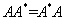 得
得
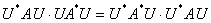 (1-2-2)
(1-2-2)
把(1-2-1)及其共轭转置式代入等式(1-2-2)直接计算可得
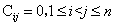
从而 酉相似于对角阵. 由于酉阵是复正规阵, 因此根据引理1知, 任一酉阵均酉相似于对角阵, 且对角线上元素的模长都为1.
酉相似于对角阵. 由于酉阵是复正规阵, 因此根据引理1知, 任一酉阵均酉相似于对角阵, 且对角线上元素的模长都为1.
定理1.2.15已知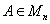 有特征值
有特征值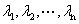 那么存在一个酉矩阵
那么存在一个酉矩阵 , 使得
, 使得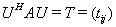
其中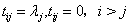 ,
,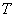 是上三角矩阵. 如果
是上三角矩阵. 如果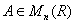 且
且 的所有特征值都是实数, 那么, 可选择
的所有特征值都是实数, 那么, 可选择 为实正交矩阵.
为实正交矩阵.
证明用归纳法证明.
设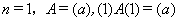 定理成立. 假设
定理成立. 假设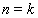 定理也成立, 当
定理也成立, 当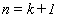 时.
时. 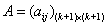 成立. 设
成立. 设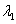 为
为 的特征值,
的特征值, 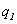 为它的单位特征向量, 由施密特正交化过程, 存在
为它的单位特征向量, 由施密特正交化过程, 存在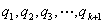 使
使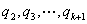 两两正交且构成
两两正交且构成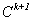 的标准正交基. 令
的标准正交基. 令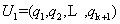 这是一个
这是一个 阵使
阵使
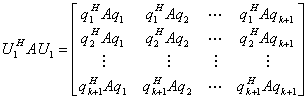
由于
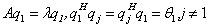
所以
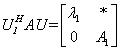
由于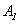 为
为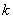 阶矩阵, 由归纳假设, 存在
阶矩阵, 由归纳假设, 存在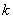 阶
阶 矩阵
矩阵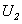 , 使
, 使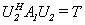 , 为上三角矩阵,令
, 为上三角矩阵,令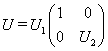 显然,
显然,  为由阵
为由阵
且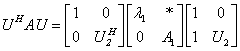
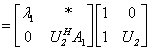
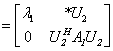
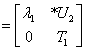
是上三角阵, 由归纳原理可知定理成立, 对于实阵与是正交阵的证明均可用数学归纳法证明.
第三节 酉矩阵的构造
1.3.1 二阶酉矩阵的构造
由定理1.1.2可知二阶矩阵 为酉矩阵的充分必要条件是
为酉矩阵的充分必要条件是 为下列三种形式之一 :
为下列三种形式之一 :
(i)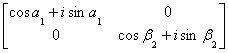
(ii)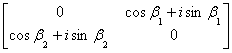
(iii)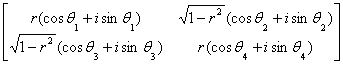
这里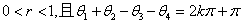 ,
, 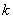 为整数.
为整数.
通过上式可以构造二阶的酉矩阵.
1.3.2通过运算性质构造酉矩阵
由酉矩阵的运算性质知:
(1) 若 为酉矩阵, 则
为酉矩阵, 则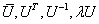 (其中
(其中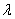 的为单位根)都是酉矩阵.
的为单位根)都是酉矩阵.
(2) 酉矩阵, 则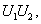
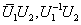 等也都是酉矩阵.
等也都是酉矩阵.
(3) 酉矩阵, 且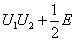 是反
是反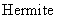 矩阵, 则
矩阵, 则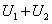 也是酉矩阵.
也是酉矩阵.
通过这些运算性质可以构造出新的酉矩阵.
1.3.3 利用施密特正交化构造酉矩阵
矩阵的正规性是检验矩阵是否可对角化的一个简单方法,任意正规矩阵都可在经过一个酉变换后变为对角矩阵,反过来,所有可在经过一个酉变换后变为对角矩阵都是正规矩阵.
在高等代数中,我们知道实对称矩阵一定正交相似于对角矩阵,并且讨论过,对已知实对称矩阵 , 求正交矩阵
, 求正交矩阵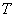 使得
使得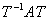 为对角矩阵的一般歩骤,类似的我们可以讨论,当
为对角矩阵的一般歩骤,类似的我们可以讨论,当 是正规矩阵时,求酉矩阵
是正规矩阵时,求酉矩阵 ,使得
,使得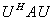 为对角矩阵,具体步骤如下:
为对角矩阵,具体步骤如下:
(1) 根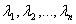 ;
;
(2) 求每一个相异特征值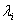 的特征向量
的特征向量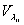 ;
;
(3) chur正交单位化的方法,求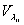 的标准正交基
的标准正交基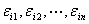 ;
;
(4) 命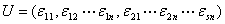 则酉矩阵
则酉矩阵 满足
满足
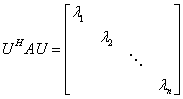
若 是正规矩阵,则
是正规矩阵,则 能酉相似于对角矩阵,即存在酉矩阵
能酉相似于对角矩阵,即存在酉矩阵 使得
使得
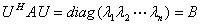
则
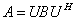
于是
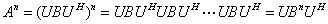
而对角矩阵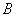 的
的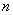 次幂是由各对角元素的
次幂是由各对角元素的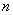 次幂组成,所以通过
次幂组成,所以通过 的相似对角矩阵求
的相似对角矩阵求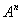 .
.
第二章 Hermite矩阵
为了论述方便,我们给出以下几个定义:
1.定义 矩阵A=[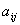 ]∈Mn(C)称为Hermite矩阵,是指A=A*,其中A*=
]∈Mn(C)称为Hermite矩阵,是指A=A*,其中A*=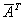 =[
=[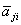 ]。如果A=-A*,则称之为斜Hermite矩阵。
]。如果A=-A*,则称之为斜Hermite矩阵。
2.定义 设A是n阶Hermite矩阵,如果任意x∈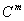 ,且x≠0,都有x*Ax>0,则称A为正定矩阵,记作A>0;如果任意x∈
,且x≠0,都有x*Ax>0,则称A为正定矩阵,记作A>0;如果任意x∈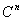 ,都有x*Ax≥0,则称A为非负定(半正定)矩阵,记作A≥0.
,都有x*Ax≥0,则称A为非负定(半正定)矩阵,记作A≥0.
3.定义 设A,B都是n阶Hermite矩阵,如果A—B≥O,则称A大于或等于B(或称B小于或等于A),记作A≥B(B≤A);如果A—B>0则称A大于B(或B小于A),记作A>B(B<A)。
第一节 关于Hermite矩阵的性质定理
(1)对所有A∈Mn,A+A*,AA*和A*A都是Hermite矩阵.
(2)如果A是Hermite矩阵,则对正整数k,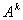 也是Hermite矩阵.
也是Hermite矩阵.
(3)如果A是可逆Hermite矩阵,则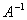 也是Hermite矩阵.
也是Hermite矩阵.
(4)如果A,B是Hermite矩阵,则对实数k,p,kA+pB也是Hermite矩阵
(5)对所有A∈Mn,A—A*是斜Hermite矩阵.(A—A*)=A*-A=-(A—A*)
(6)如果A,B是斜Hermite矩阵,那么对所有实数a,b,aA+bB是斜Hermite矩阵.
(7)如果A是Hermite矩阵,那么iA是斜Hermite矩阵,反之,A是斜Hermite矩阵,则iA是Hermite矩阵.
(8)任意A∈Mn可写成A=1/2(A+A*)+ 1/2(A—A*)=H(A)+S(A),其中H(A)=1/2(A+A*)是A的Hermite部分,而S(A)=1/2(A—A*)是A的斜Hermite部分。(由(1)和(5)知)
(9)如果A是Hermite矩阵,那么A的主对角元素是实数,为了给定A的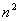 个元素,我们可以自由地给定任意n个实数(对于主对角元)和任意1/2(n一1)n个复数(对于非对角元)。(由定义可知
个元素,我们可以自由地给定任意n个实数(对于主对角元)和任意1/2(n一1)n个复数(对于非对角元)。(由定义可知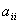 的共轭等于
的共轭等于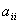 故
故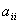 (i=1,2,3,…,n)为实数)。
(i=1,2,3,…,n)为实数)。
1.2定理 每个A∈Mn可以唯一地写成A=S+iT,其中S和T都是H矩阵,它也是唯一写成A=B+C,其中B是H矩阵,而C是斜H矩阵.
证明:把A写成A=1/2(A+A*)+i[-i/2(A—A*)],并且S=1/2(A+A*)和T=-i/2(A—A*)都是H矩阵。关于唯一性论断,如果A=E+iF,其中E和F都是H矩阵,那么2S=A+A*=(E+iF)+(E+iF)*=E+iF—E—iF=2E。
因而E=S,类似证明F=T,关于表示式A=B+C的论断同样方式可证。
注:这个定理充分说明了Hermite矩阵在矩阵中的地位相当于实数在复数中的地位。
第二节 Hermite矩阵的判定定理
2.1定理 设A=[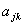 ]∈Mm×n(C),则A是Hermite矩阵的充分必要条件是对任意x∈
]∈Mm×n(C),则A是Hermite矩阵的充分必要条件是对任意x∈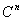 ,x*Ax是实数。
,x*Ax是实数。
证明:必要性,如果A是Hermite矩阵,则对任意x∈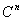 ,因为x*Ax是实数,所以x*Ax=(x*Ax)=x*A*x=x*Ax,因此x*Ax是实数;充分性,y∈
,因为x*Ax是实数,所以x*Ax=(x*Ax)=x*A*x=x*Ax,因此x*Ax是实数;充分性,y∈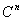 ,x*Ax,y*Ay,(x+y)*
,x*Ax,y*Ay,(x+y)*
A(x+y)都是实数,而(x+y)*A(x+y)=x*A(x+y)+y*A(x+y)=x*Ax+x*Ay+y*Ax+y*Ay于是对任意x,y∈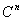 ,x*Ay+y*Ax是实数,特别地,令x=(0,0,…,1,0,…,0)
,x*Ay+y*Ax是实数,特别地,令x=(0,0,…,1,0,…,0)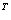 ,y=(0,0,…,1,0,…,0)
,y=(0,0,…,1,0,…,0)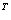 ,且x与y中的1分别是第j个和第k个分量,则x*Ay+y*Ax=
,且x与y中的1分别是第j个和第k个分量,则x*Ay+y*Ax=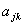 +
+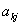 ,是实数,这表明
,是实数,这表明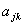 与
与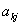 的虚部值相等,但符号相反,令x=(0,0,…,1,0,…,0)
的虚部值相等,但符号相反,令x=(0,0,…,1,0,…,0)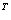 ,y=(0,0,…,1,0,…,0)
,y=(0,0,…,1,0,…,0)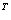 ,x中的第j个分量。y中的1是第k个分量.其中i
,x中的第j个分量。y中的1是第k个分量.其中i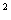 =-1,x*Ay+y*Ax=-
=-1,x*Ay+y*Ax=-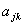 +
+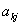 ,则
,则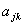 与
与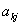 实部相等,因此
实部相等,因此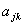 =
=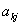 ,j,k=1,2,…,n.即A是Hermite矩阵。
,j,k=1,2,…,n.即A是Hermite矩阵。
2.2定理设A=[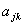 ]∈Mn是给定的,那么A是Hermite矩阵的充分必要条件是A是正规矩阵,且A的所有特征值都是实数。
]∈Mn是给定的,那么A是Hermite矩阵的充分必要条件是A是正规矩阵,且A的所有特征值都是实数。
证明:必要性,A是n阶Hermite矩阵,则A必酉相似于实对角矩阵,即存在n阶酉矩阵U使得U*AU=V,其中V=diag(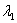 ,
,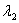 ,…,
,…,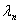 ),
),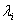 (i=1,2,…,n)是A的实特征值,且A*A=
(i=1,2,…,n)是A的实特征值,且A*A=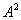 =AA*,即A是正规矩阵。
=AA*,即A是正规矩阵。
充分性,A是正规矩阵,则它可酉对角化,所以A=UVU*,其中V=diag(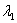 ,
,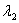 ,…,
,…,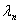 )是由A的各特征值构成的对角矩阵,一般有A*=UVU*,而V是实矩阵,故A=A*,即A是Hermite矩阵。
)是由A的各特征值构成的对角矩阵,一般有A*=UVU*,而V是实矩阵,故A=A*,即A是Hermite矩阵。
2.3定理 设A=[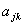 ]∈Mn,那么A是Hermite矩阵的充分必要条件是对所有S∈Mn,S*AS是Hermite矩阵。
]∈Mn,那么A是Hermite矩阵的充分必要条件是对所有S∈Mn,S*AS是Hermite矩阵。
证明:略.
2.4定理 (Hermite矩阵的谱定理)设A∈Mn,则A是Hermite矩阵的充分必要条件是存在酉矩阵U,使得U*AU=V= diag(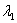 ,
,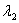 ,…,
,…,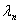 ),其中
),其中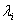 (i=1,2,…,n)均为实
(i=1,2,…,n)均为实
数。
证明:类似于定理2.2.
注:虽然Hermite矩阵实线性组合是Hermite矩阵,但它们复线性组合就不一定是Hermite矩阵,例如,若A是Hermite矩阵,那么只有当A=0时,iA才是Hemite矩阵,另外如果A和B是Hermite矩阵,那么(AB)*=B*A*=BA,因此AB是Hermite矩阵等价于A与B可交换。
第三节 Hermite矩阵的正定性
与实对称矩阵一样, 同样我们可以利用Hermite 二次型的正定(非负定) , 可以定义Hermite 矩阵的正定(非负定)。
3 . 1 正定(非负定)矩阵具有如下基本性质:
设A ,B 为Hermite 矩阵,
(1)单位矩阵 I> 0;
(2)若A > 0, 数k, 则 kA > 0;
(3)若A > 0,B> 0, 则A + B> 0;
(4)若A≥0,B≥0, 则A + B≥0 。
显然这些基本性质可以由定义直接推导
出。
3 . 2 Herm ite 矩阵A 正定(非负定)的条件。
定理3 . 2 . 1 设A 是 n 阶 Hermite 矩阵, 则
下列命题等价:
(1)A 是正定矩阵;
( 2)对任意 n 阶可逆矩阵 P*A P 都是Hermite 正定矩阵;
(3) A 的 n 个特征值均为正数;
(4)存在 n 阶可逆矩阵P,使得P3A P= 1;
(5)存在 n 阶可逆矩阵Q , 使得A = Q *Q;
(6)存在 n 阶可逆Hermite 矩阵S, 使得A =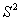 。
。
证明 (1)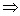 (2) 对任意 n 阶可逆矩阵 P及任意 y∈
(2) 对任意 n 阶可逆矩阵 P及任意 y∈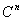 且y≠0, 令 x= Py, 则 x∈
且y≠0, 令 x= Py, 则 x∈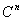 且 x≠0, y*(P*A P) y= x*A x> 0 。 故P*A P 是Herm ite 矩阵。
且 x≠0, y*(P*A P) y= x*A x> 0 。 故P*A P 是Herm ite 矩阵。
(2)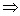 (3) 对 Hermite 矩阵A。由定理2 . 4 知存在酉矩阵U , 使U*AU = diag(
(3) 对 Hermite 矩阵A。由定理2 . 4 知存在酉矩阵U , 使U*AU = diag(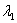 ,
,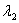 ,…,
,…,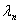 ), 其中
), 其中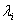 ( i= 1, 2, …, n) 为A的特征值, 由(2)知diag(
( i= 1, 2, …, n) 为A的特征值, 由(2)知diag(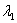 ,
,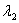 ,…,
,…,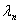 )是正定矩阵, 则其中
)是正定矩阵, 则其中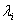 ( i= 1, 2, …, n)均为正数。
( i= 1, 2, …, n)均为正数。
(3)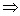 (4) 因为A 特征值
(4) 因为A 特征值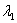 ,
,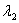 ,…,
,…,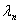 均为正数, 令
均为正数, 令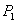 = diag ((1/
= diag ((1/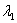 ),(1/
),(1/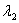 ),…,(1/
),…,(1/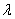 ))
))
P= U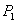 , 则 P 是可逆矩阵, 并且由 4 . 3 .1 有, P*AP= (U
, 则 P 是可逆矩阵, 并且由 4 . 3 .1 有, P*AP= (U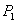 )*A (U
)*A (U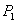 )=
)= 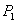 U*AU
U*AU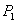 = I .
= I .
(4)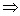 (5) 因为存在 n 阶可逆矩阵 P,使得 P*A P = I, 则令Q=
(5) 因为存在 n 阶可逆矩阵 P,使得 P*A P = I, 则令Q=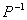 , 有 A =Q*Q;
, 有 A =Q*Q;
(5)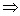 (1) 因为存在 n 阶可逆矩阵Q ,使得Q = Q*Q , 则对任意 x∈
(1) 因为存在 n 阶可逆矩阵Q ,使得Q = Q*Q , 则对任意 x∈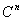 且x≠0都有Q x≠0, 从而 x*A x=(Q x)*(Q x) > 0; 故A 是正定矩阵。
且x≠0都有Q x≠0, 从而 x*A x=(Q x)*(Q x) > 0; 故A 是正定矩阵。
下面证明 (1)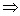 (6)设
(6)设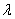 为A 的特征值, x 为相应的特征值向量, 则A x=
为A 的特征值, x 为相应的特征值向量, 则A x=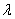 x,因为A 是正定矩阵, 所以
x,因为A 是正定矩阵, 所以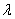 x*x= x*Ax> 0 从而
x*x= x*Ax> 0 从而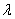 > 0, 因此A 的特征值均为正数, 又A = U diag(
> 0, 因此A 的特征值均为正数, 又A = U diag(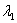 ,
,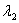 ,…,
,…,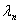 )U*, 其中
)U*, 其中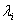 ( i= 1, 2, …, n)为A 的特征值, 令S=U diag ((1/
( i= 1, 2, …, n)为A 的特征值, 令S=U diag ((1/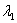 ),(1/
),(1/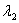 ),…,(1/
),…,(1/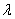 ))U*, 则 S 是 n 阶可逆Hermite 矩阵, 并且A =
))U*, 则 S 是 n 阶可逆Hermite 矩阵, 并且A =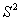 。
。
(6)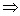 (1)因为存在阶可逆 Hermite 矩阵 S, 使得A =
(1)因为存在阶可逆 Hermite 矩阵 S, 使得A =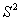 = S*S, 类似于(5)
= S*S, 类似于(5)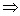 (1) , 即知A 是正定矩阵。
(1) , 即知A 是正定矩阵。
类似定理3 . 2 . 1, 有如下结论:
定理3 . 2 . 2 设A 是 n 阶 Hermite 正定矩阵, 下列命题等价
(1)A 是非负定实矩阵;
(2)对任意 n 阶可逆矩阵P,P*A P是Hermite 非负定矩阵;
(3)A的n个特征值均为非负数;
(4)存在 n 阶可逆矩阵 P 使得 P*A P=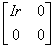 为其中 r= rank (A ) ;
为其中 r= rank (A ) ;
(5)存在秩为 r 的矩阵Q , 使得A = Q*Q;
(6)存在n 阶Herm ite 矩阵S, 使得A =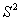 .
.
定理3 . 2 . 3 n 阶 Hermite矩阵A正定的充分必要条件是A 的顺序主子式均为正
数。
证明: 略
注: Hermite 矩阵A 的顺序主子式均非负, 并不能推出A 是非负定矩阵。例如A =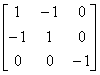 是 Hermite 矩阵, 即是如此。
是 Hermite 矩阵, 即是如此。
定理3 . 2 . 4 n 阶H 矩阵A 正定的充分必要条件是A 的所有主子式全大于零。
证明: 略
例 3 . 2 . 1 若A , C 均为 n 阶 Hermite矩阵且AC=CA , 则AC为正定矩阵。
证:因为(AC)*= C*A*= CA = AC, 所以AC 是Hermite矩阵, 又因为A > 0, 由定理3 . 2 . 1 知, 存在n 阶可逆Hermite矩阵B 使A=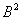 于是
于是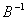 (AC)B= BCB= B*CB 则A与
(AC)B= BCB= B*CB 则A与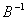 CB 具有相同的特征值, 由 C> 0 及定理 3 . 2 . 1 知B*CB> 0, 从而AC 的特征值均为正数, 由3 . 2 . 1 知AC> 0 .
CB 具有相同的特征值, 由 C> 0 及定理 3 . 2 . 1 知B*CB> 0, 从而AC 的特征值均为正数, 由3 . 2 . 1 知AC> 0 .
第四节 矩阵不等式
利用Hermite矩阵的非负性可以在Hermite矩阵类中引进偏序, 从而可以讨论矩阵不等式当矩阵的阶数为 1 时, 此偏序与实数是一致的, 故矩阵不等式是数值不等式的推广, 并且矩阵不等式在现代控制论等科学中具有重要的应用。由定义3 知, 对n阶Hermite矩阵A与B, 如果A≥B, 则对任意 x∈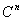 , 都有 x*A x≥x*Bx, 反之亦然。注意: (1)任意两个实可以比较大小, 但任意两个n阶 Hermite矩阵未必能比较大小,即并非A≥B 或B≤A 两者之中必有一个成立. 例如, 对
, 都有 x*A x≥x*Bx, 反之亦然。注意: (1)任意两个实可以比较大小, 但任意两个n阶 Hermite矩阵未必能比较大小,即并非A≥B 或B≤A 两者之中必有一个成立. 例如, 对
A=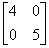 B=
B=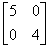
A≥B 和B≤A 均不成立.
(2)对任意两个实数a 和b 如果a 不大于b,则有a= b, 但对两个n (n≥2)阶 Hermite 矩
阵A 和B. 从A≥B 和A≯B, 不能推出A =B,例如对A=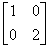 ,B=
,B=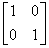 可见
可见
A≥B 和A≯B, 但A≠B.
4 . 1 下面讨论矩阵不等式的一些性质。
定理4 . 1 . 1 设A ,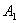 ,B,
,B,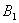 , C 均为 Hermite
, C 均为 Hermite
矩阵, 则
(1)若A≥B,B≥C 则A≥C (传递性)
(2)若A ≥B (A > B) , k> 0, 则 kA ≥kB
(kA > kB). (线性性)
(3)若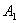 ≥
≥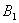 ,
,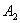 ≥
≥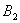 , 则
, 则
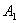 +
+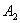 ≥
≥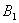 +
+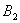 .
.
(4)若A ,B 皆为n 阶Hermite 矩阵且A
≥B, P 为n×m 矩阵, 则
P*A P≥P*BP;
(5)若A≥B (A > B)的充分必要条件是
若-A≤-B(-A<-B)
(6)若A≥0, -A≥0 则A = 0;
(7)若A≥0,B≥0 则A + B≥0
(8)若A≥0,B> 0 则A + B> 0
(9)若A≥B,B> C 则A > C
( 10)若A > 0, (A≥0) , C> 0, (C≥0)且AC= CA , 则AC> 0, (AC≥0)
证明: (1)至(5)显然成立.
(6) 若 A , 则 A 的特征值均非负, 而-A的特征值恰为A的特征值的相反数, 则- A 可知,A 的特征值又必须全部非正, 因此H 矩阵A 的特征值全部为零, 由定理3 . 2 . 4 知A = 0 .
(7)和(8)由正定(非负定)矩阵的基本性质即得, 而(9)是(8)的直接推论.
(10)由例 3 . 2 . 1 可得.
定理4 . 1 . 2 设A 是 n 阶 Hermite 矩阵, 则
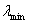 (A ) I≤A≤
(A ) I≤A≤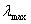 (A ) I, 这时
(A ) I, 这时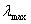 (A )和
(A )和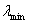 (A )分别表示A 的最大和最小值.
(A )分别表示A 的最大和最小值.
证明: 由定理 3 . 4 知, 存在酉矩阵U 使得A= U diag(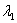 ,
,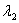 ,…,
,…,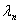 )U*
)U*
其中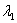 ≥
≥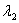 ≥…≥
≥…≥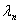 是矩阵A 特征值, 则
是矩阵A 特征值, 则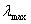 (A ) =
(A ) = 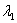 ,
,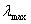 (A )-
(A )-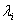 ≥0,
≥0, 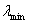 (A )
(A )
=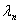 ,
, 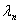 -
-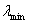 (A )≥0 ( i= 1, 2, …n)并且
(A )≥0 ( i= 1, 2, …n)并且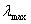 (A ) I- A = U [
(A ) I- A = U [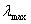 (A ) I-diag(
(A ) I-diag(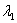 ,
,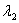 ,…,
,…,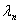 )U *≥0
)U *≥0
A -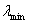 (A ) I= U [ diag (
(A ) I= U [ diag (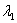 ,
,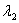 ,…,
,…,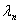 )-
)-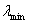 (A ) I]U *≥0
(A ) I]U *≥0
即K m in (A ) I≤A≤K max (A ) I .
总结
本文探讨酉矩阵的性质与构造。首先在酉矩阵与正交矩阵的关系开始入手, 在酉矩阵的代数性质方面加以探究。在已有酉矩阵的定义的基础上, 讨论:酉矩阵的逆、酉矩阵的转置、酉矩阵的方幂、酉矩阵的数乘、酉矩阵的乘法、酉矩阵的伴随矩阵是否仍为酉矩阵, 对酉矩阵的运算性质进行总结和概括。对运用运算性质构造酉矩阵做好铺垫。
本文主要从Hermite矩阵的性质,判定定理,正定性和矩阵不等式等几个方面探讨Hermite 矩阵的重要性, 从而使读者对复数矩阵中的Hermite矩阵有一个全面深刻的理解其中设计的证明和性质与实对称矩阵十分相似, 进一步让学生认识到Hermite矩阵在Mn(C)中的地位相当于实数在复数C中的地位。
总的来说, 通过对本文的研究受益匪浅. 但也存在不足:一方面写作水平有限, 在文中不乏表达欠妥当之处;另一方面, 见识学浅, 对某些问题认识不够深刻, 或存在偏见, 还请多多指教。
参考文献
[1] 原永久, 郭元春, 牛凤文. 高等代数[M]. 吉林: 吉林大学出版社, 2000:177-182.
[2] 任富田. 关于正交矩阵之和是正交矩阵的充要条件[J]. 数学通报,1999:1-4.
[3] 杨明. 矩阵论[M ]. 武汉:华东科技大学出版社.2006:23-77
[4] F. zhang . Matrix theory basic resultes and techniques. Springer, New York,Berlin,
[5] 丘维声.高等代数[M]. 北京:高等教育出版社,1996:114-211.
[6] 北京大学数学系几何与代数教研室前代数小组. 正交矩阵的若干性质[J], 2003:3-11
[7] 戴华. 矩阵论[M ] . 北京: 科学出版社, 20## .
[8 陈景良, 陈向晖. 特殊矩阵[M ] . 北京: 清华大学出版社, 20## .
[9 R. A. 合恩, C. R. 约翰逊; 杨奇(译) , 侯自新(审校) ; 矩阵分析[M ] . 天津: 天津大学出版社,1989 .
[10]昌. 矩阵分析[M ] . 北京: 北京理工大学出版社, 1996 .
-
特殊矩阵总结
特殊矩阵总结常用的产生通用特殊矩阵的函数有zeros产生全0矩阵零矩阵ones产生全1矩阵幺矩阵eye产生单位矩阵rand产生01…
-
我的矩阵分析总结
矩阵分析期末复习1判断一个集合是否为线性空间只需要验证2条加法封闭性乘法封闭性例1Sx1x2x3x1x2x301234142Sxx…
-
矩阵论小结
矩阵论线性空间定义本质是个集合满足一定条件下的集合首先定义了加法运算满足加法的交换结合律在这个集合中能找到零元素与负元素然后定义数…
-
矩阵理论考试总结
1向量矩阵是一个严密的数学概念数组是计算机上的一个名词一组数而已非要赋予数组数学含义则一维数组相当于向量二维数组相当于矩阵矩阵是数…
-
矩阵解题总结
矩阵解题总结迄今我们都做了不少的矩阵习题我们常常以刷题来满足自己的做题欲望并以此方法来让自己对矩阵这个新概念有更好的了解那么在我们…
-
科研训练总结 研究矩阵理论
科研训练总结数学科学学院柏慧荣2910102024本学期我参加了学院组织的科研训练讨论课,我参与的方向主要是研究矩阵理论。虽然上课…
-
管理学基础理论总结
第一章管理概述管理从事计划组织控制领导和激励五项基本活动管理的工作有效性是从效率和效力效果来看的即高效做事做正确的事用正确的方法管…
-
矩阵论小结
矩阵论线性空间定义本质是个集合满足一定条件下的集合首先定义了加法运算满足加法的交换结合律在这个集合中能找到零元素与负元素然后定义数…
-
矩阵理论考试总结
1向量矩阵是一个严密的数学概念数组是计算机上的一个名词一组数而已非要赋予数组数学含义则一维数组相当于向量二维数组相当于矩阵矩阵是数…
-
总结求矩阵的逆矩阵的方法
总结求矩阵的逆矩阵的方法课程名称专业班级成员组成联系方式摘要矩阵是线性代数的主要内容很多实际问题用矩阵的思想去解既简单又快捷逆矩阵…
-
矩阵式管理优缺点总结
目前,受国际管理新理念的影响,一种交叉、双向的管理模式已经在越来越多的公司开始运用,它就是矩阵式管理,采用这种管理模式的企业,在构…