等比数列题型归纳总结
课题:等比数列
教学目标:掌握等比数列的定义,通项公式和前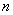 项和的公式,掌握等比数列的有关性质,并能利用这些知识解决有关问题,培养学生的化归能力.
项和的公式,掌握等比数列的有关性质,并能利用这些知识解决有关问题,培养学生的化归能力.
教学重点:等比数列的判断,通项公式和前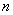 项和的公式以及等比数列的有关性质的应用.
项和的公式以及等比数列的有关性质的应用.
(一) 主要知识:

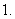 等比数列的概念及其通项公式,等比数列前
等比数列的概念及其通项公式,等比数列前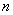 项和公式;
项和公式;
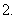 等比数列的有关性质;
等比数列的有关性质;
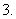 等比数列的充要条件:
等比数列的充要条件:

 是等比数列
是等比数列 (
(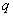 为非零常数);
为非零常数);

 是等比数列
是等比数列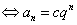 (
(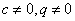 )
)
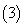
 是等比数列
是等比数列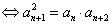
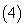
 是等比数列
是等比数列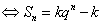 (
(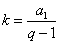 ,
,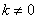 ,
,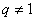 )
)
(二)主要方法:
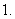 涉及等比数列的基本概念的问题,常用基本量
涉及等比数列的基本概念的问题,常用基本量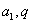 来处理;
来处理;
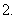 已知三个数成等比数列时,可设这三个数依次为
已知三个数成等比数列时,可设这三个数依次为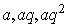 或
或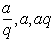 ;四个数时设为
;四个数时设为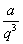 、
、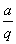 、
、 、
、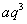
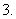 等比数列的相关性质:
等比数列的相关性质:
 若
若 是等比数列,则
是等比数列,则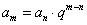 ;
;
 若
若 是等比数列,
是等比数列,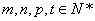 ,当
,当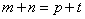 时,
时,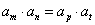
特别地,当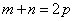 时,
时,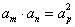
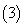 若
若 是等比数列,则下标成等差数列的子列构成等比数列;
是等比数列,则下标成等差数列的子列构成等比数列;
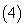 若
若 是等比数列,
是等比数列,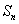 是
是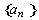 的前
的前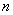 项和,则
项和,则 ,
,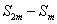 ,
, 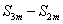 …成等比数列.
…成等比数列.
 两个等比数列
两个等比数列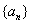 与
与 的积、商、倒数的数列
的积、商、倒数的数列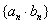 、
、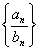 、
、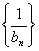 仍为等比数列.
仍为等比数列.
【典型例题】
题型一:基本量运算
例1、已知 为等比数列,
为等比数列, ,
,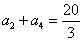 ,求
,求 的通项公式;
的通项公式;
例2、在等比数列 中,
中, ,
,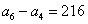 ,
, ,求公比
,求公比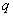 、
、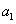 及
及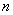
问题2. 已知数列
已知数列 是等比数列,且
是等比数列,且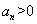 ,
,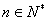 ,
, ,
,
则
 (
( 苏州调研)在等比数列
苏州调研)在等比数列 中,
中, ,
, ,
, ,则
,则



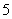
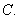

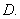
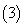 (
( 湖北文)在等比数列
湖北文)在等比数列 中,
中,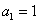 ,
,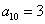 ,则
,则




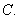

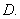
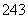
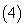 (
( 全国Ⅱ文)在
全国Ⅱ文)在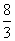 和
和 之间插入三个数,使五个数成等比数列,则插入的三个数的乘积是
之间插入三个数,使五个数成等比数列,则插入的三个数的乘积是
 (
( 南京高三期末调研)在等比数列
南京高三期末调研)在等比数列 中,已知
中,已知 ,
,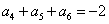 ,
,
则该数列前 项的和
项的和
问题3.( 全国Ⅱ)数列
全国Ⅱ)数列 的前
的前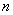 项和记为
项和记为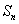 ,已知
,已知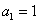 ,
, (
(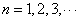 ) 证明:
) 证明: 数列
数列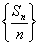 是等比数列,
是等比数列,

问题4.已知数列 中,
中,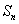 是它的前
是它的前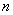 项和,且
项和,且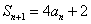
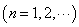 ,
,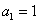 .
.
 设
设
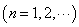 ,求证:数列
,求证:数列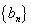 是等比数列;
是等比数列; 设
设
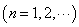 ,
,
求证: 是等差数列;
是等差数列;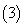 求
求 的通项公式
的通项公式 及前
及前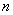 项和公式
项和公式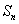
问题5.( 陕西)已知正项数列
陕西)已知正项数列 ,其前
,其前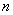 项和
项和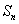 满足
满足 且
且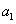 ,
,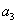 ,
, 成等比数列,求数列
成等比数列,求数列 的通项
的通项
(四)巩固练习:
 (
( 湖南文)在等比数列
湖南文)在等比数列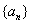 (
(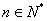 )中,若
)中,若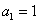 ,
,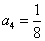 ,则该数列的前
,则该数列的前 项和为
项和为 



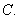

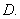

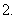 (
( 海南文)已知
海南文)已知 、
、 、
、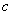 、
、 成等比数列,且曲线
成等比数列,且曲线 的顶点是
的顶点是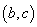 ,
,
则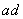 等于
等于 
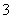

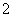
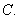

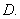
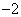
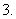 (
( 重庆)设
重庆)设 为公比
为公比 的等比数列,若
的等比数列,若 和
和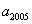 是方程
是方程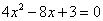 的两根,则
的两根,则 ______.
______.
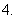 (
( 湖北)若数列
湖北)若数列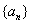 满足
满足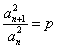 (
(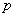 为正常数,
为正常数, ),则称
),则称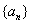 为“等方比数列”.甲:数列
为“等方比数列”.甲:数列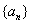 是等方比数列; 乙:数列
是等方比数列; 乙:数列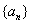 是等比数列,则
是等比数列,则
 甲是乙的充分条件但不是必要条件
甲是乙的充分条件但不是必要条件 甲是乙的必要条件但不是充分条件
甲是乙的必要条件但不是充分条件
 甲是乙的充要条件
甲是乙的充要条件  甲既不是乙的充分条件也不是乙的必要条件
甲既不是乙的充分条件也不是乙的必要条件
(五)走向高考:
 (
( 陕西)各项均为正数的等比数列
陕西)各项均为正数的等比数列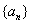 的前
的前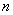 项和为
项和为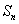 为,若
为,若 ,
, ,
,
则 等于
等于 



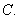
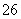
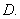

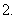 (
( 辽宁)在等比数列
辽宁)在等比数列 中,
中, ,前
,前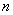 项和为
项和为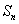 ,若数列
,若数列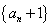 也是等比数列,则
也是等比数列,则
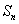 等于
等于 



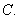

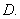
 (
( 湖北)设等比数列
湖北)设等比数列 的公比为
的公比为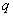 ,前
,前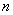 项和为
项和为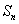 ,若
,若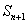 ,
,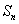 ,
, 成等差数列,则
成等差数列,则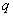 的值为
的值为
 (
( 全国文Ⅱ)设等比数列
全国文Ⅱ)设等比数列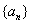 的公比
的公比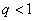 ,前
,前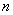 项和为
项和为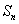 .已知
.已知 ,
,
求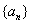 的通项公式.
的通项公式.
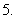 (
( 北京)数列
北京)数列 中,
中,
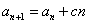 (
(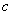 是常数,
是常数,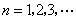 ),且
),且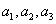
成公比不为 的等比数列.(Ⅰ)求
的等比数列.(Ⅰ)求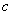 的值;(Ⅱ)求
的值;(Ⅱ)求 的通项公式.
的通项公式.
 (
( 山东)设数列
山东)设数列 满足
满足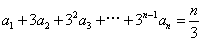 ,
, .
.
(Ⅰ)求数列 的通项;(Ⅱ)设
的通项;(Ⅱ)设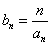 ,求数列
,求数列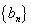 的前
的前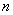 项和
项和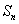 .
.
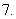 (
( 福建文)已知数列
福建文)已知数列 满足
满足
(Ⅰ)证明:数列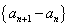 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若数列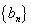 满足
满足 证明
证明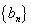 是等差数列。
是等差数列。
第二篇:例说等比数列题型
例说等比数列题型
【例1】 已知Sn是数列{an}的前n项和,Sn=pn(p∈R,n∈N*),那么数列{an}.
[ ]
A.是等比数列
B.当p≠0时是等比数列
C.当p≠0,p≠1时是等比数列
D.不是等比数列
分析 由Sn=pn(n∈N*),有a1=S1=p,并且当n≥2时,
an=Sn-Sn-1=pn-pn-1=(p-1)pn-1

但满足此条件的实数p是不存在的,故本题应选D.
说明 数列{an}成等比数列的必要条件是an≠0(n∈N*),还要注

【例2】 已知等比数列1,x1,x2,…,x2n,2,求x1·x2·x3·…·x2n.
解 ∵1,x1,x2,…,x2n,2成等比数列,公比q
∴2=1·q2n+1
x1x2x3…x2n=q·q2·q3…q2n=q1+2+3+…+2n

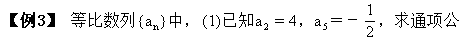
式;(2)已知a3·a4·a5=8,求a2a3a4a5a6的值.
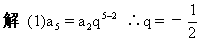
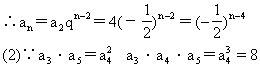
∴a4=2

【例4】 已知a>0,b>0且a≠b,在a,b之间插入n个正数x1,x2,…,xn,使得a,x1,x2,…,xn,b成等比数列,求
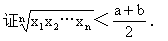
证明 设这n+2个数所成数列的公比为q,则b=aqn+1
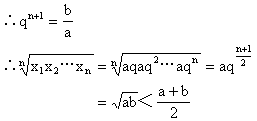
【例5】 设a、b、c、d成等比数列,求证:(b-c)2+(c-a)2+(d-b)2=(a-d)2.
证法一 ∵a、b、c、d成等比数列
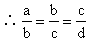
∴b2=ac,c2=bd,ad=bc
∴左边=b2-2bc+c2+c2-2ac+a2+d2-2bd+b2
=2(b2-ac)+2(c2-bd)+(a2-2bc+d2)
=a2-2ad+d2
=(a-d)2=右边
证毕.
证法二 ∵a、b、c、d成等比数列,设其公比为q,则:
b=aq,c=aq2,d=aq3
∴左边=(aq-aq2)2+(aq2-a)2+(aq3-aq)2
=a2-2a2q3+a2q6
=(a-aq3)2
=(a-d)2=右边
证毕.
说明 这是一个等比数列与代数式的恒等变形相综合的题目.证法一是抓住了求证式中右边没有b、c的特点,走的是利用等比的条件消去左边式中的b、c的路子.证法二则是把a、b、c、d统一化成等比数列的基本元素a、q去解决的.证法二稍微麻烦些,但它所用的统一成基本元素的方法,却较证法一的方法具有普遍性.
【例6】 求数列的通项公式:
(1){an}中,a1=2,an+1=3an+2
(2){an}中,a1=2,a2=5,且an+2-3an+1+2an=0
思路:转化为等比数列.
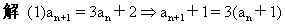
∴{an+1}是等比数列
∴an+1=3·3n-1 ∴an=3n-1
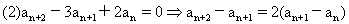
∴{an+1-an}是等比数列,即
an+1-an=(a2-a1)·2n-1=3·2n-1
再注意到a2-a1=3,a3-a2=3·21,a4-a3=3·22,…,an-an-1=3·2n-2,这些等式相加,即可以得到

说明 解题的关键是发现一个等比数列,即化生疏为已知.(1)中发现{an+1}是等比数列,(2)中发现{an+1-an}是等比数列,这也是通常说的化归思想的一种体现.

证 ∵a1、a2、a3、a4均为不为零的实数

∴上述方程的判别式Δ≥0,即
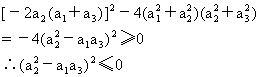
又∵a1、a2、a3为实数
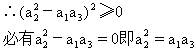
因而a1、a2、a3成等比数列

∴a4即为等比数列a1、a2、a3的公比.
【例8】 若a、b、c成等差数列,且a+1、b、c与a、b、c+2都成等比数列,求b的值.
解 设a、b、c分别为b-d、b、b+d,由已知b-d+1、b、b+d与b-d、b、b+d+2都成等比数列,有

整理,得

∴b+d=2b-2d 即b=3d
代入①,得
9d2=(3d-d+1)(3d+d)
9d2=(2d+1)·4d
解之,得d=4或d=0(舍)
∴b=12
【例9】 已知等差数列{an}的公差和等比数列{bn}的公比都是d,又知d≠1,且a4=b4,a10=b10:
(1)求a1与d的值;
(2)b16是不是{an}中的项?
思路:运用通项公式列方程
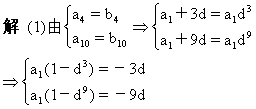

(2)∵b16=b1·d15=-32b1

∴b16=-32b1=-32a1,如果b16是{an}中的第k项,则
-32a1=a1+(k-1)d
∴(k-1)d=-33a1=33d
∴k=34即b16是{an}中的第34项.
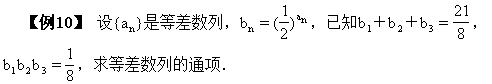
解 设等差数列{an}的公差为d,则an=a1+(n-1)d


解这个方程组,得
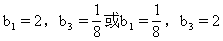
∴a1=-1,d=2或a1=3,d=-2
∴当a1=-1,d=2时,an=a1+(n-1)d=2n-3
当a1=3,d=2时,an=a1+(n-1)d=5-2n
【例11】 三个数成等比数列,若第二个数加4就成等差数列,再把这个等差数列的第3项加32又成等比数列,求这三个数.
解法一 按等比数列设三个数,设原数列为a,aq,aq2
由已知:a,aq+4,aq2成等差数列
即:2(aq+4)=a+aq2 ①
a,aq+4,aq2+32成等比数列
即:(aq+4)2=a(aq2+32)


解法二 按等差数列设三个数,设原数列为b-d,b-4,b+d
由已知:三个数成等比数列
即:(b-4)2=(b-d)(b+d)

b-d,b,b+d+32成等比数列
即b2=(b-d)(b+d+32)


解法三 任意设三个未知数,设原数列为a1,a2,a3
由已知:a1,a2,a3成等比数列

a1,a2+4,a3成等差数列
得:2(a2+4)=a1+a3 ②
a1,a2+4,a3+32成等比数列
得:(a2+4)2=a1(a3+32) ③

说明 将三个成等差数列的数设为a-d,a,a+d;将三个成

简化计算过程的作用.
【例12】 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
分析 本题有三种设未知数的方法
方法一 设前三个数为a-d,a,a+d,则第四个数由已知条

方法二 设后三个数为b,bq,bq2,则第一个数由已知条件推得为2b-bq.
方法三 设第一个数与第二个数分别为x,y,则第三、第四个数依次为12-y,16-x.
由这三种设法可利用余下的条件列方程组解出相关的未知数,从而解出所求的四个数,



所求四个数为:0,4,8,16或15,9,3,1.
解法二 设后三个数为:b,bq,bq2,则第一个数为:2b-bq


所求四个数为:0,4,8,16或15,9,3,1.
解法三 设四个数依次为x,y,12-y,16-x.
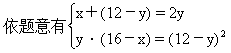

这四个数为0,4,8,16或15,9,3,1.
【例13】 已知三个数成等差数列,其和为126;另外三个数成等比数列,把两个数列的对应项依次相加,分别得到85,76,84.求这两个数列.
解 设成等差数列的三个数为b-d,b,b+d,由已知,b-d+b+b+d=126
∴b=42
这三个数可写成42-d,42,42+d.
再设另三个数为a,aq,aq2.由题设,得

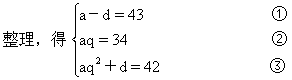
解这个方程组,得
a1=17或a2=68
当a=17时,q=2,d=-26
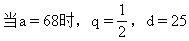
从而得到:成等比数列的三个数为17,34,68,此时成等差的三个数为68,42,16;或者成等比的三个数为68,34,17,此时成等差的三个数为17,42,67.
【例14】 已知在数列{an}中,a1、a2、a3成等差数列,a2、a3、a4成等比数列,a3、a4、a5的倒数成等差数列,证明:a1、a3、a5成等比数列.
证明 由已知,有
2a2=a1+a3 ①



即 a3(a3+a5)=a5(a1+a3)

所以a1、a3、a5成等比数列.
【例15】 已知(b-c)logmx+(c-a)logmy+(a-b)logmz=0.
(1)设a,b,c依次成等差数列,且公差不为零,求证:x,y,z成等比数列.
(2)设正数x,y,z依次成等比数列,且公比不为1,求证:a,b,c成等差数列.
证明 (1)∵a,b,c成等差数列,且公差d≠0
∴b-c=a-b=-d,c-a=2d
代入已知条件,得:-d(logmx-2logmy+logmz)=0
∴logmx+logmz=2logmy
∴y2=xz
∵x,y,z均为正数
∴x,y,z成等比数列
(2)∵x,y,z成等比数列且公比q≠1
∴y=xq,z=xq2代入已知条件得:
(b-c)logmx+(c-a)logmxq+(a-b)logmxq2=0
变形、整理得:(c+a-2b)logmq=0
∵q≠1 ∴logmq≠0
∴c+a-2b=0 即2b=a+c
即a,b,c成等差数列
-
等比数列题型总结
等比数列常见题型总结作者:fansx021(原创)题型一1、等比数列{an}中,已知a2?3,a9?384,则an?2、在等比数列…
-
等比数列题型归纳总结
课题等比数列教学目标掌握等比数列的定义通项公式和前n项和的公式掌握等比数列的有关性质并能利用这些知识解决有关问题培养学生的化归能力…
-
等比数列知识点总结及题型归纳(5.17)
等比数列知识点总结及题型归纳1等比数列的定义2通项公式ana1qn1a1nqABna1q0AB0首项a1公比qqanqnamanq…
-
高中数学复习系列---数列常见题型总结
高中数学复习系列---数列(常见、常考题型总结)题型一:求值类的计算题(多关于等差等比数列)A)根据基本量求解(方程的思想)1、已…
-
等比数列知识点总结及题型归纳
等比数列知识点总结及题型归纳1等比数列的定义2通项公式anqq0n2且nNq称为公比an1ana1qn1a1nqABna1q0AB…
-
等差数列题型总结、知识点
等差数列一.等差数列知识点:1:①如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常…
-
高中数学等差数列题型总结
一、等差数列1、数列的概念例1.根据数列前4项,写出它的通项公式:(1)1,3,5,7??;(2)2?122,3?132,4?14…
-
等差数列知识点题型总结
等差数列一、知识回顾题型一:等差数列的基本运算1、等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则2.已知…
-
新课程高中数学数列题型总结
高中数学数列复习题型总结1.等差等比数列(n?1)??S12.Sn与an的关系:an??,已知Sn求an,应分n?1时a1?n?2…
-
数列常见题型总结
高中数学《数列》常见、常考题型总结题型一:求值类的计算题(多关于等差等比数列)A)根据基本量求解(方程的思想)1、已知Sn为等差数…
-
等比数列题型总结
等比数列常见题型总结作者:fansx021(原创)题型一1、等比数列{an}中,已知a2?3,a9?384,则an?2、在等比数列…