椭圆的几何性质知识点归纳及典型例题及练习(付答案)
(一)椭圆的定义:
1、椭圆的定义:平面内与两个定点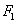 、
、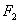 的距离之和等于定长(大于
的距离之和等于定长(大于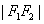 )的点的轨迹叫做椭圆。这两个定点
)的点的轨迹叫做椭圆。这两个定点 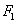 、
、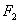 叫做椭圆的焦点,两焦点的距离
叫做椭圆的焦点,两焦点的距离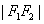 叫做椭圆的焦距。
叫做椭圆的焦距。
对椭圆定义的几点说明:
(1)“在平面内”是前提,否则得不到平面图形(去掉这个条件,我们将得到一个椭球面);
(2)“两个定点”的设定不同于圆的定义中的“一个定点”,学习时注意区分;
(3)作为到这两个定点的距离的和的“常数”,必须满足大于| F1F2|这个条件。若不然,当这个“常数”等于| F1F2|时,我们得到的是线段F1F2;当这个“常数”小于| F1F2|时,无轨迹。这两种特殊情况,同学们必须注意。
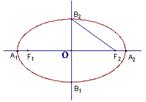
(4)下面我们对椭圆进行进一步观察,发现它本身具备对称性,有两条对称轴和一个对称中心,我们把它的两条对称轴与椭圆的交点记为A1, A2, B1, B2,于是我们易得| A1A2|的值就是那个“常数”,且|B2F2|+|B2F1|、|B1F2|+|B1F1|也等于那个“常数”。同学们想一想其中的道理。


(5)中心在原点、焦点分别在x轴上,y 轴上的椭圆标准方程分别为:

相同点是:形状相同、大小相同;都有 a > b > 0 ,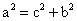 。
。
不同点是:两种椭圆相对于坐标系的位置不同,它们的焦点坐标也不同(第一个椭圆的焦点坐标为(-c,0)和(c,0),第二个椭圆的焦点坐标为(0,-c)和(0,c)。椭圆的焦点在 x 轴上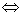 标准方程中x2项的分母较大;椭圆的焦点在 y 轴上
标准方程中x2项的分母较大;椭圆的焦点在 y 轴上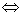 标准方程中y2项的分母较大。
标准方程中y2项的分母较大。
(二)椭圆的几何性质:
椭圆的几何性质可分为两类:一类是与坐标系有关的性质,如顶点、焦点、中心坐标;一类是与坐标系无关的本身固有性质,如长、短轴长、焦距、离心率.对于第一类性质,只要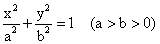 的有关性质中横坐标x和纵坐标y互换,就可以得出
的有关性质中横坐标x和纵坐标y互换,就可以得出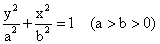 的有关性质。总结如下:
的有关性质。总结如下:

几点说明:
(1)长轴:线段 ,长为
,长为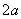 ;短轴:线段
;短轴:线段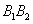 ,长为
,长为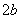 ;焦点在长轴上。
;焦点在长轴上。
(2)对于离心率e,因为a>c>0,所以0<e<1,离心率反映了椭圆的扁平程度。
由于 ,所以
,所以 越趋近于1,
越趋近于1,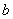 越趋近于
越趋近于 ,椭圆越扁平;
,椭圆越扁平; 越趋近于0,
越趋近于0,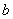 越趋近于
越趋近于 ,椭圆越圆。
,椭圆越圆。
(3)观察下图, ,所以
,所以 ,所以椭圆的离心率e = cos∠OF2B2
,所以椭圆的离心率e = cos∠OF2B2
(三)直线与椭圆:
直线 :
: (
( 、
、 不同时为0)
不同时为0)
椭圆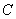 :
: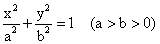
那么如何来判断直线和椭圆的位置关系呢?将两方程联立得方程组,通过方程组的解的个数来判断直线和椭圆交点的情况。方法如下:
 消去
消去 得到关于
得到关于 的一元二次方程,化简后形式如下
的一元二次方程,化简后形式如下
 ,
, 
(1)当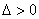 时,方程组有两组解,故直线与椭圆有两个交点;
时,方程组有两组解,故直线与椭圆有两个交点;
(2)当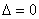 时,方程组有一解,直线与椭圆有一个公共点(相切);
时,方程组有一解,直线与椭圆有一个公共点(相切);
(3)当 时,方程组无解,直线和椭圆没有公共点。
时,方程组无解,直线和椭圆没有公共点。
注:当直线与椭圆有两个公共点时,设其坐标为 ,那么线段
,那么线段 的长度(即弦长)为
的长度(即弦长)为 ,设直线的斜率为
,设直线的斜率为 ,
,
可得:
 ,然后我们可通过求出方程的根或用韦达定理求出。
,然后我们可通过求出方程的根或用韦达定理求出。
典型例题一
例1 椭圆的一个顶点为 ,其长轴长是短轴长的2倍,求椭圆的标准方程.
,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置.
解:(1)当 为长轴端点时,
为长轴端点时, ,
,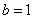 ,
,
椭圆的标准方程为: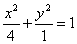 ;
;
(2)当 为短轴端点时,
为短轴端点时, ,
, ,
,
椭圆的标准方程为: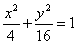 ;
;
说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.
典型例题二
例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.
解: ∴
∴ ,
,
∴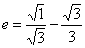 .
.
说明:求椭圆的离心率问题,通常有两种处理方法,一是求 ,求
,求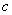 ,再求比.二是列含
,再求比.二是列含 和
和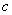 的齐次方程,再化含
的齐次方程,再化含 的方程,解方程即可.
的方程,解方程即可.
典型例题三
例3 已知中心在原点,焦点在 轴上的椭圆与直线
轴上的椭圆与直线 交于
交于 、
、 两点,
两点, 为
为 中点,
中点, 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.
的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.
解:由题意,设椭圆方程为 ,
,
由 ,得
,得 ,
,
∴ ,
,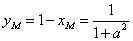 ,
,
 ,∴
,∴ ,
,
∴ 为所求.
为所求.
说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.
典型例题四
例4椭圆 上不同三点
上不同三点 ,
, ,
, 与焦点
与焦点 的距离成等差数列.
的距离成等差数列.
(1)求证 ;
;
(2)若线段 的垂直平分线与
的垂直平分线与 轴的交点为
轴的交点为 ,求直线
,求直线 的斜率
的斜率 .
.
证明:(1)由椭圆方程知 ,
, ,
, .
.
由圆锥曲线的统一定义知: ,
,
∴ 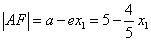 .
.
同理  .
.
∵ 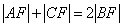 ,且
,且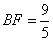 ,
,
∴ 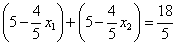 ,
,
即  .
.
(2)因为线段 的中点为
的中点为 ,所以它的垂直平分线方程为
,所以它的垂直平分线方程为
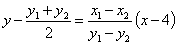 .
.
又∵点 在
在 轴上,设其坐标为
轴上,设其坐标为 ,代入上式,得
,代入上式,得

又∵点 ,
,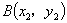 都在椭圆上,
都在椭圆上,
∴ 
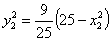
∴ 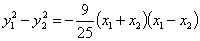 .
.
将此式代入①,并利用 的结论得
的结论得
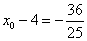
∴  .
.
典型例题五
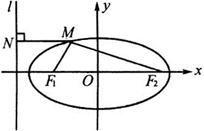 例5 已知椭圆
例5 已知椭圆 ,
,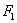 、
、 为两焦点,问能否在椭圆上找一点
为两焦点,问能否在椭圆上找一点 ,使
,使 到左准线
到左准线 的距离
的距离 是
是 与
与 的等比中项?若存在,则求出点
的等比中项?若存在,则求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解:假设 存在,设
存在,设 ,由已知条件得
,由已知条件得
 ,
, ,∴
,∴ ,
, .
.
∵左准线 的方程是
的方程是 ,
,
∴ .
.
又由焦半径公式知:
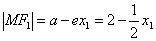 ,
,
 .
.
∵ ,
,
∴ .
.
整理得 .
.
解之得 或
或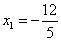 . ①
. ①
另一方面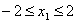 . ②
. ②
则①与②矛盾,所以满足条件的点 不存在.
不存在.
说明:
(1)利用焦半径公式解常可简化解题过程.
(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.
(3)本例也可设 存在,推出矛盾结论(读者自己完成).
存在,推出矛盾结论(读者自己完成).
典型例题六
例6 已知椭圆 ,求过点
,求过点 且被
且被 平分的弦所在的直线方程.
平分的弦所在的直线方程.
分析一:已知一点求直线,关键是求斜率,故设斜率为 ,利用条件求
,利用条件求 .
.
解法一:设所求直线的斜率为 ,则直线方程为
,则直线方程为 .代入椭圆方程,并整理得
.代入椭圆方程,并整理得
 .
.
由韦达定理得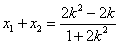 .
.
∵ 是弦中点,∴
是弦中点,∴ .故得
.故得 .
.
所以所求直线方程为 .
.
分析二:设弦两端坐标为 、
、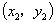 ,列关于
,列关于 、
、 、
、 、
、 的方程组,从而求斜率:
的方程组,从而求斜率: .
.
解法二:设过 的直线与椭圆交于
的直线与椭圆交于 、
、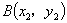 ,则由题意得
,则由题意得

①-②得 . ⑤
. ⑤
将③、④代入⑤得 ,即直线的斜率为
,即直线的斜率为 .
.
所求直线方程为 .
.
说明:
(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.
(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.
(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.
典型例题七
例7 求适合条件的椭圆的标准方程.
(1)长轴长是短轴长的2倍,且过点 ;
;
(2)在 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.
轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.
分析:当方程有两种形式时,应分别求解,如(1)题中由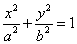 求出
求出 ,
, ,在得方程
,在得方程 后,不能依此写出另一方程
后,不能依此写出另一方程 .
.
解:(1)设椭圆的标准方程为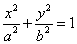 或
或 .
.
由已知 . ①
. ①
又过点 ,因此有
,因此有
 或
或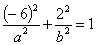 . ②
. ②
由①、②,得 ,
, 或
或 ,
, .故所求的方程为
.故所求的方程为
 或
或 .
.
(2)设方程为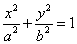 .由已知,
.由已知, ,
, ,所以
,所以 .故所求方程为
.故所求方程为 .
.
说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程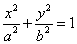 或
或 .
.
典型例题八
例8 椭圆 的右焦点为
的右焦点为 ,过点
,过点 ,点
,点 在椭圆上,当
在椭圆上,当 为最小值时,求点
为最小值时,求点 的坐标.
的坐标.
分析:本题的关键是求出离心率 ,把
,把 转化为
转化为 到右准线的距离,从而得最小值.一般地,求
到右准线的距离,从而得最小值.一般地,求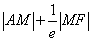 均可用此法.
均可用此法.
 解:由已知:
解:由已知: ,
, .所以
.所以 ,右准线
,右准线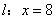 .
.
过 作
作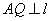 ,垂足为
,垂足为 ,交椭圆于
,交椭圆于 ,故
,故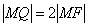 .显然
.显然 的最小值为
的最小值为 ,即
,即 为所求点,因此
为所求点,因此 ,且
,且 在椭圆上.故
在椭圆上.故 .所以
.所以 .
.
说明:本题关键在于未知式 中的“2”的处理.事实上,如图,
中的“2”的处理.事实上,如图, ,即
,即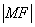 是
是 到右准线的距离的一半,即图中的
到右准线的距离的一半,即图中的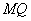 ,问题转化为求椭圆上一点
,问题转化为求椭圆上一点 ,使
,使 到
到 的距离与到右准线距离之和取最小值.
的距离与到右准线距离之和取最小值.
典型例题九
例9 求椭圆 上的点到直线
上的点到直线 的距离的最小值.
的距离的最小值.
分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.
解:椭圆的参数方程为 设椭圆上的点的坐标为
设椭圆上的点的坐标为 ,则点到直线的距离为
,则点到直线的距离为
 .
.
当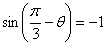 时,
时, .
.
说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.
典型例题十
例10 设椭圆的中心是坐标原点,长轴在 轴上,离心率
轴上,离心率 ,已知点
,已知点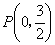 到这个椭圆上的点的最远距离是
到这个椭圆上的点的最远距离是 ,求这个椭圆的方程,并求椭圆上的点
,求这个椭圆的方程,并求椭圆上的点 的距离等于
的距离等于 的点的坐标.
的点的坐标.
分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求 的最大值时,要注意讨论
的最大值时,要注意讨论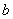 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.
的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.
解法一:设所求椭圆的直角坐标方程是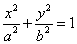 ,其中
,其中 待定.
待定.
由 可得
可得
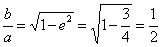 ,即
,即 .
.
设椭圆上的点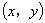 到点
到点 的距离是
的距离是 ,则
,则
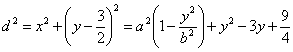

其中 .
.
如果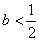 ,则当
,则当 时,
时, (从而
(从而 )有最大值.
)有最大值.
由题设得 ,由此得
,由此得 ,与
,与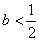 矛盾.
矛盾.
因此必有 成立,于是当
成立,于是当 时,
时, (从而
(从而 )有最大值.
)有最大值.
由题设得 ,可得
,可得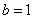 ,
, .
.
∴所求椭圆方程是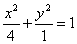 .
.
由 及求得的椭圆方程可得,椭圆上的点
及求得的椭圆方程可得,椭圆上的点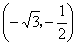 ,点
,点 到点
到点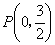 的距离是
的距离是 .
.
解法二:根据题设条件,可取椭圆的参数方程是 ,其中
,其中 ,待定,
,待定, ,
,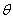 为参数.
为参数.
由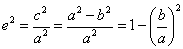 可得
可得
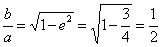 ,即
,即 .
.
设椭圆上的点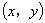 到点
到点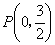 的距离为
的距离为 ,则
,则

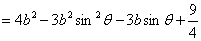

如果 ,即
,即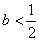 ,则当
,则当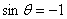 时,
时, (从而
(从而 )有最大值.
)有最大值.
由题设得 ,由此得
,由此得 ,与
,与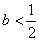 矛盾,因此必有
矛盾,因此必有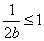 成立.
成立.
于是当 时
时 (从而
(从而 )有最大值.
)有最大值.
由题设知 ,∴
,∴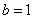 ,
, .
.
∴所求椭圆的参数方程是 .
.
由 ,
, ,可得椭圆上的是
,可得椭圆上的是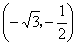 ,
, .
.
典型例题十一
例11 设 ,
, ,
,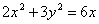 ,求
,求 的最大值和最小值.
的最大值和最小值.
分析:本题的关键是利用形数结合,观察方程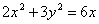 与椭圆方程的结构一致.设
与椭圆方程的结构一致.设 ,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.
,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.
解:由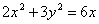 ,得
,得

可见它表示一个椭圆,其中心在 点,焦点在
点,焦点在 轴上,且过(0,0)点和(3,0)点.
轴上,且过(0,0)点和(3,0)点.
设 ,则
,则

它表示一个圆,其圆心为(-1,0)半径为 .
.
在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即 ,此时
,此时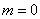 ;当圆过(3,0)点时,半径最大,即
;当圆过(3,0)点时,半径最大,即 ,∴
,∴ .
.
∴ 的最小值为0,最大值为15.
的最小值为0,最大值为15.

典型例题十二
例12 已知椭圆 ,
, 、
、 是其长轴的两个端点.
是其长轴的两个端点.
(1)过一个焦点 作垂直于长轴的弦
作垂直于长轴的弦 ,求证:不论
,求证:不论 、
、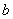 如何变化,
如何变化, .
.
(2)如果椭圆上存在一个点 ,使
,使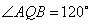 ,求
,求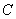 的离心率
的离心率 的取值范围.
的取值范围.
分析:本题从已知条件出发,两问都应从 和
和 的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率
的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率 满足的不等式,只能是椭圆的固有性质:
满足的不等式,只能是椭圆的固有性质: ,
,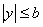 ,根据
,根据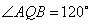 得到
得到 ,将
,将 代入,消去
代入,消去 ,用
,用 、
、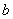 、
、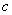 表示
表示 ,以便利用
,以便利用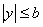 列出不等式.这里要求思路清楚,计算准确,一气呵成.
列出不等式.这里要求思路清楚,计算准确,一气呵成.
解:(1)设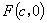 ,
,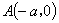 ,
,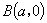 .
.

于是 ,
, .
.
∵ 是
是 到
到 的角.
的角.
∴
∵
∴
故 ∴
∴ .
.
(2)设 ,则
,则 ,
, .
.
由于对称性,不妨设 ,于是
,于是 是
是 到
到 的角.
的角.
∴
∵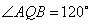 , ∴
, ∴
整理得
∵
∴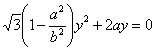
∵ , ∴
, ∴
∵ , ∴
, ∴
 ,
,
∴ ,
,
∴ 或
或 (舍),∴
(舍),∴ .
.
典型例题十三
例13 已知椭圆 的离心率
的离心率 ,求
,求 的值.
的值.
分析:分两种情况进行讨论.
解:当椭圆的焦点在 轴上时,
轴上时,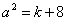 ,
, ,得
,得 .由
.由 ,得
,得 .
.
当椭圆的焦点在 轴上时,
轴上时, ,
,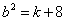 ,得
,得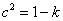 .
.
由 ,得
,得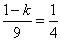 ,即
,即 .
.
∴满足条件的 或
或 .
.
说明:本题易出现漏解.排除错误的办法是:因为 与9的大小关系不定,所以椭圆的焦点可能在
与9的大小关系不定,所以椭圆的焦点可能在 轴上,也可能在
轴上,也可能在 轴上.故必须进行讨论.
轴上.故必须进行讨论.
典型例题十四
例14 已知椭圆 上一点
上一点 到右焦点
到右焦点 的距离为
的距离为
 ,求
,求 到左准线的距离.
到左准线的距离.
分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.
解法一:由 ,得
,得 ,
, ,
, .
.
由椭圆定义, ,得
,得
 .
.
由椭圆第二定义,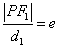 ,
,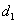 为
为 到左准线的距离,
到左准线的距离,
∴ ,
,
即 到左准线的距离为
到左准线的距离为 .
.
解法二:∵ ,
, 为
为 到右准线的距离,
到右准线的距离, ,
,
∴ .
.
又椭圆两准线的距离为 .
.
∴ 到左准线的距离为
到左准线的距离为 .
.
说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.
椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.
典型例题十五
例15 设椭圆 (
( 为参数)上一点
为参数)上一点 与
与 轴正向所成角
轴正向所成角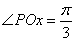 ,求
,求 点坐标.
点坐标.
分析:利用参数 与
与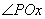 之间的关系求解.
之间的关系求解.
解:设 ,由
,由 与
与 轴正向所成角为
轴正向所成角为 ,
,
∴ ,即
,即 .
.
而 ,
, ,由此得到
,由此得到 ,
,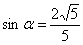 ,
,
∴ 点坐标为
点坐标为 .
.
 典型例题十六
典型例题十六
例16 设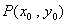 是离心率为
是离心率为 的椭圆
的椭圆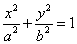
 上的一点,
上的一点, 到左焦点
到左焦点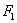 和右焦点
和右焦点 的距离分别为
的距离分别为 和
和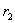 ,求证:
,求证: ,
, .
.
分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.
解: 点到椭圆的左准线
点到椭圆的左准线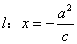 的距离,
的距离, ,
,
由椭圆第二定义,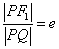 ,
,
∴ ,由椭圆第一定义,
,由椭圆第一定义, .
.
说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在 轴上的焦半径公式.
轴上的焦半径公式.
 典型例题十七
典型例题十七
例17 已知椭圆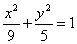 内有一点
内有一点 ,
,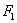 、
、 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点 是椭圆上一点.
是椭圆上一点.
(1) 求 的最大值、最小值及对应的点
的最大值、最小值及对应的点 坐标;
坐标;
(2) 求 的最小值及对应的点
的最小值及对应的点 的坐标.
的坐标.
分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.
解:(1)如上图, ,
, ,
,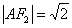 ,设
,设 是椭圆上任一点,由
是椭圆上任一点,由 ,
, ,∴
,∴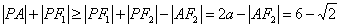 ,等号仅当
,等号仅当 时成立,此时
时成立,此时 、
、 、
、 共线.
共线.
由 ,∴
,∴ ,等号仅当
,等号仅当 时成立,此时
时成立,此时 、
、 、
、 共线.
共线.
建立 、
、 的直线方程
的直线方程 ,解方程组
,解方程组 得两交点
得两交点
 、
、 .
.
综上所述, 点与
点与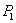 重合时,
重合时, 取最小值
取最小值 ,
, 点与
点与 重合时,
重合时, 取最大值
取最大值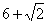 .
.
(2)如下图,设 是椭圆上任一点,作
是椭圆上任一点,作 垂直椭圆右准线,
垂直椭圆右准线, 为垂足,由
为垂足,由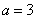 ,
, ,∴
,∴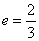 .由椭圆第二定义知
.由椭圆第二定义知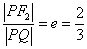 ,∴
,∴ ,∴
,∴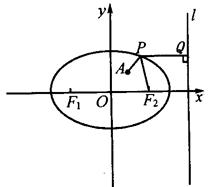
 ,要使其和最小需有
,要使其和最小需有 、
、 、
、 共线,即求
共线,即求 到右准线距离.右准线方程为
到右准线距离.右准线方程为 .
.
∴ 到右准线距离为
到右准线距离为 .此时
.此时 点纵坐标与
点纵坐标与 点纵坐标相同为1,代入椭圆得满足条件的点
点纵坐标相同为1,代入椭圆得满足条件的点 坐标
坐标 .
.
说明:求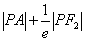 的最小值,就是用第二定义转化后,过
的最小值,就是用第二定义转化后,过 向相应准线作垂线段.巧用焦点半径
向相应准线作垂线段.巧用焦点半径 与点准距
与点准距 互化是解决有关问题的重要手段.
互化是解决有关问题的重要手段.
典型例题十八
例18 (1)写出椭圆 的参数方程;
的参数方程;
(2)求椭圆内接矩形的最大面积.
分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.
解:(1) 
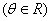 .
.
(2)设椭圆内接矩形面积为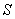 ,由对称性知,矩形的邻边分别平行于
,由对称性知,矩形的邻边分别平行于 轴和
轴和 轴,设
轴,设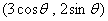 为矩形在第一象限的顶点,
为矩形在第一象限的顶点, ,
,
则
故椭圆内接矩形的最大面积为12.
说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.
典型例题十九
例19 已知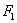 ,
, 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上一点,且
是椭圆上一点,且 .
.
(1)求椭圆离心率的取值范围;(2)求证 的面积与椭圆短轴长有关.
的面积与椭圆短轴长有关.
分析:不失一般性,可以设椭圆方程为
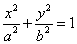 (
( ),
),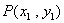 (
( ).
).
思路一:根据题设容易想到两条直线的夹角公式,即 ,设
,设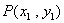 ,
, ,
, ,化简可得
,化简可得 .又
.又 ,两方程联立消去
,两方程联立消去 得
得 ,由
,由 ,可以确定离心率的取值范围;解出
,可以确定离心率的取值范围;解出 可以求出
可以求出 的面积,但这一过程很繁.
的面积,但这一过程很繁.
思路二:利用焦半径公式 ,
,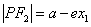 ,在
,在 中运用余弦定理,求
中运用余弦定理,求 ,再利用
,再利用 ,可以确定离心率
,可以确定离心率 的取值范围,将
的取值范围,将 代入椭圆方程中求
代入椭圆方程中求 ,便可求出
,便可求出 的面积.
的面积.
思路三:利用正弦定理、余弦定理,结合 求解.
求解.
解:(法1)设椭圆方程为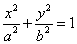 (
( ),
),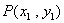 ,
, ,
, ,
, ,
,
则 ,
,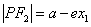 .
.
在 中,由余弦定理得
中,由余弦定理得
 ,
,
解得 .
.
(1)∵ ,
,
∴ ,即
,即 .
.
∴ .
.
故椭圆离心率的取范围是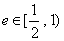 .
.
(2)将 代入
代入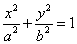 得
得
 ,即
,即 .
.
∴ .
.
即 的面积只与椭圆的短轴长有关.
的面积只与椭圆的短轴长有关.
(法2)设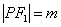 ,
, ,
, ,
,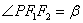 ,
,
则 .
.
(1)在 中,由正弦定理得
中,由正弦定理得
 .
.
∴
∵ ,
,
∴ ,
,
∴
 .
.
当且仅当 时等号成立.
时等号成立.
故椭圆离心率的取值范围是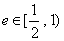 .
.
(2)在 中,由余弦定理得:
中,由余弦定理得:



∵ ,
,
∴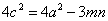 ,即
,即 .
.
∴ .
.
即 的面积与椭圆短轴长有关.
的面积与椭圆短轴长有关.
说明:椭圆上的一点 与两个焦点
与两个焦点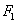 ,
, 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现
构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现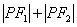 的结构,这样就可以应用椭圆的定义,从而可得到有关
的结构,这样就可以应用椭圆的定义,从而可得到有关 ,
, 的关系式,使问题找到解决思路.
的关系式,使问题找到解决思路.
典型例题二十
例20 椭圆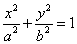
 与
与 轴正向交于点
轴正向交于点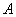 ,若这个椭圆上总存在点
,若这个椭圆上总存在点 ,使
,使 (
( 为坐标原点),求其离心率
为坐标原点),求其离心率 的取值范围.
的取值范围.
分析:∵ 、
、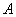 为定点,
为定点, 为动点,可以
为动点,可以 点坐标作为参数,把
点坐标作为参数,把 ,转化为
,转化为 点坐标的一个等量关系,再利用坐标的范围建立关于
点坐标的一个等量关系,再利用坐标的范围建立关于 、
、 、
、 的一个不等式,转化为关于
的一个不等式,转化为关于 的不等式.为减少参数,易考虑运用椭圆参数方程.
的不等式.为减少参数,易考虑运用椭圆参数方程.
解:设椭圆的参数方程是
 ,
,
则椭圆上的点 ,
, ,
,
∵ ,∴
,∴ ,
,
即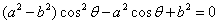 ,解得
,解得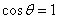 或
或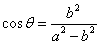 ,
,
∵ ∴
∴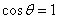 (舍去),
(舍去), ,又
,又
∴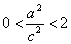 ,
,
∴ ,又
,又 ,∴
,∴ .
.
说明:若已知椭圆离心率范围 ,求证在椭圆上总存在点
,求证在椭圆上总存在点 使
使 .如何证明?
.如何证明?
[例1]求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点P到两焦点的距离的和等于10;
(2)两个焦点的坐标分别是(0,-2),(0,2),并且椭圆经过点(- ,
, );
);
(3)焦点在坐标轴上,且经过点A(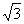 ,-2)和B(-2
,-2)和B(-2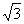 ,1)
,1)
分析:根据题意,先判断椭圆的焦点位置,后设椭圆的标准方程,求出椭圆中的a、b即可。若判断不出焦点在哪个轴上,可采用标准方程的统一形式。
解析:(1)因为椭圆的焦点在x轴上,所以设它的标准方程为 =1(a>b>0)
=1(a>b>0)
∵2a=10,2c=8,∴a=5,c=4
∴b2=a2-c2=52-42=9
所以所求的椭圆的标准方程为 =1
=1
(2)因为椭圆的焦点在y轴上,所以设它的标准方程为 =1(a>b>0)
=1(a>b>0)
由椭圆的定义知,
2a=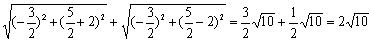
又c=2,∴b2=a2-c2=10-4=6
所以所求的椭圆的标准方程为 =1
=1
(3)解法一:若焦点在x轴上,设所求椭圆方程为 =1(a>b>0)
=1(a>b>0)
由A(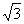 ,-2)和B(-2
,-2)和B(-2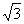 ,1)两点在椭圆上可得:
,1)两点在椭圆上可得:
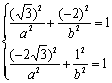 解之得
解之得
若焦点在y轴上,设所求椭圆方程为 =1(a>b>0),同上可解得
=1(a>b>0),同上可解得 ,不合题意,舍去。
,不合题意,舍去。
故所求的椭圆方程为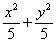 =1
=1
解法二:设所求椭圆方程为mx2+ny2=1(m>0,n>0且m≠n)。
由A(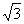 ,-2)和B(-2
,-2)和B(-2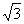 ,1)两点在椭圆上可得
,1)两点在椭圆上可得
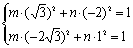
即 ,解得
,解得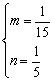
故所求的椭圆方程为 =1
=1
点评:(1)求椭圆的标准方程时,首先应明确椭圆的焦点位置,再用待定系数法求a、b。
(2)第(3)小题中的椭圆是存在且惟一的,为计算简便,可设其方程为mx2+ny2=1(m>0,n>0),不必考虑焦点位置,直接可求得方程.想一想,为什么?

[例2]已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。
分析:在解析几何里,求符合某种条件的点的轨迹方程,要建立适当的坐标系.为选择适当的坐标系,常常需要画出草图。如图所示,由△ABC的周长等于16,|BC|=6可知,点A到B、C两点的距离的和是常数,即|AB|+|AC|=16-6=10,因此,点A的轨迹是以B、C为焦点的椭圆,据此可建立坐标系并画出草图。
解析:如图所示,建立坐标系,使x轴经过点B、C,原点O与BC的中点重合。
由已知|AB|+|AC|+|BC|=16,|BC|=6,有|AB|+|AC|=10,即点A的轨迹是以B、C为焦点的椭圆,且2c=6,2a=10,
∴c=3,a=5,b2=52-32=16。
由于点A在直线BC上时,即y=0时,A、B、C三点不能构成三角形,所以点A的轨迹方程是 =1(y≠0)。
=1(y≠0)。
点评:椭圆的定义在解题中有着广泛的应用,另外,求出曲线的方程后,要检查一下方程的曲线上的点是否都符合题意,如果有不符合题意的点,应在方程后注明,常用限制条件来注明。
[例3]一动圆与已知圆O1:(x+3)2+y2=1外切,与圆O2:(x-3)2+y2=81内切,试求动圆圆心的轨迹方程。
分析:两圆相切时,圆心之间的距离与两圆的半径有关,可以找到动圆圆心满足的条件。
解析:两定圆的圆心和半径分别为O1(-3,0),r1=1;O2(3,0),r2=9
设动圆圆心为M(x,y),半径为R,则由题设条件可得|MO1|=1+R,|MO2|=9-R
∴|MO1|+|MO2|=10
由椭圆的定义知:M在以O1、O2为焦点的椭圆上,且a=5,c=3。
∴b2=a2-c2=25-9=16
故动圆圆心的轨迹方程为 =1。
=1。
点评:正确地利用两圆内切、外切的条件,合理地消去变量R,运用椭圆定义是解决本题的关键,这种求轨迹方程的方法叫做定义法。
 [例4]已知P是椭圆
[例4]已知P是椭圆 =1上的一点,F1、F2是两个焦点,且∠F1PF2=30°,求△PF1F2的面积。
=1上的一点,F1、F2是两个焦点,且∠F1PF2=30°,求△PF1F2的面积。
分析:如图所示,已知∠P=30°,要求△PF1F2的面积,如用 |F1F2|·|yP|,因为求P点坐标较繁,所以用S△=
|F1F2|·|yP|,因为求P点坐标较繁,所以用S△= |PF1|·|PF2|·sin30°较好,为此必须先求出|PF1|·|PF2|,从结构形式可看出用余弦定理可得出夹30°角的两边的乘积。
|PF1|·|PF2|·sin30°较好,为此必须先求出|PF1|·|PF2|,从结构形式可看出用余弦定理可得出夹30°角的两边的乘积。
解析:由方程 =1,得a=5,b=4,
=1,得a=5,b=4,
∴c=3,∴|F1F2|=2c=6
|PF1|+|PF2|=2a=10
∵∠F1PF2=30°
在△F1PF2中,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos30°
即62=|PF1|2+2|PF1|·|PF2|+|PF2|2-2|PF1|·|PF2|-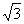 ·|PF1|·|PF2|
·|PF1|·|PF2|
(2+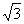 )|PF1|·|PF2|=(|PF1|+|PF2|)2-36=100-36=64,
)|PF1|·|PF2|=(|PF1|+|PF2|)2-36=100-36=64,
∴|PF1|·|PF2|= =64(2-
=64(2-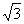 )
)
∴ =
= |PF1|·|PF2|·sin30°=
|PF1|·|PF2|·sin30°= ·64(2-
·64(2-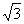 )·
)· =16(2-
=16(2-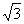 )
)
[例5]椭圆ax2+by2=1与直线x+y=1相交于P、Q两点,若|PQ|=2 ,且PQ的中点C与椭圆中心连线的斜率为
,且PQ的中点C与椭圆中心连线的斜率为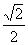 ,求椭圆方程。
,求椭圆方程。
分析:该题是求椭圆方程,即利用题设中的两个独立条件,求出a、b之值即可
解析:由 得(a+b)x2-2bx+b-1=0
得(a+b)x2-2bx+b-1=0
设P(x1,y1),Q(x2,y2),则
x1+x2= ,x1x2=
,x1x2=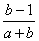
∴|PQ|=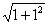
 ·
·
=
∴ =a+b ①
=a+b ①
又PQ的中点C( ,1-
,1- ),即C(
),即C( ,
,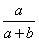 )
)
∴kOC=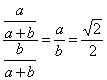 ② 由①②得a=
② 由①②得a=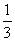 ,b=
,b=
∴所求椭圆方程为 =1
=1
[例6]中心在原点的椭圆C的一个焦点是F(0, ),又这个椭圆被直线l:y=3x-2截得的弦的中点的横坐标是
),又这个椭圆被直线l:y=3x-2截得的弦的中点的横坐标是 ,求该椭圆方程。
,求该椭圆方程。
分析:本题中涉及到弦的中点及弦所在直线的斜率,故可采用“平方差法”。
解析:据题意,此椭圆为焦点在y轴上的标准形式的椭圆,设其方程为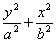 =1(a>b>0)
=1(a>b>0)
设直线l与椭圆C的交点分别为A(x1,y1),B(x2,y2),则有:
 =1,
=1,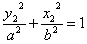
两式相减得: =0
=0
∴
即3= ∴a2=3b2 ①
∴a2=3b2 ①
 又因为椭圆焦点为F(0,
又因为椭圆焦点为F(0, ) ∴c=
) ∴c=
则a2-b2=50 ②
由①②解得:a2=75,b2=25
∴该椭圆方程为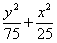 =1
=1
[例7]设P是椭圆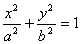 (a>b>0)上的一点,F1、F2是椭圆的焦点,且∠F1PF2=90°,求证:椭圆的离心率e≥
(a>b>0)上的一点,F1、F2是椭圆的焦点,且∠F1PF2=90°,求证:椭圆的离心率e≥
证明:∵P是椭圆上的点,F1、F2是焦点,由椭圆的定义,得|PF1|+|PF2|=2a ①
在Rt△F1PF2中, 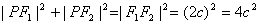
由①2,得
∴|PF1|·|PF2|=2(a2-c2) ②
由①和②,据韦达定理逆定理,知|PF1|·|PF2|是方程z2-3az+2(a2-c2)=0的两根,
则△=4a2-8(a2-c2)≥0,
∴(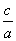 )2≥
)2≥ ,即e≥
,即e≥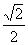
1. 如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是
A. (0,+∞) B. (0,2)
C. (1,+∞) D. (0,1)
2. 已知椭圆 =1,F1、F2分别为它的两焦点,过F1的焦点弦CD与x轴成α角(0<α<π=,则△F2CD的周长为
=1,F1、F2分别为它的两焦点,过F1的焦点弦CD与x轴成α角(0<α<π=,则△F2CD的周长为
A. 10 B. 12 C. 20 D. 不能确定
3. 椭圆 =1的一个焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是
=1的一个焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是
A. ± B. ±
B. ± C. ±
C. ± D. ±
D. ±
4. 设椭圆 =1的两焦点分别是F1和F2,P为椭圆上一点,并且PF1⊥PF2,则||PF1|-|PF2||等于
=1的两焦点分别是F1和F2,P为椭圆上一点,并且PF1⊥PF2,则||PF1|-|PF2||等于
A. 6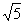 B. 2
B. 2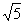 C.
C.  D.
D. 
5. 直线y=x与椭圆 +y2=1相交于A、B两点,则|AB|等于
+y2=1相交于A、B两点,则|AB|等于
A. 2 B.  C.
C.  D.
D. 
6. 点P是椭圆 =1上一点,F1、F2是其焦点,且∠F1PF2=60°,则△F1PF2的面积为___________。
=1上一点,F1、F2是其焦点,且∠F1PF2=60°,则△F1PF2的面积为___________。
7. △ABC的两顶点B(-8,0),C(8,0),AC边上的中线BM与AB边上的中线CN的长度之和为30,则顶点A的轨迹方程为___________。
8. F1、F2为定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则M点的轨迹是___________。
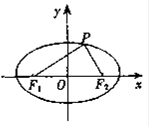
9. 以两坐标轴为对称轴的椭圆过点P( ,-4)和Q(-
,-4)和Q(-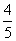 ,3),则此椭圆的方程是___________。
,3),则此椭圆的方程是___________。
10. 在椭圆 =1内,过点(2,1)且被这点平分的弦所在的直线方程是___________。
=1内,过点(2,1)且被这点平分的弦所在的直线方程是___________。
11. △ABC的两个顶点坐标分别是B(0,6)和C(0,-6),另两边AB、AC的斜率的乘积是- ,求顶点A的轨迹方程。
,求顶点A的轨迹方程。
12. 在面积为1的△PMN中,tanM= ,tanN=-2,建立适当的坐标系,求出以M、N为焦点并且过点P的椭圆方程。
,tanN=-2,建立适当的坐标系,求出以M、N为焦点并且过点P的椭圆方程。
[参考答案]
1. 解析:将方程x2+ky2=2化为椭圆的标准方程为 =1,又焦点在y轴上,
=1,又焦点在y轴上,
∴ >2,解之得0<k<1。
>2,解之得0<k<1。
2. 解析:由椭圆方程知a=5,|CF1|+|CF2|=2a=10,|DF1|+|DF2|=2a=10,则△F2CD的周长|F2C|+|F2D|+|CD|=|CF1|+|CF2|+|DF1|+|DF2|=10+10=20。
3. 解析:由椭圆的标准方程易知c=3,不妨设F1(-3,0)、F2(3,0),因为线段PF1的中点在y轴上,由中点坐标公式知xP=3,由椭圆方程 =1解得yp=±
=1解得yp=± ,故M点纵坐标为±
,故M点纵坐标为± 。
。
4. 解析:从方程中可得a=3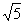 ,b=2
,b=2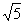 ,c=5
,c=5
∵|PF1|+|PF2|=2a=6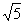 ,∴(|PF1|+|PF2|)2=180
,∴(|PF1|+|PF2|)2=180
即|PF1|2+|PF2|2+2|PF1|·|PF2|=180
由已知PF1⊥PF2,∴|PF1|2+|PF2|2=(2c)2=100代入上式得2|PF1|·|PF2|=80
∴(|PF1|-|PF2|)2=|PF1|2+|PF2|2-2|PF1|·|PF2|=20
∴||PF1|-|PF2||=2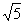
答案:B
5. 解析:设A(x1,y1),B(x2,y2)
由方程组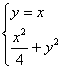 得
得 =1
=1
∴x=±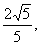 y=±
y=± ,
,
即A( ),B(-
),B(- ,-
,- )
)
由两点间距离公式可得|AB|=
6. 解析:设|PF1|=m,|PF2|=n,
在△F1PF2中,由余弦定理有m2+n2-2mncos60°=|F1F2|2=122,即m2+n2-mn=144 ①
由椭圆定义知m+n=20,则m2+n2+2mn=400 ②
由②-①得,3mn=256,故mn=
因此,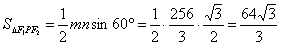
7. 解析:如图所示,设B、C为B′C′的两个三等分点,则B′(-24,0),C′(24,0),连接AB′,AC′,设A(x,y),BM、CN又分别为△ACB′与△ABC′的中位线。

∴|AB′|=2|BM|,|AC′|=2|CN|
∴|AB′|+|AC′|=2(|BM|+|CN|)=60
由椭圆定义,动点A到两定点B′、C′的距离的和为定长60,所以点A在以B′、C′为焦点,中心在原点的椭圆上运动。
∵2a=60,∴a=30
由|B′C′|=48,得c=24
∴b2=a2-c2=900-576=324
则点A的轨迹方程是 =1(y≠0)
=1(y≠0)
8. 解析:尽管动点M满足|MF1|+|MF2|=2a=6,但2a=|F1F2|,∴M点轨迹应为F1、F2两点间的线段。
答案:F1、F2两点间的线段
9. 解析:设此椭圆方程为mx2+ny2=1(m>0,n>0,m≠n),把P( ,-4),Q(-
,-4),Q(-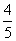 ,3)代入得
,3)代入得
解得m=1,n= ,故椭圆方程为x2+
,故椭圆方程为x2+ =1。
=1。
10. 解析:设弦的两端点分别为A(x1,y1)、B(x2,y2),则有 =1,
=1, =1
=1
两式相减得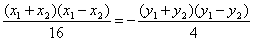
∴
即弦所在直线的斜率为- ,又弦过(2,1)点,故弦所在直线的方程是x+2y-4=0
,又弦过(2,1)点,故弦所在直线的方程是x+2y-4=0
11. 解:设顶点A的坐标为(x,y),由题意得: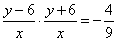
∴顶点A的轨迹方程为: =1(y≠±6)
=1(y≠±6)
12. 解:以直线MN为x轴,以线段MN的中垂线为y轴建立平面直角坐标系,如图所示。

设所求椭圆方程为 =1(a>b>0),分别记M、N、P点的坐标为(-c,0)、(c,0)和(x0,y0)
=1(a>b>0),分别记M、N、P点的坐标为(-c,0)、(c,0)和(x0,y0)
∵tanα=tan(π-∠N)=2
∴由题设知 解得
解得 即 P
即 P
在△MNP中,|MN|=2c,MN上的高为 ,
,
∴S△MNP= =1,解得c=
=1,解得c=
即P( ),由此得|PM|=
),由此得|PM|= ,|PN|=
,|PN|=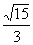
∴a= (|PM|+|PN|)=
(|PM|+|PN|)= ,从而b2=a2-c2=3故所求的椭圆方程为
,从而b2=a2-c2=3故所求的椭圆方程为 =1
=1
-
椭圆的几何性质知识点归纳及典型例题及练习(付答案)
一椭圆的定义1椭圆的定义平面内与两个定点F1F2的距离之和等于定长大于F1F2的点的轨迹叫做椭圆这两个定点F1F2叫做椭圆的焦点两…
-
椭圆的简单几何性质典型例题
例1椭圆的一个顶点为A20其长轴长是短轴长的2倍求椭圆的标准方程分析题目没有指出焦点的位置要考虑两种位置解1当A20为长轴端点时a…
-
椭圆的简单几何性质
82椭圆的简单几何性质一知识点通过对椭圆标准方程的讨论掌握椭圆的性质范围对称性顶点离心率并能正确画出椭圆的图形二能力训练点结合对椭…
-
椭圆的简单几何性质习题
学业水平训练1已知椭圆的长轴长是短轴长的2倍则椭圆的离心率等于1AB3313CD2222解析选D由题意知2a4b又bac233得到…
-
《椭圆的简单几何性质》教学反思
椭圆的简单几何性质教学反思椭圆的简单几何性质的重点是性质难点是应用椭圆的简单几何性质的知识是解析几何中一个重要内容是训练学生逻辑思…
-
椭圆的简单几何性质典型例题
例1椭圆的一个顶点为A20其长轴长是短轴长的2倍求椭圆的标准方程分析题目没有指出焦点的位置要考虑两种位置解1当A20为长轴端点时a…
-
椭圆的简单几何性质
82椭圆的简单几何性质一知识点通过对椭圆标准方程的讨论掌握椭圆的性质范围对称性顶点离心率并能正确画出椭圆的图形二能力训练点结合对椭…
-
椭圆的简单几何性质习题
学业水平训练1已知椭圆的长轴长是短轴长的2倍则椭圆的离心率等于1AB3313CD2222解析选D由题意知2a4b又bac233得到…
-
《椭圆的简单几何性质》教学反思
椭圆的简单几何性质教学反思椭圆的简单几何性质的重点是性质难点是应用椭圆的简单几何性质的知识是解析几何中一个重要内容是训练学生逻辑思…
-
椭圆的几何性质含答案
椭圆的几何性质一选择题本大题共12小题每小题5分共60分在每小题给出的四个选项中只有一项是符合题目要求的1设定点F103F203动…
-
人教A版选修1-1同步练习:2.1椭圆《椭圆的几何性质》(含答案)
备课大师免费备课第一站椭圆的几何性质测试题班级姓名一选择题本大题共12小题每小题5分共60分在每小题给出的四个选项中只有一项是符合…