高数知识点总结(上册)
高数知识点总结(上册)
函数:
绝对值得性质:
(1)|a+b|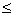 |a|+|b| (2)|a-b|
|a|+|b| (2)|a-b|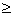 |a|-|b| (3)|ab|=|a||b| (4)|
|a|-|b| (3)|ab|=|a||b| (4)|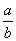 |=
|=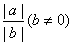
函数的表示方法:
(1)表格法 (2)图示法 (3)公式法(解析法)
函数的几种性质:
(1)函数的有界性 (2)函数的单调性
(3)函数的奇偶性 (4)函数的周期性
反函数:
定理:如果函数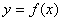 在区间[a,b]上是单调的,则它的反函数
在区间[a,b]上是单调的,则它的反函数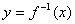 存在,且是单值、单调的。
存在,且是单值、单调的。
基本初等函数:
(1)幂函数 (2)指数函数
(3)对数函数 (4)三角函数
(5)反三角函数
复合函数的应用
极限与连续性:
数列的极限:
定义:设 是一个数列,a是一个定数。如果对于任意给定的正数
是一个数列,a是一个定数。如果对于任意给定的正数 (不管它多么小),总存在正整数N,使得对于n>N的一切
(不管它多么小),总存在正整数N,使得对于n>N的一切 ,不等式
,不等式 都成立,则称数a是数列
都成立,则称数a是数列 的极限,或称数列
的极限,或称数列 收敛于a,记做
收敛于a,记做 ,或
,或 (
( )
)
收敛数列的有界性:
定理:如果数列 收敛,则数列
收敛,则数列 一定有界
一定有界
推论:(1)无界一定发散(2)收敛一定有界 (3)有界命题不一定收敛
函数的极限:
定义及几何定义
函数极限的性质:
(1)同号性定理:如果 ,而且A>0(或A<0),则必存在
,而且A>0(或A<0),则必存在 的某一邻域,当x在该邻域内(点
的某一邻域,当x在该邻域内(点 可除外),有
可除外),有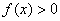 (或
(或 )。
)。
(2)如果 ,且在
,且在 的某一邻域内(
的某一邻域内( ),恒有
),恒有 (或
(或 ),则
),则 (
( )。
)。
(3)如果 存在,则极限值是唯一的
存在,则极限值是唯一的
(4)如果 存在,则在
存在,则在 在点
在点 的某一邻域内(
的某一邻域内( )是有界的。
)是有界的。
无穷小与无穷大:
注意:无穷小不是一个很小的数,而是一个以零位极限的变量。但是零是可作为无穷小的唯一的常数,因为如果 则对任给的
则对任给的 ,总有
,总有 ,即常数零满足无穷小的定义。除此之外,任何无论多么小的数,都不满足无穷小的定义,都不是无穷小。
,即常数零满足无穷小的定义。除此之外,任何无论多么小的数,都不满足无穷小的定义,都不是无穷小。
无穷小与无穷大之间的关系:
(1)如果函数 为无穷大,则
为无穷大,则 为无穷小
为无穷小
(2)如果函数 为无穷小,且
为无穷小,且 ,则
,则 为无穷大
为无穷大
具有极限的函数与无穷小的关系:
(1)具有极限的函数等于极限值与一个无穷小的和
(2)如果函数可表为常数与无穷小的和,则该常数就是函数的极限
关于无穷小的几个性质:
定理:
(1)有限个无穷小的代数和也是无穷小
(2)有界函数 与无穷小a的乘积是无穷小
与无穷小a的乘积是无穷小
推论:
(1)常数与无穷小的乘积是无穷小
(2)有限个无穷小的乘积是无穷小
极限的四则运算法则:
定理:两个函数 、
、 的代数和的极限等于它们的极限的代数和
的代数和的极限等于它们的极限的代数和
两个函数 、
、 乘积的极限等于它们的极限的乘积
乘积的极限等于它们的极限的乘积
极限存在准则与两个重要极限:
准则一(夹挤定理)
设函数 、
、 、
、 在
在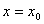 的某个邻域内(点
的某个邻域内(点 可除外)满足条件:
可除外)满足条件:
(1)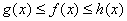
(2) ,
,
则
准则二 单调有界数列必有极限
定理:如果单调数列有界,则它的极限必存在
重要极限:
(1)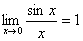 (2)
(2)
(3) 或
或
无穷小阶的定义:
设 为同一过程的两个无穷小。
为同一过程的两个无穷小。
(1)如果 ,则称
,则称 是比
是比 高阶的无穷小,记做
高阶的无穷小,记做
(2)如果 ,则称
,则称 是比
是比 低阶的无穷小
低阶的无穷小
(3)如果 ,则称
,则称 与
与 是同阶无穷小
是同阶无穷小
(4)如果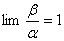 ,则称
,则称 与
与 是等阶无穷小,记做
是等阶无穷小,记做
几种等价无穷小:
对数函数中常用的等价无穷小:
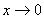 时,
时,

三角函数及反三角函数中常用的等价无穷小:
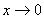 时,
时,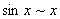




指数函数中常用的等价无穷小:
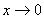 时,
时,

二项式中常用的等价无穷小:
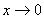 时,
时,

函数在某一点处连续的条件:
由连续定义 可知,函数
可知,函数 在点
在点 处连续必须同时满足下列三个条件:
处连续必须同时满足下列三个条件:
(1) 在点
在点 处有定义
处有定义
(2)当 时,
时, 的极限
的极限 存在
存在
(3)极限值等于函数 在点
在点 处的函数值
处的函数值
极限与连续的关系:
如果函数 在点
在点 处连续,由连续定义可知,当
处连续,由连续定义可知,当 时,
时, 的极限一定存在,反之,则不一定成立
的极限一定存在,反之,则不一定成立
函数的间断点:
分类:第一类间断点 (左右极限都存在) 第二类间断点(有一个极限不存在)
连续函数的和、差、积、商的连续性:
定理:如果函数 、
、 在点
在点 处连续,则他们的和、差、积、商(分母不为零)在点
处连续,则他们的和、差、积、商(分母不为零)在点 也连续
也连续
反函数的连续性:
定理:如果函数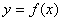 在某区间上是单调增(或单调减)的连续函数,则它的反函数
在某区间上是单调增(或单调减)的连续函数,则它的反函数 也在对应的区间上是单调增(或单调减)的连续函数
也在对应的区间上是单调增(或单调减)的连续函数
最大值与最小值定理:
定理:设函数 在闭区间
在闭区间 上连续,则函数
上连续,则函数 在闭区间
在闭区间 上必有最大值和最小值
上必有最大值和最小值
推论:如果函数 在闭区间
在闭区间 上连续,则
上连续,则 在
在 上有界
上有界
介值定理:
定理:设函数 在闭区间
在闭区间 上连续,两端点处的函数值分别为
上连续,两端点处的函数值分别为 ,而
,而 是介于A与B之间的任一值,则在开区间
是介于A与B之间的任一值,则在开区间 内至少有一点
内至少有一点 ,使得
,使得


推论(1):在闭区间上连续函数必能取得介于最大值与最小值之间的任何值
推论(2):设函数 在闭区间
在闭区间 上连续,且
上连续,且 (两端点的函数值异号),则在
(两端点的函数值异号),则在 的内部,至少存在一点
的内部,至少存在一点 ,使
,使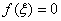
导数与微分
导数:
定义:
导数的几何定义:函数在图形上表示为切线的斜率
函数可导性与连续性之间的表示:
如果函数在x处可导,则在点x处连续,也即函数在点x处连续
一个数在某一点连续,它却不一定在该点可导
据导数的定义求导:
(1)
(2)
(3)
基本初等函数的导数公式:
(1)常数导数为零 
(2)幂函数的导数公式 
(3)三角函数的导数公式



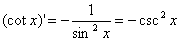


(4)对数函数的导数公式: 
(5)指数函数的导数公式: 
(6)
(7)反三角函数的导数公式:




函数和、差、积、商的求导法则:
法则一(具体内容见书106) 

函数乘积的求导法则:
法则二(具体内容见书108) 
函数商的求导法则:
法则三(具体内容见书109) 
复合函数的求导法则:(定理见书113页)
反函数的求导法则:
反函数的导数等于直接函数导数的倒数
基本初等函数的导数公式:(见书121页)
高阶导数:二阶和二阶以上的导数统称为高阶导数 
求n阶导数:(不完全归纳法)

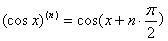
隐函数的导数:(见书126页)
对隐函数求导时,首先将方程两端同时对自变量求导,但方程中的y是x的函数,它的导数用记号 (或
(或 表示)
表示)
对数求导法:先取对数,后求导(幂指函数)
由参数方程所确定的函数的导数:

微分概念:
函数可微的条件
如果函数 在点
在点 可微,则
可微,则 在点
在点 一定可导
一定可导
函数 在点
在点 可微的必要充分条件是函数
可微的必要充分条件是函数 在点
在点 可导
可导

函数的微分dy是函数的增量 的线性主部(当
的线性主部(当 ),从而,当
),从而,当 很小时,有
很小时,有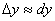
通常把自变量x的增量 称为自变量的微分,记做dx。即于是函数的微分可记为
称为自变量的微分,记做dx。即于是函数的微分可记为 ,从而有
,从而有
基本初等函数的微分公式:
几个常用的近似公式:


 (x用弧度)
(x用弧度) 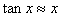 (x用弧度)
(x用弧度)


中值定理与导数应用
罗尔定理:如果函数 满足下列条件
满足下列条件
(1)在闭区间 上连续
上连续
(2)在开区间 内具有导数
内具有导数
(3)在端点处函数值相等,即 ,则在
,则在 内至少有一点
内至少有一点 ,使
,使
拉格朗日中值定理:如果函数 满足下列条件
满足下列条件
(1)在闭区间 上连续
上连续
(2)在开区间 内具有导数,则在
内具有导数,则在 内至少有一点
内至少有一点 ,使得
,使得
定理几何意义是:如果连续曲线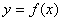 上的弧
上的弧 除端点处外处处具有不垂直于x轴的切线,那么,在这弧上至少有一点c,使曲线在点c的切线平行于弧
除端点处外处处具有不垂直于x轴的切线,那么,在这弧上至少有一点c,使曲线在点c的切线平行于弧
推论:如果函数 在区间
在区间 内的导数恒为零,那么
内的导数恒为零,那么 在
在 内是一个常数
内是一个常数
柯西中值定理:如果函数 与
与 满足下列条件
满足下列条件
(1)在闭区间 上连续
上连续
(2)在开区间 内具有导数
内具有导数
(3)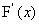 在
在 内的每一点处均不为零,则在
内的每一点处均不为零,则在 内至少有一点
内至少有一点 使得
使得
罗尔定理是拉格朗日中值定理的特例,柯西中值定理是拉格朗日中值定理的推广
洛必达法则:(理论根据是柯西中值定理)
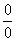 未定式
未定式
1、 情形
情形
定理:如果 (1)当 时,
时, 与
与 都趋于零
都趋于零
(2)在点a的某领域(点a可除外)内, 与
与 都存在且
都存在且
(3)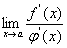 存在(或为
存在(或为 ),则极限
),则极限 存在(或为
存在(或为 ),且
),且 =
=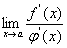
在一定条件下通过分子、分母分别求导数再求极限来确定未定式的值的方法称为洛必达法则
2、 情形
情形
推论:如果 (1)当 时,
时, 与
与 都趋于零
都趋于零
(2)当|x|>N时, 与
与 都存在且
都存在且
(3) 存在(或为
存在(或为 ),则极限
),则极限 存在(或为
存在(或为 ),且
),且 =
=
 未定式
未定式
1、 情形
情形
如果 (1) 时,
时, 与
与 都趋于无穷大
都趋于无穷大
(2)在点a的某领域(点a可除外)内, 与
与 都存在且
都存在且
(3)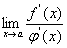 存在(或为
存在(或为 ) ,则则极限
) ,则则极限 存在(或为
存在(或为 ),且
),且 =
=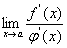
2、 情形
情形
推论:如果 (1) 时,
时, 与
与 都趋于无穷大
都趋于无穷大
(2)当|x|>N时, 与
与 都存在且
都存在且
(3)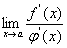 存在(或为
存在(或为 ) ,则则极限
) ,则则极限 存在(或为
存在(或为 ),且
),且 =
=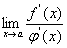
注意:1、洛必达法则仅适用于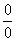 型及
型及 型未定式
型未定式
2、当 不存在时,不能断定
不存在时,不能断定 不存在,此时不能应用洛必达法则
不存在,此时不能应用洛必达法则
泰勒公式(略)
迈克劳林公式(略)
函数单调性的判别法:
必要条件:设函数 在
在 上连续,在
上连续,在 内具有导数,如果
内具有导数,如果 在
在 上单调增加(减少),则在
上单调增加(减少),则在 内,
内,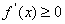 (
( )
)
充分条件:设函数 在
在 上连续,在
上连续,在 内具有导数,
内具有导数,
(1)如果在 内,
内, ,则
,则 在
在 上单调增加
上单调增加
(2)如果在 内,
内, ,则
,则 在
在 上单调减少
上单调减少
函数的极值及其求法
极值定义(见书176页)
极值存在的充分必要条件
必要条件:设函数 在点
在点 处具有导数,且在点
处具有导数,且在点 处取得极值,则
处取得极值,则
函数的极值点一定是驻点
导数不存在也可能成为极值点
驻点:使 的点,称为函数
的点,称为函数 的驻点
的驻点
充分条件(第一):设连续函数 在点
在点 的一个邻域(
的一个邻域( 点可除外)内具有导数,当x由小增大经过
点可除外)内具有导数,当x由小增大经过 时,如果
时,如果
(1) 由正变负,则
由正变负,则 是极大点
是极大点
(2) 由负变正,则
由负变正,则 是极小点
是极小点
(3) 不变号,则
不变号,则 不是极值点
不是极值点
充分条件(第二):设函数 在点
在点 处具有二阶导数,且
处具有二阶导数,且 ,
,
(1)如果 ,则
,则 在
在 点处取得极大值
点处取得极大值
(2)如果 ,则
,则 在
在 点处取得极小值
点处取得极小值
函数的最大值和最小值(略)
曲线的凹凸性与拐点:
定义:设 在
在 上连续,如果对于
上连续,如果对于 上的任意两点
上的任意两点 、
、 恒有
恒有 ,则称
,则称 在
在 上的图形是(向上)凹的,反之,图形是(向上)凸的。
上的图形是(向上)凹的,反之,图形是(向上)凸的。
判别法:
定理:设函数 在
在 上连续,在
上连续,在 内具有二阶导数
内具有二阶导数
(1)如果在 内
内 ,那么
,那么 的图形在
的图形在 上是凹的
上是凹的
(2)如果在 内
内 ,那么
,那么 的图形在
的图形在 上是凸的
上是凸的
拐点:凸弧与凹弧的分界点称为该曲线的拐点。
不定积分
原函数:如果在某一区间上,函数 与
与 满足关系式:
满足关系式:
 或
或 ,则称在这个区间上,函数
,则称在这个区间上,函数 是函数
是函数 的一个原函数
的一个原函数
结论:如果函数 在某区间上连续,则在这个区间上
在某区间上连续,则在这个区间上 必有原函数
必有原函数
定理:如果函数 是
是 的原函数,则
的原函数,则 (C为任意常数)也是
(C为任意常数)也是 的原函数,且
的原函数,且 的任一个原函数与
的任一个原函数与 相差为一个常数
相差为一个常数
不定积分的定义:
定义:函数 的全体原函数称为
的全体原函数称为 的不定积分,记做
的不定积分,记做
不定积分的性质:
性质一: 或
或
及 或
或
性质二:有限个函数的和的不定积分等于各个函数的不定积分的和。即

性质三:被积函数中不为零的常数因子可以提到积分号外面来,即
 (k为常数,且k
(k为常数,且k 0
0
基本积分表:
(1) (k是常数) (2)
(k是常数) (2)
(3)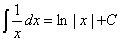 (4)
(4)
(5) (6)
(6)
(7) (8)
(8)
(9) (10)
(10)
(11) (12)
(12)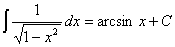
(13)
第一类换元法(凑微分法)



第二类换元法:变量代换
被积函数若函数有无理式,一般情况下导用第二类换元法。将无理式化为有理式
基本积分表添加公式:
结论:
如果被积函数含有 ,则进行变量代换
,则进行变量代换 化去根式
化去根式
如果被积函数含有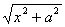 ,则进行变量代换
,则进行变量代换 化去根式
化去根式
如果被积函数含有 ,则进行变量代换
,则进行变量代换 化去根式
化去根式
分部积分法:
对应于两个函数乘积的微分法,可推另一种基本微分法---------分部积分法
 分部积分公式
分部积分公式
1、如果被积函数是幂函数与 的积,可以利用分部积分法
的积,可以利用分部积分法
令u等于幂函数
2、如果被积函数是幂函数与 的积,可使用分部积分法
的积,可使用分部积分法
令u=
3、如果被积函数是指数函数与三角函数的积,也可用分部积分法。
定积分
定积分的定义
定理:如果函数 在
在 上连续,则
上连续,则 在
在 上可积
上可积
定理:如果函数在 上只有有限个第一类间断点,则
上只有有限个第一类间断点,则 在
在 上可积
上可积
定积分的几何意义:
1、在 上
上 ,这时
,这时 的值在几何上表示由曲线
的值在几何上表示由曲线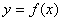 、x轴及二直线x=a、x=b所围成的曲边梯形的面积
、x轴及二直线x=a、x=b所围成的曲边梯形的面积
2、在 上
上 ,其表示曲边梯形面积的负值
,其表示曲边梯形面积的负值
3、在 上,
上, 既取得正值又取得负值
既取得正值又取得负值
几何上表示由曲线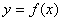 、x轴及二直线x=a、x=b所围成平面图形位于x轴上方部分的面积减去x轴下方部分的面积
、x轴及二直线x=a、x=b所围成平面图形位于x轴上方部分的面积减去x轴下方部分的面积
定积分的性质:
性质一、函数和(差)的定积分等于他们的定积分的和(差),即
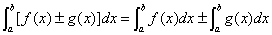
性质二、被积函数中的常数因子可以提到积分号外面,即
 (k是常数)
(k是常数)
性质三、如果将区间 分成两部分
分成两部分 和
和 ,那么
,那么
 、
、
性质四、如果在 上,
上, ,那么
,那么
性质五、如果在 上,
上, ,那么
,那么
性质六、如果在 上,
上, ,那么
,那么

性质七、设M及m,分别是函数 在区间
在区间 上的最大值及最小值,则
上的最大值及最小值,则
m(b-a) M(b-a) (a
M(b-a) (a
性质八、积分中值定理
如果函数 在闭区间
在闭区间 上连续,那么在积分区间
上连续,那么在积分区间 上至少有一点
上至少有一点 ,使得
,使得
微积分基本公式
积分上限的函数: (a
(a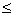 x
x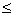 b)
b)
性质:如果函数 在区间
在区间 上连续,那么积分上限的函数
上连续,那么积分上限的函数 在
在 上具有导数,且
上具有导数,且
定理:在区间 上的连续函数
上的连续函数 的原函数一定存在
的原函数一定存在
牛顿——莱布尼茨公式
如果函数 在区间
在区间 上连续,且
上连续,且 是
是 的任意一个原函数,那么
的任意一个原函数,那么
定积分的换元法
假设(1)函数 在区间
在区间 上连续;
上连续;
(2)函数 在区间
在区间 上单值,且具有连续导数;
上单值,且具有连续导数;
(3)当t在区间 上变化时,
上变化时, 的值在
的值在 上变化,且
上变化,且 ,
, ,则有定积分的换元公式
,则有定积分的换元公式
设 在区间
在区间 上连续,则
上连续,则
(1)如果函数 为奇函数,则
为奇函数,则
(2)如果函数 为偶函数,则
为偶函数,则

定积分的分部积分法
设 、
、 在
在 上具有连续导数
上具有连续导数 、
、 ,那么
,那么 ,在等式的两边分别求a到b的定积分得
,在等式的两边分别求a到b的定积分得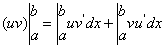 ……定积分的分部积分公式
……定积分的分部积分公式
即 或
或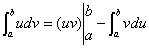
无穷区间上的广义积分
定义:设函数 在区间
在区间 上连续,取b>a,如果极限
上连续,取b>a,如果极限 存在,则称此极限为函数
存在,则称此极限为函数 在区间
在区间 上的广义积分,记做
上的广义积分,记做 即
即
无界函数的广义积分(见书279页)
定积分的应用(见书286页)
元素法 在极坐标系中的计算法
-
高一数学上册基础知识点总结
珠晖区青少年活动中心中学部博学教育培训中心必修一基础要点归纳第一章集合与函数的概念一集合的概念与运算1集合的特性与表示法集合中的元…
-
高一数学上册知识点
高一数学知识总结必修一一、集合一、集合有关概念集合的含义集合的中元素的三个特性:元素的确定性如:世界上最高的山元素的互异性如:由H…
-
高一数学上册基础知识点总结
珠晖区青少年活动中心中学部博学教育培训中心必修一基础要点归纳第一章集合与函数的概念一集合的概念与运算1集合的特性与表示法集合中的元…
-
高一数学上册基础知识点总结(1)
珠晖区青少年活动中心中学部博学教育培训中心必修一基础要点归纳第一章集合与函数的概念一集合的概念与运算1集合的特性与表示法集合中的元…
-
高一数学上册基础知识点总结
必修一基础要点归纳第一章.集合与函数的概念一、集合的概念与运算:1、集合的特性与表示法:集合中的元素应具有:确定性互异性无序性;集…
-
高数上册知识点总结
高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(y?ax),三…
-
同济六版上册高数总结(一些重要公式及知识点)
同济六版上册高数总结微分公式与积分公式(tgx)??secx(ctgx)???csc2x(secx)??secx?tgx(cscx…
-
高等数学中易错知识点总结
1.在一元函数中,若函数在某点连续,则该函数在该点必有极限。若函数在某点不连续,则该函数在该点必无极限。2,在一元函数中,若函数在…
-
考研数学高等数学知识点总结:渐近线
考研数学高等数学知识点总结:渐近线来源:文都教育一、知识点复习1.水平渐近线如果x??x???x???limf(x)?b,则曲线y…
-
高等数学知识点总结
高等数学知识点总结导数公式2tanxsecxctanxcscxsecxsecxtanxcscxcscxcotxaalnalogax…
-
《高等数学》 各章知识点总结——第9章
第9章多元函数微分学及其应用总结一、多元函数的极限与连续1、n维空间R2为二元数组(x,y)的全体,称为二维空间。R3为三元数组(…