数列方法与技巧总结
数列方法与技巧总结
1.an={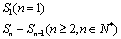 注意验证a1是否包含在an 的公式中.
注意验证a1是否包含在an 的公式中.
2.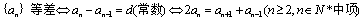
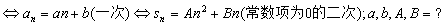
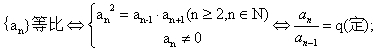
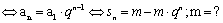
如若 是等比数列,且
是等比数列,且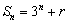 ,则
,则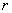 = (答:-1)
= (答:-1)
3.首项正的递减(或首项负的递增)等差数列前n项和最大(或最小)问题,转化为解不等式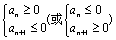 ,或用二次函数处理;(等比前n项积?),由此你能求一般数列中的最大或最小项吗?
,或用二次函数处理;(等比前n项积?),由此你能求一般数列中的最大或最小项吗?
如(1)等差数列 中,
中, ,
,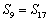 ,问此数列前多少项和最大?并求此最大值.(答:前13项和最大,最大值为169);
,问此数列前多少项和最大?并求此最大值.(答:前13项和最大,最大值为169);
(2)若 是等差数列,首项
是等差数列,首项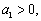
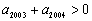 ,
,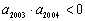 ,则使前n项和
,则使前n项和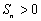 成立的最大正整数n是 (答:4006)
成立的最大正整数n是 (答:4006)
4.等差数列中an=a1+(n-1)d;Sn=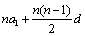 =
=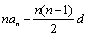 =
=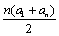
等比数列中an= a1 qn-1;当q=1,Sn=na1 当q≠1,Sn=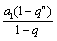 =
=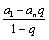
5.常用性质:等差数列中, an=am+ (n-m)d, 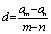 ;当m+n=p+q,am+an=ap+aq;
;当m+n=p+q,am+an=ap+aq;
等比数列中,an=amqn-m; 当m+n=p+q ,aman=apaq;
如(1)在等比数列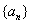 中,
中,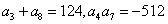 ,公比q是整数,则
,公比q是整数,则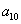 =___(答:512);
=___(答:512);
(2)各项均为正数的等比数列 中,若
中,若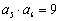 ,则
,则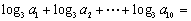 (答:10).
(答:10).
6.常见数列:{an}、{bn}等差则{kan+tbn}等差;
{an}、{bn}等比则{kan}(k≠0)、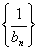 、{anbn}、
、{anbn}、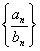 等比;
等比;
{an}等差,则 (c>0)成等比.
(c>0)成等比.
{bn}(bn>0)等比,则{logcbn}(c>0且c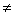 1)等差.
1)等差.
7.等差三数为a-d,a,a+d;四数a-3d,a-d,,a+d,a+3d;
等比三数可设a/q,a,aq;四个数成等比的错误设法:a/q3,a/q,aq,aq3 (为什么?)
如有四个数,其中前三个数成等差数列,后三个成等比数列,且第一个数与第四个数的和是16,第二个数与第三个数的和为12,求此四个数.(答:15,,9,3,1或0,4,8,16)
8. 等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列.
等比数列{an}的任意连续m项的和且不为零时构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列.
如:公比为-1时, 、
、 -
- 、
、 -
- 、…不成等比数列
、…不成等比数列
9.等差数列{an},项数2n时,S偶-S奇=nd;项数2n-1时,S奇-S偶=an ;
等比数列{an},项数为 时,则
时,则 ;项数为奇数
;项数为奇数 时,
时, .
.
10.求和常法:公式、分组、裂项相消、错位相减、倒序相加.关键找通项结构.
分组法求数列的和:如an=2n+3n 、错位相减法求和:如an=(2n-1)2n、裂项法求和:如求和: (答:
(答: )、
)、
倒序相加法求和:如①求证: ;②已知
;②已知 ,则
,则 =___(答:
=___(答: )
)
11.求数列{an}的最大、最小项的方法(函数思想):
①an+1-an=…… 如an= -2n2+29n-3 ②
如an= -2n2+29n-3 ② (an>0) 如an=
(an>0) 如an= ③ an=f(n) 研究函数f(n)的增减性 如an=
③ an=f(n) 研究函数f(n)的增减性 如an=
求通项常法:
(1)已知数列的前n项和 ,求通项
,求通项 ,可利用公式:
,可利用公式:
如:数列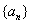 满足
满足 ,求
,求 (答:
(答: )
)
(2)先猜后证
(3)递推式为 =
= +f(n) (采用累加法);
+f(n) (采用累加法); =
= ×f(n) (采用累积法);
×f(n) (采用累积法);
如已知数列 满足
满足 ,
,
 ,则
,则 =________
=________
(答: )
)
(4)构造法形如 、
、 (
( 为常数)的递推数列如①已知
为常数)的递推数列如①已知 ,求
,求 (答:
(答: );
);
(5)涉及递推公式的问题,常借助于“迭代法”解决,适当注意以下公式的合理运用 : an=(an-an-1)+(an-1-an-2)+……+(a2-a1)+a1 ;
an=
(6)倒数法形如 的递推数列都可以用倒数法求通项.如
的递推数列都可以用倒数法求通项.如
①已知 ,求
,求 (答:
(答: );
);
②已知数列满足 =1,
=1, ,求
,求 (答:
(答: )
)
12.常见和: ,
,  ,
,

13. 若等差数列 的首项是
的首项是 ,公差是
,公差是 ,则
,则 .
.
通项公式的变形:① ;②
;② ;③
;③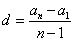 ;④
;④ ;⑤
;⑤ .
.
等差数列的前 项和的公式:①
项和的公式:① ;②
;② .
.
14.若等比数列 的首项是
的首项是 ,公比是
,公比是 ,则
,则 .
.
通项公式的变形:①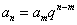 ;②
;② ;③
;③ ;④
;④
等比数列 的前
的前 项和的公式:
项和的公式: .
.
 时,
时, ,即常数项与
,即常数项与 项系数互为相反数
项系数互为相反数
第二篇:【方法总结】由递推式求数列通项典型例题的技巧解法
由递推式求数列通项的典型题的技巧解法
对于由递推公式确定的数列的求解,通常可以通过递推公式的变换转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列。
类型1 递推公式为
解法:把原递推公式转化为 ,利用累加法(逐差相加法)求解。
,利用累加法(逐差相加法)求解。
例1. 已知数列 满足
满足 ,
, ,求数列
,求数列 的通项公式。
的通项公式。
解:由条件知:
分别令 ,代入上式得
,代入上式得 个等式累加之,即
个等式累加之,即

所以
 ,
,
类型2 (1)递推公式为
解法:把原递推公式转化为 ,利用累乘法(逐商相乘法)求解。
,利用累乘法(逐商相乘法)求解。
例2. 已知数列 满足
满足 ,
, ,求数列
,求数列 的通项公式。
的通项公式。
解:由条件知 ,分别令
,分别令 ,代入上式得
,代入上式得 个等式累乘之,即
个等式累乘之,即



又 ,
,
(2)由 和
和 确定的递推数列
确定的递推数列 的通项可如下求得:
的通项可如下求得:
由已知递推式有 ,
,  ,
, ,
, 依次向前代入,得
依次向前代入,得 ,
,
简记为
 ,这就是叠(迭)代法的基本模式。
,这就是叠(迭)代法的基本模式。
(3)递推式:
解法:只需构造数列 ,消去
,消去 带来的差异。
带来的差异。
例3.设数列 :
: ,求数列
,求数列 的通项公式。
的通项公式。
解:设 ,将
,将 代入递推式,得
代入递推式,得




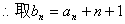 …(1)则
…(1)则 ,又
,又 ,故
,故 代入(1)得
代入(1)得
说明:(1)若 为
为 的二次式,则可设
的二次式,则可设 ;
;
(2)本题也可由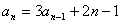 ,
, (
( )
)
两式相减得 转化为
转化为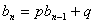 求之.
求之.
例4.已知 ,
,
 ,求数列
,求数列 的通项公式。
的通项公式。
解:

类型3 递推公式为 (其中p,q均为常数,
(其中p,q均为常数, )。
)。
解法:把原递推公式转化为: ,其中
,其中 ,再利用换元法转化为等比数列求解。
,再利用换元法转化为等比数列求解。
在数列 中,若
中,若 ,则该数列的通项
,则该数列的通项
 。
。
例5. 已知数列 中,
中, ,
, ,求数列
,求数列 的通项公式。
的通项公式。
解:设递推公式 可以转化为
可以转化为 即
即 .故递推公式为
.故递推公式为 ,令
,令 ,则
,则 ,且
,且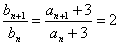 .所以
.所以 是以
是以 为首项,2为公比的等比数列,则
为首项,2为公比的等比数列,则 ,
,
所以 .
.
类型4 递推公式为 (其中p,q均为常数,
(其中p,q均为常数, )。 (或
)。 (或 ,其中p,q, r均为常数)
,其中p,q, r均为常数)
解法:该类型较类型3要复杂一些。一般地,要先在原递推公式两边同除以 ,得:
,得: 。
。
引入辅助数列 (其中
(其中 ),得:
),得: 再应用类型3的方法解决。
再应用类型3的方法解决。
例6. 已知数列 中,
中, ,
, ,求数列
,求数列 的通项公式。
的通项公式。
解:在 两边乘以
两边乘以 得:
得:
令 ,则
,则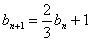 ,应用例7解法得:
,应用例7解法得:
所以 数学驿站:
数学驿站:
类型5 递推公式为 (其中p,q均为常数)。
(其中p,q均为常数)。
解法:先把原递推公式转化为
其中s,t满足 ,再应用前面类型3的方法求解。
,再应用前面类型3的方法求解。
已知数列 满足
满足 求数列
求数列 的通项公式。
的通项公式。
例7. 已知数列 中,
中, ,
, ,
, ,求数列
,求数列 的通项公式。
的通项公式。
解:由 可转化为
可转化为
即
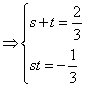
 或
或
这里不妨选用 (当然也可选用
(当然也可选用 ,大家可以试一试),则
,大家可以试一试),则
 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 ,应用类型1的方法,分别令
,应用类型1的方法,分别令 ,代入上式得
,代入上式得 个等式累加之,即
个等式累加之,即

又 ,所以
,所以 。
。
类型6 递推公式为 与
与 的关系式。(或
的关系式。(或 )
)
解法:利用 进行求解。
进行求解。
例8. 已知数列 前n项和
前n项和 ,
,
(1) 求 与
与 的关系;
的关系;
(2) 求数列 的通项公式。
的通项公式。
解:(1)由 得:
得:
于是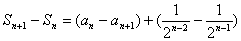
所以
 .
.
(2)应用类型4的方法,上式两边同乘以 得:
得:
由 .于是数列
.于是数列 是以2为首项,2为公差的等差数列,所以
是以2为首项,2为公差的等差数列,所以

类型7 双数列型
解法:根据所给两个数列递推公式的关系,灵活采用累加、累乘、化归等方法求解。
例9. 已知数列 中,
中, ;数列
;数列 中,
中, 。当
。当 时,
时, ,
, ,求数列
,求数列 、
、 的通项公式。
的通项公式。
解:因



所以


即 …………………………………………(1)
…………………………………………(1)
又因为



所以

 ……
……
 .即
.即
 ………………………(2)
………………………(2)
由(1)、(2)得: ,
, 
总结方法比做题更重要!方法产生
于具体数学内容的学习过程中.
-
数列方法总结
1在等差数列(这里即中,当项数为偶数);时,。;项数为奇数时,,如(2)若等差数列、的前和分别为、,且,则.如设{}与{}是两个等…
-
数列方法总结
数列通项公式的求法一定义法直接利用等差数列或等比数列的定义求通项的方法叫定义法这种方法适应于已知数列类型的题目2aSnana1a3…
-
人教版高中数学数列方法总结
数列通项公式的求法一定义法直接利用等差数列或等比数列的定义求通项的方法叫定义法这种方法适应于已知数列类型的题目2anSna1a3a…
-
数列方法与技巧总结
平邑实验中学高三复习阅读材料数列方法与技巧总结数列方法与技巧总结1aSn1n1Sa1是否包含在an的公式中nSn1n2nN注意验证…
-
高中数学数列方法大总结
一、等差数列与等比数列二、等差数列的性质:1若等差等差数列的前n项和为Sn,在d?0时,有最大值.如何确定使Sn取最大值时的n○值…
-
数列方法总结
1在等差数列(这里即中,当项数为偶数);时,。;项数为奇数时,,如(2)若等差数列、的前和分别为、,且,则.如设{}与{}是两个等…