高等数学学习心得

机制1班 陈涛

经过半年的高等数学的学习，对于高等数学有些心得与体会。

首先高等数学是我第一次接触，明显感觉到它与初中及高中时候学习的初等数学有很大的不同。对于初等数学，我们是为了中考以及高考才努力学习，学习初等数学，只需要做大量的习题，熟练解题的步骤，就可以在考试中获得十分可观的分数。但是对于高等数学，我们以前学习初等数学的方法以及认识已经不再适用于高等数学的学习。

学习高等数学是为了诸多研究性专业与学科打好基础，它是研究科学问题的最重要的工具，毫不夸张的说高等数学就是一门研究性的学科，学习高等数学我们要抱着科学严谨的态度。对于高等数学我们要多思考，多理解，从根本上去探索它的定义，它的意义。学习初等数学的题海战术已不再适用于高等数学。如果对于高等数学的某个定义你不理解，做再多的题也很难去寻找这个定义的根本，就算你通过做大量的题熟悉某一类题目的解题方法，但将题目类型稍微改变一下，估计你就无计可施了。所以，我们要从根本上理解它的定义，因为不管题目如何变换，它始终不会离开定义。所以理解定义是学习高等数学的关键，是高等数学的基础。

兴趣也是学习高等数学的关键。学习高等数学必须要有兴趣，很多人说高等数学很难很枯燥，就是因为没有产生兴趣，兴趣是学习最好的导师，只要你有兴趣，那么你自然会努力学习这门课程，就不会感觉到乏味与困难。兴趣是你学习高等数学的动力，有了兴趣你就会勇于在高等数学的海洋中探索。

在这半年的学习中，我们学习了高等数学中的函数、极限、导数、微积分等概念。首先在函数的学习中，我们主要学习了一些关于函数的基本概念以及函数性质。其次，我们学习了极限，在极限的学习过程中，我们学习了两个重要极限以及介值定理。在求极限的过程中我们学习等价替换等方法求极限，为我们解决了求极限问题的障碍。在学习极限之后，我们学习了导数。明白了引出导数的原因，以及导数存在的意义。在导数的学习中，我们学习了隐函数的导数；导数的定义；洛必达法则求极限的方法；求曲线的切线方程；函数的一些利用导数求出的一些性质，例如单调性，凹凸性；微分在近似计算中的应用；麦克劳林公式，中值定理证明以及导数的应用等方面的知识。导数是高等数学非常重要的组成部分，在高等数学中与许多概念都有关联。紧接着导数我们学习的是积分，积分是高等数学重要的组成部分之一，积分是由平面图形的面积提出的，它在物理学中也有极多的应用。在积分的学习中，我们学习许多关于定积分与不定积分概念与计算方法以及（不）定积分中的性质，并且在定积分中有诸多例如奇偶性，周期性等重要性质，这是我们学习的重要部分。在积分中还有一些性质需要我们注意，比如反常积分，变上限积分函数，还有利用积分求极限，还有一点非常重要的应用需要我们注意，利用积分求面积求体积。在这学期最后我们学习了我感觉是本学期最难一部分，微分方程。在课堂听课的过程中我发现了许多同学对这方面的学习与理解有困难，我也感觉到这章的学习比前几章要吃力的多。微分方程这章的定义比较深奥，这是导致许多同学无法理解的重要原因。其次这章的学习过程中，题目的类型过多，以及书本上讲的过于狭隘，我们在计算过程中十分容易碰壁。对于许多题目无从下手。

经过这半年的学习我对数学有了更深刻的认识，数学是最严谨的语言，它只有错与对，永远不会出现模棱两可的概念。数学也是我最喜欢的学科，因为数学题

目会给我惊喜，没当解出一题，自豪与满足感便会充满全身。这般的学习也让我对数学的学习有了更详细的计划，让我对数学的学习有了更浓厚的兴趣。

 

第二篇：高等数学上册学习心得

第三章 中值定理及导数的应用

此章节中主要有：罗尔定理，拉格朗日中值定理，柯西中值定理，洛必达法则，泰勒公式。在这一章中除了要掌握这些定理公式外，还要熟练掌握导数运用的知识。

1．罗尔定理

  如果函数在闭区间内连续，在开区间内可导，且f（a）=f（b），则至少有一点c，使得在该点的导数为0。

罗尔定理是拉格朗日中值定理的特殊情况。

2．拉格朗日中值定理。

  如果函数在闭区间内连续，在开区间内可导，那么 至少有一点c使得f`（c）=f（b）-f（a）/b-a成立。

它的几何意义就是：如果连续曲线的弧AB上除两个端点外处处有不垂直与x轴的切线，那么在弧上至少有一点c，使曲线在该点的切线平行于弦AB。

  拉格朗日中值定理是微分学中的最基本的定理，有着广泛的应用。应用于不等式的证明，

3．柯西中值定理。

  如果函数f（x）及F（X），在开区间内可导，在闭区间内连续，且F`（X）在开区间内处处不为0，那么至少存在一点C使得等式f（b）-f（a）/F（b）-F（a）=f`（C）/F`（C）成立。

注：拉格朗日中值定理是柯西中值定理的特殊情况。

主要应用在书P90。

4．洛必达法则。

  该法则主要用来解决型如0/0,∞/∞这类未定式的极限问题。

如果函数f（x），F（x）满足：

   （1） 当x->a时   f（x），F（x）都趋进于a。

   （2） f`（x），F`（x）在点a的某个去心领域内都存在，且F`（x）不等于0；

   （3） 导数商的极限存在。

      则     函数的极限就是导数商的极限（应该满足三个条件。）详见书P92的定理3.5（当导数商的极限不存在时应采用其他方法求原函数的极限）。

     其他未定式如：0*∞，∞-∞，0的0次方，1的∞次方，∞的0次方，均可转化为0/0，∞/∞型的未定式来计算。转化之后再用“函数的极限就是导数商的极限”。

5．泰勒公式。

  泰勒中值定理：如果函数在含有x的开区间内具有直到（n+1）阶的导数，则当x0在（a，b）内时，f（x）可以表示为（x-x0）的一个n次多项式与余项Rn（x）之和。表达式在书P98。

最基本的形式为f``（x0）/2！*（x-x0）2。

泰勒公式中的余项也称为拉格朗日型余项。

当泰勒展开式中的x0=0时，便得到泰勒公式的简单形式——麦克劳林公式。

▲在这一章中应该熟练掌握泰勒公式的书写及1阶或n阶麦克劳林展开式的书写。

详细介绍在书P99。

6．函数单调性的判别法。

  判定定理：如果函数在闭区间内连续，在开区间内可导，则

         若在开区间上，导数大于0，则函数单调递增。

         若在开区间上，导数小于0，则函数单调递减。

讨论函数单调性的一般步骤是：

（1）    确定函数的定义域。

（2）    求出导数并找出导数为0的点（该点的X值叫做驻点），和导数不存在的点。

（3）    用上述各点将定义域划分为不同的区间，再在各个小区间上判断导数的符号，从而确定函数的单调性。（例题在书P103，例15）

7．函数的极值及其求法。

   极值就是说在定义域范围内一个小区间上的最大值和最小值。

   极值的必要条件：如果函数在x0处可导，且在x0处取得极值，则一定有极限为0。

极值的第一充分条件：设函数在x0的一个领域内可导且导数为0，则：

（1）  如果对x0左侧邻近的点x，有f`（x）大于0，右侧邻近的点x，有f`（x）小于0，则f（x0）是f（x）的极大值。

（2）  如果对x0左侧的邻近点x，有导数小于0，右侧邻近的点x，有导数大于0，则f（x0）是f（x）的极小值。

（3）  如果对x0两侧的点x，其导数恒为正或恒为负，则说明f（x0）不是f（x）的极值。

此定理表明，如果在x0两侧的导数符号相反，则

f（x0）一定是极值，如果x0两侧的导数符号相同，则f（x0）一定不是极值。

极值的第二充分条件：设函数在x0处有二阶导数且f`（x0）=0，f``（x0）不等于0，那么，

（1）  当f``（x0）小于0时，函数在x0处取得极大值。

（2）  当f``（x0）大于0时，函数在x0处取得极小值。

★什么叫做驻点？(它和极值点有关系)

答：极值点的自变量x就是驻点。但是驻点不一定就是极值点的自变量x。

8．函数的最大值和最小值。

   最大值就是在定义域内函数值最大的值，最小值也一样。

★求函数在闭区间上最值的一般方法：

（1）  求出函数在开区间上的全部驻点和导数不存在的点x1，x2，x3，x4等。

（2）  计算并比较f（a），f（x1），f（x2），f（x3），f（x4）……f(b)的大小,其中最大的就是最大值,最小的就是最小值

9.曲线的凹凸与拐点.

设函数在[a,b]上连续,在(a,b)上具有一阶,二阶导数,那么

（1）  若在(a,b)内,二阶导数大于0,则函数在[a,b]上的图形是凹的。

（2）  若在(a,b)内,二阶导数小于0,则函数在[a,b]上的图形是凸的。

注：判断函数图形的凹凸性，应该利用二阶导数大于或小于0来判断。

▲     一般把连续曲线上凹弧与凸弧的分界点称为拐点。在拐点处二阶导数是零。

求拐点的一般方法是：（与高中判断函数单调性的方法差不多）二阶导数为零的点就是拐点。

（1）  求出函数的二阶导数。

（2）  求出二阶导数为0的点，和不存在的点，利用这些点把定义域分为几部分。

（3）  考察二阶导数在各个区间上的符号，从而确定函数的凹凸性及拐点。

例题在书P114，例25，26。

求拐点的方法简介：首先确定函数的定义域，再求出一阶，二阶导数，然后令二阶导数为零求出X1，X2。这两点将定义域分为几部分，分别判断二阶导数的符号。

10．函数图形的描绘

一般步骤是：

（1）  确定函数的定义域。

（2）  求出函数的一阶和二阶导数。

（3）  求出一阶和二阶导数为0的点，和一阶和二阶导数不存在的点，利用这些点来划分区间。列表讨论在各个部分上曲线的升降，凹凸，极值点，拐点。

（4）  如果曲线存在渐近线，则要求出渐近线。

（5）  综合以上结论，与平滑的曲线画出函数的图形。

例题在书P116，例28，29。

▲本章中证明不等式的方法有多种，主要有：

         （1）利用拉格朗日中值定理证明。（对中值进行放缩）例题在书上P90

         （2）利用泰勒中值定理（判断余项的符号）

         （3）利用函数的单调性。

         （4）利用函数的极值与最值。

         （5）利用函数的凹凸性。（理论支持在书P112的定理3.2）.

11．曲率

弧微分公式在书P119的▲部分。

曲率的计算公式：平均曲率的极限就是曲线在点M处的曲率。（△s->0）

平均曲率k=|△a/△s|。其中△a表示切线转过的角度。△s表示增加弧的长度。

经过多次推导可知：曲率的计算公式是

▲     曲率圆与曲率半径.

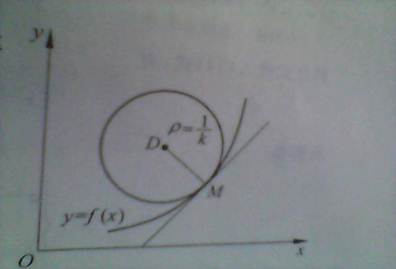
曲率圆的定义:设函数f(x)在M处的曲率为k,在点M处的曲线的法线上,在曲线凹的一侧取一点D,使|DM|=1/k=P,（P表示曲率半径）以D为圆心,DM为半径的圆称为曲线在M处的曲率圆.DM为曲率半径.

注:（1）曲率与曲率半径的关系是:1/k=p。

（2） 曲线与它的曲率圆在同一点处具有相同的切线，曲率，凹向，因此可用曲率圆在带内处的一段圆弧来代替曲线弧。