高等数学极限方法总结
极限
摘要:数列极限的求法一直是数列中一个比较重要的问题, 本文通过归纳和总结, 从不同 的方面罗列了它的几种求法.
关键词:高等数学、数列极限、定义、洛比达法则、
一.引言
高等数学第二章在整个高等数学的学习中都占有相当重要的地位 , 特别是极限,原因就是后续章节本质上都是极限。一个经典的形容就是假如高等数学是棵树木的话,那么极限就是它的根,函数就是它的皮。树没有根,活不下去, 没有皮,只能枯萎,可见极限的重要性。
极限一直是数学分析中的一个重点内容,而对数列极限的求法可谓是多种多样,通过归纳和总结,我们罗列出一些常用的求法。求数列极限的最基本的方法 还是利用数列极限的定义,也要注意运用两个重要极限,其中,可以利用等量代 换,展开、约分,三角代换等方法化成比较好求的数列,也可以利用数列极限的 四则运算法则计算。夹逼性定理和单调有界原理是很重要的定理,在求的时候要 重点注意运用。泰勒公式、洛必达法则、黎曼引理是针对某些特殊的数列而言的。还有一些比较常用的方法,在本文中都一一列举了。
二. 研究问题及成果
一、 极限定义、运算法则和一些结果
1.定义:(各种类型的极限的严格定义参见《高等数学》函授教材,这里不一一叙述)。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如: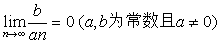 ;
; ;
; ;等等
;等等
(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 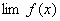 ,
,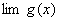 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
(2)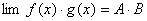
(3)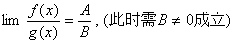
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 
(2)  ;
; 
说明:( 1 )不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式.
(2)一定注意两个重要极限成立的条件。 一定注意两个重要极限
成立的条件。
例如: ,
,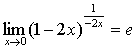 ,
, ;等等。
;等等。
4.洛比达法则
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
 ~
~ ~
~ ~
~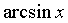 ~
~ ~
~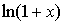 ~
~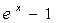 。
。
说明:当上面每个函数中的自变量x换成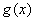 时(
时( ),仍有上面的等价
),仍有上面的等价
关系成立,例如:当 时,
时,  ~
~  ;
; ~
~  。
。
定理4 如果函数 都是
都是 时的无穷小,且
时的无穷小,且 ~
~ ,
,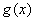 ~
~ ,则当
,则当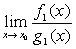 存在时,
存在时, 也存在且等于
也存在且等于
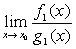 ,即
,即 =
=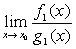 。
。
5.洛比达法则
定理5 假设当自变量x趋近于某一定值(或无穷大)时,函数 和
和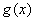 满足:(1)
满足:(1) 和
和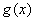 的极限都是0或都是无穷大;
的极限都是0或都是无穷大;
(2) 和
和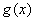 都可导,且
都可导,且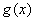 的导数不为0;
的导数不为0;
(3) 存在(或是无穷大);
存在(或是无穷大);
则极限 也一定存在,且等于
也一定存在,且等于 ,即
,即 =
= 。
。
说明:定理5称为洛比达法则,用该法则求极限时,应注意条件是否满足,只要有一条不满足,洛比达法则就不能应用。特别要注意条件(1)是否满足,即验证所求极限是否为“ ”型或“
”型或“ ”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
6.连续性
定理6 一切连续函数在其定义去间内的点处都连续,即如果 是函数
是函数 的定义去间内的一点,则有
的定义去间内的一点,则有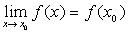 。
。
7.极限存在准则
定理7(准则1) 单调有界数列必有极限。
定理8(准则2) 已知 为三个数列,且满足:
为三个数列,且满足:
(1) 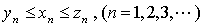
(2)  ,
,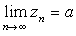
则极限 一定存在,且极限值也是a ,即
一定存在,且极限值也是a ,即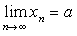 。
。
二、求极限方法举例
1. 利用函数的连续性(定理6)求极限
例4 
解:因为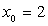 是函数
是函数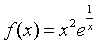 的一个连续点,
的一个连续点,
所以 原式= 。
。
2. 利用两个重要极限求极限
例5 
解:原式= 。
。
注:本题也可以用洛比达法则。
例6 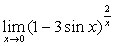
解:原式= 。
。
例7 
解:原式= 。
。
注:两个重要的极限分别为 limsin x 1 2 = 1 和 lim (1 + ) x = e ,对第一个而言是 x→0 x →∞ x xX 趋近 0 时候的 sinx 与 x 比值。第2 个实际上如果 x 趋近无穷大和无穷小都有 对有对应的形式。当底数是 1 的时候要特别注意可能是用第2 个重要极限。
3. 利用定理2求极限
例8 
解:原式=0 (定理2的结果)。
4. 利用等价无穷小代换(定理4)求极限
这种方法的理论基础主要包括:(1)有限个无穷小的和、差、积仍是无穷小.(2)有界函数与无穷小的乘积是无穷小.(3)非零无穷小与无穷大互为倒数.(4)等价无穷小代换(当求两个无穷小之比的极限时,分子与分母都可用等价无穷小代替).[3]
设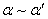 、
、 且
且 ;则:
;则: 与
与 是等价无穷小的充分必要条件为:
是等价无穷小的充分必要条件为: .
.
常用等价无穷小:当变量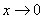 时,
时,

 .
.
例1 求 .
.
解  ,
,
故,原式
例2 求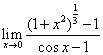 .
.
解  ,因此:
,因此:
原式 .
.
例3 求  .
.
解 
 ,故:原式=
,故:原式=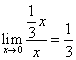 .
.
例4 求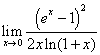 .
.
解  ,故:
,故:
原式 .
.
例5 试确定常数 与
与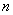 ,使得当
,使得当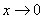 时,
时, 与
与 为等价无穷小.
为等价无穷小.
解  而左边
而左边 ,
,
故 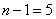 即
即
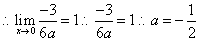 .
.
5.利用洛比达法则求极限
利用这一法则的前提是:函数的导数要存在;为0比0型或者 型等未定式类型.
型等未定式类型.
洛必达法则分为3种情况:(1)0比0,无穷比无穷的时候直接用.(2)0乘以无穷,无穷减去无穷(无穷大与无穷小成倒数关系时)通常无穷大都写成无穷小的倒数形式,通项之后,就能变成(1)中形式了.(3)0的0次方,1的无穷次方,无穷的0次方,对于(指数,幂函数)形式的方法主要是取指数的方法,这样就能把幂函数指数位置的函数移下来了,就是写成0与无穷的形式了.
洛必达法则中还有一个定理:当 时,函数
时,函数 及
及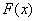 都趋于0;在点
都趋于0;在点 的某去心邻域内,
的某去心邻域内, ﹑
﹑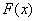 的导数都存在且
的导数都存在且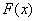 的导数不等于0;
的导数不等于0;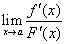 存在,那么
存在,那么 . [1]
. [1]
求极限有很多种方法如洛必达法则,夹逼定理求极限的秘诀是:强行代入,先定型后定法. [3]
例12  (例4)
(例4)
解:原式= 。(最后一步用到了重要极限)
。(最后一步用到了重要极限)
例13 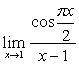
解:原式= 。
。
例14 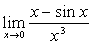
解:原式= =
= 。(连续用洛比达法则,最后用重要极限)
。(连续用洛比达法则,最后用重要极限)
例15 
解:
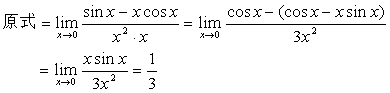
例18 
解:错误解法:原式= 。
。
正确解法:

应该注意,洛比达法则并不是总可以用,如下例。
例19 
解:易见:该极限是“ ”型,但用洛比达法则后得到:
”型,但用洛比达法则后得到: ,此极限
,此极限
不存在,而原来极限却是存在的。正确做法如下:
原式=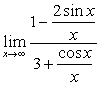 (分子、分母同时除以x)
(分子、分母同时除以x)
=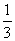 (利用定理1和定理2)
(利用定理1和定理2)
注:使用罗比达法则必须满足使用条件,要注意分母不能为零,导数存在。罗比达法则分为三种情况(1)0 比0 和无穷比无穷时候直接分子分母求导; (2) 0 乘以无穷,无穷减去无穷(应为无穷大于无穷小成倒数的关系)所以无穷大都 写成了无穷小的倒数形式了。 通项之后这样就能变成 1 的形式; (3) 的 0 次方, 0 1 的无穷次方,无穷的 0 次方,对于(指数幂数)方程,方法主要是取指数还取 对数的方法, 这
样就能把幂上的函数移下来了, 就是写成 0 与无穷的形式了, (这就是为什么只有 3 种形式的原因, )
6.利用极限存在准则求极限
例20 已知 ,求
,求
解:易证:数列 单调递增,且有界(0<
单调递增,且有界(0< <2),由准则1极限
<2),由准则1极限 存在,设
存在,设 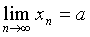 。对已知的递推公式
。对已知的递推公式 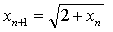 两边求极限,得:
两边求极限,得:
 ,解得:
,解得: 或
或 (不合题意,舍去)
(不合题意,舍去)
所以  。
。
例21 
解: 易见:
因为  ,
,
所以由准则2得: 。
。
7.直接使用求导的定义求极限
当题目中告诉你 时,
时,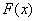 的导数等于0的时候,就是暗示你一定要用导数定义:
的导数等于0的时候,就是暗示你一定要用导数定义:
(1)设函数 在点
在点 的某个领域内有定义,当自变量
的某个领域内有定义,当自变量 在
在 处取得增量
处取得增量 (点
(点 仍在该领域内)时,相应的函数取得增量
仍在该领域内)时,相应的函数取得增量 ;如果
;如果 与
与 之比
之比 时的极限存在,则称函数
时的极限存在,则称函数 在点
在点 处可导,并称这个极限为函数
处可导,并称这个极限为函数 在点
在点 处可导,并称这个极限为函数
处可导,并称这个极限为函数 在点
在点 处的导数,记作
处的导数,记作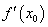 ,即
,即  ;
;
(2)在某点处可导的充分必要条件是左右导数都存在且相等.
例36 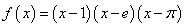 ,求
,求 .
.
解 
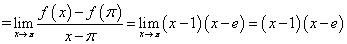 .
.
例37 若函数 有连续二阶导数且
有连续二阶导数且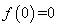 ,
,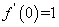 ,
, ,
,
则 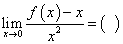 .
.
A:不存在 B:0 C:-1 D:-2
解 

 .
.
所以,答案为D.
例38 若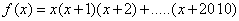 ,求
,求 .
.
解 


 .
.
8.求数列极限的时候可以将其转化为定积分[1]
例33 已知 ,在区间
,在区间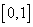 上求
上求 (其中将
(其中将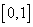 分为
分为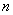 个小区间
个小区间 ,
,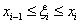 ,
,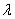 为
为 中的最大值).
中的最大值).
解 由已知得: 

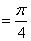 .
.
(注释:由已知可以清楚的知道,该极限的求解可以转化为定积分,求函数 在区间
在区间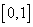 上的面积).
上的面积).
在有的极限的计算中,需要利用到如下的一些结论、概念和方法:
(1)定积分中值定理:如果函数 在积分区间
在积分区间 上连续,则在
上连续,则在 上至少有一个点,使下列公式成立:
上至少有一个点,使下列公式成立:

 ;
;
(2)设函数 在区间
在区间 上连续,取
上连续,取 ,如果极限
,如果极限  存在,则称此极限为函数
存在,则称此极限为函数 在无穷区间
在无穷区间 上的反常积分,记作
上的反常积分,记作 ,即
,即 ;
;
设 在区间
在区间 上连续且
上连续且 ,求以曲线
,求以曲线 为曲线,底为
为曲线,底为 的曲边梯形的面积
的曲边梯形的面积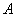 ,把这个面积
,把这个面积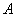 表示为定积分:
表示为定积分: 的步骤是:
的步骤是:
首先,用任意一组的点把区间 分成长度为
分成长度为 的
的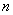 个小区间,相应地把曲线梯形分成
个小区间,相应地把曲线梯形分成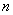 个窄曲边梯形,第
个窄曲边梯形,第 个窄曲边梯形的面积设为
个窄曲边梯形的面积设为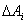 ,于是有
,于是有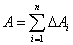 ;
;
其次,计算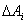 的近似值
的近似值  ;
;
然后,求和,得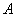 的近似值
的近似值  ;
;
最后,求极限,得 .
.
例34 设函数 连续,且
连续,且 ,求极限
,求极限 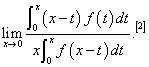 .
.
解  =
=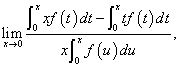
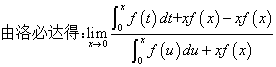 ,
,
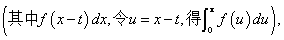

 .
.
例35 计算反常积分:  .
.
解  =
= =
= =
=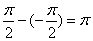 .
.
9.用初等方法变形后,再利用极限运算法则求极限
利用如下的极限运算法则来求极限:
(1)如果
那么

若又有 ,则
,则
(2)如果 存在,而
存在,而 为常数,则
为常数,则
(3)如果 存在,而
存在,而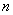 为正整数,则
为正整数,则
(4)如果 ,而
,而 ,则
,则
(5)设有数列 和
和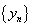 ,如果
,如果
那么,

当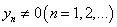 且
且 时,
时,
例1 
解:原式= 。
。
注:本题也可以用洛比达法则。
例2 
解:原式= 。
。
例3 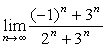
解:原式 。
。
三,极限运算思维的培养
极限运算考察的是一种基本能力,所以在做题或者看书的时候依赖的是基本概念和基本方法。掌握一定的技巧可以使学习事半功倍。而极限思维的培养则是对做题起到指导性的意义。如何培养,一方面要立足概念,另一方面则需要在具体的运算中体会,多做题多总结。
四. 结束语
上面对求极限的常用方法进行了比较全面的总结,由此可以看出,求极限方法灵活多样,而且许多题目不只用到一种方法,因此,要想熟练掌握各种方法,必须多做练习,在练习中体会。另外,求极限还有其它一些方法,如用定积分求极限等,由于平时练习中不经常使用,这里不作一一介绍了。
[参 考 文 献]
[1] 同济大学应用数学系 高等数学 1997
[2] 吉米多维奇.数学分析[M].济南:山东科技文献出版社1995.
[3] 陈纪修,等.数学分析[M].北京:高等教育出版社,1999.
[4] 同济大学应用数学组.高等数学[M].北京:高等教育出版社,1996.第3期张宏达:高等数学中求极限的常用方法
41? 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
《高等数学》极限运算技巧
《高等数学》的极限与连续是前几章的内容,对于刚入高校的学生而言是入门部分的重要环节。是“初等数学”向“高等数学”的起步阶段。
一,极限的概念
从概念上来讲的话,我们首先要掌握逼近的思想,所谓极限就是当函数的变量具有某种变化趋势(这种变化趋势是具有唯一性),那么函数的应变量同时具有一种趋势,而且这种趋势是与自变量的变化具有对应性。通俗的来讲,函数值因为函数变量的变化而无限逼近某一定值,我们就将这一定值称为该函数在变量产生这种变化时的极限!
从数学式子上来讲,逼近是指函数的变化,表示为。这个问题不再赘述,大家可以参考教科书上的介绍。
二,极限的运算技巧
我在上课时,为了让学生好好参照我的结论,我夸过这样一个海口,我说,只要你认真的记住这些内容,高数部分所要求的极限内容基本可以全部解决。现在想来这不是什么海口,数学再难也是基本的内容,基本的方法,关键是技巧性。我记得blog中我做过一道极限题,当时有网友惊呼说太讨巧了!其实不是讨巧,是有规律可循的!今天我写的内容希望可以对大家的学习有帮助!
我们看到一道数学题的时候,首先是审题,做极限题,首先是看它的基本形式,是属于什么形式采用什么方法。这基本上时可以直接套用的。
1,连续函数的极限
这个我不细说,两句话,首先看是不是连续函数,是连续函数的直接带入自变量。
2,不定型
我相信所有学习者都很清楚不定型的重要性,确实。那么下面详细说明一些注意点以及技巧。
第一,所有的含有无穷小的,首先要想到等价无穷小代换,因为这是最能简化运算的。等价代换的公式主要有六个: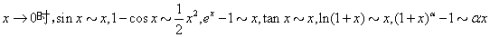
需要注意的是等价物穷小代换是有适用条件的,即:在含有加减运算的式子中不能直接代换,在部分式子的乘除因子也不能直接代换,那么如果一般方法解决不了问题的话,必须要等价代换的时候,必须拆项运算,不过,需要说明,拆项的时候要小心,必须要保证拆开的每一项极限都存在。
此外等价无穷小代换的使用,可以变通一些其他形式,比如: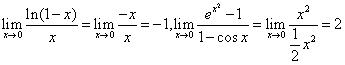 等等。特别强调在运算的之前,检验形式,是无穷小的形式才能等价代换。
等等。特别强调在运算的之前,检验形式,是无穷小的形式才能等价代换。
当然在一些无穷大的式子中也可以去转化代换,即无穷大的倒数是无穷小。这需要变通的看问题。
在无穷小的运算中,洛必答法则也是一种很重要的方法,但是洛必答法则适用条件比较单一,就是无穷小比无穷小。比较常见的采用洛必答法则的是无穷小乘无穷大的情况。(特别说明无穷小乘无穷大可以改写为无穷小比无穷小或者无穷大比无穷大的形式,这根据做题的需要来进行)。
第二,在含有∞的极限式中,一般可分为下面几种情况:
(1),“∞/∞ ”形式
如果是幂函数形式的(包含幂函数四则运算形式),可以找高次项,提出高次项,这样其他一切项就都是无穷小了,只有高次项是常数。比如: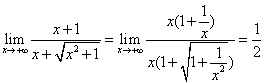 ,这道题中,可以看到提出最高次x(注意不是)其他项都是“0”,原来的x都是常数1了。当然如果分式形式中,只有分子中含有高次项,那么该极限式极限不存在(是无穷大),如果只有分母中含有高次项,那么该极限式极限为0,如果分子分母都含有高次项,我们可以直接去看高次项的系数,基本原理其实就是上面所说的提高次项。比如上面的例子,可以直接写1/2。
,这道题中,可以看到提出最高次x(注意不是)其他项都是“0”,原来的x都是常数1了。当然如果分式形式中,只有分子中含有高次项,那么该极限式极限不存在(是无穷大),如果只有分母中含有高次项,那么该极限式极限为0,如果分子分母都含有高次项,我们可以直接去看高次项的系数,基本原理其实就是上面所说的提高次项。比如上面的例子,可以直接写1/2。
如果不是纯幂函数形式,无法用提高次项的方法(提高次项是优先使用的方法),使用洛必达也是一种很好的方法。需要强调的是洛必达是一种解决“∞/∞ ”或“0/0 ”的基本方法,它的严格限制形式只有这两种,所以比较好观察。但是多数时候我们优先采用其他的方法来解决,这主要是考虑运算量的问题。
(2),“∞-∞ ”形式
“ ∞-∞”形式不能直接运算,需要转换形式,即转换成“∞/∞ ”或“0/0 ”的形式,基本解法同上。比如: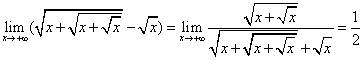
这道题是转换形式之后是“∞/∞ ”的形式,提高次项解。
(3)“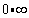 ”形式
”形式
这也是需要转换的一种基本形式。因为无穷大与无穷小之间的倒数关系,所以这种转换时比较简单也是比较容易解决的。转换之后的形式也是“∞/∞ ”或“0/0 ”的形式。
第三,“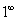 ”
”
这种形式的解决思路主要有两种。
第一种是极限公式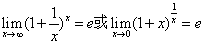 ,这种形式也是比较直观的。比如:
,这种形式也是比较直观的。比如: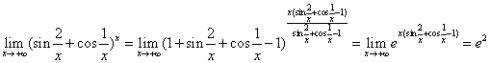 这道题的基本接替思路是,检验形式是“
这道题的基本接替思路是,检验形式是“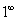 ”,然后选用公式,再凑出公式的形式,最后直接套用公式。
”,然后选用公式,再凑出公式的形式,最后直接套用公式。
第二种是取对数消指数。简单来说,“ 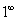 ”形式指数的存在是我们解题的主要困难。那么我们直接消掉指数就可以采用其他方法来解决了。比如上面那道题用取对数消指数的方法来解,是这样的:
”形式指数的存在是我们解题的主要困难。那么我们直接消掉指数就可以采用其他方法来解决了。比如上面那道题用取对数消指数的方法来解,是这样的: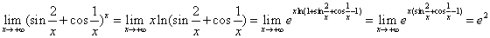
可以看出尽管思路切入点不一样,但是这两种方法有异曲同工之妙。
三,极限运算思维的培养
极限运算考察的是一种基本能力,所以在做题或者看书的时候依赖的是基本概念和基本方法。掌握一定的技巧可以使学习事半功倍。而极限思维的培养则是对做题起到指导性的意义。如何培养,一方面要立足概念,另一方面则需要在具体的运算中体会,多做题多总结。
-
高等数学求极限的常用方法(附例题和详解)
高等数学求极限的14种方法一、极限的定义1.极限的保号性很重要:设f(x)?A,注:它的使用有严格的使用前提。首先必须是X趋近,而…
-
高数中求极限的16种方法
高数中求极限的16种方法好东西假如高等数学是棵树木得话那么极限就是他的根函数就是他的皮树没有跟活不下去没有皮只能枯萎可见这一章的重…
-
高数求极限的16种方法(超经典)高彦辉总结
L.+'''+.+'''+.+天天快乐+'+..+'+.+爱爱爱爱祝爱爱愿爱爱你爱爱永爱爱远爱爱被爱爱爱爱爱包爱爱围爱爱爱爱爱爱爱…
-
高数 第1章 极限计算方法总结
极限计算方法总结一极限定义运算法则和一些结果1定义数列极限函数极限课本42页的表格必须认真填写并掌握说明1一些最简单的数列或函数的…
-
高等数学极限方法总结
极限摘要数列极限的求法一直是数列中一个比较重要的问题本文通过归纳和总结从不同的方面罗列了它的几种求法关键词高等数学数列极限定义洛比…
-
求极限方法小结
一.横向总结:1.活用2个重要极限2.a有界函数与无穷小的乘积是无穷小b无穷小与无穷大的关系:无穷大的倒数为无穷小,恒不为零的无穷…
-
高等数学求极限的常用方法(附例题和详解)
高等数学求极限的14种方法一、极限的定义1.极限的保号性很重要:设x?x0limf(x)?,(i)若A?0,则有??0,使得当0?…
-
高等数学B上册 求极限方法总结
求极限的几种常用方法1.约去零因子求极限例1:求极限limx?1x4?1x?1【说明】x?1表明x与1无限接近,但x?1,所以x?…
-
高数求极限的16种方法(超经典)高彦辉总结
L.+'''+.+'''+.+天天快乐+'+..+'+.+爱爱爱爱祝爱爱愿爱爱你爱爱永爱爱远爱爱被爱爱爱爱爱包爱爱围爱爱爱爱爱爱爱…
-
高数:总结求极限的常用方法
总结求极限的常用方法,详细列举,至少4种极限定义法泰勒展开法。洛必达法则。等价无穷小和等价无穷大。极限的求法1.直接代入法适用于分…
-
考研高数精华知识点总结:极限的性质
凯程考研历史悠久专注考研科学应试严格管理成就学员考研高数精华知识点总结极限的性质高等数学是考研数学考试中内容最多的一部分分值所占比…