《用数学归纳法证明不等式》参考教案
课题:用数学归纳法证明不等式
教学目标:
1、牢固掌握数学归纳法的证明步骤,熟练表达数学归纳法证明的过程。
2、通过事例,学生掌握运用数学归纳法,证明不等式的思想方法。
3、培养学生的逻辑思维能力,运算能力和分析问题,解决问题的能力。
重点、难点:
1、巩固对数学归纳法意义和有效性的理解,并能正确表达解题过程,以及掌握用数学归纳法证明不等式的基本思路。
2、应用数学归纳法证明的不同方法的选择和解题技巧。
教学过程:
一、复习导入:
1、上节课学习了数学归纳法及运用数学归纳法解题的步骤,请同学们回顾,说出数学归纳法的步骤?
(1)数学归纳法是用于证明某些与自然数有关的命题的一种方法。
(2)步骤:1)归纳奠基;
2)归纳递推。
2、作业讲评:(出示小黑板)
习题:用数学归纳法证明:2+4+6+8+……+2n=n(n+1)
如采用下面的证法,对吗?
证明:①当n=1时,左边=2=右边,则等式成立。
②假设n=k时,(k∈N,k≥1)等式成立,
即2+4+6+8+……+2k=k(k+1)
当n=k+1时,
2+4+6+8+……+2k+2(k+1)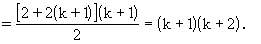
∴ n=k+1时,等式成立。
由①②可知,对于任意自然数n,原等式都成立。
(1)学生思考讨论。
(2)师生总结: 1)不正确
2)因为在证明n=k+1时,未用到归纳假设,直接用等差数列求和公式,违背了数学归纳法本质:递推性。
二、新知探究
明确了数学归纳法本质,我们共同讨论如何用数学归纳法证明不等式。
(出示小黑板)
例1 观察下面两个数列,从第几项起an始终小于bn?证明你的结论。
{an=n2}:1,4,9,16,25,36,49,64,81, ……
{bn=2n}:2,4,8,16,32,64,128,256,512, ……
(1)学生观察思考
(2)师生分析
(3)解:从第5项起,an < bn ,即 n²<2n,n∈N+(n≥5)
 证明:(1)当 n=5时,有52<25,命题成立。
证明:(1)当 n=5时,有52<25,命题成立。
(2)假设当n=k(k≥5)时命题成立
即k2<2k
当n=k+1时,因为
(k+1)2=k2+2k+1<k2+2k+k=k2+3k<k2+k2=2k2<2×2k=2k+1
所以,(k+1)2<2k+1
即n=k+1时,命题成立。
由(1)(2)可知n²<2n(n∈N+,n≥5)
学生思考、小组讨论:①放缩技巧:k2+2k+1<k2+2k+k;k2+3k<k2+k2
②归纳假设:2k2<2×2k
例2 证明不等式│Sin nθ│≤n│Sinθ│(n∈N+)
分析:这是一个涉及正整数n的三角函数问题,又与绝对值有关,在证明递推关系时,应注意利用三角函数的性质及绝对值不等式。
证明:(1)当 n=1时,上式左边=│Sinθ│=右边,不等式成立。
(2)假设当n=k(k≥1)时命题成立,
即有│Sin kθ│≤k│Sinθ│
当n=k+1时,
 │Sin (k+1)θ│=│Sin kθCosθ+Cos kθSin θ│
│Sin (k+1)θ│=│Sin kθCosθ+Cos kθSin θ│
≤│Sin kθCosθ│+│Cos kθSin θ│
=│Sin kθ││Cosθ│+│Cos kθ││Sin θ│
≤│Sin kθ│+│Sin θ│
≤k│Sinθ│+│Sin θ│
=(k+1)│Sinθ│
所以当n=k+1时,不等式也成立。
由(1)(2)可知,不等式对一切正整数n均成立。
学生思考、小组讨论:①绝对值不等式: │a+b│≤ │a│+│b│
②三角函数的有界性:│Sinθ│≤1,│Cosθ│≤1
③三角函数的两角和公式。
(板书)例3 证明贝努力(Bernoulli)不等式:
如果x是实数且x>-1,x≠0,n为大于1的自然数,那么有(1+x)n>1+nx
分析:①贝努力不等式中涉几个字母?(两个:x,n)
②哪个字母与自然数有关? (n是大于1的自然是数)
(板书)证:(1)当n=2时,左边=(1+x)2=1+2x+x2,右边=1+2x,因x2>0,则原不等式成立.
(在这里,一定要强调之所以左边>右边,关键在于x2>0是由已知条件x≠0获得,为下面证明做铺垫)
(2)假设n=k时(k≥2),不等式成立,即(1+x)k>1+kx.
师:现在要证的目标是(1+x)k+1>1+(k+1)x,请同学考虑.
生:因为应用数学归纳法,在证明n=k+1命题成立时,一定要运用归纳假设,所以当n=k+1时.应构造出归纳假设适应的条件.所以有:(1+x)k+1=(1+x)k(1+x),因为x>-1(已知),所以1+x>0于是(1+x)k(1+x)>(1+kx)(1+x).
师:现将命题转化成如何证明不等式
(1+kx)(1+x)≥1+(k+1)x.
显然,上式中“=”不成立.
故只需证:(1+kx)(1+x)>1+(k+1)x.
提问:证明不等式的基本方法有哪些?
生:证明不等式的基本方法有比较法、综合法、分析法.
(提问的目的是使学生明确在第二步证明中,合理运用归纳假设的同时,其本质是不等式证明,因此证明不等式的所有方法、技巧手段都适用)
生:证明不等式(1+kx)(1+x)>1+(k+1)x,可采用作差比较法.
(1+kx)(1+x)-[1+(k+1)x]
=1+x+kx+kx2-1-kx-x
=kx2>0(因x≠0,则x2>0).
所以,(1+kx)(1+x)>1+(k+1)x.
生:也可采用综合法的放缩技巧.
(1+kx)(1+x)=1+kx+x+lx2=1+(k+1)x+kx2.
因为kx2>0,所以1+(k+1)x+kx2>1+(k+1)x,即(1+kx)(1+x)>1+(1+k)x成立.
生:……
(学生可能还有其他多种证明方法,这样培养了学生思维品质的广阔性,教师应及时引导总结)
师:这些方法,哪种更简便,更适合数学归纳法的书写格式?学生用放缩技巧证明显然更简便,利于书写.
(板书)将例3的格式完整规范.
证明:(1)当n=2时,由x≠0得 (1+x)2=1+2x+x2>1+2x,不等式成立。
(2)假设n=k(k≥2)时,不等式成立,
即有(1+x)k>1+kx
当n=k+1时,
(1+x)k+1=(1+x)(1+x)k>(1+x)(1+kx)
=1+x+kx+ kx2>1+x+kx=1+(k+1)x
所以当n=k+1时,不等式成立
由①②可知,贝努力不等式成立。
(通过例题的讲解,在第二步证明过程中,通常要进行合理放缩,以达到转化目的)
三、课堂小结
1.用数学归纳法证明,要完成两个步骤,这两个步骤是缺一不可的.但从证题的难易来分析,证明第二步是难点和关键,要充分利用归纳假设,做好命题从n=k到n=k+1的转化,这个转化要求在变化过程中结构不变.
2.用数学归纳法证明不等式是较困难的课题,除运用证明不等式的几种基本方法外,经常使用的方法就是放缩法,针对目标,合理放缩,从而达到目标.
四、课后作业
1.课本P53:1,3,5
2.证明不等式:

第二篇:高中数学 第四讲《数学归纳法证明不等式》教案 新人教A版选修4-5
第四讲:数学归纳法证明不等式
数学归纳法证明不等式是高中选修的重点内容之一,包含数学归纳法的定义和数学归纳法证明基本步骤,用数学归纳法证明不等式。数学归纳法是高考考查的重点内容之一,在数列推理能力的考查中占有重要的地位。
本讲主要复习数学归纳法的定义、数学归纳法证明基本步骤、用数学归纳法证明不等式的方法:作差比较法、作商比较法、综合法、分析法和放缩法,以及类比与猜想、抽象与概括、从特殊到一般等数学思想方法。
在用数学归纳法证明不等式的具体过程中,要注意以下几点:
(1)在从n=k到n=k+1的过程中,应分析清楚不等式两端(一般是左端)项数的变化,也就是要认清不等式的结构特征;
(2)瞄准当n=k+1时的递推目标,有目的地进行放缩、分析;
(3)活用起点的位置;
(4)有的试题需要先作等价变换。
例题精讲
例1、用数学归纳法证明

分析:该命题意图:本题主要考查数学归纳法定义,证明基本步骤
证明:
1°当n=1时,左边=1- =
= ,右边=
,右边= =
= ,所以等式成立。
,所以等式成立。
2°假设当n=k时,等式成立,
即 。
。
那么,当n=k+1时,




这就是说,当n=k+1时等式也成立。
综上所述,等式对任何自然数n都成立。
点评:
数学归纳法是用于证明某些与自然数有关的命题的一种方法.设要证命题为P(n).(1)证明当n取第一个值n0时,结论正确,即验证P(n0)正确;(2)假设n=k(k∈N且k≥n0)时结论正确,证明当n=k+1时,结论也正确,即由P(k)正确推出P(k+1)正确,根据(1),(2),就可以判定命题P(n)对于从n0开始的所有自然数n都正确.
要证明的等式左边共2n项,而右边共n项。f(k)与f(k+1)相比较,左边增加两项,右边增加一项,并且二者右边的首项也不一样,因此在证明中采取了将 与
与 合并的变形方式,这是在分析了f(k)与f(k+1)的差异和联系之后找到的方法。
合并的变形方式,这是在分析了f(k)与f(k+1)的差异和联系之后找到的方法。
练习:
1.用数学归纳法证明3k≥n3(n≥3,n∈N)第一步应验证( )
A.n=1 B.n=2 C.n=3 D.n=4
解析:由题意知n≥3,∴应验证n=3.答案:C
2.用数学归纳法证明4 +3n+2能被13整除,其中n∈N
+3n+2能被13整除,其中n∈N
证明:
(1)当n=1时,42×1+1+31+2=91能被13整除
(2)假设当n=k时,42k+1+3k+2能被13整除,则当n=k+1时,
42(k+1)+1+3k+3=42k+1·42+3k+2·3-42k+1·3+42k+1·3
=42k+1·13+3·(42k+1+3k+2)
∵42k+1·13能被13整除,42k+1+3k+2能被13整除
∴当n=k+1时也成立.
由①②知,当n∈N*时,42n+1+3n+2能被13整除.
例2、求证: .
.
分析:该命题意图:本题主要考查应用数学归纳法证明不等式的方法和一般步骤。
用数学归纳法证明,要完成两个步骤,这两个步骤是缺一不可的.但从证题的难易来分析,证明第二步是难点和关键,要充分利用归纳假设,做好命题从n=k到n=k+1的转化,这个转化要求在变化过程中结构不变.
证明:
(1)当n=2时,右边= ,不等式成立.
,不等式成立.
(2)假设当 时命题成立,即
时命题成立,即
 .
.
则当 时,
时,

所以则当 时,不等式也成立.
时,不等式也成立.
由(1),(2)可知,原不等式对一切 均成立.
均成立.
点评:本题在由 到
到 时的推证过程中,
时的推证过程中,
(1)一定要注意分析清楚命题的结构特征,即由 到
到 时不等式左端项数的增减情况;
时不等式左端项数的增减情况;
(2)应用了放缩技巧:

例3、已知, ,
,
用数学归纳法证明: .
.
证明:
(1)当n=2时, ,∴命题成立.
,∴命题成立.
(2)假设当 时命题成立,即
时命题成立,即
 .
.
则当 时,
时,


所以则当 时,不等式也成立.
时,不等式也成立.
由(1),(2)可知,原不等式对一切 均成立.
均成立.
点评:本题在由 到
到 时的推证过程中,
时的推证过程中,
(1)不等式左端增加了 项,而不是只增加了“
项,而不是只增加了“ ”这一项,否则证题思路必然受阻;
”这一项,否则证题思路必然受阻;
(2)应用了放缩技巧:

练习:
1、证明不等式:

分析
1、数学归纳法的基本步骤:
设P(n)是关于自然数n的命题,若
1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.
2、用数学归纳法证明不等式是较困难的课题,除运用证明不等式的几种基本方法外,经常使用的方法就是放缩法,针对目标,合理放缩,从而达到目标.
证明:(1)当n=1时,不等式成立.
(2)假设n=k时,不等式成立,即

那么,


这就是说,n=k+1时,不等式也成立.
根据(1)(2)可知不等式对n∈N+都成立.
2.求证:用数学归纳法证明  .
.
证明:
(1) 当n=1时,  ,不等式成立;
,不等式成立;
当n=2时,  ,不等式成立;
,不等式成立;
当n=3时,  ,不等式成立.
,不等式成立.
(2)假设当 时不等式成立,即
时不等式成立,即  .
.
则当 时,
时,
 ,
,
∵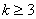 ,∴
,∴ ,(*)
,(*)
从而 ,
,
∴ .
.
即当 时,不等式也成立.
时,不等式也成立.
由(1),(2)可知, 对一切
对一切 都成立.
都成立.
点评: 因为在(*)处,当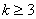 时才成立,故起点只证n=1还不够,因此我们需注意命题的递推关系式中起点位置的推移.
时才成立,故起点只证n=1还不够,因此我们需注意命题的递推关系式中起点位置的推移.
3.求证: ,其中
,其中 ,且
,且 .
.
分析:此题是20##年广东高考数学试卷第21题的适当变形,有两种证法
证法一:用数学归纳法证明.
(1)当m=2时, ,不等式成立.
,不等式成立.
(2)假设 时,有
时,有 ,
,
则  ,
,
∵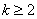 ,∴
,∴ ,即
,即 .
.
从而 ,
,
即 时,亦有
时,亦有 .
.
由(1)和(2)知,对 都成立.
都成立.
证法二:作差、放缩,然后利用二项展开式和放缩法证明.

∴当 ,且
,且 时,
时, .
.
例4、(20##年江西省高考理科数学第21题第(1)小题,本小题满分12分)
已知数列


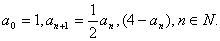
证明
求数列 的通项公式an.
的通项公式an.
分析:近年来高考对于数学归纳法的考查,加强了数列推理能力的考查。对数列进行了考查,和数学归纳法一起,成为压轴题。
解:(1)方法一 用数学归纳法证明:
1°当n=1时, ∴
∴ ,命题正确.
,命题正确.
2°假设n=k时有
则

而
又
∴ 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时, ∴
∴ ;
;
2°假设n=k时有 成立,
成立,
令 ,
, 在[0,2]上单调递增,
在[0,2]上单调递增,
所以由假设有:
即
也即当n=k+1时  成立,
成立,
所以对一切 .
.
(2)下面来求数列的通项:
所以 
 则
则

又bn=-1,所以
 .
.
点评:
本题问给出的两种方法均是用数学归纳法证明,所不同的是:方法一采用了作差比较法;方法二利用了函数的单调性.
本题也可先求出第(2)问,即数列 的通项公式
的通项公式 ,然后利用函数
,然后利用函数 的单调性和有界性,来证明第(1)问的不等式.但若这样做,则无形当中加大了第(1)问的难度,显然不如用数学归纳法证明来得简捷.
的单调性和有界性,来证明第(1)问的不等式.但若这样做,则无形当中加大了第(1)问的难度,显然不如用数学归纳法证明来得简捷.
练习:
1.试证明:不论正数a、b、c是等差数列还是等比数列,当n>1,n∈N*且a、b、c互不相等时,均有:an+cn>2bn.
分析:该命题意图:本题主要考查数学归纳法证明不等式,考查的知识包括等差数列、等比数列的性质及数学归纳法证明不等式的一般步骤.
技巧与方法:本题中使用到结论:(ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak·c+ck·a.
证明:(1)设a、b、c为等比数列,a= ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)
∴an+cn= +bnqn=bn(
+bnqn=bn( +qn)>2bn
+qn)>2bn
(2)设a、b、c为等差数列,则2b=a+c猜想 >(
>( )n(n≥2且n∈N*)
)n(n≥2且n∈N*)
下面用数学归纳法证明:
①当n=2时,由2(a2+c2)>(a+c)2,∴
②设n=k时成立,即
则当n=k+1时, (ak+1+ck+1+ak+1+ck+1)
(ak+1+ck+1+ak+1+ck+1)
> (ak+1+ck+1+ak·c+ck·a)=
(ak+1+ck+1+ak·c+ck·a)= (ak+ck)(a+c)
(ak+ck)(a+c)
>( )k·(
)k·( )=(
)=( )k+1
)k+1
根据①、②可知不等式对n>1,n∈N*都成立.
二.基础训练
一、选择题
1.已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n),则最大的m的值为( )
A.30 B.26 C.36 D.6
解析:∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
证明:n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1-(2k+7)·3k
=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2(k≥2)
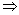 f(k+1)能被36整除
f(k+1)能被36整除
∵f(1)不能被大于36的数整除,∴所求最大的m值等于36.
答案:C
二、填空题
2.观察下列式子: …则可归纳出_________.
…则可归纳出_________.
解析:

 (n∈N*)
(n∈N*)
 (n∈N*)
(n∈N*)
3.已知a1= ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.
,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.

 、
、 、
、 、
、

三、解答题
4.若n为大于1的自然数,求证: .
.
证明:(1)当n=2时,
(2)假设当n=k时成立,即

所以:对于n∈N*,且n>1时,有
5.已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+ )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与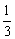 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
(1)解:设数列{bn}的公差为d,由题意得 ,∴bn=3n-2
,∴bn=3n-2
(2)证明:由bn=3n-2知
Sn=loga(1+1)+loga(1+ )+…+loga(1+
)+…+loga(1+ )
)
=loga[(1+1)(1+ )…(1+
)…(1+  )]
)]
而 logabn+1=loga
logabn+1=loga ,于是,比较Sn与
,于是,比较Sn与 logabn+1的大小
logabn+1的大小 比较(1+1)(1+
比较(1+1)(1+ )…(1+
)…(1+ )与
)与 的大小.
的大小.
取n=1,有(1+1)=
取n=2,有(1+1)(1+
推测:(1+1)(1+ )…(1+
)…(1+ )>
)> (*)
(*)
①当n=1时,已验证(*)式成立.
②假设n=k(k≥1)时(*)式成立,即(1+1)(1+ )…(1+
)…(1+ )>
)>
则当n=k+1时,


 ,即当n=k+1时,(*)式成立
,即当n=k+1时,(*)式成立
由①②知,(*)式对任意正整数n都成立.
于是,当a>1时,Sn> logabn+1,当 0<a<1时,Sn<
logabn+1,当 0<a<1时,Sn< logabn+1
logabn+1
6.设实数q满足|q|<1,数列{an}满足:a1=2,a2≠0,an·an+1=-qn,求an表达式,又如果 S2n<3,求q的取值范围.
S2n<3,求q的取值范围.
解:∵a1·a2=-q,a1=2,a2≠0,
∴q≠0,a2=- ,
,
∵an·an+1=-qn,an+1·an+2=-qn+1
两式相除,得 ,即an+2=q·an
,即an+2=q·an
于是,a1=2,a3=2·q,a5=2·qn…猜想:a2n+1=- qn(n=1,2,3,…)
qn(n=1,2,3,…)
综合①②,猜想通项公式为an=
下证:(1)当n=1,2时猜想成立
(2)设n=2k-1时,a2k-1=2·qk-1则n=2k+1时,由于a2k+1=q·a2k-1
∴a2k+1=2·qk即n=2k-1成立.
可推知n=2k+1也成立.
设n=2k时,a2k=- qk,则n=2k+2时,由于a2k+2=q·a2k,
qk,则n=2k+2时,由于a2k+2=q·a2k,
所以a2k+2=- qk+1,这说明n=2k成立,可推知n=2k+2也成立.
qk+1,这说明n=2k成立,可推知n=2k+2也成立.
综上所述,对一切自然数n,猜想都成立.
这样所求通项公式为an=
S2n=(a1+a3…+a2n-1)+(a2+a4+…+a2n)
=2(1+q+q2+…+qn-1)- (q+q2+…+qn)
(q+q2+…+qn)

由于|q|<1,∴ =
=
依题意知 <3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
<3,并注意1-q>0,|q|<1解得-1<q<0或0<q<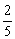
三.巩固练习
1. (06 年湖南卷. 理 .19本小题满分14分)
已知函数 ,数列{
,数列{ }满足:
}满足:
证明:(ⅰ) ;(ⅱ)
;(ⅱ) .
.
证明: (I).先用数学归纳法证明 ,n=1,2,3,…
,n=1,2,3,…
(i).当n=1时,由已知显然结论成立.
(ii).假设当n=k时结论成立,即 .因为0<x<1时
.因为0<x<1时
 ,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
从而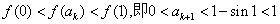 .故n=k+1时,结论成立.
.故n=k+1时,结论成立.
由(i)、(ii)可知, 对一切正整数都成立.
对一切正整数都成立.
又因为 时,
时, ,
,
所以 ,综上所述
,综上所述 .
.
(II).设函数 ,
, .由(I)知,当
.由(I)知,当 时,
时,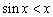 ,
,
从而
所以g (x)在(0,1)上是增函数. 又g (x)在[0,1]上连续,且g (0)=0,
所以当 时,g (x)>0成立.于是
时,g (x)>0成立.于是 .
.
故 .
.
点评:不等式的问题常与函数、三角、数列、导数、几何等数学分支交汇,综合考查运用不等式知识解决
问题的能力,在交汇中尤其以各分支中蕴藏的不等式结论的证明为重点. 需要灵活运用各分支的数学知识.
2. ( 05 年辽宁卷.19本小题满分12分)
已知函数 设数列
设数列 }满足
}满足 ,数列
,数列 }满足
}满足
(Ⅰ)用数学归纳法证明 ;
;
(Ⅱ)证明
分析:本小题主要考查数列、等比数列、不等式等基本知识,考查运用数学归纳法解决有关问题的能力
(Ⅰ)证明:当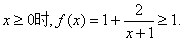 因为a1=1,
因为a1=1,
所以
下面用数学归纳法证明不等式
(1)当n=1时,b1= ,不等式成立,
,不等式成立,
(2)假设当n=k时,不等式成立,即
那么 

所以,当n=k+1时,不等也成立。
根据(1)和(2),可知不等式对任意n∈N*都成立。
(Ⅱ)证明:由(Ⅰ)知, 
所以 


故对任意 )
)
3.(05 年湖北卷.理22.本小题满分14分)
已知不等式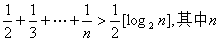 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过 的最大整数. 设数列
的最大整数. 设数列 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明
(Ⅱ)猜测数列 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
分析:本小题主要考查数列、极限及不等式的综合应用以及归纳递推的思想.
(Ⅰ)证法1:∵当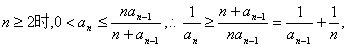
即
于是有 
所有不等式两边相加可得 
由已知不等式知,当n≥3时有,
∵
证法2:设 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式

(i)当n=3时, 由 
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即
则

即当n=k+1时,不等式也成立.
由(i)、(ii)知,
又由已知不等式得 
(Ⅱ)有极限,且
(Ⅲ)∵
则有
故取N=1024,可使当n>N时,都有
-
范例教学法教学设计
范例教学法教学设计课题名称卫生值日表教学目标1知识与技能学会制作空表格能按要求美化表格设置单元格字体颜色背景颜色合并单元格对齐单元…
-
运用范例教学法的教学设计
初中语文问题教学法的教学设计春教学案例第一环节提出问题一明确目标1积累生字词能正确流利有感情地朗读课文2理清写作思路理解文中描绘的…
- 运用范例教学法的教学设计---组合图形的面积
-
范例教学法
范例教学法范例教学法是德国的教育家瓦根舍因所创立的一种教育方法这种教育方法是为了解决知识的量的急剧膨胀与人的悠闲地学习时间学习能力…
-
范例教学法教学设计
范例教学法教学设计课题名称卫生值日表教学目标1知识与技能学会制作空表格能按要求美化表格设置单元格字体颜色背景颜色合并单元格对齐单元…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…