圆锥曲线总结
圆锥曲线与方程
课 题:小结与复习
教学目的:
1. 椭圆的定义、标准方程、焦点、焦距,椭圆的几何性质,椭圆的画法; 双曲线的定义、标准方程、焦点、焦距,双曲线的几何性质,双曲线的画法,等轴双曲线;抛物线的定义、标准方程、焦点、焦距,抛物线的几何性质,抛物线的画法,
2. 结合教学内容对学生进行运动变化和对立统一的观点的教育
教学重点:椭圆、双曲线、抛物线的定义、方程和几何性质;坐标法的应用.
教学难点:椭圆、双曲线的标准方程的推导过程;利用定义、方程和几何性质求有关焦点、焦距、准线等.
授课类型:复习课
课时安排:1课时
教 具:多媒体、实物投影仪
教学过程:
一、课前预习
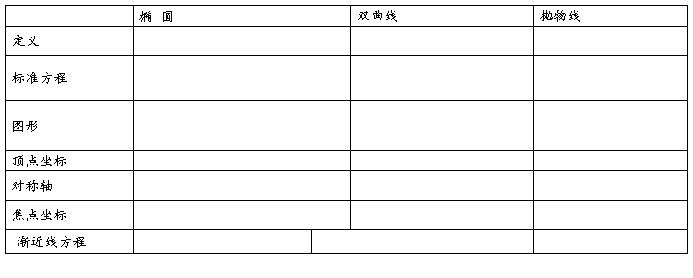
二、复习引入:
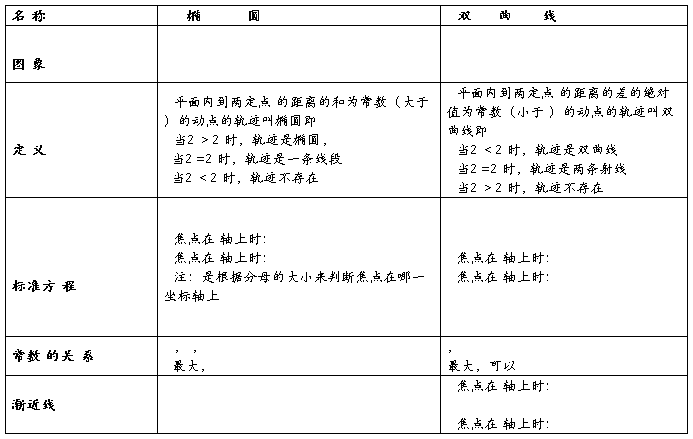
抛物线:

三、章节知识点回顾:
椭圆、双曲线、抛物线分别是满足某些条件的点的轨迹,由这些条件可以求出它们的标准方程,并通过分析标准方程研究这三种曲线的几何性质
1.椭圆定义:在平面内,到两定点距离之和等于定长(定长大于两定点间的距离)的动点的轨迹
2.椭圆的标准方程:, ()
3.椭圆的性质:由椭圆方程()
(1)范围: ,,椭圆落在组成的矩形中.
(2)对称性:图象关于轴对称.图象关于轴对称.图象关于原点对称原点叫椭圆的对称中心,简称中心.轴、轴叫椭圆的对称轴.从椭圆的方程中直接可以看出它的范围,对称的截距
(3)顶点:椭圆和对称轴的交点叫做椭圆的顶点
椭圆共有四个顶点: ,加两焦点共有六个特殊点叫椭圆的长轴,叫椭圆的短轴.长分别为 分别为椭圆的长半轴长和短半轴长椭圆的顶点即为椭圆与对称轴的交点
(4)离心率: 椭圆焦距与长轴长之比
椭圆形状与的关系:,椭圆变圆,直至成为极限位置圆,此时也可认为圆为椭圆在时的特例椭圆变扁,直至成为极限位置线段,此时也可认为圆为椭圆在时的特例
4.双曲线的定义:平面内到两定点的距离的差的绝对值为常数(小于)的动点的轨迹叫双曲线 即 这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距
在同样的差下,两定点间距离较长,则所画出的双曲线的开口较开阔(两条平行线)两定点间距离较短(大于定差),则所画出的双曲线的开口较狭窄(两条射线)双曲线的形状与两定点间距离、定差有关
5.双曲线的标准方程及特点:
(1)双曲线的标准方程有焦点在x轴上和焦点y轴上两种:
焦点在轴上时双曲线的标准方程为:(,);
焦点在轴上时双曲线的标准方程为:(,)
6.有关系式成立,且
其中a与b的大小关系:可以为
7焦点的位置:从椭圆的标准方程不难看出椭圆的焦点位置可由方程中含字母、项的分母的大小来确定,分母大的项对应的字母所在的轴就是焦点所在的轴而双曲线是根据项的正负来判断焦点所在的位置,即项的系数是正的,那么焦点在轴上;项的系数是正的,那么焦点在轴上
8.双曲线的几何性质:
(1)范围、对称性
由标准方程,从横的方向来看,直线x=-a,x=a之间没有图象,从纵的方向来看,随着x的增大,y的绝对值也无限增大,所以曲线在纵方向上可无限伸展,不像椭圆那样是封闭曲线双曲线不封闭,但仍称其对称中心为双曲线的中心
(2)顶点
顶点:,特殊点:
实轴:长为2a, a叫做半实轴长虚轴:长为2b,b叫做虚半轴长
双曲线只有两个顶点,而椭圆则有四个顶点,这是两者的又一差异
(3)渐近线
过双曲线的渐近线()
(4)离心率
双曲线的焦距与实轴长的比,叫做双曲线的离心率范围:
双曲线形状与e的关系:,e越大,即渐近线的斜率的绝对值就大,这是双曲线的形状就从扁狭逐渐变得开阔由此可知,双曲线的离心率越大,它的开口就越阔
9.等轴双曲线
定义:实轴和虚轴等长的双曲线叫做等轴双曲线,这样的双曲线叫做等轴双曲线 等轴双曲线的性质:(1)渐近线方程为:;(2)渐近线互相垂直;(3)离心率
10.共渐近线的双曲线系
如果已知一双曲线的渐近线方程为,那么此双曲线方程就一定是:或写成
11.共轭双曲线
以已知双曲线的实轴为虚轴,虚轴为实轴,这样得到的双曲线称为原双曲线的共轭双曲线 区别:三量a,b,c中a,b不同(互换)c相同共用一对渐近线 双曲线和它的共轭双曲线的焦点在同一圆上确定双曲线的共轭双曲线的方法:将1变为-1
12.双曲线的焦点弦:
定义:过焦点的直线割双曲线所成的相交弦
焦点弦公式:
当双曲线焦点在x轴上时,
过左焦点与左支交于两点时:
过右焦点与右支交于两点时:
当双曲线焦点在y轴上时,
过左焦点与左支交于两点时:
过右焦点与右支交于两点时:
13.双曲线的通径:
定义:过焦点且垂直于对称轴的相交弦
14 抛物线定义:
平面内与一个定点F和一条定直线的距离相等的点的轨迹叫做抛物线定点F叫做抛物线的焦点,定直线叫做抛物线的准线
15.抛物线的准线方程:
(1), 焦点:,准线:
(2), 焦点:,准线:
(3), 焦点:,准线:
(4) , 焦点:,准线:
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的,即
不同点:(1)图形关于X轴对称时,X为一次项,Y为二次项,方程右端为、左端为;图形关于Y轴对称时,X为二次项,Y为一次项,方程右端为,左端为 (2)开口方向在X轴(或Y轴)正向时,焦点在X轴(或Y轴)的正半轴上,方程右端取正号;开口在X轴(或Y轴)负向时,焦点在X轴(或Y轴)负半轴时,方程右端取负号
16.抛物线的几何性质
(1)范围
因为p>0,由方程可知,这条抛物线上的点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性
以-y代y,方程不变,所以这条抛物线关于x轴对称,我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程中,当y=0时,x=0,因此抛物线的顶点就是坐标原点.
(4)离心率
抛物线上的点M与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e表示.由抛物线的定义可知,e=1.
17抛物线的焦半径公式:
抛物线,
抛物线,
抛物线,
抛物线,
18.直线与抛物线:
(1)位置关系:
相交(两个公共点或一个公共点);相离(无公共点);相切(一个公共点)
将代入,消去y,得到
关于x的二次方程 (*)
若,相交;,相切;,相离
综上,得:
联立,得关于x的方程
当(二次项系数为零),唯一一个公共点(交点)
当,则
若,两个公共点(交点)
,一个公共点(切点)
,无公共点 (相离)
(2)相交弦长:
弦长公式:,
(3)焦点弦公式:
抛物线,
抛物线,
抛物线,
抛物线,
(4)通径:
定义:过焦点且垂直于对称轴的相交弦 通径:
(5)若已知过焦点的直线倾斜角
则
(6)常用结论:
和
和
四、【例题】
1.动点A到定点F1(0, -2)和F2(0, 2)的距离的和为4,则动点A的轨迹为 ( B )
A. 椭圆 B. 线段 C. 无图形 D. 两条射线;
2.动点P到定点F1(1, 0)的距离比它到定点F2(3, 0)的距离小2,则点P的轨迹是 ( C )
A.双曲线 B.双曲线的一支 C.一条射线 D.两条射线
3.人造地球卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为R,卫星近地点、远地点离地面的距离分别为 r1、r2 ,求卫星轨道的离心率.
4.两定点的坐标分别为A(-1, 0),B(2, 0),动点M满足∠MBA=2∠MAB,求动点M的轨迹方程.
五【课后作业】
六、板书设计(略)
七、课后记:
第二篇:线代总结
《线性代数及其应用》
一、行列式
1、余子式,代数余子式
2、行列式的展开定理(定理2.2,2.3,2.4)
按行展开: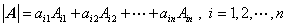
按列展开:
定理2.4 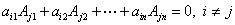 ;
;
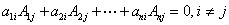 .
.
3、行列式的性质
(1) 拆性
(2) 若行列式有两行(列)成比例,则行列式等于零.
(3) 初等变换性质
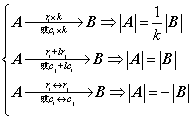
4、行列式计算:三角化法,降阶法(性质+展开定理),递推(归纳),范德蒙德、三对角
5、分块矩阵的行列式
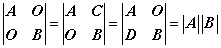
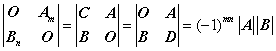
二、矩阵
1、矩阵及其运算(加法、数乘、乘法、幂、转置、方阵的行列式、分块运算)
(1) 乘法的结合律
(2) 方阵的幂的求解
(3) 转置的性质: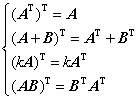
(4) 方阵的行列式:
(5) 分块运算(转置、乘法--例3.13、3.14)
2、初等变换及初等矩阵
左行右列

3、可逆矩阵
(1) 定义、性质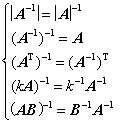
(2) 伴随矩阵 
(3) 判定: 可逆
可逆
(4) 逆矩阵的求法 
(5) 分块矩阵的逆
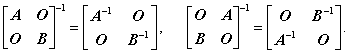
(6) 矩阵方程的求解: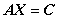 ,其中
,其中 可逆.
可逆.
法1 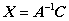 .
.
法2  .
.
4、矩阵的秩与矩阵的相抵
(1) 矩阵的秩与性质(101页,105-107页)
① 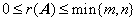 ;
;
② 子矩阵的秩不会超过原矩阵的秩;
③ 
④ 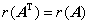 ;
;
⑤ 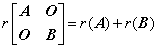 ;
;
⑥ 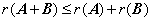 ;
;
⑦ 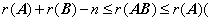 或
或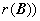 ;
;
若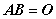 ,则
,则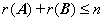 ,其中
,其中 ,
,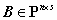 .
.
⑧ 设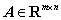 ,则
,则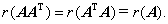
(2) 求矩阵的秩 (理论依据:矩阵的初等变换不改变矩阵的秩)
 (行阶梯形矩阵),
(行阶梯形矩阵),
则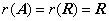 的非零行的个数.
的非零行的个数.
(3) 矩阵的相抵(等价)
① 
② 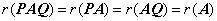 ,其中
,其中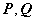 可逆.
可逆.
③ 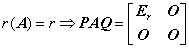 或
或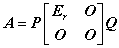 .
.
三、线性空间
1、概念、子空间的验证(非空、加法和数乘的封闭)
2、向量组的线性相关性的判断(命题4.2、4.3、4.4、4.5、定理4.1、4.2、4.4)
(1) 证明方法--定义、秩、坐标化
(2) 充要: 线性相关
线性相关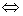 其中至少有一个向量可由其余向量线性表示.
其中至少有一个向量可由其余向量线性表示.
充分: 线性相关
线性相关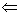 部分向量组线性相关
部分向量组线性相关
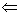 向量的个数
向量的个数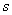 大于向量分量的个数
大于向量分量的个数
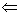
 被个数少于
被个数少于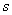 的向量组线性表示
的向量组线性表示
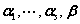 线性无关
线性无关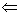

3、等价向量组
(1) (Ⅰ)可由(Ⅱ)线性表示,则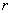 (Ⅰ)
(Ⅰ) 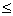
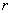 (Ⅱ).
(Ⅱ).
(2) (Ⅰ)与(Ⅱ)等价,则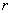 (Ⅰ)
(Ⅰ) 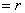 (Ⅱ).
(Ⅱ).
4、向量组的秩及极大无关组(命题4.6)、线性空间的基与维数
(1) 写成列向量作初等行变换.
(2) 对于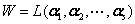 ,则
,则 , 即生成子空间的维数
, 即生成子空间的维数
与基就是向量组 的秩与极大无关组.
的秩与极大无关组.
5、坐标的概念、基变换公式与坐标变换公式
基变换公式: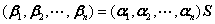
坐标变换公式:
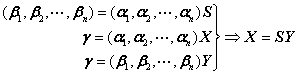 或
或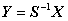
四、线性方程组(含参量、不含参量)
1、解的情况
(1) 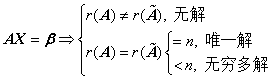
若 是方阵,则
是方阵,则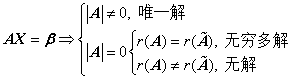
(2) 齐次线性方程组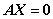 有非零解
有非零解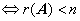 .
.
若 是方阵,则齐次线性方程组
是方阵,则齐次线性方程组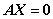 有非零解
有非零解 .
.
2、解的结构
齐次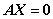 :
:
(1) 解空间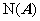 、
、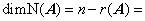 基础解系所含向量的个数
基础解系所含向量的个数
(2) 结构式:通解=基础解系的线性组合
非齐次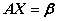 :
:
(1) 非-非=齐
(2) 结构式:通解=特解 导出组
导出组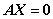 的基础解系的线性组合
的基础解系的线性组合
五、线性变换
1、线性变换的验证 (定义5.4)
2、线性变换在一个基下的矩阵(定义5.7)、命题5.8

3、线性变换在不同基下的矩阵之间的关系(相似) 定理5.9
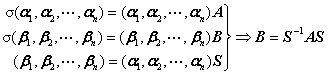
六、内积空间
1、内积的概念、长度、正交(正交向量组必线性无关)
2、施密特正交化
3、正交矩阵(定义、性质)
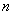 阶实矩阵
阶实矩阵 是正交矩阵的充要条件是
是正交矩阵的充要条件是 的列(行)向量组是
的列(行)向量组是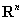 的一个标准正交基.
的一个标准正交基.
七、矩阵的相似对角形
1、特征值和特征向量的定义、性质
2、相似矩阵的定义、性质(迹、秩、行列式、特征值相等)
相似的判定:若 与
与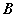 可对角化,且
可对角化,且 与
与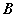 具有相同的特征值,则
具有相同的特征值,则 与
与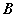 相似.
相似.
3、矩阵的相似对角化
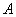 可对角化
可对角化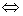
 有
有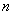 个线性无关的特征向量
个线性无关的特征向量
 数域
数域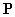 内有
内有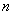 个特征值,每一个特征值的几何重数等于代数重数
个特征值,每一个特征值的几何重数等于代数重数
(充分条件)  有
有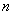 个互不相同的特征值
个互不相同的特征值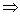
 可对角化
可对角化
4、实对称矩阵
(1) 特征值:实对称矩阵有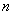 个实特征值.
个实特征值.
(2) 特征向量:实对称矩阵的属于不同特征值的特征向量正交.
(3) 实对称矩阵必正交相似于对角矩阵(几何重数等于代数重数).
(4)  与
与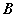 均为实对称矩阵,则
均为实对称矩阵,则 与
与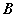 正交相似
正交相似
 与
与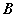 具有相同的特征值.
具有相同的特征值.
(正交相似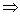 相似、合同)
相似、合同)
八、二次型
1、二次型的矩阵及秩
2、矩阵的合同:合同必相抵;正交相似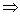 相似、合同
相似、合同
实对称矩阵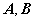 合同
合同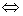
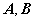 的正惯性指数与秩相同
的正惯性指数与秩相同
3、化二次型为标准形(不唯一)--正交替换法、配方法
4、惯性定理:实二次型的规范形唯一
5、正定二次型
(1) 判定:① 定义;
②  的特征值都大于零(
的特征值都大于零( 的正惯性指数等于
的正惯性指数等于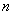 );
);
③  与
与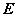 合同(与正定矩阵
合同(与正定矩阵 合同的实对称矩阵
合同的实对称矩阵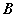 正定);
正定);
④ 存在可逆矩阵 ,使得
,使得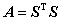 ;
;
⑤  的所有顺序主子式都大于零
的所有顺序主子式都大于零
(2) 必要条件: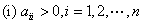 ;
;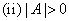
-
高中数学圆锥曲线总结
数学圆锥曲线总结1、圆锥曲线的两个定义:(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F,F的距离的和等于常数,且…
-
圆锥曲线总结相当好
圆锥曲线应用一、圆锥曲线的最值问题方法1:定义转化法x2y2例1、已知点F是双曲线4-12=1的左焦点,定点A的坐标为(1,4),…
-
圆锥曲线总结
圆锥曲线的概念与性质一、椭圆中的结论?x?acos?x2y21.椭圆2?2?1(a?b?0)的参数方程为?(?是参数)y?bsin…
-
圆锥曲线总结
圆锥曲线与方程课题小结与复习教学目的1椭圆的定义标准方程焦点焦距椭圆的几何性质椭圆的画法双曲线的定义标准方程焦点焦距双曲线的几何性…
-
圆锥曲线的经典性质总结
椭圆必背的经典结论1点P处的切线PT平分PF1F2在点P处的外角2PT平分PF1F2在点P处的外角则焦点在直线PT上的射影H点的轨…
-
圆锥曲线知识点总结(绝对物超所值)
圆锥曲线的方程与性质1.椭圆(1)椭圆概念平面内与两个定点F1、F2的距离的和等于常数2a(大于|F1F2|)的点的轨迹叫做椭圆。…
-
高中数学圆锥曲线总结
数学圆锥曲线总结1、圆锥曲线的两个定义:(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F,F的距离的和等于常数,且…
-
高考数学复习知识点总结——圆锥曲线
高中数学圆锥曲线方程§08.圆锥曲线方程知识要点一、椭圆方程.1.椭圆方程的第一定义:PF1?PF2?2a?F1F2方程为椭圆,P…
-
圆锥曲线知识点总结
高中数学圆锥曲线选知识点总结一、椭圆1、定义:平面内与两个定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹称为椭圆.即:…
-
高中数学圆锥曲线解题技巧方法总结[1]
圆锥曲线1.圆锥曲线的两定义:第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F1,F2的距离的和等于常数2a,且此常数2…
-
圆锥曲线基础知识汇总表
常用经验公式1.圆的切线方程(1)已知圆x2?y2?Dx?Ey?F?0.①若已知切点(x0,y0)在圆上,则切线只有一条,其方程是…