线代总结
20xx年X1 特征值,特征向量,线性无关
X2 伴随矩阵,初等变换(初等矩阵)
T1 矩阵行列式,运用矩阵乘法公式 B=AX,则{B}={A}{X}
F1(1)已知二次型的秩,求参数A。
(2)运用正交变换,化为标准形(求特征值,特征向量,构造正交矩阵)
(3)求方程的解(可用配方法)
F2 已知AB=O,讨论AX=O的通解(r(A)+r(B)≤n,B的列向量
为AX=O的通解)。
20xx年X1 线性无关 线性相关
X2 矩阵变换的初等矩阵表示(左行右列),矩阵的等价性
T1 矩阵的行列式BA=B+2E,已知A,求B
F1 (1) 线性方程组系数中含有参数,验证秩为2.
(2)求解参数以及方程组的解。
F2 实对称矩阵,求解特征值,特征向量。构造正交矩阵Q进行对角化。
20xx年X1 已知线性无关,验证线性相关。
X2 合同,相似的条件。(实对称矩阵A和B相似,则A和B合同)
T1 已知A,求A的三次方构成的矩阵的秩。
F1 已知两个方程组有公共解,求参数a和所有公共解。
F2 已知A的特征值,B为A的函数,求B的特征值,并求B的特征向量和矩阵B
本身。(A为实对称矩阵,则B也为实对称矩阵。实对称矩阵不同特征值的特征向量相互正
交)。
20xx年X1 判断矩阵E+A(E-A)的可逆性
X2 利用图形推出二次型的标准形式,判断正特征值的个数。
T1 求解特征值
F1 判断秩的大小,运用线性相关进一步讨论秩的大小。
F2(1)运用数学归纳法(迭代形式),讨论n阶矩阵的行列式
(2)方程组有唯一解,判断参数,并求解X1.(克拉莫法则)
(3)方程组有无穷多解,判断参数,并求通解(注意解的结构)
20xx年X1 两组机之间的过渡矩阵A=BX
X2 讨论分块矩阵(副对角线)的伴随矩阵
T1 求解特征值
F1 (1)求解非齐次线性方程组的通解
(2)判断三个三维向量的线性无关性
F2 (1)二次型中带有参数,求所有的特征值
(2)已知规范形(即正负惯性指数),确定参数A。
20xx年X1 考察矩阵的秩
X2求解A的相似矩阵(利用实对称矩阵A的特征值)
T1 利用向量空间的维数确定向量中的参数
F1 (1)已知方程解的个数,求解系数矩阵中的参数
( 2 )求解非齐次线性方程组AX=b的通解
F2 (1)已知A的特征值和特征向量,反求矩阵A。
(2)验证A+ E的正定性(利用特征值)
20xx年X1 考察初等变换的矩阵表示形式
X2 考察矩阵A和伴随矩阵之间秩的关系,进而讨论基础解系。
T1 已知标准型(即特征值),利用矩阵特征值和行列式之间的关系,反求矩阵中的参数。
F1(1)已知向量组A不能由向量组B线性表示,反求参数
(2)求解两个向量组A和B的线性表示。
F2 (1)求解实对称矩阵A的特征值和特征向量
(2 )利用特征值和特征向量,反求矩阵A。
20xx年X1 考察三个三维向量的线性相关性
X2 考察矩阵的相似性
T1 求解矩阵A-B的秩(利用相似性)
F1(1)计算四阶矩阵的行列式(带有参数A)
(2)非齐次线性方程组无穷多解,反求参数,并求通解
F2 (1)已知二次型的秩,反求参数A
(2)求正交变换,化为标准形。
20xx年X1已知矩阵方程AB=C,考察向量组的等价性
X2两矩阵相似的充要条件
T1已知代数余子式及其关系,求矩阵A的行列式
F1矩阵方程AC-CA=B,确定A,B矩阵中的参数,并求矩阵C。
F2 (1) 求二次型的矩阵(对称)表示形式
(2)验证二次型在正交变换下的标准形(运用特征值)。
第二篇:线代总结
《线性代数及其应用》
一、行列式
1、余子式,代数余子式
2、行列式的展开定理(定理2.2,2.3,2.4)
按行展开: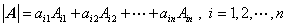
按列展开:
定理2.4 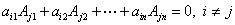 ;
;
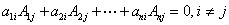 .
.
3、行列式的性质
(1) 拆性
(2) 若行列式有两行(列)成比例,则行列式等于零.
(3) 初等变换性质
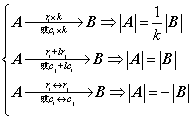
4、行列式计算:三角化法,降阶法(性质+展开定理),递推(归纳),范德蒙德、三对角
5、分块矩阵的行列式
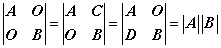
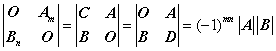
二、矩阵
1、矩阵及其运算(加法、数乘、乘法、幂、转置、方阵的行列式、分块运算)
(1) 乘法的结合律
(2) 方阵的幂的求解
(3) 转置的性质: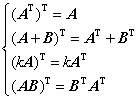
(4) 方阵的行列式:
(5) 分块运算(转置、乘法--例3.13、3.14)
2、初等变换及初等矩阵
左行右列

3、可逆矩阵
(1) 定义、性质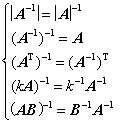
(2) 伴随矩阵 
(3) 判定: 可逆
可逆
(4) 逆矩阵的求法 
(5) 分块矩阵的逆
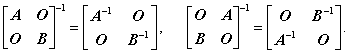
(6) 矩阵方程的求解: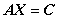 ,其中
,其中 可逆.
可逆.
法1 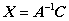 .
.
法2  .
.
4、矩阵的秩与矩阵的相抵
(1) 矩阵的秩与性质(101页,105-107页)
① 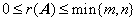 ;
;
② 子矩阵的秩不会超过原矩阵的秩;
③ 
④ 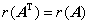 ;
;
⑤ 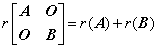 ;
;
⑥ 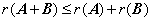 ;
;
⑦ 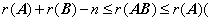 或
或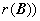 ;
;
若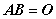 ,则
,则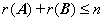 ,其中
,其中 ,
,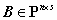 .
.
⑧ 设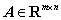 ,则
,则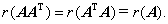
(2) 求矩阵的秩 (理论依据:矩阵的初等变换不改变矩阵的秩)
 (行阶梯形矩阵),
(行阶梯形矩阵),
则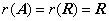 的非零行的个数.
的非零行的个数.
(3) 矩阵的相抵(等价)
① 
② 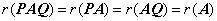 ,其中
,其中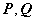 可逆.
可逆.
③ 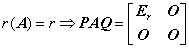 或
或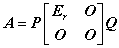 .
.
三、线性空间
1、概念、子空间的验证(非空、加法和数乘的封闭)
2、向量组的线性相关性的判断(命题4.2、4.3、4.4、4.5、定理4.1、4.2、4.4)
(1) 证明方法--定义、秩、坐标化
(2) 充要: 线性相关
线性相关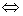 其中至少有一个向量可由其余向量线性表示.
其中至少有一个向量可由其余向量线性表示.
充分: 线性相关
线性相关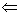 部分向量组线性相关
部分向量组线性相关
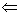 向量的个数
向量的个数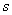 大于向量分量的个数
大于向量分量的个数
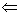
 被个数少于
被个数少于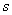 的向量组线性表示
的向量组线性表示
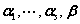 线性无关
线性无关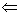

3、等价向量组
(1) (Ⅰ)可由(Ⅱ)线性表示,则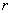 (Ⅰ)
(Ⅰ) 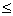
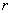 (Ⅱ).
(Ⅱ).
(2) (Ⅰ)与(Ⅱ)等价,则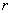 (Ⅰ)
(Ⅰ) 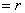 (Ⅱ).
(Ⅱ).
4、向量组的秩及极大无关组(命题4.6)、线性空间的基与维数
(1) 写成列向量作初等行变换.
(2) 对于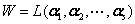 ,则
,则 , 即生成子空间的维数
, 即生成子空间的维数
与基就是向量组 的秩与极大无关组.
的秩与极大无关组.
5、坐标的概念、基变换公式与坐标变换公式
基变换公式: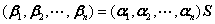
坐标变换公式:
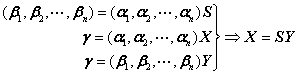 或
或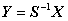
四、线性方程组(含参量、不含参量)
1、解的情况
(1) 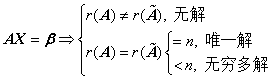
若 是方阵,则
是方阵,则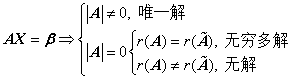
(2) 齐次线性方程组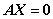 有非零解
有非零解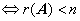 .
.
若 是方阵,则齐次线性方程组
是方阵,则齐次线性方程组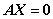 有非零解
有非零解 .
.
2、解的结构
齐次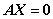 :
:
(1) 解空间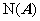 、
、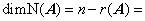 基础解系所含向量的个数
基础解系所含向量的个数
(2) 结构式:通解=基础解系的线性组合
非齐次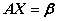 :
:
(1) 非-非=齐
(2) 结构式:通解=特解 导出组
导出组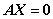 的基础解系的线性组合
的基础解系的线性组合
五、线性变换
1、线性变换的验证 (定义5.4)
2、线性变换在一个基下的矩阵(定义5.7)、命题5.8

3、线性变换在不同基下的矩阵之间的关系(相似) 定理5.9
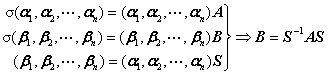
六、内积空间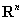
1、内积的概念、长度、正交(正交向量组必线性无关)
2、施密特正交化
3、正交矩阵(定义、性质)
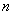 阶实矩阵
阶实矩阵 是正交矩阵的充要条件是
是正交矩阵的充要条件是 的列(行)向量组是
的列(行)向量组是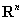 的一个标准正交基.
的一个标准正交基.
七、矩阵的相似对角形
1、特征值和特征向量的定义、性质
2、相似矩阵的定义、性质(迹、秩、行列式、特征值相等)
相似的判定:若 与
与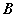 可对角化,且
可对角化,且 与
与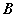 具有相同的特征值,则
具有相同的特征值,则 与
与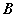 相似.
相似.
3、矩阵的相似对角化
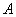 可对角化
可对角化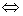
 有
有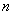 个线性无关的特征向量
个线性无关的特征向量
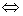 数域
数域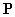 内有
内有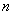 个特征值,每一个特征值的几何重数等于代数重数
个特征值,每一个特征值的几何重数等于代数重数
(充分条件)  有
有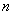 个互不相同的特征值
个互不相同的特征值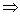
 可对角化
可对角化
4、实对称矩阵
(1) 特征值:实对称矩阵有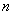 个实特征值.
个实特征值.
(2) 特征向量:实对称矩阵的属于不同特征值的特征向量正交.
(3) 实对称矩阵必正交相似于对角矩阵(几何重数等于代数重数).
(4)  与
与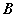 均为实对称矩阵,则
均为实对称矩阵,则 与
与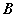 正交相似
正交相似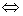
 与
与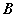 具有相同的特征值.
具有相同的特征值.
(正交相似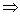 相似、合同)
相似、合同)
八、二次型
1、二次型的矩阵及秩
2、矩阵的合同:合同必相抵;正交相似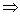 相似、合同
相似、合同
实对称矩阵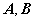 合同
合同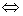
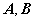 的正惯性指数与秩相同
的正惯性指数与秩相同
3、化二次型为标准形(不唯一)--正交替换法、配方法
4、惯性定理:实二次型的规范形唯一
5、正定二次型
(1) 判定:① 定义;
②  的特征值都大于零(
的特征值都大于零( 的正惯性指数等于
的正惯性指数等于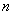 );
);
③  与
与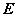 合同(与正定矩阵
合同(与正定矩阵 合同的实对称矩阵
合同的实对称矩阵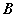 正定);
正定);
④ 存在可逆矩阵 ,使得
,使得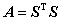 ;
;
⑤  的所有顺序主子式都大于零
的所有顺序主子式都大于零
(2) 必要条件: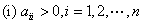 ;
;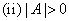
-
线代总结
20xx年X1特征值,特征向量,线性无关X2伴随矩阵,初等变换(初等矩阵)T1矩阵行列式,运用矩阵乘法公式B=AX,则{B}={A…
-
线代总结
1.注意矩阵之间常见的几种关系:(1)可交换(2)等价(3)相似(4)合同其中,等价与相似的符号都是“~”,但他们含义不同,需注意…
-
线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…
-
线性代数公式总结
行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、Aij和aij的大小无关;②、某行…
-
线性代数知识点总结
线性代数知识点总结第一章行列式第一节二阶与三阶行列式把表达式a11a22a12a21称为a11a21a11a12所确定的二阶行列式…
-
加油,祝你成功--线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…
-
线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…
-
线性代数公式总结
行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、Aij和aij的大小无关;②、某行…
-
20xx考研真题线性代数试题特点总结
20xx年x月x日来源:跨考教育分享到:新浪微博搜狐微博腾讯微博网易微博人人网20xx年线性代数依旧是5道考题,两个选择题,一个填…
-
线性代数中必考知识点归纳总结
20xx年线性代数必考的知识点1、行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、…