《数学建模》课程设计

  报   告

课题名称：飞行管理问题   

系（院）：      理学院       

专    业：   数学与应用数学  

班    级：       

学生姓名：      

学    号：           

指导教师：       

 开课时间：  20##-20##  学年  二  学期

飞行管理问题的优化模型

摘要

为了避免较多飞机在区域内会发生碰撞，让飞机在某正方形区域内安全飞行，便于进行飞行管理，所以在飞机飞行过程中，要适当调整各架飞机的方向角（调整幅度尽量小），所以这是个优化问题。

本文我们根据题目所给的数据，利用matlab软件绘制出飞机的位置图标及飞行路径，并利用lingo软件找出了碰撞发生的飞机、碰撞发生的点和时间。同时再寻找判断两架飞机是否会相撞的方法，我们发现可以在飞机飞出区域之前每隔一段较短的时间对飞机进行监控，看是否与别的飞机相撞。

然后，我们根据问题讨论了飞行方向角的调整时间和次数对最优解的影响，发现调整时间越早，调整角度就越小，所以我们决定在第六架飞机刚飞到区域边缘的时候就进行飞行角度的调整，并且达到了优化目标：。

由题意，我们找到约束条件，然后把这些约束条件在lingo中用语言描述出来，再针对运算方面进行改进，得到我们的lingo程序，运行后我们得到了飞机调整的飞行方向角和方案。

关键词：简化，最小调整幅度，最优

一、问题重述

6. 飞行管理问题(优化模型)

在约10000米高空的某边长160km的正方形区域内,经常有若干架飞机作水平飞行.区域内飞行的每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理.当一架欲进入该区域的飞机到达区域的边界时,记录其数据后,须立即判断是否将与区域内的飞机相碰撞.若可能发生碰撞,则应计算如何调整各架飞机的飞行的方向角，以避免碰撞。

作如下假设:

(1)任意两架飞机的安全飞行距离为8公里;

(2)所有飞机的飞行速度为800公里/小时;

(3)进入该区域的飞机在到达区域边界时,与区域内的飞机的距离应在60公里以上;

(4)最多考虑6架飞机;

(5)不必考虑飞机离开此区域后的情况.

请你对这个避免碰撞的飞行管理问题建立数学模型，列出计算步骤，对以下数据进行计算（方向角误差不超过0.01），要求飞机飞行方向角调整的幅度尽量小。

设该区域四个顶点的坐标为：(0,0)，(160,0)，(160,160)，(0,160)

记录数据为：

注：方向角指飞行方向与x轴正向的夹角。

二、问题分析

根据问题容易知道，这显然是一个优化问题，当两架飞机可能发生碰撞时，即在规定区域内某一时刻两架飞机之间的距离小于8公里，因此要调整飞行方向一定角度，保证任意两架飞机在区域内任意时刻，两者的距离均不小于8公里，避免相撞。考虑到调整角度应尽量小，可以简化飞行方向调整策略，降低调整难度，同时减轻机内乘客及工作人员的不适。此外由此初步确定了调整目标：所有六架飞机的飞行方向调整角度均尽量小。

三、模型假设与符号约定

（1）假设飞机进入控制区域后完全服从地面控制台的调度，其他任何因素或人都不能改变飞机的飞行方向角。

（2）假设从飞机管理处发出的信息飞机马上可以接收并执行（此处忽略飞机在执行过程中所需耗费的时间），不存在滞后或延迟，即可以实现实时控制。

（3）不考虑本组设计的程序在实时控制中运行的时间。

 (4) 不碰撞的标准为任意两架飞机的距离大于8km。

（5）所有飞机飞行速度均为每小时800km。

（6）飞机在区域外靠雷达自动与其他飞机保持距离大于60km，进入区域后由地面控制台进行统一控制，保证飞机距离大于8km。

（7）假设飞机在区域内改变方向，在飞出区域后驾驶人员会自觉调整方向回归原航线继续飞行。

（8）为了表达清晰，我们对符号作出以下说明：

四、模型的建立和求解

1、问题简化

明显我们不可能每时每刻都对每架飞机进行调整，当然希望调整的次数越少越好，调整的飞机数越少越好，角度越小越好。

第一，我们需要知道哪些飞机会在飞行过程中与其他的飞机相撞（距离小于8km）。

第二，我们需要调整哪些飞机和多少角度来使最小。

假使飞机要从A点向C飞行，途中想要偏离C点，由图α＜β（外角大于内角），明显是从一开始就改变α角度使得更小，所以越早调整越好，即在第六架飞机进入时即可调整角度。

如图：

2、模型建立

由问题一，我们首先判断在第6架飞机进入正方形区域后会否发生飞机碰撞。

我们依照数据，用matlab画出大致的航线图形（程序见附录1）。其中灰线代表飞机向上飞行，黑线代表飞机向下飞行。（如图1） 

图1：

把飞机速度转化成，由此我们可以知道飞机在5秒内仅飞行1km多，根据这个我们将飞机飞行时间分成5秒一段，由这种分段来达到近乎实时监控的目的，知晓每一架飞机每一个5秒的飞行情况，尽可能精确地求出有可能发生碰撞的飞机及碰撞发生的时间段，方便调整。

我们对这个思路整合后用lingo编出程序（程序见附录2），运行得出结果：如果飞机在区域内按照原飞行方向角沿原航线继续飞行，那么是会发生一次飞机碰撞的。

是在第88个5秒时，第5架和第6架飞机会发生碰撞。

所以需要调整飞机的飞行方向角来避过这次相撞。

下面进行模型求解：

根据题意，目标函数应该为飞行方向角的调整幅度取最小值，所以我们可以得到目标函数：

题目告诉我们，不碰撞的标准为任意两架飞机的距离都大于8。我们将飞机看做一个质点，求出两个质点之间的欧式距离：即为两架飞机间的距离（如图2）：

                          图2

可得到：

，

  

为了方便计算并且更加直观，我们对本题理解为在第6架飞入时飞机管理处便进行计算，将得出的最优调整方案马上提供给飞机执行，即每架飞机最多在t=0时改变一次躲过碰撞，之后在区域内便不再改变方向角。根据这种理解，我们又得到一个约束条件：

    

      

综上分析，可以得到第一个模型：

由此编写lingo程序（见附录3），可知最优解为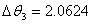°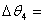，-0.4954°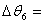，1.567°（其他调整角度为0）使得最小。

五、模型改进与推广

模型优点：在调整各飞机偏转的方向角时，我们只调整少数飞机，能把问题的计算简单化，而且借助各架飞机初始位点的运动路线，更直观地初步判断各飞机于某时刻的基本碰撞情况。

模型缺点：1这个模型是平面的，尚未考虑空间上的问题。2在这个模型中我们没有考虑飞机接受命令到执行命令之间的时间，事实上这段时间是存在且不可忽略的。3在实际的飞机航行中，改变飞行角度后，飞机便离开了原航线，在以后的飞行中是要矫正过来的，但是在我们的模型中这个问题并没有列入考虑范围。4在飞机的飞行过程中，它会受到风速、仪器、天气的影响，进而导致飞行员在调整角度的过程中可能出现偏差。

并且在模型求解过程中用lingo求解最优解时，程序运行时间有些长，这在现实中是没有那么多的等待时间，因为飞机也在飞行，坐标还在改变，所以模型求解时间应越短越好。

模型推广：此类模型可以用于航海中轮船及各种相遇问题等。总体来说这个模型比较简单易懂，符合一般的调整需要，不足的是模型需要强大的实时数据支持。

六、参考文献

[1]朱道元，《数学建模精品案例》，南京：东南大学出版社，1999

[2]程极泰，《最优设计的数学方法》，北京：国防工业出版社，1994

附录

（1）

x1=150;

y1=140;

a1=243;

b1=y1-x1*tan(a1/180*pi);

xa=1:5:160;

ya=xa*tan(a1/180*pi)+b1;

plot(xa,ya,'r',x1,y1,'+')

hold on

x2=85;

y2=85;

a2=236;

b2=y2-x2*tan(a2/180*pi);

xb=1:5:160;

yb=xb*tan(a2/180*pi)+b2;

plot(xb,yb,'r',x2,y2,'+')

hold on

x3=150;

y3=155;

a3=220.5;

b3=y3-x3*tan(a3/180*pi);

xc=1:5:160;

yc=xc*tan(a3/180*pi)+b3;

plot(xc,yc,'r',x3,y3,'+')

hold on

x4=145;

y4=50;

a4=159;

b4=y4-x4*tan(a4/180*pi);

xd=1:5:160;

yd=xd*tan(a4/180*pi)+b4;

plot(xd,yd,'g',x4,y4,'+')

hold on

x5=130;

y5=150;

a5=230;

b5=y5-x5*tan(a5/180*pi);

xe=1:5:160;

ye=xe*tan(a5/180*pi)+b5;

plot(xe,ye,'r',x5,y5,'+')

hold on

x6=0;

y6=0;

a6=52;

b6=y6-x6*tan(a6/180*pi);

xf=1:5:160;

yf=xf*tan(a6/180*pi)+b6;

plot(xf,yf,'g',x6,y6,'+')

axis([0 160 0 160])

hold on

（2）

model:

sets:

jiaodu/1..6/:a,a1,b,k,s,c,x,y;

bianhua/1..204/:t;

zuobiao(jiaodu,bianhua):x1,y1;

chongdie(jiaodu,jiaodu):cu;

juli(bianhua,jiaodu,jiaodu):ju;

jiao/1..3/:ja;

endsets

@for(bianhua(i):

   t(i)=5*i;

);

@for(jiaodu(i):@free(k(i));

@free(s(i));

@free(c(i)););

@for(jiaodu(i):@free(a1(i));

@free(b(i)););

@for(jiaodu(i):

@for(bianhua(j):@free(x1(i,j));

@free(y1(i,j));););

min=(@sum(jiaodu(i):a1(i)));

@for(jiaodu(i):@bnd(-30,a1(i),30););

@for(jiao(e):a1(6)=-3+e;

@for(jiao(z):a1(3)=-2+z;

@for(jiaodu(i):

a(i)=a(i)+a1(i);

k(i)=@tan(a(i)/180*3.14159);

c(i)=@cos(a(i)/180*3.14159);

b(i)=y(i)-x(i)*k(i);

);

@for(jiaodu(i):

@for(bianhua(j):

x1(i,j)=x(i)+c(i)*t(j)*800/3600;

y1(i,j)=k(i)*x1(i,j)+b(i);

);

);    

@for(bianhua(i):

@for(chongdie(j,p): 

cu(j,p)=@if(j #eq# p,66,1);

ju(i,j,p)=(cu(j,p)*((x1(j,i)-x1(p,i))^2+(y1(j,i)-y1(p,i))^2+1))^(1/2);

);

);

););

data:

x=150 85 150 145 130 0;

y=140 85 155 50 150 0;

a=243 236 220.5 159 230 52;

enddata

（3）

model:

sets:

feiji/1..6/:a,a1,a2,x,y,v;

shijian/1..204/:t;

zuobiao(feiji,shijian):xt,yt;

ok(feiji,feiji):f;

endsets

min=@sum(feiji(i):@abs(a2(i)););

@for(feiji(i):a1(i)=a(i)/180*3.14159;);

@for(shijian(i):t(i)=i/720;);

@for(shijian(k):

@for(ok(i,j) | i #lt# 6 #and# j #gt# i:

(x(i)+v(i)*t(k)*@cos(a1(i)+a2(i))-(x(j)+v(j)*t(k)*@cos(a1(j)+a2(j))))^2+(y(i)+v(i)*t(k)*@sin(a1(i)+a2(i))-(y(j)+v(j)*t(k)*@sin(a1(j)+a2(j))))^2＞64;

);

);

@bnd(0,a2(1),0);

@bnd(0,a2(2),0);

@bnd(-0.2,a2(3),0);

@bnd(0,a2(4),0.1);

@bnd(0,a2(5),0);

@bnd(0,a2(6),0.2);

data:

x=150 85 150 145 130 0;

y=140 85 155 50 150 0;

a=243 236 220.5 159 230 52;

v=800 800 800 800 800 800;

enddata

end

 

第二篇：数学建模(飞行管理问题)

飞行管理问题

摘要   让飞机在某正方形区域内安全飞行，便于进行飞行管理，所以在飞机飞行过程中，要适当调整各架飞机的方向角（调整幅度尽量小），以避免发生碰撞。本文通过对两两飞机飞行过程最小临界距离大于8km为入手点，以时刻后飞机所处状态为研究对象。通过点的向量平移，找出临界距离（8km）视为界点，再通过两点距离公式列出一元二次不等式，转化为一元二次方程根的情况，判断的取值。

当＜0时，说明方程无实数解，即该两飞机不会碰撞。当≥0时，说明方程有实数解，且可以求出对应的值，看是否在规定区域范围内（0≤≤0.283h）。若t不在范围内，说明两飞机在规定区域不会发生碰撞，而在区域范围外会发生碰撞（不在我们考虑范围内）若在所规定范围，说明两飞机会在区域范围内发生碰撞，此时应调整各架飞机的方向角。方向角的调整虽然在30内有足够空间（相应的可行解就很多），但又要求所调整的幅度尽可能小（就要求我们求出相应的最优解），故当调整一架飞机方向角后，应该对应判断该飞机与其余各飞机是否会发生碰撞。

最后，我们对模型的优缺点和改进方向作了分析。

关键词    向量平移     最短临界距离    方向角    调整幅度 

一、问题重述（略）

二、模型假设：

（1）不碰撞的标准为任意两架飞机的距离大于8km

（2）飞机飞行方向角调整的幅度不应超过30

（3）所有飞机飞行速度均为每小时800km

（4）进入该区域的飞机在到达该区域边缘时，与区域内的距离应在60km以上

（5）最多需要考虑6架飞机

（6）不必考虑飞机离开此区域后的状况

（7）飞机调整方向角后，不受偏转弧度的影响

（8）每架飞机在调整角度后都沿调整后的方向角飞出区域外

（9）新进入的飞机在进入区域的瞬间，不考虑计算机记录时的时间间隔飞机所飞行的距离（即该时间间隔忽略不计）

（10）每架飞机都视为质点

三、符号说明：

    表示飞机编号（=1,2,3,4,5,6）

      表示第架飞机所处位置的横坐标

    表示第架飞机所处位置的纵坐标

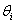      表示第架飞机的初始方向角

   表示第架飞机所调整的方向角

      表示各架飞机飞行过程达到最短临界距离所用时间

      表示时刻后第架飞机与第架飞机的距离（i≠j）

    表示第架飞机初始记录的点的坐标

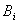    表示第架飞机经时刻后的点的坐标

ai       表示第Ai点经过时刻后所平移的向量

四、模型建立与求解

由假设（1），我们简单分析两架飞机的情形，最终直接运用于多架飞机的情形，题目要求飞机间两两不碰撞。首先我们在不调整各架飞机方向角时，按各飞机初始位点来判断各飞机的碰撞情况，从图（一）中可以大致估算两两飞机在区域范围内的飞行情况，从而可以初步预测和排除部分飞机的碰撞情况。

每架飞机在区域范围内飞行的时间范围为[0，0.283]h，即从原点沿正方形区域对角线飞出的飞机所用时间最大为0.283h。平移向量为ai=（vtcosi,vtsini），Ai=(xi,yi),Bi=(xi+vtcosi,yi+vtsini)

我们建立初始模型: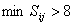，或(i,j=1,2,3,4,5,6 i≠j)

0≤t≤0.283h

问题转化为：

        0≤t≤0.283h

用上述不等式判断初始时刻两两飞机的碰撞情况，

 

图（一）

即    

进而有：

因为＞0，所以可以求出一元二次方程

的两个根=0.13h,=0.14h

、[0，0.283]，可知6、3飞机会在[0.13，0.14]时间范

围内发生碰撞。

即         

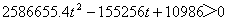
因为＜0，所以一元二次方程

无实数解，即4、3飞机不会发生碰撞。

同理，可以判断，其余各架飞机按初始方向角飞行的碰撞情况如表（一）所示：(T表示会发生碰撞，F表示不会发生碰撞)

表（一）

从图（一）初位点可以直观看出，当6增大时，它与原来不发生碰撞的飞机1、2仍保持不碰撞，又6的可调范围为30内，此时以6=30，其余飞机保持原来的方向角不调整进行计算，可使得每架飞机都不发生碰撞。但要使方向角的调整幅度尽量小，应该尽量让每架飞机都进行稍微的调整。下面我们给定6=5.00并判断出6与3、5飞机不发生碰撞，但此时6与4会发生碰撞，则我们只需对应给4=5.00就可保证6与4不发生碰撞。从而有表（二）调整方式：

表（二）

最终模型：

  

0≤≤0.283h

V=800km/h

五、模型的优缺点与分析

优点：在调整各飞机偏转的方向角时，我们只调整少数飞机，能把问题的计算简单化，而且借助各架飞机初始位点的运动路线，更直观地初步判断各飞机于某时刻的基本碰撞情况。

缺点：调整各飞机方向角时，只调整少数飞机，使得要调整的方向角幅度较大，所以找到的角度不能达到最优，只是可行解。假设（9）中过于理想化，与实际的情况还有一定差距，比如，在飞机的飞行过程中，它会受到风速、仪器、天气的影响，进而导致飞行员在调整角度的过程中可能出现偏差。

六、模型推广

此类模型可以用于航海中轮船的相遇问题等

参考文献  

【1】姜启源、谢金星、叶俊，数学模型 第三版, 北京；高等教育出版社，2003

【2】黄忠裕，初等数学建模, 成都：四川大学出版社，2004.12