实验一

教师审批：

学   号：**********                           班  级：* * * *

实验日期:20##-12-14                       实验人：  * * *

题目二  

                              

【实验目的】

1掌握正态分布的有关计算

2掌握正态分布在实际问题处理中的应用

3掌握数据分析的一些方法和 MATLAB 软件在概率计算中的应用

【实验要求】

掌握综合使用 MATLAB 的命令解决实际问题的方法

【实验内容】

1) 咖啡厂生产 1 磅（约 0.4536kg）重的罐装咖啡，自动包装线上大量数据表明每罐重量服从标准差为 0.1 的正态分布，为了使每罐重量少于 1 磅的产品不多于 10%，应把自动包装线控制的均值 调节到什么位置上？

2) 一台新包装机的价格是 10 万元，但包装的咖啡重量服从标准差为 0.025 的正态分布，同样为了使每罐重量少于 1 磅的产品不多于 10%，应把自动包装线控制的均值 调节到什么位置上？

【实验方案】

1、  由于第 （1）问和第（2）问为同一类问题，故可建立以M文件以简便程序。

2、  由题设每罐咖啡质量，题目要求在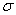一定时，求出，使。那么分析得，且越大，p越大。

3、  为此先令等于1，使用while 循环，调用normcdf函数求出该值下的概率值p，与比较，若p<,则加上一较小值0.00001，变为，算出值下的概率，继续与比较，如此循环直到>,此时的在误差允许范围内即为所求

【实验过程】

1、建立M文件，程序代码如下

function [f3]=fun3(p,sigma)

mu=1;

fx=1;

while(fx>p)

    fx=normcdf(1,mu,sigma);

    mu=mu+0.00001;

end

fprintf('mu=%.5f',mu)

2、主程序调用fun3函数，程序代码及运行结果如下：

1）>>  fun3(0.1,0.1)

mu=1.12817 >>

2）>>  fun3(0.1,0.025)

mu=1.03205>>

3、故在误差允许范围内两问分别为：1.12817、1.03205

【小结】

思考：本题两问类似，只是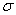不同，因此实验中建立了M文件得到简化Matlab程序代码的功能，也能体现“分类思考”的学习方法，从实际中提取有用信息，建立模型求解。此外建立M文件还能使程序更为清晰，更易理解。

心得体会： 1、实验过程中，发现对Matlab中的命令函数不熟悉，导致一些不必要的麻烦。所以以后必须在实验之前做好充分准备，熟悉实验。

2、对于Matlab软件的Help应用不熟悉，不能充分利用Help帮助文件解决问题。

 问题五         

                         

【实验目的】

1加深对中心极值定理的认识，对其背景和应用有直观的理解

2了解 MATLAB 软件在模拟仿真中的应用

【实验要求】

中心极值定理的理论知识，Matlab软件

【实验内容】

  根据孟德尔遗传理论，红、黄两种番茄杂交，第二代红果植株和黄果植株的比例为3 ：1 ，

 现在种植杂交种400 株，试求黄果植株介于 83——117 之间的概率。

【实验方案】

对每一株番茄来说，考察其是否为黄果植株相当于进行啦一次贝努利实验。由于每株是否为黄果植株相互独立，本实验即相当于进行啦400次贝努利实验。如设X为黄果植株的株数，则，其中试验次数n=400,每次试验的概率p=0.25,那么np=100。

根据中心极值定理知道，，现要求,由以上分析得：

本实验通过Matlab软件实现求解概率。

【实验过程】

a)      采用中心极值定理近似为正态分布。

>> p=normcdf(17/(75)^(1/2),0,1)- normcdf(-19/(75)^(1/2),0,1)

p =

0.9611

b) 直接利用二项分布求得：

>> px=binocdf(117,400,0.25)-binocdf(83,400,0.25)

px =

    0.9621

两种方法求得的概率误差较小，但是方法一体现了中心极值定理的应用。可以认为黄果植株介于 83——117 之间的概率p=0.9611

【小结】

思考：试验中采用了两种方法求解概率，但是方法一利用中心极值定理近似计算，方法二则直接利用Matlab命令直接计算，可以看出两者结果相差不大。以一实例证明啦中心极值定理的正确性。但是方法二只是利用啦计算机强大的计算能力，若人工计算则相当繁琐；二方法一则可以通过查正态分布表求解概率，在实验精度不是特别高的情况下，优先采用方法一。

  

   实验二

教师审批：

 学  号：**********                                 班  级：* * * *

实验日期:20##-12-21                                实验人：  * * *

题目一

                            

【实验目的】

1掌握两个正态总体方差比的区间估计方法

2会用MATLAB 软件求两个正态总体方差比的区间估计

【实验要求】

参数估计理论知识

两个正态总体区间估计的理论知识

Matlab软件

【实验内容】

从甲乙两个蓄电池厂生产的产品中，分别抽取10个样品，测得他们的电容来那个为：

甲厂：146;141;138;142;140;143;138;137;142;137

乙厂：[141;143;139;139;140;141;138;140;142;136

若蓄电池的电容量服从正态分布，求两个工厂生产的蓄电池的电容量的方差比的置信水平为0.90的置信区间。

【实验方案】

由主教材定理5.10知道，

选取，使这里使满足使满足，

求得

整理可得

则置信区间

【实验过程】

1、建立M文件，程序代码如下：

function [down,up]=fun1(X,Y)

s1=std(X);

s2=std(Y);

alpha=0.1;

[m1,n1]=size(X);

[m2,n2]=size(Y);

Sum1=m1*n1-1;

Sum2= m2*n2-1;

down=s1/(s2*sqrt(finv(1-alpha/2,Sum2,Sum2)));

up=s1/(s2*sqrt(finv(alpha/2,Sum1,Sum1)));

fprintf('down=%.4f     up=%.4f',down,up);

2、主程序调用fun1函数，程序代码及运行结果如下：

程序代码

clc;clear;

X=[146;141;138;142;140;143;138;137;142;137];

Y=[141;143;139;139;140;141;138;140;142;136];

fun1(X,Y);

运行结果

down=0.8175     up=2.5989>>

由程序运行结果可以得到，两个工厂生产的蓄电池的电容量的方差比的置信水平为0.90的,置信区间为（0.8175，2.5989）

【小结】

  心得体会：1、实验过程中，发现对Matlab中的命令函数不熟悉，导致一些不必要的麻烦。应当学会Help帮助文件的利用。

  2、finv函数是已知概率求随机数，而查F分布表是用上侧分位数得到的。开始并未注意到，导致区间上下界刚好相反。通过实验，加深了对F分布表以及Matlab程序命令的认识。

                          题目二                               

【实验目的】

1会用Matlab软件进行单个总体均值、方差的假设检验

2会用Matlab软件进行两个总体均值差、方差比的假设检验

【实验要求】

掌握综合使用 MATLAB 假设检验的基本命令和基本操作

【实验内容】

某厂生产的保险丝，其融化时间服从N(,取10根，测得数据为：, 

42;65;75;79;59;57;68;54;55;71。问：是否可以认为整批保险丝的融化时间的方差偏大？（取0.05）

【实验方案】

已知 现假设：

    

在为真的情况下，检验统计量

拒绝域为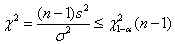

由样本值算出统计量的观察值。若则拒绝，即认为总体方差不偏大，否则接受即认为总体方差偏大。

【实验过程】

1、建立M文件，程序代码如下：

function [chi1,chi2]=fun2(X,sigma,alpha)

[m,n]=size(X);

sum=m*n;

s2=std(X)^2;

%chi1表示统计量的观察值；

chi1=(sum-1)*s2/(sigma^2)

%chi2表示拒绝域的临界值;

chi2=chi2inv(alpha,sum-1);

fprintf('chi1=%.4f,   chi2=%.4f,' ,chi1,chi2);

2、主程序调用fun2函数，程序代码及运行结果如下:

程序代码

>> clc;clear;

 X=[42;65;75;79;59;57;68;54;55;71];

fun2(X,80,0.05);

运行结果

chi1=0.1763,   chi2=3.3251

由于chi1=0.1763< chi2=3.3251,所以拒绝,接受，即整批保险丝的融化时间的方差正常，不偏大。

【小结】

心得体会：实验中关键在于理清其逻辑关系，搞清楚拒绝域是什么。开始时未能正确找出拒绝域，导致实验结果（) 不正确，虽没有影响最终结果，但是方法不正确，属于侥幸。应当认真研读教材，做一些典型题目，加深对假设检验方法的理解。

 

第二篇：概率论上机实验报告

西安交通大学

概率论上机实验报告 ------------------用蒙特卡洛算法计算积分

吴建东

2011/12/14

蒙特卡罗算法思想：当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解

概率论上机实验报告 能动04 吴建东 10031102

题目:

一． 用蒙特卡洛方法估计以下积分值

1.2∫3xdx 2.

12∫

x2π/20xsinxdx 3. 2∫+∞0e?x2dx 二. 利用蒙特卡洛方法估计下列积分：

1. ∫e

0dx 2. ∫01+x2

要求： ① 针对要估计的积分选择适当的概率分布，并设计蒙特卡洛估计

算法。

② 利用计算机产生所选分布的随机样本以估计积分值。

③ 通过计算均分误差或者概率方差（标准差）对估计结果进行评

价。

蒙特卡罗算法思想：当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。

蒙特卡洛算法的理论依据

1.E(g(x))=∫g(x)f(x)dx 其中f(x)为随机变量X的概率密度函数。若设随机变量Y=g(X) 将一个积分问题变成求随机变量Y的数学期望。

2.利用大数定理以及参数估计，用若干组样本均值来估计随机变量的数学期望，当样本容量比较大时，样本的均值与理论随机变量的误差很小。

利用MATLAB软件产生服从某个概率密度函数的若干组样本，之后求出样本的均值，也可以求出方差。

一．用蒙特卡洛方法估计以下积分值

1.2

3∫3xdx 2. 2∫π/20xsinxdx 3. ∫+∞0e?x2dx 1. 算法分析 ： 我们假设随机变量X服从 [2,3]上的均匀分布即X~U（2,3）,则∫2x2dx即E（x2）,因此将一个求积分问题变成求期望的问题。

设：g(x)=x2

1 x∈[2,3]f(x)=? 0 其他

- 1 -

概率论上机实验报告 能动04 吴建东 10031102

根据数理统计学知识以及大数定理，当样本容量足够大是可以用样本的均值去估计随机变量的期望，将求期望问题变成求若干组样本均值问题。我们通过和理论计算值进行比较得到误差，同理可以得到方差，以此评价该算法。

Matlab 编程如下：

x=rand(100,1000)+2; % 产生100组满足条件的随机变量，每组1000个 y=x.^2;

corz=19/3; % 精确计算值 z=sum(y,2)/1000; %求 y 的期望

b=abs(z-ans).^2; 每一组样本与该组样本期望的差的平方

ans=sum(z,1)/100 % 求所有组的期望

fangcha=sum(b,1)/99 % 求方差

plot(z) %画出每一组样本的均值。

程序运行结果如下：

ans（估计结果）= 6.3346

误差为 0.0013

Fangcha（方差） 0.0026

图表 1 1.1题的计算结果

100个样本平均值 如下图 结果集中在6.3-6.4之间

- 2 -

概率论上机实验报告 能动04 吴建东 10031102

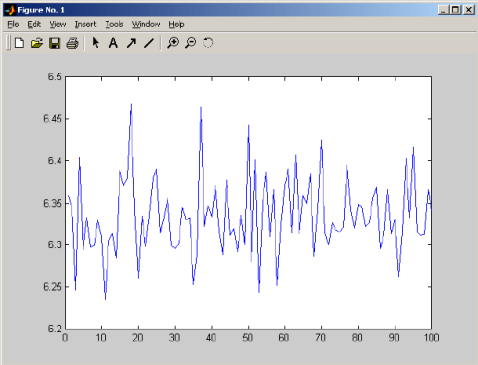
我们只取了1000随机数作为样本，求出100个样本估计值的均值作为积分的概图表 2 1.1题的结果作图

率估计，显然样本容量较小。但是通过结果以及图像说明此时误差已经达到很小了，而且结果也比较稳定。

2.

本题思路同上，首先产生若干组按在[0，2上的均匀分布的简单随机样本，然后计算样本对应的y=xsinx的值，求出y的均值，最后用样本的均值估计随机变量的期望。即得到一个积分值的估计，求出若干组估计值根据其计算出估计值的均值，得到最后的估计。用此估计和正确值比较。

设：g(x)=xsinx

， x∈?0,?f(x)=?

0 其他

本题目需要注意求期望时千万不要忘记乘以概率密度。

Matlab 编程如下；

x=rand(100,1000)*pi/2; % 产生100组满足条件的随机变量，每组1000个 y=x.*sin(x);

corz=1; % 精确计算值 z=sum(y,2)/1000*pi/2;

- 3 -

概率论上机实验报告 能动04 吴建东 10031102

b=abs(z-ans).^2;

ans=sum(z,1)/100

fangcha=sum(b,1)/99 plot(z)

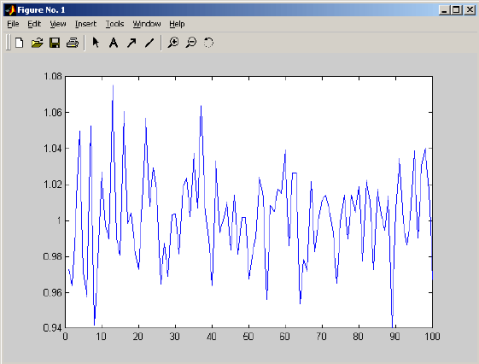
作出图形如下：

图表 3 1. 2题的结果作图

运行结果

ans=1.0013

wucha=0.0013 fangcha=0.0069

如上小题，虽然样本容量不大但是估计精度已经很小，足以说明该算法的强大。

3.分析：题目中因为积分区间无限故不能使用均匀分布，此时可以利用matlab产生正态分布模拟。此次产生1000组每组100个的样本，观察此次的误差及方差。

+∞

∫e

0?x21dx=∫g(x)f(x)dx=∫2π2?∞

设：g(x)=+∞1?x2edx 2π π

2

f(x)=

1?x2 x∈(?∞,+∞) e2- 4 -

概率论上机实验报告 能动04 吴建东 10031102

程序如下

x=randn(100,1000); %产生满足正态分布的100组每组1000个样本的简单随机样本 x_aver=sum(x,2)/1000;

e=exp(-x_aver.^2);

ans=sqrt(pi/2)*e;

plot(ans)

ans_aver=sum(ans,1)/100

corans=sqrt(pi/2)

wucha=abs(ans_aver-corans)

fangcha=(ans-corans).^2;

fangcha=sum(fangcha,1)/99

运行结果：

ans_aver =1.2520

corans = 1.2533

wucha = 0.0013

fangcha =0.0020

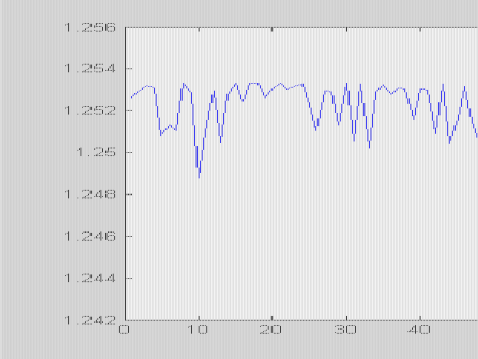
作出图形如下：

图表 4 1.3题的作图结果

尽管这次只有每组中只有1000个样本，得到的估计值集中在1.25到1.253之间，误差比较小，方差也比较小。

二. 利用蒙特卡洛方法估计下列积分：

- 5 -

概率论上机实验报告 能动04 吴建东 10031102

12

x21. ∫e

0dx 2. ∫01+x2

本大题中两个积分均不能用简单积分方法求出其原函数，只能通过具体数值（即数值积分）求其数值解。

1. 解：

1

∫e

0x21dx=∫g(x)f(x)=∫e?1dx0x2

g(x)=e

f(x)=?1 x∈[0,1] 0 其他 x2编写程序如下：

x=rand(100,1000);

y=exp(x.^2);

y_aver=sum(y,2)/1000;

ans=sum(y_aver,1)/100

fangcha=(y_aver-ans).^2;

fangcha=sum(fangcha,1)/99

plot(y_aver)

作出图像如下：

- 6 -

图表 5 2.1题的作图结果

概率论上机实验报告 能动04 吴建东 10031102

运行结果：

ans =1.4627

fangcha = 0.0171

2

2. ∫01+x22=∫01?dx+x22

g(x)=2

+x22 故设

编写程序如下： f(x)=?

x=rand(100,1000)*2;

y=sqrt(1+x.^2);

y=2./y;

y_aver=sum(y,2)/1000;

ans=sum(y_aver,1)/100

fangcha=(y_aver-ans).^2;

fangcha= sum(fangcha,1)/99

plot(y_aver)

运行结果如下：

ans =

1.4428

fangcha =

1.4938e-004

作出图像如下：

结果分析：在这两个小题中通过蒙特卡洛算法构造出满足特定分布的若干随机样本，用此样本求某个随机变量的均值进而估计其期望。此方法简单，运行容易，可以作为求某些超越函数的积分方法。

增加样本数目，可提高计算精度，但计算时间也会提高。 0 其他 1 x∈[0,2]2

- 7 -

概率论上机实验报告 能动04 吴建东 10031102

0102030405060708090100

图表 6 2.2题的作图结果

结论：此算法的关键是寻找合适的f(x)与g(x)，选择合适的分布。一旦构造出合适期望函数及概率分布函数，并且可以通过一定手段进行若干次独立重复实验，样本均值即可计算，产生估计结果。经上述各题检验，此算法有很强的优越性，适用范围很广。

增加样本的容量显然可以提高精度，但是运算时间也会增加。改进算法也可以提高精度，例如采取重点抽样，分层抽样以及关联抽样。但是根据我们的结果分析，采取平均值抽样精度已经很高了。

- 8 -