matlab实验报告
数学实验报告
班级: 学号: 姓名:
实验序号:1 日期:年 月 日
实验名称:特殊函数与图形
u 问题背景描述:绘图是数学中的一种重要手段,借助图形,可以使抽象的对象得到明白直观的体现,如函数的性质等。同时,借助直观的图形,使初学者更容易接受新知识,激发学习兴趣。
u 实验目的:本实验通过绘制一些特殊函数的图形,一方面展示这些函数的特点属性,另一方面,就 Matlab 强大的作图功能作一个简单介绍。
实验原理与数学模型:
1、 球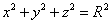 ,x=Rsin
,x=Rsin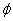 cos
cos , y= Rsin
, y= Rsin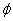 sin
sin , z= cos
, z= cos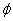 , 0
, 0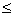

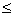 2
2 , 0
, 0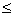
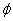
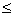

环面 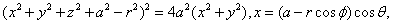
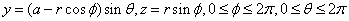
2、 平面摆线: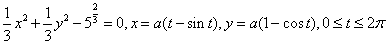
3、 空间螺线:(圆柱螺线)x=acost , y=asint , z=bt ;(圆锥螺线)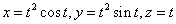
4、 椭球面
双叶双曲面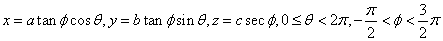
双曲抛物面
实验所用软件及版本:mathematica(3.0)
主要内容(要点):
1、 作出下列三维图形(球、环面)
2、 作出下列的墨西哥帽子
3、 作出球面、椭球面、双叶双曲面,单叶双曲面的图形
4、 试画出田螺上的一根螺线
5、 作出如图的马鞍面
6、 画出Riemann函数的图形
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等):
1) p1=ParametricPlot3D[{sin[u]*cos[v],sin[u]*sin[v],cos[u]},{u,0,pi},{v,0,2*pi}]
p2=ParametricPlot3D[{3*cos[y]-sin[x]*cos[y],3*sin[y]-sin[x]*sin[y],cos[x]},{x,0,2*pi}]
Show{p1,p2}
2)[x,y]=meshgrid(-8:0.5:8);
r=sqrt(x.^2+y.^2)+eps;
z=sin(r)./r;
mesh(X,Y,Z)
axis square
3) 球面 ParametricPlot3D[{sin[u]*cos[v],sin[u]*sin[v],cos[u]},{u,0,pi},{v,0,2*pi}]
椭球面ParametricPlot3D[{5*sin[u*cos[v],4*sin[u]*sin[v],3*cos[u] },{u,0,pi},{v,0,2*pi}]双叶双曲面 ParametricPlot3D[{5*tan[u]*cos[v],5*tan[u]*sin[v],5*sec[u]},{v,-0.5*pi,1.5*pi},{v,0,2* pi}]
双曲抛物面 ParametricPlot3D[{5*u*secv,5*u*tanv,10* },{u,-0.5*pi,0.5*pi },{v,-0.5*pi,0.5*pi}]
},{u,-0.5*pi,0.5*pi },{v,-0.5*pi,0.5*pi}]
4) ParametricPlot3D[{Sqrt[t]cos[t],Sqtr[t]sin[t],0.5*t},{t,0,10*pi}]
5)[x,y]=meshgrid(-25:1:25);
z=x.^2/9 - y.^2/4;
z=sin(r)./r;
surf(X,Y,Z)
title('马鞍面')
grid off
6) n=40; dots={};
For [i=2,i<=n,i++,
For[j=1,i
If [GCD[I,j]==1,AppendTo[dots,{j/I,1/i}]]]]
PP=LisPlot[dots,PlotRange->{0,0.6},PlotStyle->PointSize[0,0.15],
Axeslabel->{“x”,”R(x)”},AspectRatio->0.6]
情况记录
6)中:开始把函数写成{t*cos[t],t*sin[t],t^2},结果画出了圆锥螺线。后来写成{sqrt[t]*cos[t],sqrt[t]*sin[t],1/2*t},画出了图像,发现曲线上升太快,不想田螺上的螺线,经过调整,把z方向的t压缩成0.5*t
圆锥螺线{t^2*cos[t],t^2*sin[t],t}
实验结果报告与实验总结:
1、2、3、4、5较为顺利
6遇到了一些困难,但最后也得到了较好的结果,在整个实验过程中,经常应有ctrl+k,避免了拼写错误。对应用Mathematica作图有了初步了解。实践证明,Mathematica作图功能十分强大,特别对隐函数的作图,可以给人直观的了解。
思考与深入:
对已有县城参数表示的图形实验进行的较为顺利,但对其他图形需花较多的功夫。实践中发现自己对立体几何
解析几何的学习尚需加强,空间想象能力尚需提高。对Mathematica图形显示中的许多修饰函数还缺乏了解,在今后的应用中还要不断了解。
教师评语
数学实验报告
实验序号:2 日期:年 月 日
实验名称:定积分的近似计算
u 问题背景描述:定积分计算的基本公式是牛顿-莱布尼茨公式。但当被及函数的原函数不知道时,如何计算?这时就需要利用近似计算。特别是在许多实际应用中,被积函数甚至没有解析表达式,而是一条实验记录曲线,或一组离散的采样值,此时只能用近似方法计算定积分。
u 实验目的:本实验主要研究定积分的三种近似计算算法:矩形法、梯形法和抛物线法。同时介绍Matlab计算定积分的相关函数。
实验原理:
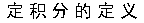

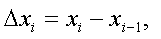
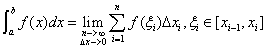
矩形法

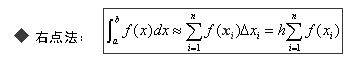




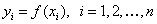


实验所用软件及版本:mathematica(3.0)
主要内容(要点):
2、 分别用梯形法与抛物线法,计算  ,将积分区间[1,2]作120等分。并尝试直接使用函数trapz()、quad()进行计算求解,比较结果的差异。
,将积分区间[1,2]作120等分。并尝试直接使用函数trapz()、quad()进行计算求解,比较结果的差异。
3、 试计算定积分 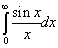 (注意:可以运用trapz()、quad()或附录程序求解吗?为什么?)
(注意:可以运用trapz()、quad()或附录程序求解吗?为什么?)
6 学习fuluBsum.m的程序设计方法,尝试用函数sum改写矩形法和抛物线法的程序,避免for 循环。
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等):
2):梯形法
format long
n=120;a=1;b=2;
syms x fx
fx=1/x;
i=1:n;
xj=a+(i-1)*(b-a)/n;
xi=a+i*(b-a)/n;
fxj=subs(fx,’x’,xj);
fxi=subs(fx,’x’,xi);
f=(fxi+fxj)/2*(b-a)/n;
inum=sum(f)
integrate=int(fx,1,2)
integrate=double(integrate)
fprintf(‘The relative error between inum and real-value is about:%\n
n’,…
abs((inum-integrate)/integrate))
抛物线法
format long
%2*n=120;
n=60;
a=1;b=2;
syms x fx
fx=1/x;
i=1:n;
x0=a+(2*i-2)*(b-a)/(2*n);
x1=a+(2*i-1)*(b-a)/(2*n);
x2=a+(2*i-0)*(b-a)/(2*n);
fx0=subs(fx,x,x0);
fx1=subs(fx,x,x1);
fx2=subs(fx,x,x2);
si=(fx0+4*fx1+fx2)*(b-a)/(6*n);
inum=sum(si)
integrate=int(fx,1,2);
integrate=double(integrate)
fprintf('抛物线法的相对误差为:%e\n',abs((inum-integrate)/integrate))
trapz();
x=1:1/120:2;
y=1./x;
trapz(x,y)
quad(‘1./x’,1,2)
3 、使用函数trapz()
x=1:1/120:inf;
y=sin(x)/x;
trapz(x,y)
使用函数quad()
Quad(‘sin(x)./x’,0,inf)
矩形法
format long
n=inf;a=0;b=inf;
syms x fx
fx=sin(x)/x;
i=1:n;
xj=a+(i-1)*(b-a)/n;
xi=a+i*(b-a)/n;
fxj=subs(fx,’x’,xj);
fxi=subs(fx,’x’,xi);
fxij=subs(fx, ’x’,(xi+xj)/2);
f=fxij*(b-a)/n;
inum=sum(f)
integrate=int(fx,0,1)
integrate=double(integrate)
fprintf(‘The relative error between inum and real-value is about:%\n
n’,…
abs((inum-integrate)/integrate)
使用matlab命令
syms x;f=sin(x)/x;I=int(f,0,inf)
6 、使用求和函数
矩形法
format long
n=100;a=0;b=1;
syms x fx
fx=1/(1+x^2);
i=1:n;
xj=a+(i-1)*(b-a)/n;
xi=a+i*(b-a)/n;
fxj=subs(fx,’x’,xj);
fxi=subs(fx,’x’,xi);
fxij=subs(fx, ’x’,(xi+xj)/2);
f=fxij*(b-a)/n;
inum=sum(f)
integrate=int(fx,0,inf)
integrate=double(integrate)
fprintf(‘The relative error between inum and real-value is about:%\n
n’,…
abs((inum-integrate)/integrate))
抛物线法
format long
%2*n=200;
n=100;
a=0;b=1;
syms x fx
fx=1/(1+x^2);
i=1:n;
x0=a+(2*i-2)*(b-a)/(2*n);
x1=a+(2*i-1)*(b-a)/(2*n);
x2=a+(2*i-0)*(b-a)/(2*n);
fx0=subs(fx,x,x0);
fx1=subs(fx,x,x1);
fx2=subs(fx,x,x2);
si=(fx0+4*fx1+fx2)*(b-a)/(6*n);
inum=sum(si)
integrate=int(fx,0,1);
integrate=double(integrate)
fprintf('抛物线法的相对误差为:%e\n',abs((inum-integrate)/integrate))
情况记录
1、 梯形法和抛物线法程序设计较为顺利。但要注意使用for循环函数和求和函数时的不同matlab命令,避免混淆出错。使用函数trapz(),quad()是要注意被积函数是数值形式,应使用数组计算,应用点除否则将出错,不能调试出结果。
2、 使用函数trapz(),quad()和附录程序求解,均不能调试出获得正确答案。最后尝试用matlab命令中的符号求积分才得出正确结果。
3、 参照附录B中的求和函数程序设计顺利该变了附录A和C。发现使用求和函数时,inum不需要赋初值,应用了积分理论中分割、近似、求和
4、 取极限的思想方法,避免了for循环的冗杂性,较容易理解。
实验结果报告及实验总结
2、 结果:梯形法 inum=0.69315152080005
抛物线法 inum=0.69314718056936
使用函数trapz()
ans=0.69315152080005
使用函数quad()
Ans=0.69314719986297
将题中的近似计算结果相比较,发现运用不同的方法,计算结果会有不同。而梯形法误差较大,抛物线法急死计算定积分,接近于实际值,精确度高
3、 结果:只有使用matlab命令时才能计算出结果
I=1/2*pi
矩形法、梯形法、抛物线法是主要研究定积分的三种近似计算算法。trapz(),quad()也是用于定积分的近似数值计算。对于不定积分,由于积分区间无限大,故不能试过那个该分割方法
思考与深入:
通过本实验加深理解了积分理论中分割、近似、求和、取极限的思想方法。学习并掌握了用mablab求定积分的方法,了解了定积分近似计算的矩形法、梯形法和抛物线法。并认识到对于不同的题目,采取不同的运算方法,结果会不同,且精确度也不同。
同时,对于自身,要深刻理解不定积分、定积分概念,熟悉matllab数学软解的求不定积分
定积分的命令,了解简单的编程语句,以更快更准确且熟练的设计出程序。
教师评语
-
matlab实验报告
MATLAB教程及实训实验报告班级:10级专升本学号:姓名:实验1熟悉matlab的开发环境及矩阵操作一、实验的教学目标通过本次实…
-
matlab基本操作实验报告
实验一matlab基本操作一实验目的熟悉matlab的安装与启动熟悉matlab用户界面熟悉matlab功能建模元素熟悉matla…
-
matlab实验报告
课程设计说明书(论文)题目带限数字基带传输系统的仿真课程名称Matlab通信仿真设计专业通信工程班级1203学生姓名学号指导教师设…
-
matlab音乐处理合成实验报告
MATLAB高级编程与工程应用语音合成综合实验姓名班级学号日期121简单的合成音乐1请根据东方红片断的简谱和十二平均律计算出该片断…
-
东南大学几何与代数matlab实验报告
数学实验报告学号姓名吴雪松得分实验1求解线性方程组实验内容用MATLAB求解如下线性方程组Axb其中5100A0000651000…
- Matlab数学实验报告模板
-
matlab实验报告
MATLAB教程及实训实验报告班级:10级专升本学号:姓名:实验1熟悉matlab的开发环境及矩阵操作一、实验的教学目标通过本次实…
-
matlab实验报告
MATLAB实验报告实验一MATLAB语言平台与SIMULINK工具箱一目的与任务1学习了解MATLAB语言环境2练习MATLAB…
-
Matlab实验报告
程序设计训练报告题目学生姓名学生学号专业班级指导老师20xx年6月22日一实验名称用matlab处理基本运算与画图二实验目的1掌握…
-
Matlab实验报告三(画二维图形与三维曲面)
数学与信息科学系实验报告实验名称所属课程数学软件与实验实验类型综合型实验专业信息与计算科学班级学号姓名指导教师1234567
-
matlab实验心得总结
通过《matlab仿真》实验使我学习掌握了许多知识。首先是对matlab有了一个全新的认识,其次是对matlab的更多操作和命令的…