数学极限总结
数学极限总结
§2.1数列的极限
定义1 对于数列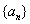 ,如果当
,如果当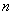 无限增大时,通项
无限增大时,通项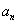 无限趋近于一个确定的常数A,则称A为数列
无限趋近于一个确定的常数A,则称A为数列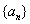 的极限,或称数列
的极限,或称数列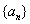 收敛于A,记作
收敛于A,记作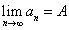 或
或 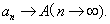
若数列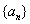 没有极限,则称该数列发散。
没有极限,则称该数列发散。
定义2(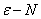 定义) 如果数列
定义) 如果数列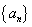 与常数A有下列关系:对于任意给定的正数
与常数A有下列关系:对于任意给定的正数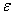 (无论它多么小)总存在正整数N,使得对于
(无论它多么小)总存在正整数N,使得对于 时的一切
时的一切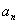 ,不等式
,不等式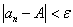 都成立,则称常数A是数列
都成立,则称常数A是数列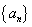 的极限。或称数列
的极限。或称数列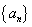 收敛于A,记为
收敛于A,记为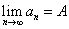 。
。
§2.2函数的极限
定义2(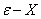 定义)如果对于任意给定的正数
定义)如果对于任意给定的正数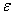 (不论它多么小),总存在着正数
(不论它多么小),总存在着正数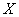 ,使得对于适合不等式
,使得对于适合不等式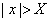 的一切
的一切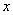 ,对应的函数值
,对应的函数值 都满足不等式
都满足不等式 ,那么常数
,那么常数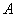 就叫做函数
就叫做函数 当
当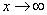 时的极限,记作
时的极限,记作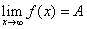 或
或 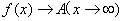 。
。
定义3(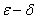 定义)如果对于任意给定的正数
定义)如果对于任意给定的正数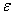 (不论它多么小),总存在着正数
(不论它多么小),总存在着正数 ,使得对于适合不等式
,使得对于适合不等式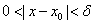 的一切
的一切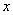 ,对应的函数值
,对应的函数值 都满足不等式
都满足不等式 ,那么常数
,那么常数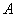 就叫做函数
就叫做函数 当
当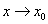 时的极限,记作
时的极限,记作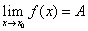 或
或 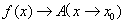 。
。
单侧极限
若函数 当自变量
当自变量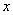 从
从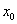 的左侧(右侧)无限趋近于
的左侧(右侧)无限趋近于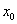 时,相应的函数值
时,相应的函数值 无限接近于一个确定的常数A,则称A为函数
无限接近于一个确定的常数A,则称A为函数 在
在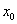 处的左(右)极限,记作
处的左(右)极限,记作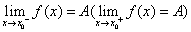 ,或
,或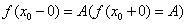 。
。
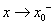 表示
表示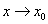 且
且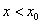 ;
;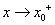 表示
表示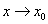 且
且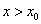 。
。
定理 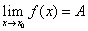 的充要条件是
的充要条件是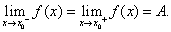
§2.3无穷小量与无穷大量
一.无穷小量
定义1 以零为极限的变量称为无穷小量,简称为无穷小。
注:(1)说一个变量是无穷小,要指明自变量的变化过程。
(2)无穷小是变量,表达的是量的变化趋势,而不是量的大小,因此,一个数不管多么小,都不是无穷小。
(3)零是唯一例外的常数中的无穷小。
2.无穷小的运算性质
定理1 有限个无穷小的代数和是无穷小。
注意,无穷多个无穷小的代数和不一定是无穷小。如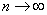 时,
时,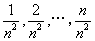 均为无穷小,但
均为无穷小,但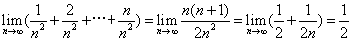
定理2 无穷小与有界量之积是无穷小。
推论1 常数与无穷小之积是无穷小。
推论2 有限个无穷小之积仍是无穷小。
二.无穷大量
定义2 若当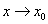 时,函数
时,函数 的绝对值
的绝对值 无限增大,则称
无限增大,则称 为当
为当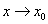 时的无穷大量,简称无穷大,记为
时的无穷大量,简称无穷大,记为 。
。
若当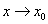 时,函数
时,函数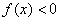 ,且绝对值
,且绝对值 无限增大,则称
无限增大,则称 为当
为当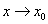 时的负无穷大量,记为
时的负无穷大量,记为 。
。
类似可以理解 ,
, ,
, ,
, 等表达式的意义。
等表达式的意义。
注:(1)说函数是无穷大,也要指明自变量的变化过程。
(2)无穷大也是变量,无论多么大的数都不是无穷大。
(3)无穷大必无界,但反之不真,例如, ,当
,当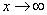 时是无界的,但不是无穷大。
时是无界的,但不是无穷大。
一、 无穷大与无穷小的关系
定理 在自变量的同一变化过程中,无穷大的倒数是无穷小,恒不为零的无穷小的倒数是无穷大。
定义设 是同一变化过程中的无穷小量,且
是同一变化过程中的无穷小量,且 :
:
若 ,称
,称 是比
是比 高阶的无穷小量,记作
高阶的无穷小量,记作 ;
;
若 ,称
,称 是比
是比 低阶的无穷小量;
低阶的无穷小量;
若 ,称
,称 与
与 是同阶无穷小量;
是同阶无穷小量;
特别地,当 时,称
时,称 与
与 是等价无穷小量,记作
是等价无穷小量,记作
若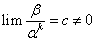
 ,称
,称 是关于
是关于 的
的 阶无穷小量。
阶无穷小量。
定理(等价无穷小的替换定理)若 ,且
,且 存在,则
存在,则 =
= 。
。
证: =
=

 。
。
§2.4极限的性质
一、 极限的性质
1.唯一性:若数列的极限存在,则极限值是唯一的,且其子数列的极限与原数列的相等;
2.有界性:如果一个数列收敛(有极限),那么这个数列有界。但是,如果一个数列有界,这个数列未必收敛。
3.保号性:如果一个数列{xn}收敛于a,且a>0(或a<0),那么存在正整数N,当n>N时,都有xn>0(或xn<0)。
4.改变数列的有限项,不改变数列的极限
二、 极限的四则运算
定理 如果 及
及 存在,并且
存在,并且 ,则
,则
法则(1)  存在,且
存在,且

法则(2)  存在,且
存在,且
 。
。
推论1  (C为任意常数)。
(C为任意常数)。
推论2  。
。
法则(3) 当 时,
时, 存在,且
存在,且
§2.5函数的极限性
定义 设函数 在点
在点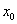 的某邻域有定义,如果
的某邻域有定义,如果 ,则称函数
,则称函数 在点
在点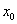 是连续的。
是连续的。
函数在一点连续,必须同时满足以下三个条件:
(1)函数 在点
在点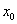 处有定义;
处有定义;
(2) 存在;
存在;
(3) 。
。
若以上条件有一个不满足,则称函数 在
在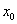 间断,
间断,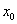 称为函数的间断点。
称为函数的间断点。
函数的间断点分为两类:左右极限都存在的间断点称为第一类间断点;左右极限至少有一个不存在的间断点称为第二类间断点。
初等函数的连续性
1. 基本初等函数在其定义域内连续;
2. 一切初等函数在其定义区间内连续。
闭区间上连续函数的性质
1最值性 闭区间上连续函数在该区间上一定取得最大值与最小值。
2 有界性 闭区间上的连续函数一定有界。
3介值性 闭区间上的连续函数,对介于最大、最小之间的任意常数,在该区间内至少有一点,使其函数值等于该常数。
4 零值定理常用于证明方程实根的存在性。
第二篇:高等数学B上册 求极限方法总结
求极限的几种常用方法
1.约去零因子求极限
例1:求极限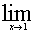
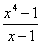

【说明】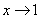 表明x与1无限接近,但
表明x与1无限接近,但 ,所以
,所以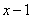 这一零因子可以约去。
这一零因子可以约去。
【解】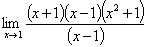 =
=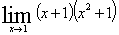 =4
=4
2.分子分母同除求极限
例2:求极限
【说明】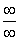 型且分子分母都以多项式给出的极限,可通过分子分母同除来求。 ?
型且分子分母都以多项式给出的极限,可通过分子分母同除来求。 ?
【解】
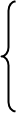 【注】(1)一般分子分母同除x的最高次方;
【注】(1)一般分子分母同除x的最高次方;
0 m>n
? (2)
 m<n
m<n
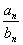 m=n
m=n
3.分子(母)有理化求极限
例3:求极限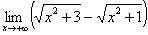 ??
??
【说明】分子或分母有理化求极限,是通过有理化化去无理式。
【解】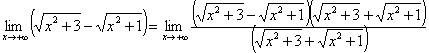
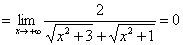
例4:求极限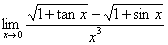
【解】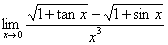 =
=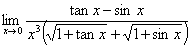
= =
=
【注】本题除了使用分子有理化方法外,及时分离极限式中的非零因子是解题的关键
4.应用两个重要极限求极限
两个重要的极限(1)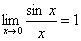
(2)
在这一类型题中,一般也不能直接运用公式,需要恒等变形进行化简后才可
以利用公式。
例5:求极限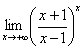
【说明】第二个重要极限主要搞清楚凑的步骤:先凑出1,再凑+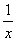 ,最后凑指数部分。
,最后凑指数部分。
【解】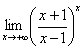 =
=

补:求下列函数的极限
(1)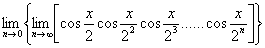
(2)(2)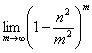
5.利用无穷小量的性质求极限
无穷小量的性质:无穷小量与有界量的乘积还是无穷小量。如果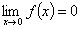 ,
,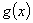 在某区间
在某区间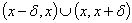 有界,则
有界,则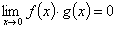 。这种方法可以处理一个函数不存在但有界,和另一个函数的极限是零的极限的乘积的问题。
。这种方法可以处理一个函数不存在但有界,和另一个函数的极限是零的极限的乘积的问题。
例6:求
【解】因为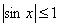
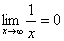
所以 =0
=0
6.用等价无穷小量代换求极限
【说明】
(1)常见等价无穷小有:
当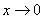 时,
时, ,
,
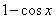 ~
~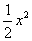 ,
,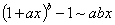
(2) 等价无穷小量代换,只能代换极限式中的因式。
(3) 此方法在各种求极限的方法中应作为首选。
例7:
【解】 
例8:求极限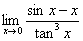 ?
?
【解】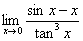 =
=
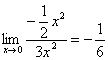
7.利用函数的连续性求极限
这种方法适合求复合函数的极限。如果 在点
在点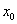 处连续
处连续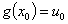 ,而
,而 在点
在点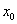 处连续,那么复合函数
处连续,那么复合函数 在点
在点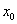 处连续。
处连续。 =
= =
=
 也就说,极限号
也就说,极限号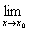 与
与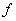 可以互换顺序。
可以互换顺序。
例9:求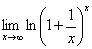
【解】令
因为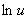 在点
在点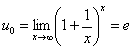 处连续
处连续
所以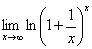
=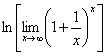
=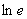
=1
8.用洛必达法则求极限
洛必达法则只能对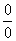 或
或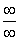 型才可直接使用,其他待定型必须先化成这两种类型之一,然后再应用洛必达法则。洛必达法则只说明当也存在
型才可直接使用,其他待定型必须先化成这两种类型之一,然后再应用洛必达法则。洛必达法则只说明当也存在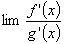 等于A时,那么
等于A时,那么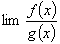 存在且等于A。如果
存在且等于A。如果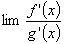 不存在时,并不能断定
不存在时,并不能断定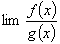 也不存在,这是不能用洛必达法则的,而须用其他方法讨论
也不存在,这是不能用洛必达法则的,而须用其他方法讨论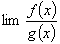 。
。
例10:求极限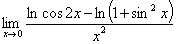
【解】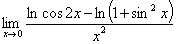
=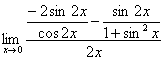
= ?
?
=3
9.用对数恒等式求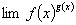 极限
极限
例11:求极限
【解】 =
=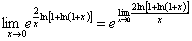 =
=
【注】对于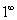 型未定义式,也可以用公式
型未定义式,也可以用公式
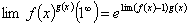
因为

10.利用两个准则求极限
(1)夹逼准则:若一正数N。当n>N时,有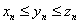 且
且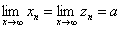 ,则有
,则有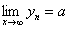 .
.
利用夹逼准则求极限关键在于从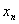 的表达式中,通常通过放大或缩小的方法找出两个有相同极限值的数列
的表达式中,通常通过放大或缩小的方法找出两个有相同极限值的数列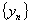 和
和 ,使得
,使得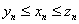 。
。
例12:
求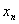 的极限。
的极限。
【解】因为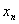 单调递减,所以存在最大项和最小项
单调递减,所以存在最大项和最小项
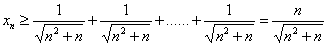

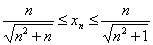
又因为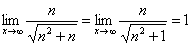
所以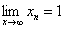
(2)单调有界准则:单调有界数列必有极限,而且极限唯一。
利用单调有界准则求极限,关键先要证明数列的存在,然后根据数列的
通项递推公式求极限。
例,证明下列极限存在,并求其极限。
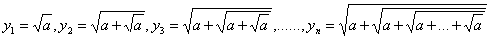
证明:从这个数列看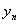 显然是增加的。用归纳法可证。
显然是增加的。用归纳法可证。
又因为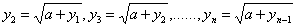
所以得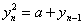 .因为前面证明
.因为前面证明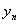 是单调增加的。
是单调增加的。
两端除以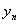 得
得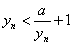
因为 则
则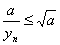 ,从而
,从而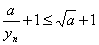
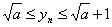
即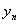 是有界的。根据定理
是有界的。根据定理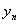 有极限且极限唯一。
有极限且极限唯一。
令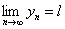 则
则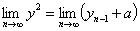
则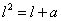 ,因为
,因为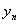 >0.解方程得
>0.解方程得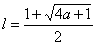
所以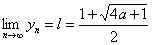
本文对极限的求法作了一下小结归纳了几种求极限的基本方法。对一般的极限用上面的方法可以求出来,复杂一点的可能要综合几种方法才能求出,关键是“运用之妙,存孚一心”。
-
数学极限总结
数学极限总结21数列的极限定义1对于数列an如果当n无限增大时通项an无限趋近于一个确定的常数A则称A为数列an的极限或称数列an…
-
极限的总结
极限的总结如下极限的保号性很重要就是说在一定区间内函数的正负与极限一致1极限分为一般极限还有个数列极限区别在于数列极限时发散的是一…
-
极限计算方法总结
电力电子科学与技术101班高等数学论文极限方法总结20xx10107刘帅20xx10110孙力铎20xx52920xx10113张…
-
极限计算方法总结
极限计算方法总结靳一东高等数学是理工科院校最重要的基础课之一极限是高等数学的重要组成部分求极限方法众多非常灵活给函授学员的学习带来…
-
极限计算总结
极限计算方法总结数学是专接本公共课重要的基础课之一极限是数学的重要组成部分求极限方法众多非常灵活给函授学员的学习带来较大困难而极限…
-
大学数学函数与极限的学习总结
好多大学生都以为上了大学就轻松啦,甚至以为没了数学,但是往往结果和想象的不一样,大学高等数学,就好像一个拦路虎,阻挡了去路。那么,…
-
高数:总结求极限的常用方法
总结求极限的常用方法,详细列举,至少4种极限定义法泰勒展开法。洛必达法则。等价无穷小和等价无穷大。极限的求法1.直接代入法适用于分…
-
常用求极限方法的探索与总结
论文题目:————————学院:——————————专业班级:——————————姓名:——————————学号:——————常用…
-
关于高数极限的几点总结
关于高数极限的几点总结首先说下我的感觉,假如高等数学是棵树木得话,那么极限就是他的根,函数就是他的皮。树没有跟,活不下去,没有皮,…
- 分析选讲知识小结10 多元函数的极限与连续
-
求极限的方法总结
求数列极限的方法总结摘要数列极限的求法一直是数列中一个比较重要的问题,本文通过归纳和总结,从不同的方面罗列了它的几种求法。关键词数…