数学实验“线性多步法(数值积分法,Taylor展开法)”实验报告(内含matlab程序)
西京学院数学软件实验任务书

实验二十五实验报告
一、实验名称:线性多步法(数值积分法,Taylor展开法)。
二、实验目的:进一步熟悉线性多步法(数值积分法,Taylor展开法)。
三、实验要求:运用Matlab/C/C++/Java/Maple/Mathematica等其中一种语言完成程序设计。
四、实验原理:
1.数值积分法:
常微分方程初值问题
 (1)
(1)
数值解法中,某一步的公式不仅与前一步解的值有关,而且与前若干步解的值有关,利用前面多步的信息预测下一步的值,这就是多步法的基本思想,可以期望获得较高的精度。
将(1)中的方程在区间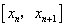 上积分,可以得到:
上积分,可以得到:

用等距节点的插值多项式来替代被积函数,再对插值多项式积分,这样就得到一系列求积公式。
用梯形方法计算积分项
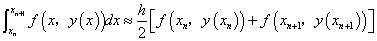
代入(1)中得:

设由 个数据点
个数据点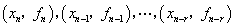 构造插值多项式
构造插值多项式 ,这里
,这里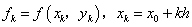 ,运用插值公式有:
,运用插值公式有:
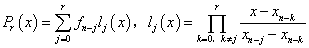
得到下列计算公式:
 (2)
(2)
其中,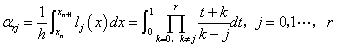
由此可得(2)中的系数。公式(2)是一个r+1步的显式公式,称为Adams显式公式。
2.Taylor展开法:
基于数值积分可以构造出一系列求解常微分方程的计算公式,下面介绍基于 Taylor 展开的待定系数法,它可灵活地构造出线性多步法。对固定的系数,可以选取待定系数使线性多步法的阶尽可能高。还可以根据需要,确定显式还是隐式。
设构造如下具有 p 阶精度的线性多步公式:
 (4)
(4)
它们的局部截断误差为:
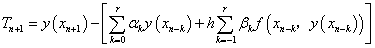
即: (5)
(5)
对(5)式的右端各项在 点处作Taylor展开有:
点处作Taylor展开有:

代入(5)中得:

使 的系数为零,得到关于
的系数为零,得到关于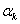 和
和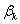 的线性方程组:
的线性方程组:
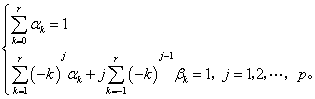
而且得到线性多步法的局部截断误差:
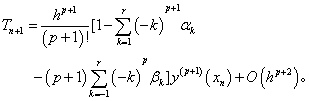
五、实验内容:
%数值积分法
function [k,X,Y,wucha,P]= Adams4x(funfcn,x0,b,y0,h)
x=x0; y=y0;p=128; n=fix((b-x0)/h);
if n<5
return;
end
X=zeros(p,1);
Y=zeros(p,length(y)); f=zeros(p,1);
k=1; X(k)=x; Y(k,:)=y';
for k=2:4
c1=1/6;c2=2/6;c3=2/6;
c4=1/6;a2=1/2; a3=1/2;
a4=1;b21=1/2;b31=0;
b32=1/2; b41=0;b42=0;b43=1;
x1=x+a2*h; x2=x+a3*h;
x3=x+a4*h; k1=feval(funfcn,x,y);
y1=y+b21*h*k1; x=x+h;
k2=feval(funfcn,x1,y1);
y2=y+b31*h*k1+b32*h*k2;
k3=feval(funfcn,x2,y2);
y3=y+b41*h*k1+b42*h*k2+b43*h*k3;
k4=feval(funfcn,x3,y3);
y=y+h*(c1*k1+c2*k2+c3*k3+c4*k4); X(k)=x; Y(k,:)=y;
end
X;Y;f(1:4)=feval(funfcn,X(1:4),Y(1:4));
for k=4:n
f(k)=feval(funfcn,X(k),Y(k));
X(k+1)=X(1)+h*k;
Y(k+1)=Y(k)+(h/24)*((f(k-3:k))'*[-9 37 -59 55]');
f(k+1)= feval(funfcn,X(k+1),Y(k+1));f(k)=f(k+1); k=k+1;
end
for k=2:n+1
wucha(k)=norm(Y(k)-Y(k-1)); k=k+1;
end
X=X(1:n+1); Y=Y(1:n+1,:); n=1:n+1,
wucha=wucha(1:n,:); P=[n',X,Y,wucha'];
第二篇:数学实验“线性方程组的最速下降法与共轭梯度法解法”实验报告(内含matlab程序代码)
西京学院数学软件实验任务书

实验五实验报告
一、实验名称:最速下降法与共轭梯度法解线性方程组。
二、实验目的:进一步熟悉理解掌握最速下降法与共轭梯度法解法思路,提高matlab编程能力。
三、实验要求:已知线性方程矩阵,应用最速下降与共轭梯度法在相关软件编程求解线性方程组的解。
四、实验原理:
1.最速下降法:
从某个初始点 出发,沿
出发,沿 在点
在点 处的负梯度方向
处的负梯度方向

求得 的极小值点
的极小值点 , 即
, 即

然后从 出发,重复上面的过程得到
出发,重复上面的过程得到 。如此下去,得到序列{
。如此下去,得到序列{ }
}
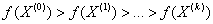
可以证明,从任一初始点 出发, 用最速下降法所得到的序列{
出发, 用最速下降法所得到的序列{ }均收敛于问题使
}均收敛于问题使 最小化
最小化 的解,也就是方程组
的解,也就是方程组 的解。其收敛速度取决于
的解。其收敛速度取决于 ,其中
,其中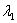 ,
,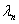 分别为A的最小,最大特征值。最速下降法迭代格式:给定初值
分别为A的最小,最大特征值。最速下降法迭代格式:给定初值 ,
, 按如下方法决定:
按如下方法决定:

2.共轭梯度法
其基本步骤是在点 处选取搜索方向
处选取搜索方向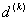 , 使其与前一次的搜索方向
, 使其与前一次的搜索方向 关于
关于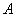 共轭,即
共轭,即
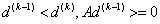
然后从点 出发,沿方向
出发,沿方向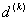 求得
求得 的极小值点
的极小值点 , 即
, 即

如此下去, 得到序列{ }。不难求得
}。不难求得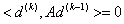 的解为
的解为
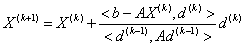
注意到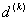 的选取不唯一,我们可取
的选取不唯一,我们可取

由共轭的定义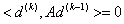 可得:
可得:
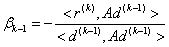
共轭梯度法的计算过程如下:
第一步:取初始向量 , 计算
, 计算

第 步:计算
步:计算

五、实验内容:
%最速下降法
function [x,k]=fastest(A,b,eps);
x0=zeros(size(b),1);
x=x0;
k=0;
m=1000;
tol=1;
while tol>=eps
r=b-A*x0;
q=dot(r,r)/dot(A*r,r);
x=x0+q*r;
k=k+1;
tol=norm(x-x0);
x0=x;
if k>=m
disp('迭代次数太多,可能不收敛!');
return;
end
end
x
k
%共轭梯度法
function [k,x]=gong_e(A,b)
esp=input('请输入允许误差esp=');
x0=input('请输入初始值x0=');
k = 0 ;
r0 = b-A*x0; %求出dangqian梯度
while norm(r0)>esp
r0 = b -A*x0;
k = k + 1 ;
if k==1
p0 = r0 ;
else
lamda=(r0'*r0)/(p0'*A*p0);
r1 = r0 - lamda*A*p0 ;
p0=r0+(r0'*r0)/(r1'*r1)*p0;
x1 = x0 + lamda*p0;
x0=x1;
r0=r1;
end
end
x=r0;
k;
end
六、实验结果:
A=[5 2 0;6 4 1;1 2 5];
b=[10 18 -14]';
eps=1.0e-6;
x =
-0.8750
7.1875
-5.5000
k =
60
-
《数学实验》报告matlab_第六次作业
数学实验报告实验名称matlab常微分概率和统计作图学院机械工程学院专业班级姓名学号20xx年11月一实验目的掌握运用Matlab…
- Matlab数学实验报告模板
-
《数学实验》报告matlab-_第三次作业
数学实验报告实验名称matlab绘图学院机械工程学院20xx年10月一实验目的掌握Matlab绘图的基本知识学会使用matlab绘…
-
matlab数学实验报告2
西安交通大学数学实验报告数学实验报告20xx年6月12日2西安交通大学数学实验报告培养容器温度变化率模型一实验目的利用matlab…
-
matlab——大学数学实验报告
济南大学20##~20##学年第二学期数学实验上机考试题班级计科1201学号##姓名##考试时间20##年6月17日授课教师##说…
-
mathematica数学实验报告实验四
数学实验报告实验四学院数学与统计学院班级信息与计算科学1班姓名郝玉霞学号20xx71020xx7实验四一实验名称数列与级数二实验目…
- 数学应用软件实验报告(mathematica实验程序)3
- mathematica数学实验报告
-
Mathematica实验报告
Mathematica实验报告实验名称利用MATHEMATICA作图运算及编程实验目的1掌握用MATHEMATICA作二维图形熟练…
-
mathematica数学实验报告 实验二
数学实验报告实验二学院:数学与统计学院班级:信息与计算科学(1)班姓名:学号:实验二一、实验名称:的计算二、实验目的:首先在Mat…
- Matlab数学实验报告模板