mathematica数学实验报告 实验二
数 学 实 验 报 告
实验二
学院:数学与统计学院
班级:信息与计算科学(1)班
姓名:
学号:
实验二
一、实验名称:π的计算
二、实验目的:首先在Mathematica环境中用多种方法计算圆周率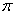 的值,通过实验来体会各种方法的区别,比较各种方法的优劣,接着尝试自己提出新的方法来计算圆周率
的值,通过实验来体会各种方法的区别,比较各种方法的优劣,接着尝试自己提出新的方法来计算圆周率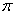 的值。
的值。
三、实验环境:学校机房,Mathematica软件。
四、实验的基本理论和方法
1、用Mathematica绘图函数Plot绘制圆周率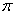 ;
;
2、计算圆周率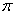 的数值积分法、泰勒级数法、蒙特卡罗法,并且利用特定的公式来计算圆周率
的数值积分法、泰勒级数法、蒙特卡罗法,并且利用特定的公式来计算圆周率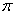 。
。
五、实验的内容和步骤及实验的结果和结果分析
步骤一、数值积分法计算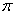
因为单位圆的半径为1,它的面积等于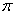 ,所以只要计算出单位圆的面积,就算出了
,所以只要计算出单位圆的面积,就算出了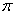 。在坐标轴上画出以圆点为圆心,以1为半径的单位圆,则这个单位圆在第一象限的部分是一个扇形,而且面积是单位圆的1/4,于是,我们只要算出此扇形的面积,便可以计算出
。在坐标轴上画出以圆点为圆心,以1为半径的单位圆,则这个单位圆在第一象限的部分是一个扇形,而且面积是单位圆的1/4,于是,我们只要算出此扇形的面积,便可以计算出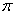 。
。
当n=5000时;
语句:
n=5000;y[x_]:=4/(1+x*x);
s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;
s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n);
Print[{N[s1,20],N[s2,30],N[Pi,30]}];
实验结果:
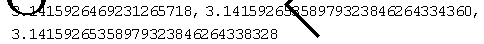
当n=10000时;
语句:
n=10000;y[x_]:=4/(1+x*x);
s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;
s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n);
Print[{N[s1,20],N[s2,30],N[Pi,30]}];
Plot[{4(1-x*x)},{x,0,1}]
实验结果:
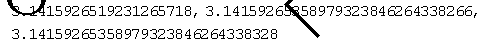
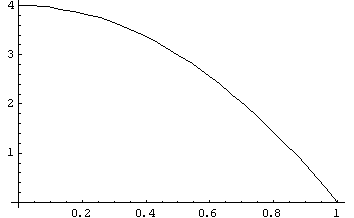
图1 1/4个单位圆
结果分析:当数值积分法得到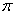 的近似值为3.14159265358979323846264338328,
的近似值为3.14159265358979323846264338328,
可以看出,用这种方法计算所得到的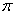 值是相当精确的,n越大,计算出来的扇形面积的近似值就越接近
值是相当精确的,n越大,计算出来的扇形面积的近似值就越接近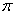 的准确值。
的准确值。
步骤二、泰勒级数法计算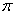
利用反正切函数的泰勒级数
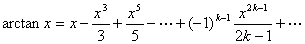
来计算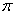 。
。
语句:T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}];
N[4*T[1,20000],20]//Timing
T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}];
Print[N[4*(T[1/2,260]+T[1/3,170]),150]];
Print[N[16*(T[1/5,110]-4*T[1/239,30]),150]];
Print[N[Pi,150]]
实验结果:

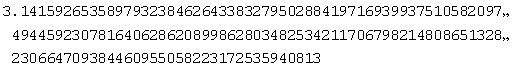
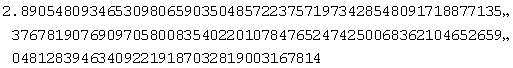
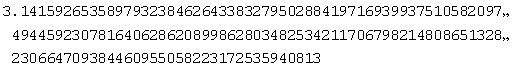
结果分析:从实验过程可以看出,这种方法花费的时间很长。原因是当x=1时得到的 的展开式收敛太慢。要使泰勒级数收敛得快,容易想到,应当使x的绝对值小于1,最好是远比1小。例如,因为
的展开式收敛太慢。要使泰勒级数收敛得快,容易想到,应当使x的绝对值小于1,最好是远比1小。例如,因为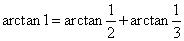 ,所以我们可以计算出
,所以我们可以计算出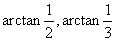 的值,从而得到
的值,从而得到 的值。这样,就使得收敛速度加快。改进后可以看出,泰勒级数法得到的结果比数值分析法精确到小数点后更多位。
的值。这样,就使得收敛速度加快。改进后可以看出,泰勒级数法得到的结果比数值分析法精确到小数点后更多位。
步骤三、蒙特卡罗法计算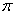
在数值分析法中,我们利用求单位圆的1/4面积来得到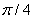 ,从而得到
,从而得到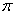 。单位圆的1/4是一个扇形,它是边长为1的单位正方形的一部分,单位正方形的面积
。单位圆的1/4是一个扇形,它是边长为1的单位正方形的一部分,单位正方形的面积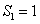 。只要能够求出扇形的面积
。只要能够求出扇形的面积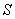 在正方形的面积中所占的比例
在正方形的面积中所占的比例 ,就能立即得到
,就能立即得到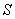 ,从而得到
,从而得到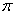 的值。下面的问题归结为如何求
的值。下面的问题归结为如何求 的值,这就用到了一种利用随机数来解决此种问题的蒙特卡罗法,其原理就是在正方形中随机的投入很多点,是所投的每个点落在正方形中每一个位置的机会均等,看其中有多少个点落在扇形内。降落在扇形内的点的个数
的值,这就用到了一种利用随机数来解决此种问题的蒙特卡罗法,其原理就是在正方形中随机的投入很多点,是所投的每个点落在正方形中每一个位置的机会均等,看其中有多少个点落在扇形内。降落在扇形内的点的个数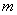 与所投店的总数
与所投店的总数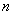 的比可以近似的作为
的比可以近似的作为 的近似值。
的近似值。
语句:
n=10000;p={};
Do[m=0;
Do[x=Random[];y=Random[];
If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10
实验结果:
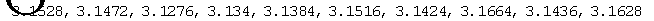
3.14668
结果分析:
从运行结果来看,蒙特卡罗法的计算结果为3.14668,虽然精确度不太高,但运行时间短,在很多场合下,特别是在对精确度要求不高的情况下很有用的。
步骤四、针对步骤三提出疑问:步骤三中我们发现当n=10000时,蒙特卡罗法的计算结果为3.14668,精确度不太高,那么对n取不同的值,所得结果的精确度会不会有变化?假如有变化,会有什么变化呢?
猜想:对n取不同的值,所得结果的精确度应该会有变化,且当n值越大,所得结果越精确。
现令n=1000;
语句:
n=1000;p={};
Do[m=0;
Do[x=Random[];y=Random[];
If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10
实验结果:
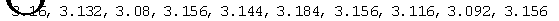
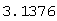
令n=100000;
语句:
n=100000;p={};
Do[m=0;
Do[x=Random[];y=Random[];
If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10
实验结果:
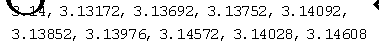
结果分析:
从运行结果来看,虽然蒙特卡罗法的计算结果的精确度不太高,但对n取不同的值,所得结果的精确度有变化,且当n值越大,所得结果越精确,这与我们的猜想完全一致。
步骤五、利用麦琴给出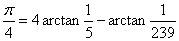 ,推出π=4(
,推出π=4(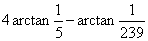 )。对比以上方法,这种简单的直接用公式求的π的方法要简单得多,所以用处更广。
)。对比以上方法,这种简单的直接用公式求的π的方法要简单得多,所以用处更广。
第二篇:《数学实验报告》样例
数学实验报告
实验序号:1 日期:20##年6月18 日星期五

-
Mathematica实验报告
Mathematica实验报告实验名称利用MATHEMATICA作图运算及编程实验目的1掌握用MATHEMATICA作二维图形熟练…
- mathematica数学实验报告
-
mathematica数学实验报告 实验二
数学实验报告实验二学院:数学与统计学院班级:信息与计算科学(1)班姓名:学号:实验二一、实验名称:的计算二、实验目的:首先在Mat…
-
mathematica数学实验报告
高等数学实验报告实验一一、实验题目1:作出各种标准二次曲面的图形2:作出曲面所围的图形二、实验目的和意义方法的理论意义和实用价值。…
- 实验一 微积分基础 mathmatic数学实验报告 王文翰实验1
-
mathematica数学实验报告实验四
数学实验报告实验四学院数学与统计学院班级信息与计算科学1班姓名郝玉霞学号20xx71020xx7实验四一实验名称数列与级数二实验目…
- 数学应用软件实验报告(mathematica实验程序)3
- mathematica数学实验报告
-
数学实验“线性多步法(数值积分法,Taylor展开法)”实验报告(内含matlab程序)
西京学院数学软件实验任务书实验二十五实验报告一实验名称线性多步法数值积分法Taylor展开法二实验目的进一步熟悉线性多步法数值积分…
-
Mathematica实验报告
Mathematica实验报告实验名称利用MATHEMATICA作图运算及编程实验目的1掌握用MATHEMATICA作二维图形熟练…
-
Mathematica课程设计
数学实验综合实验学院数学与统计学院专业学生姓名学号20xx71020xx5实验目的1使我们掌握可以用来做数学的工具Mathemat…