教学设计

 

第二篇：教学设计与反思1-《用函数观点看一元二次方程》教学设计与教学反思

《用函数观点看一元二次方程》教学设计与教学反思（初中数学九年级）

一、学情分析：

大部分学生上课能够积极发言，认真完成作业，学习态度端正，但缺乏一定的学习方法，也缺少学习毅力，在某种程度上还是不能够严格要求自己。

二、教学内容分析：

1、教学目标

①知识与技能：总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，表述何时方程有两个不等的实根、两个相等的实数和没有实根；会利用二次函数的图象求一元二次方程的近似解。

②过程与方法：经历探索二次函数与一元二次方程的关系的过程，体会方程与函数之间的联系。

③情感态度价值观：通过观察二次函数图象与x轴的交点个数，讨论一元二次方程的根的情况，进一步体会数形结合思想。

2、重点、难点分析：

①重点：方程与函数之间的联系，会利用二次函数的图象求一元二次方程的近似解。

②难点：二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系。

三、教学过程设计：

（一）创设情境、导入新课

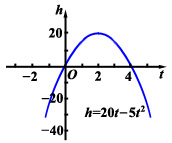
问题1  如图，以 40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线。如果不考虑空气阻力，球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有关系h＝20t-5t²。

考虑以下问题

（1）球的飞行高度能否达到 15m？如能，需要多少飞行时间？

（2）球的飞行高度能否达到 20m？如能，需要多少飞行时间？

（3）球的飞行高度能否达到 20.5m？为什么？

（4）球从飞出到落地要用多少时间？

 

分析：由于球的飞行高度h与飞行时间t的关系是二次函数h=20t-5t²。

所以可以将问题中h的值代入函数解析式，得到关于t的一元二次方程，如果方程有合乎实际的解，则说明球的飞行高度可以达到问题中h的值；否则，说明球的飞行高度不能达到问题中h的值。

解：（1）解方程 15＝20t-5t²。 

　　t²-4t+3=0。 

　　t₁＝1，t₂＝3。

　　当球飞行1s和3s时，它的高度为 15m。

分析：由于球的飞行高度h与飞行时间t的关系是二次函数h=20t-5t²。

所以可以将问题中h的值代入函数解析式，得到关于t的一元二次方程，如果方程有合乎实际的解，则说明球的飞行高度可以达到问题中h的值；否则，说明球的飞行高度不能达到问题中h的值。

　　

解：（1）解方程 15＝20t-5t²。 

　　t²-4t+3=0。 

　　t₁＝1，t₂＝3。

　　答：当球飞行1s和3s时，它的高度为 15m。

  (2)解方程 20＝20t-5t²。 

　　t²-4t+4＝0。 

　　t₁＝t₂＝2。

　　答：当球飞行2s时，它的高度为 20m。

　　（3）解方程 20.5＝20t-5t²。 

　　t²-4t+4.1＝0。

　　因为(－4)²－4×4.1<0。所以方程无解。

　　答：球的飞行高度达不到 20.5m。

　　（4）解方程  0＝20t-5t²。 

　　t²-4t＝0。 

　　t₁＝0，t₂＝4。

答：当球飞行0s和4s时，它的高度为 0m，即0s时球从地面飞出。4s时球落回地面。

画出二次函数h=20t-5t²的图象，观察图象，体会以上问题的答案。

从上面可以看出。二次函数与一元二次方程关系密切。

由学生小组讨论，总结出二次函数与一元二次方程的解有什么关系？

例如：已知二次函数y＝-x2+4x的值为3，求自变量x的值。可以解一元二次方程-x²+4x＝3(即x2-4x+3＝0)。反过来，解方程x²-4x+3＝0又可以看作已知二次函数y＝x²-4x+3的值为0，求自变量x的值。

一般地，我们可以利用二次函数y＝ax²+bx+c深入讨论一元二次方程ax²+bx+c＝0。

（二）尝试练习、互助纠错

1、二次函数(1)y＝x²+x-2；(2) y＝x²-6x+9；(3) y＝x²-x+1的图象如下图所示

  

（1）以上二次函数的图象与x轴有公共点吗？如果有，公共点的横坐标是多少？

（2）当x取公共点的横坐标时，函数的值是多少？由此，你能得出相应的一元二次方程的根吗？

 先画出以上二次函数的图象，由图象学生展开讨论，在老师的引导下回答以上的问题

从上面可以看出，二次函数与一元二次方程关系密切。

由学生小组讨论，总结出二次函数与一元二次方程的解有什么关系？

例如：已知二次函数y＝-x²+4x的值为3，求自变量x的值。可以解一元二次方程-x²+4x＝3(即x²-4x+3＝0)。反过来，解方程x²-4x+3＝0又可以看作已知二次函数y＝x²-4x+3的值为0，求自变量x的值。

一般地，我们可以利用二次函数y＝ax²+bx+c深入讨论一元二次方程ax²+bx+c＝0。

2、二次函数(1)y＝x²+x-2；(2) y＝x²-6x+9；(3) y＝x²-x+1的图象如下图所示

（1）以上二次函数的图象与x轴有公共点吗？如果有，公共点的横坐标是多少？

（2）当x取公共点的横坐标时，函数的值是多少？由此，你能得出相应的一元二次方程的根吗？

先画出以上二次函数的图象，由图象学生展开讨论，在老师的引导下回答以上的问题。可以看出：

（1）抛物线y＝x²+x-2与x轴有两个公共点，它们的横坐标是-2，1；当x取公共点的横坐标时，函数的值是0。由此得出方程x²+x-2 = 0的根是-2，1。

（2）抛物线y＝x²-6x+9与x轴有一个公共点，这点的横坐标是3。当x＝3时，函数的值是0。由此得出方程x²-6x+9=0有两个相等的实数根3。

（3）抛物线y＝x²-x+1与x轴没有公共点， 由此可知，方程x²-x+1 = 0没有实数根。

总结：一般地，如果二次函数y = ax²+bx+c的图像与x轴相交，那么交点的横坐标就是一元二次方程ax²+bx+c=0的根。

（三）归纳总结

一般地，从二次函数y＝ax²+bx+c的图象可知，

（1）如果抛物线y＝ax²＋bx＋c与x轴有公共点，公共点的横坐标是x₀，那么当x＝x₀时，函数的值是0，因此x＝x₀就是方程ax²＋bx＋c＝0的一个根。

（2）二次函数的图象与x轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点。这对应着一元二次方程根的三种情况：没有实数根，有两个相等的实数根，有两个不等的实数根。

由上面的结论，我们可以利用二次函数的图象求一元二次方程的根。由于作图或观察可能存在误差，由图象求得的根，一般是近似的。

四、教学反思：

让学生体验函数y＝x²和y＝bx＋c的交点的横坐标是方程x²＝bx＋c的解的探索过程，掌握用函数y＝x²和y＝bx＋c图象交点的方法求方程ax²＝bx＋c的解。通过渗透数形结合的思想，提高学生综合解题能力。