因式分解方法总结
因式分解
Y1、讲故事:
下定义:把一个多项式化成几个整式的乘积的形式,这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
(八年级上册第194页)
分解的对象:多项式
问题1:什么是多项式?
研究多项式的常规角度有哪些?
分解的结果:[整式] 单项式、多项式
[运算] 乘法
问题2:什么是整式?
问题3:分解的结果中,能不能都是单项式?为什么?
问题4:分解的结果中,能不能有两个或两个以上的单项式?为什么?
问题5:分解的结果中,能不能全是多项式?
Y2、结构
构成:
本质:[等式] 等号左边的多项式=等号右边的不能再因式分解的几个整式的乘积
[方程的解] 方程中未知数的解为全体实数
重要的组成部分:分解结果中至少含有一个多项式;有且仅有一个单项式。
部分与整体的联系:分解结果中的单项式是分解对象多项式各项的公因式。
Y3、分类
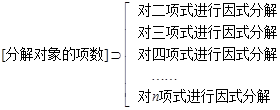


Y4、条件、特征
1、一元二次三项式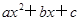 能在实数范围内因式分解的条件:
能在实数范围内因式分解的条件: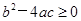
证明: ∵ 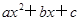 (配方法)
(配方法)
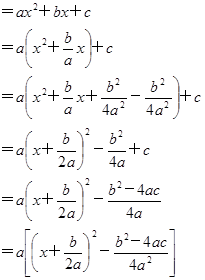
∴ 当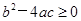 时:
时:
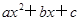
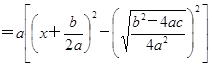
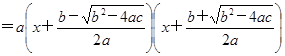
2、因式分解的方法
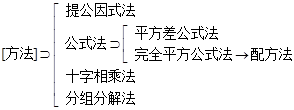
3、如何提取公因式
① 多项式的各项都有一个公共的因式。公因式可以是单项式,也可以是多项式。
② 如何提取单项式公因式(八年级上册第195页例1的分析)
[系数] [系数符号] 提公因式后保证多项式的最高次项的系数为正数。
[系数绝对值] 各项系数绝对值的最大公因数
[字母] 多项式各项公有的字母
[指数] 取公有字母的较小指数
③ 如何提取多项式公因式(引出“分组分解法”)
4、能够用平方差公式法进行因式分解的多项式的特征(八年级上册第196页“思考”下面的一段)
[项数] 两项
[系数符号] 两项的符号不同
[系数绝对值] 某实数的平方
[次数] 提取公因式后,每个字母、多项式的指数都是偶数
[常数项] 某实数的平方
5、能够用完全平方公式法进行因式分解的多项式的特征(八年级上册第198页“思考”下面的一段)
[项数] 三项
[降幂排列] 按同一字母进行降幂排列
[系数的符号] +++、———、+—+、—+—(降幂排列后首尾符号相同)
[系数绝对值] 中间项系数的绝对值是首尾项系数绝对值算术平方根的2倍
[指数] 首尾两项每个字母的指数都是偶数
同一字母,中间项的指数是首尾项指数的一半。
6、因式分解的步骤:
① 有提公因式的先提公因式,保证多项式的最高次项的系数为正数。
② 降幂排列。
③ 运用公式、分组等方法。
Y5、性质、应用
1、在实数的运算中的应用
① 提公因数法:

② 平方差公式法:
③ 模型:两个十位数字相同、个位数字之和为10的两位数相乘;积的末两位数等于这两个两位数的个位数字之积,末两位前的数字组成的数等于十位数乘以比它大1的数的积。
例:21×29=609 34×36=1224 58×52=3016 45×45=2025
证明:

 :表示个位数的乘积;
:表示个位数的乘积;
 :表示十位数乘以比它大1的数的积的100倍。
:表示十位数乘以比它大1的数的积的100倍。
2、在代数式求值(max、min)中的应用
① 已知 满足
满足 ,求
,求 的值。
的值。
② 求 的值,其中
的值,其中 ,
,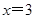 。
。
③ 若 ,求
,求 的值。
的值。
④ 已知 ,求
,求 。
。
⑤ 当 =______时,
=______时, 的值最大,这个最大值是______。
的值最大,这个最大值是______。
一元二次三项式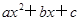 (
( )的最值模型:
)的最值模型:
当 ,
,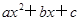 有最小值
有最小值
 时,
时,
当 ,
,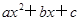 有最大值
有最大值
 时,
时,
证明:∵ 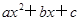
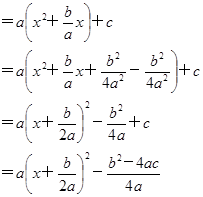
∴ 若 ,
, ,此时
,此时 。
。
若 ,
, ,此时
,此时 。
。
3、在解一元二次方程中的应用(用因式分解法解一元二次方程)
①  ②
②  0 ③
0 ③ 
④  ⑤
⑤ 
⑥  ⑦
⑦ 
4、在解一元二次不等式中的应用(用因式分解法解一元二次不等式)
① 
5、在化简二次根式中的应用
① 已知 ,则化简
,则化简 的结果是__________。
的结果是__________。
② 已知 ,求
,求 的值
的值
③ 当 时,化简
时,化简 __________。
__________。
④ 已知 ,化简
,化简 __________。
__________。
⑤ 化简 __________。
__________。
6、在非负式求值中的应用
① 已知: ,则
,则 __________。
__________。
② 若已知 ,化简
,化简 __________。
__________。
7、在分式的约分、通分、乘除法中的应用
①  ②
②  ③
③ 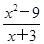 ④
④ 
⑤  ⑥
⑥ 
⑦ 
Y6、重要上位:式子变形
重要下位:[因式分解的方法] 用提公因式法的因式分解、用公式法的因式分解 ……。
Y7、角度、模型
Y8、诲人不倦
第二篇:因式分解方法总结
赏析因式分解中的奇方妙法
因式分解常见的重要方法有:①提公因式法;②运用公式法;③分组分解法。但是,对于一些繁杂的多项式,倘若仅用这些方法则难以奏效。下面本文结合例题介绍六种因式分解的新颖方法,供同学们学习时使用。
方法一:十字相乘法
即将二次三项式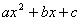 的系数
的系数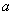 分解成
分解成 ,常数项
,常数项 分解成
分解成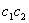 ,并且把
,并且把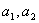 ,
,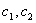 排列如下:
排列如下: ×
× ,这里按斜线交叉相乘,再相加得到
,这里按斜线交叉相乘,再相加得到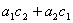 ,如果它正好等于
,如果它正好等于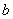 ,那么
,那么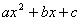 就可以分解成
就可以分解成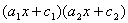
例1:分解因式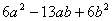
解:如右图所示: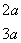 ×
×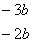 由十字相乘法得,原式=
由十字相乘法得,原式=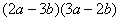
评注:利用十字相乘法分解因式的关键是把二次三项式中一次项系数和常数项分解因式,使得它们按斜线交叉相乘之积的和刚好等于原二次三项式中一次项的系数。
对应练习1:分解因式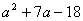
方法二:双十字相乘法
即对于某些二次六项式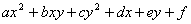 ,可以看做关于
,可以看做关于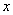 的二次三项式
的二次三项式
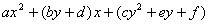 ,先用十字相乘法将常数项“
,先用十字相乘法将常数项“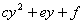 ”分解,再利用十字相乘法将关于
”分解,再利用十字相乘法将关于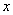 的二次三项式分解。
的二次三项式分解。
例2:分解因式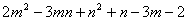
解:原式=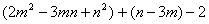
=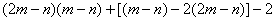
=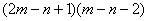
评注:运用双十字相乘法对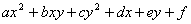 型的多项式分解因式的步骤如下:①用十字相乘法分解前三项组成的二次三项式;②在这个十字相乘图的右边再画一个“十”字,把常数项分解成两个因数,填在第二个十字的右端。使这两个因数在第二个十字交叉之积的和等于原式中含
型的多项式分解因式的步骤如下:①用十字相乘法分解前三项组成的二次三项式;②在这个十字相乘图的右边再画一个“十”字,把常数项分解成两个因数,填在第二个十字的右端。使这两个因数在第二个十字交叉之积的和等于原式中含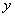 的一次项的系数
的一次项的系数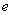 ,同时还必须与第一个十字左列的两个因数交叉相乘,使其交叉之积的和等于原式中含
,同时还必须与第一个十字左列的两个因数交叉相乘,使其交叉之积的和等于原式中含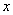 的一次项的系数
的一次项的系数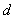
对应练习2:分解因式
方法三:整体换元法
即根据某复杂多项式的特征,把其中的某些部分看成一个整体,并用一个新的字母代替它,从而简化运算过程。但分解后要注意将新字母还原。
例3:分解因式
解:原式= =
=
令 ,则有
,则有
原式= =
= =
= =
=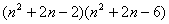
评注:运用整体换元法分解因式是将原多项式的某一部分用一个字母代替,使原多项式变成引入新变元(或新变元和原来变元混合)的多项式,从而使某些数量关系明朗化,进而便于分解因式。
对应练习3:分解因式
方法四:巧选主元法
即当题目中的某多项式所含的字母较多,问题较复杂时,我们可以把某一个字母作为主元,而将其它字母作为常数去解决问题。
例4:分解因式
解:把原式看作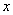 的二次三项式去分解,则有
的二次三项式去分解,则有
原式=
=
=
评注:当我们常见的字母作为主元难以分解时,不妨重选其它字母作主元,结合提公因式法、公式法和分组分解法等常见方法去分解因式,从而可以化难为易。
对应练习4:分解因式
方法五:活用配方法
即根据完全平方公式的形式和结合题设多项式的特点,将此多项式中的某一项拆成两项,或者在此多项式中添上两个符号相反绝对值相同的项,使得其可以化成完全平方公式或者平方差公式,从而简便分解因式。
例5:分解因式
解:原式=
=
=
=
= =
=
评注:配方法是一种特殊的添拆项法。如何拆项或添项的关键依赖于对题目所给代数式特点的观察和分析。
对应练习5:分解因式
方法六:待定系数法
即先假定一个含有待定系数的恒等式,然后根据各项恒等的性质,列出几个含有待确定系数的方程组,解之求得待定系数的值;或者从方程组中消去这些待定系数,求出原来那些已知系数间所存在的关系,从而解决问题。
例6:分解因式
解:因为 ,所以设原式=
,所以设原式=
即

 比较此等式两边对应项的系数得
比较此等式两边对应项的系数得  解得
解得 
故原式=
评注:利用待定系数法分解因式的数学思想是方程思想,其求解关键在利用相等多项式对应项系数相等的性质建立方程组,求出相关的待定系数的值。
对应练习6:分解因式
总之,对于因式分解题,只要我们仔细观察题设多项式的特点,合理灵活处理,这样新颖巧妙的分解因式的方法便应题而生。
对应练习题答案:
1原式=
2原式=
=
=
3设 ,则有
,则有
原式= =
=
= =
= =
=
= =
=
4把原式看作关于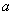 的二次三项式,则有
的二次三项式,则有
原式=
=
=
=
=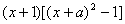
=
5原式=
=
=
=
=
=

 6因为
6因为 ,所以可设原式=
,所以可设原式= ,从而有
,从而有 ,由相等多项式对应项系数相等的性质得
,由相等多项式对应项系数相等的性质得  解得
解得 
故原式=
-
因式分解方法总结
因式分解Y1、讲故事:下定义:把一个多项式化成几个整式的乘积的形式,这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解…
-
因式分解总结及方法
因式分解方法技巧分解因式的常用方法:一提二用三查,即先考虑各项有无公因式可提;再考虑能否运用公式来分解;最后检查每个因式是否还可以…
-
因式分解的多种方法(初中版)
因式分解的方法初中版因式分解是初中一个重点它牵涉到分式方程一元二次方程所以很有必要学会一些基本的因式分解的方法下面列举了九种方法希…
-
因式分解所有方法归纳总结
因式分解的十二种方法:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解。因式分解的方法多种多样,现总结如下:1…
-
因式分解方法总结
因式分解方法总结一、定义定义:把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个多项式因式分解(也叫作分解因式).因式分…
-
农办半年工作总结
20xx年是十二五规划开官之年,我乡农业工作在党委、政府的高度重视下,认真贯彻落实县农村经济工作会议精神,注重粮食生产,探索经营机…
-
学雷锋演讲比赛总结讲话
老师们,同学们:大家好!今天下午,我校举办“学雷锋”为主题的演讲比赛,目的是号召全校师生以雷锋为榜样,进一步弘扬雷锋精神,立足自身…
-
银行面试题目总结
在做银行面试自我介绍的时候,往往有两种形式,一是口语自我介绍,一是书面作题。其实在做面试题的时候,一系列的解说都是对自己的详细的自…
-
暑假工地预算员实习总结报告
实习总结报告光阴似箭日月如梭,不知不觉中我在工地实习已经进行了一个半月,在这短短的一个半月中,我受益匪浅,实习过程中的点点滴滴,让…
-
高中有机化学方程式总结
一.各类化合物的鉴别方法1.烯烃、二烯、炔烃:(1)溴的四氯化碳溶液,红色腿去(2)高锰酸钾溶液,紫色腿去。2.含有炔氢的炔烃:(…