教材背景：

归纳是一种由特殊事例导出一般规律的思维方法．归纳推理分完全归纳推理与不完全归纳推理两种．不完全归纳推理只根据一类事物中的部分对象具有的共同性质，推断该类事物全体都具有的性质，这种推理方法，在数学推理论证中是不允许的．完全归纳推理是在考察了一类事物的全部对象后归纳得出结论来．数学归纳法是用来证明某些与正整数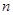有关的数学命题的一种推理方法，在数学问题的解决中有着广泛的应用．

教学课题：数学归纳法

教材分析：

   “数学归纳法”既是高中代数中的一个重点和难点内容，也是一种重要的数学方法。它贯通了高中代数的几大知识点：不等式，数列，三角函数……在教学过程中，教师应着力解决的内容是：使学生理解数学归纳法的实质，掌握数学归纳法的证题步骤（特别要注意递推步骤中归纳假设的运用和恒等变换的运用）。只有真正了解了数学归纳法的实质，掌握了证题步骤，学生才能信之不疑，才能用它灵活证明相关问题。本节课是数学归纳法的第一节课，有两大难点：使学生理解数学归纳法证题的有效性；递推步骤中归纳假设的利用。不突破以上难点，学生往往会怀疑数学归纳法的可靠性，或者只是形式上的模仿而不知其所以然。这会对以后的学习造成极大的阻碍。根据本节课的教学内容和学生实际水平，本节课采用“引导发现法”和“讲练结合法”。通过课件的动画模拟展示，引发和开启学生的探究热情，通过“师生”和“生生”的交流合作，掌握概念的深层实质。

 教学目标

1、知识和技能目标

(1)了解数学推理的常用方法（归纳法）

(2)了解数学归纳法的原理及使用范围。

(3)初步掌握数学归纳法证题的两个步骤和一个结论。

(4)会用数学归纳法证明一些简单的等式问题。

2、过程与方法目标

通过对归纳法的复习，说明不完全归纳法的弊端，通过多米诺骨牌实验引出数学归纳法的原理，使学生理解理论与实际的辨证关系。在学习中培养学生探索发现问题、提出问题的意识，解决问题和数学交流的能力,学会用总结、归纳、演绎类比探求新知识。

3.情感态度价值观目标

通过对问题的探究活动，亲历知识的构建过程，领悟其中所蕴涵的数学思想；体验探索中挫折的艰辛和成功的快乐，感悟“数学美”，激发学习热情，培养他们手脑并用，多思勤练的好习惯和勇于探索的治学精神。初步形成正确的数学观，创新意识和科学精神。

 教学重点和难点

     教学重点：（1）使学生理解数学归纳法的实质 。

（2）掌握数学归纳法证题步骤,尤其是递推步骤中归纳假设和恒等变换的运用。

教学难点：

（1）数学归纳法的原理；

 教学方法：讲授法、引导发现法、类比探究法、讲练结合法

教学过程：

（一）复习引入

问题（1）袋中有5个小球，如何证明它们都是红色的？（完全归纳法）

问题（2）某人站在学校门口，看到连续有20个男生进入学校，于是深有感触的说这个学校的学生都是男生。（不完全归纳法）

（二）新课讲解

1、多米诺骨牌实验

要使所有的多米诺骨牌一一倒下？需要几个步骤才能做到？

（1）第一张牌被推倒    （奠基作用）

（2）任意一张牌倒下必须保证它的下一张牌倒下  （递推作用）

于是可以获得结论：多米诺骨牌会全部倒下。

例1、证明：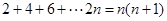   

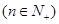
证明：（1）当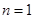时，左边=2，右边=2，等式成立。

（2）假设时等式成立，即

那么，当时，

                   

                  

所以，时等式也成立。

由（1）和（2）可知，等式对于任何正整数都成立。

2、归纳总结

数学归纳法证明步骤：

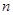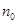(1)验证当取第一个值（如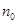=1或2时）命题正确。

(2)假设当时命题正确，证明时命题也正确。

3．基础反馈

①用数学归纳法证明：在验证n=1成立时，左边计算所得的结果是（ C  ）

A．1                 B.    C．       D.

②用数学归纳法证明命题时，假设                那么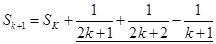 

③判断下面的证明过程是否正确，如果不正确错在哪？

证明：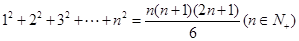

证明：（1）当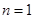时，左边=1，右边=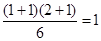等式成立

（2）假设当时等式成立即

当时代入得

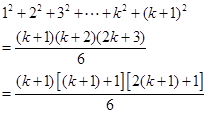
所以当时等式成立

由（1）和（2）可知等式对一切正整数均成立。

（三）、课堂小结

（1）理解数学归纳法的原理

（2）数学归纳法的两个步骤缺一不可，前者是基础，后者是递推依据，最终给出结论。

（3）数学归纳法主要应用于解决与正整数有关的数学问题。

（四）、作业 : P₃₇    2  P₃₉ 1 

（五）、课后练习及探究:

   练习：P₃₇ (1)、(3)

   探究：下面是某同学用数学归纳法证明命题

的过程，你认为他的证法正确吗？为什么？                                                               

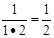   证明：（1）当 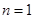时  左边=           右边  等式成立

（2）假设当时命题成立即

     

那么时, 左边

=右边

          即时命题成立

由（1）和（2）知，对一切自然数命题均成立。

（六）、预习：用数学归纳法证明不等式

（七）、课后反思

1.数学归纳法是一种用于证明与自然数n有关的命题的正确性的证明方法．它的操作步骤简单、明确，教学重点不应该是方法的应用．我认为不能把教学过程当作方法的灌输，技能的操练．为此，我设想强化数学归纳法产生过程的教学，把数学归纳法的产生寓于对归纳法的分析、认识当中，为使用它打下良好的基础，而且可以强化归纳思想的教学，这不仅是对中学数学中以演绎思想为主的教学的重要补充，也是引导学生发展创新能力的良机．

2．在教学方法上，这里运用了在教师指导下的师生共同讨论、探索的方法．目的是加强学生对教学过程的参与．为了使这种参与有一定的智能度，教师应做好发动、组织、引导和点拨．学生的思维参与往往是从问题开始的，本节课按照思维次序编排了一系列问题，让学生投入到思维活动中来，把本节课的研究内容置于问题之中，在逐渐展开中，引导学生用已学的知识、方法予以解决，并获得知识体系的更新与拓展．

3．运用数学归纳法证明与正整数有关的数学命题，两个步骤缺一不可．理解数学归纳法中的递推思想，尤其要注意其中第二步，证明n＝k＋1命题成立时必须要用到n＝k时命题成立这个条件．这些内容都将放在下一课时完成，这种理解不仅使我们能够正确认识数学归纳法的原理与本质，也为证明过程中第二步的设计指明了思维方向．

 

第二篇：数学归纳法学案

课    题：数学归纳法及其应用举例

一、教学要求：

（1）了解数学归纳法的原理，并能以递推思想作指导；

（2）理解数学归纳法的操作步骤，能用数学归纳法证明一些简单的数学命题，并能严格按照数学归纳法证明问题的格式书写.

二、基础梳理：

1.什么叫数学归纳法？

2.用数学归纳法证明一个与正整数有关的命题的步骤：

总结：递推基础不可少，归纳假设要用到，结论写明莫忘掉.

三、例题

              类型一 证明等式

例1　用数学归纳法证明

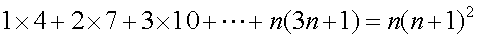分析

1）第一步应做什么？此时n0=      ，左　　　　  ，

2) 当n=k时，等式左边共有　　项，

第k项是　　　　　              　　。　　

假设n=k时命题成立，即________________________________

3）当n=k+1时，命题的形式是　　　　　              　　

4）此时，左边增加的项是　　　　　              　　

5)从左到右如何变形？　　　　　              　　

证明：

变式训练

1、用数学归纳法证:

 

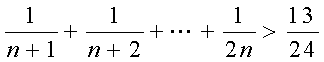
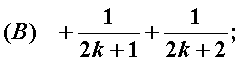(n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时，不等式左边的变化是（     ）：

 

2、用数学归纳法证:

 

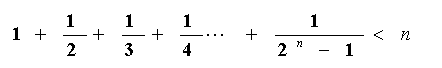
(n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时，左式所需添加的项数为（     ）：

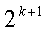Ａ.１项              Ｂ.    　项

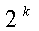
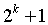Ｃ.　　 项         Ｄ.　　  项

类型二 证明整除问题

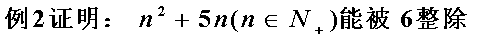
证明：

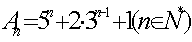变式训练:用数学归纳法证明:                      能被8整除.

               类型三 证明不等式问题

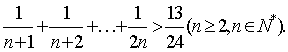例3:用数学归纳法证明:

分析： 此题关键在于从n=k到n=k+1不等式左端的变化

证明：

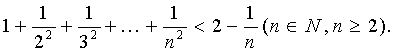变式训练

求证:

四、小结 ：

   1、数学归纳法有哪些应用？

  2、第二步中从n=k到n=k+1应注意哪些问题，有哪些技巧方法？

五、课后作业：

（一）、必做题 

1、用数学归纳法证明下式

(1)当n=1时,左边有_____项,右边有_____项；

(2)当n=k时,左边有_____项,右边有_____项；

(3)当n=k+1时,左边有_____项,右边有_____项；

(4)等式的左右两边,由n=k到n=k+1时有什么不同?

左边增加两项:_____________

右边增加两项:  __________,减少一项:________

2、用数学归纳法证明用数学归纳法证明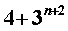能被13整除，

（其中n∈N*）

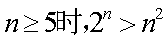3、用数学归纳法证明当

（二）、选做题

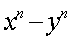1、用数学归纳法证明:当n为正偶数时,         能被x+y整除.

2、平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=n(n-1)/2.