解三角形知识点总结及典型例题
课前复习
两角和与差的正弦、余弦、正切公式
1两角和与差的正弦公式,
sin(α+β)=sinαcosβ+cosαsinβ,
sin(α-β)=sinαcosβ-cosαsinβ.
2两角和与差的余弦公式,
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcos+sinαsinβ
3两角和、差的正切公式
tan(α+β)=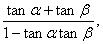 (
(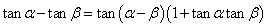 );
);
tan(α-β)=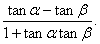 (
(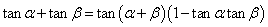 ).
).
简单的三角恒等变换
二倍角的正弦、余弦和正切公式:
⑴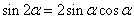 .
.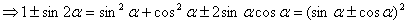
⑵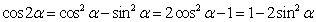
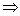 升幂公式
升幂公式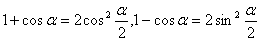
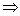 降幂公式
降幂公式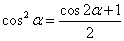 ,
,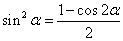
⑶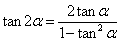
默写上述公式,检查上次的作业课本上的!
解三角形知识点总结及典型例题

第二篇:初中三角函数知识点总结及典型习题
初三下学期锐角三角函数知识点总结及典型习题
1、勾股定理:直角三角形两直角边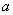 、
、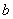 的平方和等于斜边
的平方和等于斜边 的平方。
的平方。 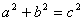
2、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B):
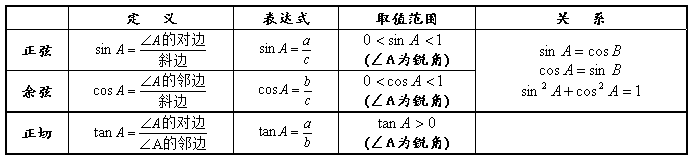
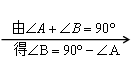
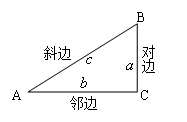 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
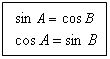
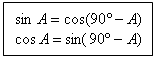
5、30°、45°、60°特殊角的三角函数值(重要)

6、正弦、余弦的增减性:
当0°≤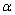 ≤90°时,sin
≤90°时,sin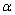 随
随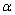 的增大而增大,cos
的增大而增大,cos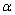 随
随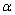 的增大而减小。
的增大而减小。
7、正切、的增减性:
当0°<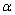 <90°时,tan
<90°时,tan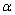 随
随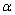 的增大而增大,
的增大而增大,
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系: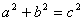 ;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)
;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)
2、应用举例:
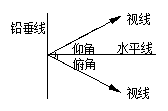
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
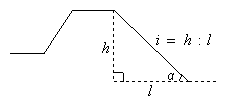
(2)坡面的铅直高度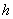 和水平宽度
和水平宽度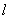 的比叫做坡度(坡比)。用字母
的比叫做坡度(坡比)。用字母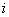 表示,即
表示,即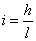 。坡度一般写成
。坡度一般写成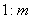 的形式,如
的形式,如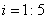 等。
等。
把坡面与水平面的夹角记作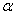 (叫做坡角),那么
(叫做坡角),那么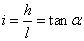 。
。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。如图4,OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向),
南偏西60°(西南方向), 北偏西60°(西北方向)。

例1:已知在 中,
中, ,则
,则 的值为( )
的值为( )
A. B.
B.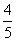 C.
C.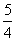 D.
D.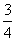
【解析】本题考查三角函数的定义和勾股定理,在RTΔABC中,∠C=90°,则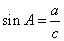 ,
,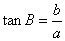 和
和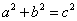 ;由
;由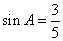 知,如果设
知,如果设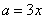 ,则
,则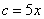 ,结合
,结合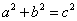 得
得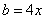 ;∴
;∴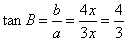 ,所以选A.
,所以选A.
例2: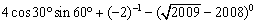 =______.
=______.
【解析】本题考查特殊角的三角函数值.零指数幂.负整数指数幂的有关运算,
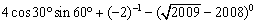 =
=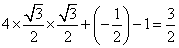 ,故填
,故填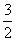 .
.
1. 某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为( C )
A.8米 B.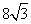 米 C.
米 C.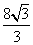 米 D.
米 D.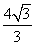 米
米
2. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角是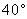 ,则梯子底端到墙的距离为( B )
,则梯子底端到墙的距离为( B )
A. B.
B.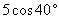 C.
C.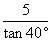 D.
D.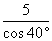
3. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( B )
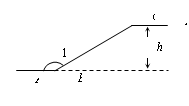 A.
A.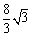 m B.4 m
m B.4 m
C.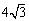 m D.8 m
m D.8 m
4. 河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比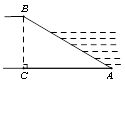 是1:
是1: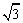 (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( A )
(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( A )
A.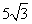 米 B. 10米
米 B. 10米
C.15米 D.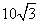 米
米
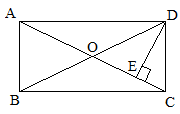
5.如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是( D )
A.3 B.5 C.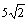 D.
D.
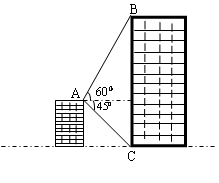 6. 如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为 82.0 米(精确到0.1).(参考数据:
6. 如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为 82.0 米(精确到0.1).(参考数据:
 )
)
7. 如图,热气球的探测器显示,从热气球 看一栋大楼顶部
看一栋大楼顶部 的俯角为
的俯角为 ,看这栋大楼底部
,看这栋大楼底部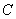 的俯角为
的俯角为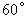 ,热气球
,热气球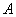 的高度为240米,求这栋大楼的高度.
的高度为240米,求这栋大楼的高度.
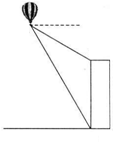 解:过点
解:过点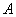 作直线
作直线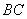 的垂线,垂足为点
的垂线,垂足为点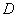 .
.
则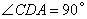 ,
,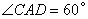 ,
,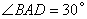 ,
,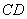 =240米.
=240米.
在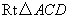 中,
中,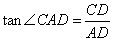 ,
,
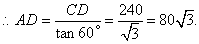
在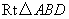 中,
中,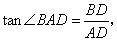
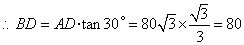 .
.

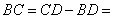 240
240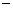 80=160.
80=160.
答:这栋大楼的高为160米.
8. 如图所示,城关幼儿园为加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D、B、C在同一水平面上.
(1)改善后滑滑板会加长多少米?
(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.
(参考数据: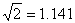 ,
,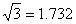 ,
,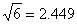 ,以上结果均保留到小数点后两位.)
,以上结果均保留到小数点后两位.)
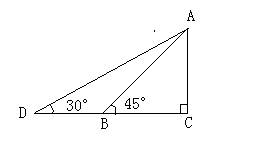
解:(1)在Rt△ABC中,∠ABC=45°
∴AC=BC=AB·sin45°=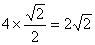
在Rt△ADC中,∠ADC=30°
∴AD= 
∴AD-AB=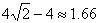
∴改善后滑滑板会加长约1.66米.
(2)这样改造能行,理由如下:
∵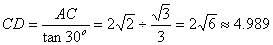
∴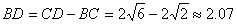
∴6-2.07≈3.93>3
∴这样改造能行.
9.求值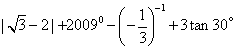 1.解:原式=
1.解:原式= 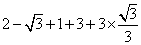
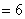
10. 计算: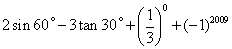 2.原式=
2.原式=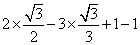 =0.
=0.
第三篇:高一数学解三角形知识点总结及习题练习
解三角形

2[课前热身]
1.(教材习题改编)已知△ABC中,a=,b=,B=60°,那么角A等于( )
A.135° B.90°
C.45° D.30°
2.在△ABC中, ,则A等于( )
,则A等于( )
A.60° B.45° C.120° D.30°
3.在△ABC中,若A=120°,AB=5,BC=7,则△ABC的面积是( )
A. B. C. D.
4.(2010年高考广东卷)已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=,A+C=2B,则sinA=________.
5.
5.在△ABC中,如果A=60°,c=,a=,则△ABC的形状是________.
3[考点突破]
考点一 正弦定理的应用
利用正弦定理可解决以下两类三角形:一是已知两角和一角的对边,求其他边角;二是已知两边和一边的对角,求其他边角.
例1、(1)(20##年高考山东卷)在△ABC中,角A,B,C所对的边分别为a,b,c.若a=,b=2,sin B+cos B=,则角A的大小为________.
(2)满足A=45°,a=2,c=的△ABC的个数为________.
考点二 余弦定理的应用
利用余弦定理可解两类三角形:一是已知两边和它们的夹角,求其他边角;二是已知三边求其他边角.由于这两种情况下的三角形是惟一确定的,所以其解也是惟一的.
例2、在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=.
(1)若△ABC的面积等于,求a,b的值;
(2)若sinB=2sinA,求△ABC的面积.
考点三三角形形状的判定
判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
例3、(20##年高考辽宁卷)在△ABC中,a,b,c分别为内角A,B,C的对边,且
2asin A=(2b+c)sin B+(2c+b)sin C.
(1)求A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
互动探究
1 若本例条件变为:sinC=2sin(B+C)cosB,试判断三角形的形状..
方法感悟:
方法技巧
解三角形常见题型及求解方法
(1)已知两角A、B与一边a,由A+B+C=180°及==,可求出角C,再求出b,c.
(2)已知两边b,c与其夹角A,由a2=b2+c2-2bccosA, 求出a,再由正弦定理,求出角B,C.
(3)已知三边a、b、c,由余弦定理可求出角A、B、C.
(4)已知两边a、b及其中一边的对角A,由正弦定理=求出另一边b的对角B,由C=π-(A+B),求出C,再由=,求出c,而通过=求B时,可能出现一解,两解或无解的情况,其判断方法如下表:

失误防范
1.用正弦定理解三角形时,要注意解题的完整性,谨防丢解.
2.要熟记一些常见结论,如三内角成等差数列,则必有一角为60°;若三内角的正弦值成等差数列,则三边也成等差数列;三角形的内角和定理与诱导公式结合产生的结论:sinA=sin(B+C),cosA=-cos(B+C),sin=cos,sin2A=-sin2(B+C),cos2A=cos2(B+C)等.
3.对三角形中的不等式,要注意利用正弦、余弦的有界性进行适当“放缩”.
五、规范解答
(本题满分12分)(20##年高考大纲全国卷Ⅱ)在△ABC中,D为边BC上的一点,BD=33,sinB=,cos∠ADC=,求AD的长.
【解】 由cos∠ADC=>0知∠B<,
由已知得cosB=,sin∠ADC=,4分
从而sin∠BAD=sin(∠ADC-∠B)
=sin∠ADCcosB-cos∠ADCsinB
=×-×=.9分
由正弦定理得=,
所以AD===25.12分
【名师点评】 本题主要考查正弦定理、三角恒等变换在解三角形中的应用,同时,对逻辑推理能力及运算求解能力进行了考查.本题从所处位置及解答过程来看,难度在中档以下,只要能分析清各量的关系,此题一般不失分.出错的原因主要是计算问题.
名师预测
1.在△ABC中,a=15,b=10,A=60°,则cosB=( )
A.- B.
C.- D.
2.已知△ABC中,角A、B、C的对边分别为a、b、c,且S△ABC=,那么角C=________.
3.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b-c)·cosA-acosC=0.
(1)求角A的大小;
(2)若a=,S△ABC=,试判断△ABC的形状,并说明理由.
解:(1)法一:∵(2b-c)cosA-acosC=0,
由正弦定理得,
(2sinB-sinC)cosA-sinAcosC=0,
∴2sinBcosA-sin(A+C)=0,
即sinB(2cosA-1)=0.
∵0<B<π,
∴sinB≠0,∴cosA=.
∵0<A<π,∴A=.
法二:∵(2b-c)cosA-acosC=0,
由余弦定理得,
(2b-c)·-a·=0,
整理得b2+c2-a2=bc,
∴cosA==.
∵0<A<π,∴A=.
(2)∵S△ABC=bcsinA=,
即bcsin=,
∴bc=3,①
∵a2=b2+c2-2bccosA,
∴b2+c2=6,②
由①②得b=c=,
∴△ABC为等边三角形.
课后作业
1 在△ABC中,角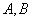 均为锐角,且
均为锐角,且 则△ABC的形状是( )
则△ABC的形状是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰三角形
2 边长为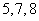 的三角形的最大角与最小角的和是( )
的三角形的最大角与最小角的和是( )
A.  B.
B.  C.
C.  D.
D. 
3 在 △ABC中,
△ABC中,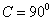 ,则
,则 的最大值是_______________.
的最大值是_______________.
4 在△ABC中,若 _________.
_________.
5 已知△ABC的三个内角分别为A,B,C,向量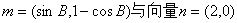 夹角的余弦角为
夹角的余弦角为
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围.
的取值范围.
6 △ABC中,角A、B、C的对边分别为a,b,c.
(Ⅰ)若 ,求cosA的值;
,求cosA的值;
(Ⅱ)若A∈[ ,
, ],求
],求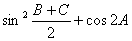 的取值范围.
的取值范围.
7 在△ABC中,求证:
8 在锐角△ABC中,求证: .
.
-
高一数学解三角形知识点总结及习题练习
解三角形一、基础知识梳理asinAsinBsinCb2Rc2R=b=c=2R(R为△ABC外接圆半径),了解正弦定理以下变形:a?…
-
解三角形知识点总结及典型例题
课前复习两角和与差的正弦、余弦、正切公式1两角和与差的正弦公式,sin(α+β)=sinαcosβ+cosαsinβ,sin(α-…
-
高中数学必修5__解三角形知识点总结与练习
解三角形一、知识点总结1.内角和定理:在?ABC中,A?B?C??;sin(A?B)?sinC;cos(A?B)??cosC;si…
-
必修5 解三角形知识点归纳总结
第一章解三角形一.正弦定理:1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即2.变形:1)a…
-
解三角形知识点归纳
一正弦定理(一)知识与工具:abc???2R。正弦定理:在△ABC中,sinAsinBsinC在这个式子当中,已知两边和一角或已知…
-
高中数学必修5__解三角形知识点总结与练习
解三角形一、知识点总结1.内角和定理:在?ABC中,A?B?C??;sin(A?B)?sinC;cos(A?B)??cosC;si…
-
高一数学解三角形知识点总结及习题练习
解三角形一、基础知识梳理asinAsinBsinCb2Rc2R=b=c=2R(R为△ABC外接圆半径),了解正弦定理以下变形:a?…
-
全等三角形知识点总结
定义能够完全重合的两个三角形称为全等三角形。(注:全等三角形是相似三角形中的特殊情况)当两个三角形完全重合时,互相重合的顶点叫做对…
-
三角形知识点总结
第一章图形的初步认识考点一、线段垂直平分线,角的平分线,垂线1、线段垂直平分线的性质定理及逆定理垂直于一条线段并且平分这条线段的直…
-
三角形知识点总结(完)
三角形1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL(Rt△≌Rt△)2…
-
高中数学 第二章 正余弦定理在解决三角形问题中的应用知识归纳典型例题素材 北师大版必修5
正余弦定理在解决三角形问题中的应用知识点归纳:1.正弦定理:abc???2R;sinAsinBsinCabc形式二:sinA=;s…