必修5 解三角形知识点归纳总结
第一章 解三角形
一.正弦定理:
1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即 2.变形:1)
asinA
?
bsinB
??
csinCasin?
?2R?
bsin?
(其中R是三角形外接圆的半径)
?
csinC
a?b?csin??sin??sinC
.
2)化边为角:a:b:c?sinA:sinB:sinC;
ab?sinAsinB
; bc?sinBsinC
; ac?sinAsinC
;
3)化边为角:a?2RsinA,b?2RsinB,c?2RsinC 4)化角为边:
sinAsinB
?aba;
,
sinBsinC
5)化角为边: sinA?
2R
csinCcbc
sinB?,sinC?
2R2R
?
b
;
sinA
?
a
;
3. 利用正弦定理可以解决下列两类三角形的问题: ①已知两个角及任意—边,求其他两边和另一角; 例:已知角B,C,a,
解法:由A+B+C=180o ,求角A,由正弦定理
ac?sinAsinC
;求出b与c
ab?sinAsinB
; bc?sinBsinC
;
②已知两边和其中—边的对角,求其他两个角及另一边。 例:已知边a,b,A, 解法:由正弦定理用正弦定理
4.△ABC中,已知锐角A,边b,则
ac?sinAsinC
ab?sinAsinB
求出角B,由A+B+C=180o 求出角C,再使
求出c边
①a?bsinA时,B无解;
②a?bsinA或a?b时,B有一个解; ③bsinA?a?b时,B有两个解。
如:①已知A?60?,a?2,b?23,求B(有一个解)
②已知A?60?,b?2,a?23,求B(有两个解) 注意:由正弦定理求角时,注意解的个数。
二.三角形面积 1.S?ABC?
12
absinC?
12
bcsinA?
12acsinB
2. S?ABC?3. S?ABC?4. S?ABC?
12
(a?b?c)r,其中r是三角形内切圆半径.
p(p?a)(p?b)(p?c), 其中p?abc4R
12
(a?b?c),
,R为外接圆半径
5.S?ABC?2R2sinAsinBsinC,R为外接圆半径
三.余弦定理
1.余弦定理:三角形中任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的2倍,即 a2?b2?c2?2bccosA b2?a2?c2?2accosB c2?a2?b2?2abcosC 2.变形:cosA?
b?c?a
2bc
2
2
2
cosB?
a?c?b
2aca?b?c
2ab
2
2
222
2
cosC?
12
注意整体代入,如:a2?c2?b2?ac?cosB?3.利用余弦定理判断三角形形状:
设a、b、c是???C的角?、?、C的对边,则:
①若,
②若c2?b2?a2?A为直角
,所以为锐角
③若钝角三角形
4.利用余弦定理可以解决下列两类三角形的问题: 1)已知三边,求三个角
, 所以为钝角,
则是
2)已知两边和它们的夹角,求第三边和其他两个角
四、应用题
1.已知两角和一边(如A、B、C),由A+B+C = π求C,由正弦定理求a、
b.
2.已知两边和夹角(如a、b、c),应用余弦定理求c边;再应用正弦定理先求较短边所对的角,然后利用A+B+C = π,求另一角.
3.已知两边和其中一边的对角(如a、b、A),应用正弦定理求B,由A+B+C = π求C,再由正弦定理或余弦定理求c边,要注意解可能有多种情况.
4.已知三边a、b、c,应用余弦定理求A、B,再由A+B+C = π,求角C.
5.方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目
标的方向线所成的角(一般指锐角),通常表达成.正北或正南,北偏东××度, 北偏西××度,南偏东××度,南偏西××度.
6.俯角和仰角的概念:在视线与水平线所成的角中,视线在水平线上 方的角叫仰角,视线在水平线下方的角叫俯角.
五、三角形中常见的结论
1)三角形三角关系:A+B+C=180°;C=180°—(A+B); 2)三角形三边关系: 两边之和大于第三边:
,
,
;
铅
直线
视线
水平线
两边之差小于第三边:,,;
3)在同一个三角形中大边对大角:A?B?a?b?sinA?sinB 4) 三角形内的诱导公式:
sin(A?B)?sinC,cos(A?B)??cosC,tan(A?B)??tanC,
?CCsin?)cos)
A?B?C? ta?tan?)?
?CC222
cos?)sin)
222
5) 两角和与差的正弦、余弦、正切公式 (1)sin(α±β)=sin αcos β±cos αsin β.
(2)cos(α±β)=cos αcos β?sin αsin β. tan α±tan β
(3)tan(α±β)=1?tan αtan β
6) 二倍角的正弦、余弦、正切公式 (1)sin 2α=2sin αcos α.
(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α. (3)sin2??
(4)tan 2α=
7) 三角形的五心:
1?cos2?
2
;cos??
2
1?cos2?
2
2tan α1-tan2α
.
垂心——三角形的三边上的高相交于一点 重心——三角形三条中线的相交于一点 外心——三角形三边垂直平分线相交于一点 内心——三角形三内角的平分线相交于一点
旁心——三角形的一条内角平分线与其他两个角的外角平分线交于一点
第二篇:必修5 数列知识点归纳总结
第二章 数列
一、数列的概念:
1、数列、数列的项及其符号表示:
按一定次序排列的一列数叫做数列。数列中的每一个数都叫做这个数列的项。
数列a1,a2,a3,??,an记为{an}
2、数列的通项公式:如果数列{an}的第n项与n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式。
3、有穷数列与无穷数列:若数列{an}的项数是有限的,则称数列{an}为有穷数列。若数列{an}的项数是无限的,则称数列{an}为无穷数列。
4、递增数列:在数列{an}中,若an?1≥an对任意正整数n都成立,则称数列{an}为递增数列;
5、递减数列:在数列{an}中,?n?N,an?1?an则称{an}为递减数列;
6、常数列:在数列{an}中,?n?N,an?1?an则称{an}为常数列;
7、摆动数列:在数列{an}中,自第二项起,有些项大于它的前一项,有些小于它们的前一项,则称{an}为摆动数列。
8、数列的递推关系:如果已知数列{an}的第一项(或前几项),且任一项an与它的前一项an?1(或前几项)之间的关系可以用一个式子来表示,那么这个式子就叫做这个数列的递推公式。
9、数列{an}的前n项和Sn与第n项an之间的关系是: ??
an???S1
?Sn?Sn?1(n≥2) (n-1)
二、等差数列:
1、等差数列的定义:
如果一个数列{an}自第2项起,每一项与它前一项的差等于同一个常数,即an?1?an?d(n?2,d是一个与n无关的常数),则数列{an}叫做等差数列。
2、等差数列的通项公式:an?a1?(n?1)d
3、等差数列的单调性:设等差数列{an}的公差d,当d>0,等差数列{an}为递增数列;当d<0时,等差数列{an}为递减速;d=0时{an}为常数列。
4、等差中项:a、b、c 成等差数列,则称b为a、c的等差中项。
a?c? a、b、c成等差数列。 b为a、c的等差中项?b-a=c-b?2b=a+c?或b?2
5、等差数列的常用性质:设等差数列{an}的公差为d ,k、l、m、n?N*.
1)若k+l=m+n则ak?al?am?an 2)若m+n=2k则am?an?2ak
3)an?am?(n?m)d(n?m) 4)d?
5)a1?an?a2?an?1?a3?an?2?.....
6、等差数列{an}前n项和:
11SN?n(a1?an)?na1?n(n?1)d?an2?bn为常数,(a、b为常数,公22
an?a1am?ak? n?1m?k
差为d
7、项数(下标)的“等和”性质:
n(a1?an)n(a2?an?1)n(am?an?m?1)sn??? 222
8、设等差数列{an}、?bn?的前n项和分别为Sn、Tn,则anS2n?1 ?bnT2n?1
9、“片段和”性质:等差数列{an}的公差为d,前n项和为Sn,则SK,S2K?SK,
2S3K?S2K,??(K?N?)成等差数列,其公差为kd。
10、若等差数列{an}的项数为2n(n?N*),则S2n?n(an?an?1)(其中为中间两项),且
S偶?S奇?nd,S奇S偶?an。 an?1
11、若等差数列{an}的项数为2n-1,则S2n?1?(2n?1)an,(an为中间项)且
S奇?S偶?an,
三、等比数列
1、等比数列的定义: S奇S偶?n n?1
如果一个数列{an}从第二项起,每一项与它的的比等于同一个常数,即an?1?q(n?1, an
n?N?,q 是与n无关的常数),这个数列就叫做等比数列。
2、等比数列{an}的通项公式:an?a1qn?1.
注意:在等比数列{an}中,an?0 ,q?0。
3、等比中项:a、G、b成等比数列,则G叫做a与b的等比中项。a、G、b成等比数列?G2?ab,a2n?1?anan?2
4、等比数列的常用性质:若{an}是等比数列,m、n、k、l?N?
①k+l=m+n?akal?aman
2②m+n=2k?aman?ak
③an?amqn?m
④a1an?a2an?1?a3an?2?akan?k?1(n为正奇数)
5、单调性:设等比数列{an}的公比为q
①当q>1,a1?0或0<q<1,a1?0时,{an}递增;
②当a1?0,0?a?1或a1?0,q?1时{an}递减;
③当q=1时,{an}为常数列; ④当q=-1时,{an}为摆动数列;
na1(q?1)??n6、等比数列{an}的前n项和Sn??a1(1?q)a1?anq ??A?Aqn(q?1)?1?q?1?q
7、设等比数列{an}的前m项和为Sm则Sm,S2m?Sm,S3m?S2m,??仍构
2成公比为qm的等比数列,且有?S2m?Sm??Sm?(S3m?S2m)
8、若数列{an}的前项和Sn?an?1(a?0,a?1),则{an}是等比数列。
9、若等比数列{an}的公比为q,前项和为Sn,则Sn?m?Sn?qnSm
10、若等比数列{an}的项数为2n(n?N*),则S偶
S奇?q
a1?a2n?2 (q?1且q??1),1?q11、若等比数列{an}的项数为2n?1(n?N*),则S奇-S偶?
第三篇:高一数学解三角形知识点总结及习题练习
解三角形

2[课前热身]
1.(教材习题改编)已知△ABC中,a=,b=,B=60°,那么角A等于( )
A.135° B.90°
C.45° D.30°
2.在△ABC中, ,则A等于( )
,则A等于( )
A.60° B.45° C.120° D.30°
3.在△ABC中,若A=120°,AB=5,BC=7,则△ABC的面积是( )
A. B. C. D.
4.(2010年高考广东卷)已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=,A+C=2B,则sinA=________.
5.
5.在△ABC中,如果A=60°,c=,a=,则△ABC的形状是________.
3[考点突破]
考点一 正弦定理的应用
利用正弦定理可解决以下两类三角形:一是已知两角和一角的对边,求其他边角;二是已知两边和一边的对角,求其他边角.
例1、(1)(20##年高考山东卷)在△ABC中,角A,B,C所对的边分别为a,b,c.若a=,b=2,sin B+cos B=,则角A的大小为________.
(2)满足A=45°,a=2,c=的△ABC的个数为________.
考点二 余弦定理的应用
利用余弦定理可解两类三角形:一是已知两边和它们的夹角,求其他边角;二是已知三边求其他边角.由于这两种情况下的三角形是惟一确定的,所以其解也是惟一的.
例2、在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=.
(1)若△ABC的面积等于,求a,b的值;
(2)若sinB=2sinA,求△ABC的面积.
考点三三角形形状的判定
判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
例3、(20##年高考辽宁卷)在△ABC中,a,b,c分别为内角A,B,C的对边,且
2asin A=(2b+c)sin B+(2c+b)sin C.
(1)求A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
互动探究
1 若本例条件变为:sinC=2sin(B+C)cosB,试判断三角形的形状..
方法感悟:
方法技巧
解三角形常见题型及求解方法
(1)已知两角A、B与一边a,由A+B+C=180°及==,可求出角C,再求出b,c.
(2)已知两边b,c与其夹角A,由a2=b2+c2-2bccosA, 求出a,再由正弦定理,求出角B,C.
(3)已知三边a、b、c,由余弦定理可求出角A、B、C.
(4)已知两边a、b及其中一边的对角A,由正弦定理=求出另一边b的对角B,由C=π-(A+B),求出C,再由=,求出c,而通过=求B时,可能出现一解,两解或无解的情况,其判断方法如下表:

失误防范
1.用正弦定理解三角形时,要注意解题的完整性,谨防丢解.
2.要熟记一些常见结论,如三内角成等差数列,则必有一角为60°;若三内角的正弦值成等差数列,则三边也成等差数列;三角形的内角和定理与诱导公式结合产生的结论:sinA=sin(B+C),cosA=-cos(B+C),sin=cos,sin2A=-sin2(B+C),cos2A=cos2(B+C)等.
3.对三角形中的不等式,要注意利用正弦、余弦的有界性进行适当“放缩”.
五、规范解答
(本题满分12分)(20##年高考大纲全国卷Ⅱ)在△ABC中,D为边BC上的一点,BD=33,sinB=,cos∠ADC=,求AD的长.
【解】 由cos∠ADC=>0知∠B<,
由已知得cosB=,sin∠ADC=,4分
从而sin∠BAD=sin(∠ADC-∠B)
=sin∠ADCcosB-cos∠ADCsinB
=×-×=.9分
由正弦定理得=,
所以AD===25.12分
【名师点评】 本题主要考查正弦定理、三角恒等变换在解三角形中的应用,同时,对逻辑推理能力及运算求解能力进行了考查.本题从所处位置及解答过程来看,难度在中档以下,只要能分析清各量的关系,此题一般不失分.出错的原因主要是计算问题.
名师预测
1.在△ABC中,a=15,b=10,A=60°,则cosB=( )
A.- B.
C.- D.
2.已知△ABC中,角A、B、C的对边分别为a、b、c,且S△ABC=,那么角C=________.
3.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b-c)·cosA-acosC=0.
(1)求角A的大小;
(2)若a=,S△ABC=,试判断△ABC的形状,并说明理由.
解:(1)法一:∵(2b-c)cosA-acosC=0,
由正弦定理得,
(2sinB-sinC)cosA-sinAcosC=0,
∴2sinBcosA-sin(A+C)=0,
即sinB(2cosA-1)=0.
∵0<B<π,
∴sinB≠0,∴cosA=.
∵0<A<π,∴A=.
法二:∵(2b-c)cosA-acosC=0,
由余弦定理得,
(2b-c)·-a·=0,
整理得b2+c2-a2=bc,
∴cosA==.
∵0<A<π,∴A=.
(2)∵S△ABC=bcsinA=,
即bcsin=,
∴bc=3,①
∵a2=b2+c2-2bccosA,
∴b2+c2=6,②
由①②得b=c=,
∴△ABC为等边三角形.
课后作业
1 在△ABC中,角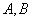 均为锐角,且
均为锐角,且 则△ABC的形状是( )
则△ABC的形状是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰三角形
2 边长为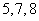 的三角形的最大角与最小角的和是( )
的三角形的最大角与最小角的和是( )
A.  B.
B.  C.
C.  D.
D. 
3 在 △ABC中,
△ABC中,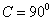 ,则
,则 的最大值是_______________.
的最大值是_______________.
4 在△ABC中,若 _________.
_________.
5 已知△ABC的三个内角分别为A,B,C,向量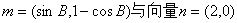 夹角的余弦角为
夹角的余弦角为
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围.
的取值范围.
6 △ABC中,角A、B、C的对边分别为a,b,c.
(Ⅰ)若 ,求cosA的值;
,求cosA的值;
(Ⅱ)若A∈[ ,
, ],求
],求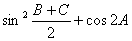 的取值范围.
的取值范围.
7 在△ABC中,求证:
8 在锐角△ABC中,求证: .
.
-
高一数学解三角形知识点总结及习题练习
解三角形一、基础知识梳理asinAsinBsinCb2Rc2R=b=c=2R(R为△ABC外接圆半径),了解正弦定理以下变形:a?…
-
解三角形知识点总结及典型例题
课前复习两角和与差的正弦、余弦、正切公式1两角和与差的正弦公式,sin(α+β)=sinαcosβ+cosαsinβ,sin(α-…
-
高中数学必修5__解三角形知识点总结与练习
解三角形一、知识点总结1.内角和定理:在?ABC中,A?B?C??;sin(A?B)?sinC;cos(A?B)??cosC;si…
-
必修5 解三角形知识点归纳总结
第一章解三角形一.正弦定理:1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即2.变形:1)a…
-
解三角形知识点归纳
一正弦定理(一)知识与工具:abc???2R。正弦定理:在△ABC中,sinAsinBsinC在这个式子当中,已知两边和一角或已知…
-
高中数学必修5__解三角形知识点总结与练习
解三角形一、知识点总结1.内角和定理:在?ABC中,A?B?C??;sin(A?B)?sinC;cos(A?B)??cosC;si…
-
解三角形知识点总结及典型例题
课前复习两角和与差的正弦、余弦、正切公式1两角和与差的正弦公式,sin(α+β)=sinαcosβ+cosαsinβ,sin(α-…
-
高一数学解三角形知识点总结及习题练习
解三角形一、基础知识梳理asinAsinBsinCb2Rc2R=b=c=2R(R为△ABC外接圆半径),了解正弦定理以下变形:a?…
-
解三角形知识点归纳
一正弦定理(一)知识与工具:abc???2R。正弦定理:在△ABC中,sinAsinBsinC在这个式子当中,已知两边和一角或已知…
-
高中数学必修五 第一章 解三角形知识点归纳及测试卷
高中数学必修五第一章解三角形知识点归纳1、三角形三角关系:A+B+C=180;C=180(A+B);2、三角形三边关系:a+b>c…
-
高考高中物理学史归纳总结1
高考高中物理学史归纳总结1、1638并在比萨斜塔做了两个不同质量的小球下落的实验,推翻了古希腊学者亚里士多德的观点2、16xx年,…