解直角三角形知识点总结
解直角三角形 济宁学院附属中学
直角三角形的性质
 1、直角三角形的两个锐角互余
1、直角三角形的两个锐角互余
几何表示:∵∠C=90°∴∠A+∠B=90°
2、在直角三角形中,30°角所对的直角边等于斜边的一半。
几何表示:∵∠C=90°∠A=30°∴BC= AB
AB
3、直角三角形斜边上的中线等于斜边的一半
几何表示:∵∠ACB=90° D为AB的中点 ∴ CD= AB=BD=AD
AB=BD=AD
4、勾股定理: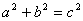
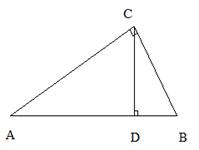 5、射影定理:在直角三角形中,斜边上的高线是两直角边在斜边上的射影的比例中项,每条直角边是它们在斜边上的射影和斜边的比例中项
5、射影定理:在直角三角形中,斜边上的高线是两直角边在斜边上的射影的比例中项,每条直角边是它们在斜边上的射影和斜边的比例中项
∵∠ACB=90°CD⊥AB
∴ 


6、常用关系式
由三角形面积公式可得:AB CD=AC
CD=AC BC
BC
锐角三角函数的概念
如图,在△ABC中,∠C=90°


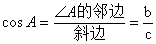
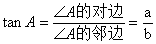

锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数
锐角三角函数的取值范围:0≤sinα≤1,0≤cosα≤1,tanα≥0,cotα≥0.
锐角三角函数之间的关系
(1)平方关系

(2)倒数关系
tanA tan(90°—A)=1
tan(90°—A)=1
(3)弦切关系
tanA= cotA=
cotA=
(4)互余关系
sinA=cos(90°—A),cosA=sin(90°—A)
tanA=cot(90°—A),cotA=tan(90°—A)
特殊角的三角函数值

说明:锐角三角函数的增减性,当角度在0°~90°之间变化时.
(1)正弦值随着角度的增大(或减小)而增大(或减小)
(2)余弦值随着角度的增大(或减小)而减小(或增大)
(3)正切值随着角度的增大(或减小)而增大(或减小)
(4)余切值随着角度的增大(或减小)而减小(或增大)
解直角三角形的概念
 在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。解直角三角形的理论依据:以上.
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。解直角三角形的理论依据:以上.
对实际问题的处理
(1)俯、仰角.
(2)方位角、象限角.
(3)坡角、坡度.
补充:在两个直角三角形中,都缺解直角三角形的条件时,可用列方程的办法解决。
有关公式
(1) =
= =
=
(2)Rt△面积公式:
(3)结论:直角三角形斜边上的高
(4)测底部不可到达物体的高度.如右图,
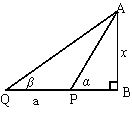 在Rt△ABP中,
在Rt△ABP中,
BP=xcotα
在Rt△AQB中,
BQ=xcotβ
BQ—BP=a,
即xcotβ-xcotα=a.
解直角三角形的知识的应用,可以解决:
(1)测量物体高度.
(2)有关航行问题.
(3)计算坝体或边路的坡度等问题
第二篇:解三角形知识点小结
解三角形知识点小结
一、知识梳理
1.形如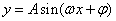 的函数:
的函数:
(1)几个物理量:A—振幅;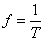 —频率(周期的倒数);
—频率(周期的倒数);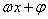 —相位;
—相位;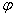 —初相;
—初相;
(2)函数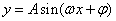 表达式的确定:A由最值确定;
表达式的确定:A由最值确定;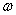 由周期确定;
由周期确定;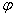 由图象上的特殊点确定,
由图象上的特殊点确定,
(3)函数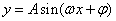 图象的画法:①“五点法”——设
图象的画法:①“五点法”——设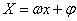 ,令
,令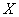 =0,
=0, 求出相应的
求出相应的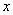 值,计算得出五点的坐标,描点后得出图象;②图象变换法:
值,计算得出五点的坐标,描点后得出图象;②图象变换法:
(4)函数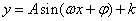 的图象与
的图象与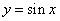 图象间的关系:若由
图象间的关系:若由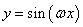 得到
得到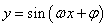 的图象,则向左或向右平移应平移
的图象,则向左或向右平移应平移 个单位,如(1)函数
个单位,如(1)函数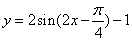 的图象经过怎样的变换才能得到
的图象经过怎样的变换才能得到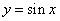 的图象?(答:
的图象?(答: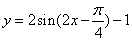 向上平移1个单位得
向上平移1个单位得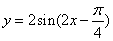 的图象,再向左平移
的图象,再向左平移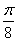 个单位得
个单位得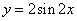 的图象,横坐标扩大到原来的2倍得
的图象,横坐标扩大到原来的2倍得 的图象,最后将纵坐标缩小到原来的
的图象,最后将纵坐标缩小到原来的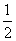 即得
即得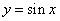 的图象);(2) 要得到函数
的图象);(2) 要得到函数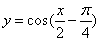 的图象,只需把函数
的图象,只需把函数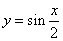 的图象向___平移____个单位(答:左;
的图象向___平移____个单位(答:左;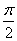 );(3)将函数
);(3)将函数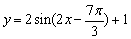 图像,按向量
图像,按向量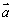 平移后得到的函数图像关于原点对称,这样的向量是否唯一?若唯一,求出
平移后得到的函数图像关于原点对称,这样的向量是否唯一?若唯一,求出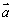 ;若不唯一,求出模最小的向量(答:存在但不唯一,模最小的向量
;若不唯一,求出模最小的向量(答:存在但不唯一,模最小的向量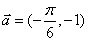 );(4)若函数
);(4)若函数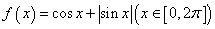 的图象与直线
的图象与直线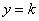 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则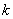 的取值范围是 (答:
的取值范围是 (答: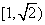 )
)
(5)研究函数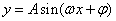 性质的方法:类比于研究
性质的方法:类比于研究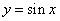 的性质,只需将
的性质,只需将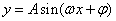 中的
中的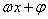 看成
看成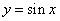 中的
中的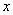 ,但在求
,但在求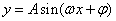 的单调区间时,要特别注意A和
的单调区间时,要特别注意A和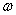 的符号,通过诱导公式先将
的符号,通过诱导公式先将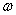 化正。
化正。
(1)函数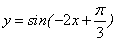 的递减区间是______(答:
的递减区间是______(答: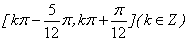 );
);
(2)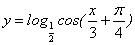 的递减区间是_______(答:
的递减区间是_______(答: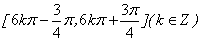 );
);
(3)(4)(5)函数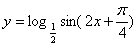 的单调减区间为( )
的单调减区间为( )
A 
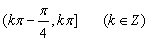 B
B 
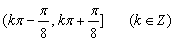
C 
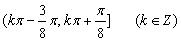 2.正弦定理:在一个三角形中,各边和它的所对角的正弦的比相等.
2.正弦定理:在一个三角形中,各边和它的所对角的正弦的比相等.
形式一: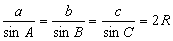 (解三角形的重要工具)
(解三角形的重要工具)
形式二: (边化正弦)
(边化正弦)
形式三: (比的性质)
(比的性质)
形式四: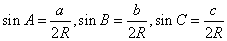 (正弦化边)
(正弦化边)
3.余弦定理:三角形任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍..
形式一: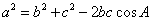
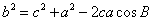 (遇见二次想余弦)
(遇见二次想余弦)
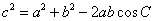
形式二: 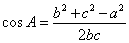 ,
,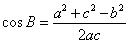 ,
,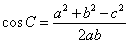
二、经典例题
问题一:利用正弦定理解三角形
【例1】在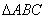 中,若
中,若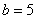 ,
,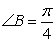 ,
,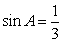 ,则
,则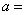 .
.
【例2】在△ABC中,已知a=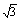 ,b=
,b=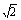 ,B=45°,求A、C和c.
,B=45°,求A、C和c.
问题二:利用余弦定理解三角形
【例3】设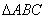 的内角
的内角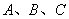 所对的边分别为
所对的边分别为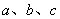 .已知
.已知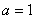 ,
,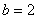 ,
,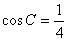 .
.
(Ⅰ)求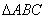 的周长,(Ⅱ)求
的周长,(Ⅱ)求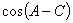 的值.
的值.
【例4】设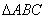 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3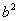 +3
+3 -3
-3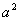 =4
=4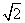 bc .
bc .
(Ⅰ) 求sinA的值;(Ⅱ)求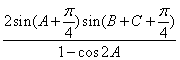 的值.
的值.
练习:在△ABC中,a、b、c分别是角A,B,C的对边,且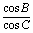 =-
=-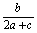 .
.
(1) 求角B的大小;(2)若b=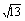 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
问题三:正弦定理余弦定理综合应用
【例5】在 ABC中,内角A,B,C的对边分别为a,b,c.已知
ABC中,内角A,B,C的对边分别为a,b,c.已知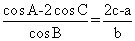 .
.
(I) 求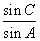 的值;(II)若cosB=
的值;(II)若cosB=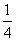 ,
,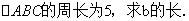
【例6】在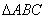 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为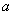 、
、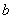 、
、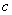 ,已知
,已知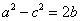 ,且
,且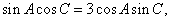 求b
求b 

练习:在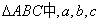 分别为内角A、B、C的对边,且
分别为内角A、B、C的对边,且
(Ⅰ)求角A的大小;(Ⅱ)若 ,试判断
,试判断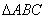 的形状。
的形状。
问题四:三角恒等变形
【例7】△ 中,
中,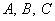 所对的边分别为
所对的边分别为 ,
, ,
, .(1)求
.(1)求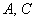 ;(2)若
;(2)若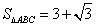 ,求
,求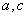 .
.
问题五:判断三角形形状
【例8】在△ABC中,,bcosA=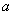 cosB,试判断
cosB,试判断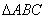 三角形的形状.
三角形的形状.
【例9】 在△ABC中,若=,试判断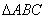 三角形的形状.
三角形的形状.
练习1.在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是
2.在△ABC中,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断三角形的形状.
问题六:与其他知识综合
【例10】已知向量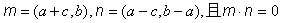 ,其中A,B,C是△ABC的内角,a,b,c分别是角A,B,C的对边
,其中A,B,C是△ABC的内角,a,b,c分别是角A,B,C的对边 .(1)求角C的大小;(2)求
.(1)求角C的大小;(2)求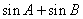 的取值范围.
的取值范围.
练习:在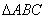 中,角
中,角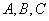 所对的边分别为
所对的边分别为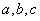 ,且满足
,且满足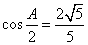 ,
,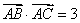 . (I)求
. (I)求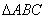 的面积; (II)若
的面积; (II)若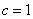 ,求
,求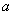 的值.
的值.
问题7:三角实际应用
 【例11】.(2007山东)20(本小题满分12分)如图,甲船以每小时
【例11】.(2007山东)20(本小题满分12分)如图,甲船以每小时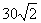 海里
海里
的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于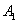 处
处
时,乙船位于甲船的北偏西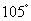 的方向
的方向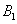 处,此时两船相距20海里.当甲
处,此时两船相距20海里.当甲
船航行20分钟到达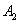 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西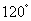 方
方
向的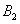 处,此时两船相距
处,此时两船相距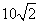 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
三、课后跟踪训练
1.若△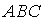 的三个内角满足
的三个内角满足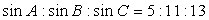 ,则△
,则△ ( )
( )
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
2.在△ABC中,内角A,B,C的对边分别是a,b,c,若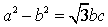 ,
,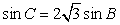 ,则A=( ) (A)
,则A=( ) (A)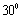 (B)
(B)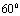 (C)
(C)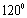 (D)
(D)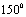
3.在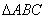 中,a=15,b=10,A=60°,则
中,a=15,b=10,A=60°,则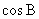 =
=
A -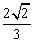 B
B 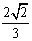 C -
C -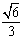 D
D 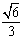
4.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=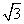 , A+C=2B, 则sinC= .
, A+C=2B, 则sinC= .
5在锐角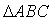 中,
中,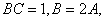 则
则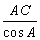 的值等于 ,
的值等于 , 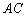 的取值范围为 .
的取值范围为 .
6.在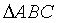 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为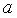 、
、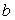 、
、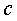 ,已知
,已知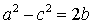 ,且
,且
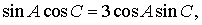 求b
求b 

7.在△ABC中,已知A、B、C成等差数列,求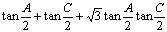 的值。
的值。
8.在 中,
中,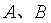 为锐角,角
为锐角,角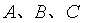 所对的边分别为
所对的边分别为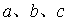 ,且
,且
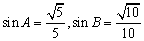 (I)求
(I)求 的值;(II)若
的值;(II)若 ,求
,求 的值。
的值。 

9.在△ABC中,已知B=45°,D是BC边上的一点AD=10,AC=14,DC=6,求AB的长.
10.在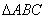 中,
中, 分别为内角
分别为内角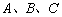 的对边,
的对边,
且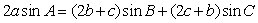
(Ⅰ)求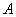 的大小;
的大小;
(Ⅱ)若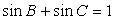 ,试判断
,试判断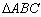 的形状.
的形状.
11. 在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求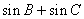 的最大值.
的最大值.
-
高一数学解三角形知识点总结及习题练习
解三角形一、基础知识梳理asinAsinBsinCb2Rc2R=b=c=2R(R为△ABC外接圆半径),了解正弦定理以下变形:a?…
-
解三角形知识点总结及典型例题
课前复习两角和与差的正弦、余弦、正切公式1两角和与差的正弦公式,sin(α+β)=sinαcosβ+cosαsinβ,sin(α-…
-
高中数学必修5__解三角形知识点总结与练习
解三角形一、知识点总结1.内角和定理:在?ABC中,A?B?C??;sin(A?B)?sinC;cos(A?B)??cosC;si…
-
必修5 解三角形知识点归纳总结
第一章解三角形一.正弦定理:1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即2.变形:1)a…
-
解三角形知识点归纳
一正弦定理(一)知识与工具:abc???2R。正弦定理:在△ABC中,sinAsinBsinC在这个式子当中,已知两边和一角或已知…
-
初二数学上全等三角形知识点总结很全
全等三角形知识梳理一、知识网络??对应角相等性质???对应边相等???边边边SSS??全等形?全等三角形?边角边SAS?应用??判…
-
相似三角形知识点总结及习题
相似三角形基本知识(一)比例的性质1.比例的基本性质:比例式化积、积化比例式.ac??ad?bcbd2.合、分比性质:分子加(减)…
-
全等三角形知识点总结
定义能够完全重合的两个三角形称为全等三角形。(注:全等三角形是相似三角形中的特殊情况)当两个三角形完全重合时,互相重合的顶点叫做对…
-
三角形知识点总结
第一章图形的初步认识考点一、线段垂直平分线,角的平分线,垂线1、线段垂直平分线的性质定理及逆定理垂直于一条线段并且平分这条线段的直…
-
三角形知识点总结(完)
三角形1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL(Rt△≌Rt△)2…
-
教育教学基本素质和能力知识点总结
1、教学技能的观点:活动方式说,行为说,结构说,能力说,知识说;2、教学技能:教学技能是教师在已有的知识经验基础上,通过实践练习和…