高中数学数列知识点总结
n
数列通项an与前n项和Sn的关系
?S1
1.Sn?a1?a2?a3???an??ai 2.an??
i?1?Sn?Sn?1
n?1n?2
第一部分 等差数列 一 定义式: an?an?1?d
??am?(n?m)d
二 通项公式:an?
?a?(n?1)d?1
一个数列是等差数列的等价条件:an?an?b(a,b为常数),即an是
关于n的一次函数,因为n?Z,所以an关于n的图像是一次函数图像的分点表示形式。 三 前n项和公式: Sn?
n(a1?an)n(n?1)
?na1?d 22
一个数列是等差数列的另一个充要条件:Sn?an2?bn?c(a,b,c为常
数,a≠0),即Sn是关于n的二次函数,因为n?Z,所以Sn关于n的图像是二次函数图像的分点表示形式。
四 性质结论1. a与b的等差中项A?a?b;
2
2. 在等差数列?an?中,若m?n?p?q,则
am?an?ap?aq;若m?n?2p,则am?an?2ap; 3. Sn,S2n?Sn,S3n?S2n仍成等差数列.
第二部分 等比数列 一 定义:
an
?q(n?2,an?0,q?0)?{a}n成等比数列。 an?1
n?1n?m
二 通项公式:an?a1q,an?amq
(q?1)?na1
?
三 前n项和:Sn??a1(1?qn)a1?an?1q;
?(q?1)?1?q1?q?
四 性质结论:1.a与b的等比中项
G?G2?ab?G?(a,b同号);
2.在等比数列?an?中,若m?n?p?q,则am?an?ap?aq;
若m?n?2p,则am?an?ap2;
?仍成等比数列。 4. q??1时,Sn,S2n?Sn,S3n?S2n,
1
第三部分 递推数列求通项公式 类型1 an?1?an?f(n) (累加法)
解法:把原递推公式转化为an?1?an?f(n),利用累加法求解。 例:已知数列?an?满足a1?,an?1?an?n,求an。 类型2 an?1?f(n)an (累乘法) 解法:把原递推公式转化为
23
an?1
?f(n),利用累乘法求解。 an
12
例:已知数列?an?满足a1?,an?1?
n
an,求an。 n?1
类型3 an?1?pan?q(其中p,q均为常数)。(辅助数列法) 例:已知数列?an?中,a1?1,an?1?2an?3,求an.
类型4 递推公式为Sn与an的关系式。(或Sn?f(an)) (Sn法) 解法:这种类型一般利用an??
?S1????????????????(n?1)
与
?Sn?Sn?1???????(n?2)
例:已知数列?an?前n项和Sn?n2?4n?1,求通项公式an. 第四部分 求前n项和Sn
一 直接法:即直接用等差、等比数列的求和公式求和。 (1)等差数列的求和公式:Sn?
n(a1?an)n(n?1)
?na1?d 22
?na1(q?1)n
(2)等比数列的求和公式Sn?? ?a1(1?q)(q?1)(切记:公比要讨论)
??1?q
二 裂项相消法: 求数列?
?
1?
?的前n项和,其中?an?是等差数列。 ?anan?1?
三 错位相减法:求数列?anbn?的前n项和,其中?an?是等差数列,?bn?是
等比数列。
?bn?是四 分组求和法:求数列?an?bn?的前n项和,其中?an?是等差数列,
等比数列。
2
第二篇:高中数学数列知识点总结
数列
一、数列定义:
数列是按照一定次序排列的一列数,是定义在正整数集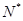 (或它的有限子集
(或它的有限子集 )上的函数
)上的函数 ,当自变量从1开始由小到大依次取正整数时,相对应的一列函数值为
,当自变量从1开始由小到大依次取正整数时,相对应的一列函数值为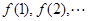 ; 通常用
; 通常用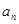 代替
代替 ,于是数列的一般形式常记为
,于是数列的一般形式常记为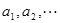 或简记为
或简记为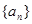 ,其中
,其中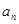 表示数列
表示数列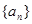 的通项。
的通项。
注意:(1)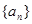 与
与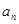 是不同的概念,
是不同的概念,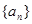 表示数列
表示数列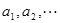 ,而
,而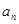 表示的是数列的第
表示的是数列的第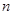 项;
项;
(2)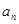 和
和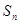 之间的关系:
之间的关系: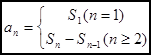
二、等差数列、等比数列的性质:

三、判定方法:
(1)等差数列的判定方法:
①定义法: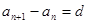 或
或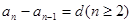 (
(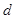 为常数)
为常数)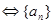 是等差数列
是等差数列
②中项公式法: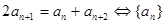 是等差数列
是等差数列
③通项公式法: (
(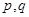 为常数)
为常数)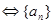 是等差数列
是等差数列
④前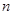 项和公式法:
项和公式法: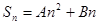 (
(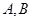 为常数)
为常数)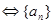 是等差数列
是等差数列
(2)等比数列的判定方法:
①定义法: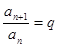 或
或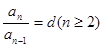 (
(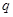 是不为零的常数)
是不为零的常数)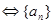 是等比数列
是等比数列
②中项公式法: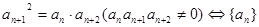 是等差数列
是等差数列
③通项公式法: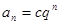 (
(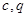 是不为零常数)
是不为零常数)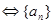 是等差数列
是等差数列
④前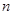 项和公式法:
项和公式法: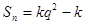 (
(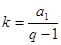 是常数)
是常数) 是等差数列
是等差数列
四、数列的通项求法:
(1)观察法:如:(1)0.2,0.22,0.222,……(2)21,203,2005,20007,……
(2)化归法:通过对递推公式的变换转化成等差数列或等比数列。
①递推式为 及
及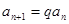 (
( 为常数):直接运用等差(比)数列。
为常数):直接运用等差(比)数列。
②递推式为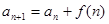 :迭加法
:迭加法
如:已知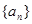 中
中 ,
,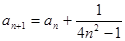 ,求
,求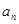
③递推式为 :迭乘法
:迭乘法
如:已知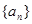 中
中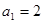 ,
, ,求
,求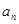
④递推式为 (
(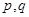 为常数):
为常数):
构造法:Ⅰ、由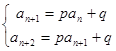 相减得
相减得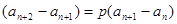 ,则
,则
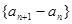 为等比数列。
为等比数列。
Ⅱ、设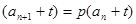 ,得到
,得到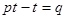 ,
, ,则
,则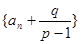 为等比数列。
为等比数列。
如:已知 ,求
,求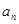
⑤递推式为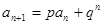 (
(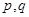 为常数):
为常数):
两边同时除去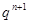 得
得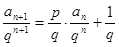 ,令
,令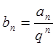 ,转化为
,转化为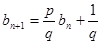 ,再用④法解决。
,再用④法解决。
如:已知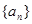 中,
中,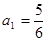 ,
,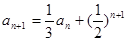 ,求
,求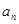
⑥递推式为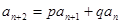 (
(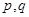 为常数):
为常数):
将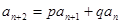 变形为
变形为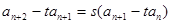 ,可得出
,可得出 解出
解出 ,于是
,于是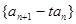 是公比为
是公比为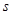 的等比数列。
的等比数列。
如:已知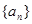 中,
中,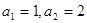 ,
, ,求
,求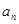
(3)公式法:运用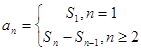
①已知 ,求
,求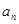 ;②已知
;②已知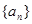 中,
中, 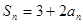 ,求
,求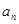 ;
;
③已知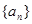 中,
中, ,求
,求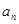
五、数列的求和法:
(1)公式法:
①等差(比)数列前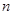 项和公式:②
项和公式:②
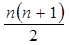 ;
;
③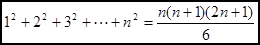 ;④
;④
(2)倒序相加(乘)法:
如:①求和: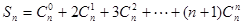 ;
;
②已知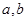 为不相等的两个正数,若在
为不相等的两个正数,若在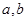 之间插入
之间插入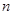 个正数,使它们构成以
个正数,使它们构成以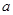 为首项,
为首项,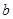 为末项的等比数列,求插入的这
为末项的等比数列,求插入的这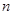 个正数的积
个正数的积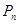 ;
;
(3)错位相减法:如:求和: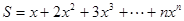
(4)裂项相消法: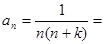 ;
;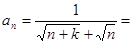 ;
;
如:①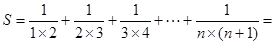 ;
;
②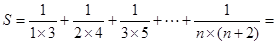 ;
;
③若 ,则
,则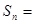 ;
;
(5)并项法:如:求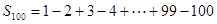
(6)拆项组合法:如:在数列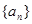 中,
中,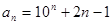 ,求
,求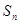 ,
,
六、数列问题的解题的策略:
分类讨论问题:
① 在等比数列中,用前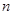 项和公式时,要对公比
项和公式时,要对公比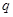 进行讨论;只有
进行讨论;只有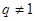 时才能用前
时才能用前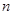 项和公式,
项和公式,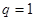 时
时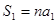
②已知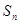 求
求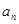 时,要对
时,要对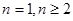 进行讨论;最后看
进行讨论;最后看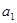 满足不满足
满足不满足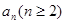 ,若满足
,若满足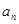 中的
中的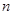 扩展到
扩展到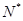 ,不满足分段写成
,不满足分段写成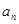 www.ks5u.com
www.ks5u.com
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
高中数学数列知识点总结(精华版)
小小亲清辅导班一数列1数列的定义按照一定顺序排列的一列数称为数列数列中的每个数称为该数列的项数列中的数是按一定次序排列的在这里只强…
-
高中数学知识点总结与题库(数列)
第六章数列二重难点击本章重点数列的概念等差数列等比数列的定义通项公式和前n项和公式及运用等差数列等比数列的有关性质注重提炼一些重要…
-
高中数学数列知识点总结
五数列一数列定义数列是按照一定次序排列的一列数那么它就必定有开头的数有相继的第二个数有第三个数于是数列中的每一个数都对应一个序号反…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1等差数列的定义与性质定义an1andd为常数ana1n1d等差中项xAy成等差数列2Axy前n项和Sna…
-
等差数列知识点总结
等差数列1.定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数…
-
等差数列知识点总结1111111111
等差数列1.定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数…
-
等差数列知识点总结
等差数列知识清单1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,…
-
高中数学数列知识点总结
数列一、数列定义:数列是按照一定次序排列的一列数,是定义在正整数集N(或它的有限子集*{1,2,3,?,n})上的函数f(n),当…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
初三化学第一单元知识点总结
第1单元走进化学世界化学是研究物质的组成、结构、性质以及变化规律的基础科学。2、我国劳动人民商代会制造青铜器,春秋战国时会炼铁、炼…