【原创】递推数列求和公式分类总结
递推数列分类解析
(1) an?1=an+f(n)类型————逐差法
例:an?1= an+n-2,a1=1,求通项公式。
2
答案:an=(n-5n+6)/2
(2) an?1=f(n)*an-----------------逐商法
例:已知a1=1,an= a1+2a2+3a3+……+(n-1)an?1(n≥2) 则an=﹛1,n=1
___,n≥2 [04全国Ⅰ]
解: 由已知得,an?1= a1+2a2+3a3+……+(n-1)an?1+n an 与上式相减得
n≥2时,an?1- an=n an即an?1=(n+1) an
又a1=1 , a2/a1=1, a3/ a2=3, a4/ a3=4,……, an/ an?1=n 以上各式相乘得
an=1*1*2*3*4*%*……*n=n!/2(n>=2)
(3) an?1=p an+q(p≠1,q≠0)----------待定系数法构造等比数列 即令an?1+λ=p(an+λ),与已知式对比系数
(4)Sn=f(an)
一般利用an=S1(n=1); Sn-Sn?1(n≥2)
(5)* an?1=pan+r*q( p≠1,0,q≠0,r≠0)
当p≠q时,一般用待定系数法构造等比数列,即令an?1+λq
nn?1n=p(an+λq) n对比系数得λ(p-q)=r,即λ=r、(p-q)转化为{ an+ q *r/(p-q)}为等比数列;当p=q时,
an?1=p an+r q,将递推式两边同时除以qnn?1,得an?1/ qn?1= an/ q+r/q,从而转化为{ an/ n
q}是等差数列
例:Sn=3/4* an-1/3*2^(n+1)+3/2,n=1,2,3,……求数列{ an}的通项。【06全国Ⅰ】 解:当n=1时,S1= a1=3/4* a1-1/3*4+2/3 得a1=2
n≥2时,Sn- Sn?1= an=4/3* an-4/3 an?1-1/3*2^(n+1)+1/3*2^n
化简得an=4 an?1+2^n ○1
设an+λ*2^n=4(an?1+λ*2^(n-1))即an=4 an?1+λ2^n,与○1式比较得,λ=1 ∴an+2^n=4(an?1+2^n)
∴{an+2^n}是以4为首项、4为公比的等比数列
∴2^n+an=4^n an=4^n-2^n
(6) an?1=pan+a*n+b (p≠1,0,a≠0)
一般用待定系数法构造等比数列,即令an?1+x(n+1)+y=p(an+xn+y) 与已知式比较,解出x,y,转化为{an+xn+y}是以p为公比的等比数列 例:{an}中a1=1/2,点(n, 2an?1-an)在直线y=x上,其中n=1,2,3,……求an【06山东】 解:∵2an?1-an=n,
∴an?1=1/2*an+n/2
所以令an?1+x(n+1)+y=1/2(an+xn+y)
an?1=1/2*an-x/2*n-x-1/2*y,与○1式比较得
x=-1,y=2
∴an?1-(n+1)+2=1/2(an-n),又a1=1/2
所以{an-n=2}是以3/2为首项,1/2为公比的等比数列
所以 -n+2+an=3/2*(1/2)^(n-1)=3/(2^n)
∴
an=3/(2^n)+n-2 n
(7) an?1=p*ar
n(p>0, an>0)
两边取对数后转化为类型(3)
例:已知an>0,a0=1,an?1=1/2 *an(4- an),n∈N【05江西】
(1) 证明:an<an?1<2,.n∈N
(2) 求an
(1) 证明:略(用数学归纳法并结合f(x)=1/2*x(4-x)单调性证明)
(2) 解:因为an?1=1/2an(3-an)=-1/2(an-2)^2+2
所以 2-an?1=1/2(2-an)^2
由(1)知2-an>0,
所以 log2
令bn= log2(2- an?1)=-1+2 log2(2- an) (2- an)则bn?1=-1+2 bn
所以bn?1-1=2(bn-1)
故{ bn-1}是以2为公比的等比数列
得bn=1-2^n= log2(2- an)
所以 an=2-2^(1-2^n)
(8) an?1={f(n)* an}/(g(n) an+h(n))
两边取倒数后转化为类型(3)
(9)an?2=p an?1+q an
一般利用an?2-αan?1=β(an?1-αan)构造等比数列
例:【06福建】已知a1=1,a2=3,an?2
-2 an,求数列的通项。
=3 an?1
(10) an?1=(p an+q)/(r an+m)【特征方程】
当特征方程x=(px+q)/(rx+m)有两个不同的根x1与x2时,{ (an-x1)/( an-x2)}是等比数列;当它仅有一根x0时,{1/(an-x0)}是等差数列
例【05重庆】已知a1=1,8 an?1*an-16 an?1+2 an+5=0求an
(11)周期型:找出周期
(12)an+ an?1=pn+q或an* an?1=p*q^n
一般转化为{a2n?1}与{a2n}是等差或等比数列
(13)归纳猜想法
【06全国Ⅱ】
设{ an}的前n项和为Sn,且方程x^2- anx]- an=0有一根为Sn-1,n=1,2,……
(1) 求a1 ,a2
(2) 求通项
第二篇:【原创】递推数列求和公式分类总结
递推数列分类解析
(1) an?1=an+f(n)类型————逐差法
例:an?1= an+n-2,a1=1,求通项公式。
2
答案:an=(n-5n+6)/2
(2) an?1=f(n)*an-----------------逐商法
例:已知a1=1,an= a1+2a2+3a3+……+(n-1)an?1(n≥2)
则an=﹛1,n=1
___,n≥2 [04全国Ⅰ]
解: 由已知得,an?1= a1+2a2+3a3+……+(n-1)an?1+n an
与上式相减得
n≥2时,an?1- an=n an即an?1=(n+1) an
又a1=1 , a2/a1=1, a3/ a2=3, a4/ a3=4,……, an/ an?1=n
以上各式相乘得
an=1*1*2*3*4*%*……*n=n!/2(n>=2)
(3) an?1=p an+q(p≠1,q≠0)----------待定系数法构造等比数列 即令an?1+λ=p(an+λ),与已知式对比系数
(4)Sn=f(an)
一般利用an=S1(n=1); Sn-Sn?1(n≥2)
(5)* an?1=pan+r*q( p≠1,0,q≠0,r≠0)
当p≠q时,一般用待定系数法构造等比数列,即令an?1+λq
nn?1n=p(an+λq) n对比系数得λ(p-q)=r,即λ=r、(p-q)转化为{ an+ q *r/(p-q)}为等比数列;当p=q时,
an?1=p an+r q,将递推式两边同时除以qnn?1,得an?1/ qn?1= an/ q+r/q,从而转化为{ an/ n
q}是等差数列
例:Sn=3/4* an-1/3*2^(n+1)+3/2,n=1,2,3,……求数列{ an}的通项。【06全国Ⅰ】 解:当n=1时,S1= a1=3/4* a1-1/3*4+2/3 得a1=2
n≥2时,Sn- Sn?1= an=4/3* an-4/3 an?1-1/3*2^(n+1)+1/3*2^n
化简得an=4 an?1+2^n ○1
设an+λ*2^n=4(an?1+λ*2^(n-1))即an=4 an?1+λ2^n,与○1式比较得,λ=1
∴an+2^n=4(an?1+2^n)
∴{an+2^n}是以4为首项、4为公比的等比数列
∴2^n+an=4^n an=4^n-2^n
(6) an?1=pan+a*n+b (p≠1,0,a≠0)
一般用待定系数法构造等比数列,即令an?1+x(n+1)+y=p(an+xn+y)
与已知式比较,解出x,y,转化为{an+xn+y}是以p为公比的等比数列
例:{an}中a1=1/2,点(n, 2an?1-an)在直线y=x上,其中n=1,2,3,……求an【06山东】 解:∵2an?1-an=n,
∴an?1=1/2*an+n/2
所以令an?1+x(n+1)+y=1/2(an+xn+y)
an?1=1/2*an-x/2*n-x-1/2*y,与○1式比较得
x=-1,y=2
∴an?1-(n+1)+2=1/2(an-n),又a1=1/2
所以{an-n=2}是以3/2为首项,1/2为公比的等比数列
所以 -n+2+an=3/2*(1/2)^(n-1)=3/(2^n)
∴
an=3/(2^n)+n-2 n
(7) an?1=p*ar
n(p>0, an>0)
两边取对数后转化为类型(3)
例:已知an>0,a0=1,an?1=1/2 *an(4- an),n∈N【05江西】
(1) 证明:an<an?1<2,.n∈N
(2) 求an
(1) 证明:略(用数学归纳法并结合f(x)=1/2*x(4-x)单调性证明)
(2) 解:因为an?1=1/2an(3-an)=-1/2(an-2)^2+2
所以 2-an?1=1/2(2-an)^2
由(1)知2-an>0,
所以 log2
令bn= log2(2- an?1)=-1+2 log2(2- an) (2- an)则bn?1=-1+2 bn
所以bn?1-1=2(bn-1)
故{ bn-1}是以2为公比的等比数列
得bn=1-2^n= log2(2- an)
所以 an=2-2^(1-2^n)
(8) an?1={f(n)* an}/(g(n) an+h(n))
两边取倒数后转化为类型(3)
(9)an?2=p an?1+q an
一般利用an?2-αan?1=β(an?1-αan)构造等比数列
例:已知a1=1,a2=3,an?2
-2 an,求数列的通项。
=3 an?1
(10) an?1=(p an+q)/(r an+m)【特征方程】
当特征方程x=(px+q)/(rx+m)有两个不同的根x1与x2时,{ (an-x1)/( an-x2)}是等比数列;当它仅有一根x0时,{1/(an-x0)}是等差数列
例已知a1=1,8 an?1*an-16 an?1+2 an+5=0求an
(11)周期型:找出周期
(12)an+ an?1=pn+q或an* an?1=p*q^n
一般转化为{a2n?1}与{a2n}是等差或等比数列
(13)归纳猜想法
设{ an}的前n项和为Sn,且方程x^2- anx]- an=0有一根为Sn-1,n=1,2,……
(1) 求a1 ,a2
(2) 求通项
画图分情况讨论
(1)a>0时,f(x)与x轴的两个交点为0,-1,开口向上,最低点为
(-1/2,-a/4),画出图像,g(x)的图像为y=x向右移动a个单位,此时x=-1/2时,g(x)=-1/2-a,所以f(x)和g(x)没有交点,此种情况舍去。
(2)a<0时,f(x)与x轴的两个交点为0,-1,开口向下,最高点为
(-1/2,-a/4),画出图像,g(x)的图像仍为y=x向右移动a个单位,与f(x)交点为p,q,其中一个大于0,一个小于0,由题意知p>0,从图上可以看出,x属于(0,p)时,g(x)图像在f(x)下方,所以g(x)《f(x),又此时a<0,p>0,p-a>0,而f(x)《0,所以有g(x)《f(x)《p-a
第三篇:数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数 列
数列的考查主要涉及数列的基本公式、基本性质、通项公式,递推公式、数列求和、数列极限、简单的数列不等式证明等.
1.数列的有关概念:
(1) 数列:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项.
(2) 从函数的观点看,数列可以看做是一个定义域为正整数集 (或它的有限子集)的函数。当自变量从小到大依次取值时对应的一列函数值。由于自变量的值是离散的,所以数列的值是一群孤立的点。
(或它的有限子集)的函数。当自变量从小到大依次取值时对应的一列函数值。由于自变量的值是离散的,所以数列的值是一群孤立的点。
(3) 通项公式:如果数列 的第
的第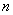 项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即
项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即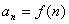 .如:
.如:  。
。
(4) 递推公式:如果已知数列 的第一项(或前几项),且任何一项
的第一项(或前几项),且任何一项 与它的前一项
与它的前一项 (或前几项)间的关系可以用一个式子来表示,即
(或前几项)间的关系可以用一个式子来表示,即 或
或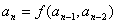 ,那么这个式子叫做数列
,那么这个式子叫做数列 的递推公式. 如数列
的递推公式. 如数列 中,
中, ,其中
,其中 是数列
是数列 的递推公式.再如:
的递推公式.再如: 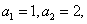
 。
。
2.数列的表示方法:
(1) 列举法:如1,3,5,7,9,… (2)图象法:用(n, an)孤立点表示。
(3) 解析法:用通项公式表示。 (4)递推法:用递推公式表示。
 3.数列的分类:
3.数列的分类:
按有界性
4.数列{an}及前n项和之间的关系:

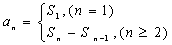
等差数列
1.等差数列的概念
如果一个数列从第二项起,每一项与它前一项的差等于同一个常数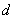 ,这个数列叫做等差数列,常数
,这个数列叫做等差数列,常数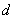 称为等差数列的公差.
称为等差数列的公差.
2.通项公式与前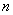 项和公式
项和公式
⑴通项公式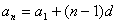 ,
,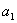 为首项,
为首项,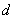 为公差.可变形为
为公差.可变形为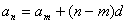
⑵前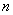 项和公式
项和公式 或
或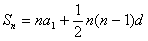 .
.
3.等差中项
如果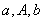 成等差数列,那么
成等差数列,那么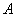 叫做
叫做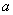 与
与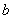 的等差中项.
的等差中项.
即: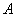 是
是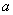 与
与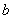 的等差中项
的等差中项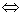
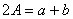
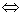
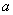 ,
,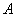 ,
,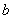 成等差数列.
成等差数列.
4.等差数列的判定方法
⑴定义法: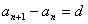 (
( ,
,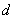 是常数)
是常数)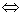
 是等差数列;
是等差数列;
⑵中项法: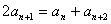 (
( )
)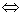
 是等差数列.
是等差数列.
5.常用性质: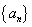 是等差数列
是等差数列
(1)若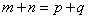 ,则
,则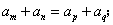
(2)数列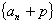 、
、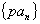 (
(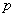 是常数)都是等差数列;在等差数列
是常数)都是等差数列;在等差数列 中,等距离取出若干项也构成一个等差数列,即
中,等距离取出若干项也构成一个等差数列,即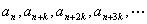 为等差数列,公差为
为等差数列,公差为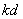 。
。
(3) 仍为等差数列,公差为
仍为等差数列,公差为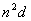 ;
;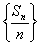 是等差数列。
是等差数列。
(4)若三个成等差数列,可设为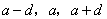 ;四个数成等差数列,可设为
;四个数成等差数列,可设为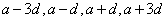
(5)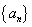 为等差数列
为等差数列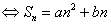 (
(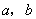 为常数,是关于
为常数,是关于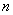 的常数项为0的二次函数)。(
的常数项为0的二次函数)。(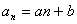 (
(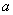 ,
,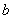 是常数))
是常数))
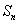 的最值可求二次函数
的最值可求二次函数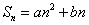 的最值;或者求出
的最值;或者求出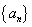 中的正、负分界项,
中的正、负分界项,
即:当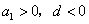 ,解不等式组
,解不等式组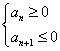 可得
可得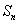 达到最大值时的
达到最大值时的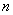 值.
值.
当 ,由
,由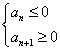 可得
可得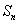 达到最小值时的
达到最小值时的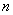 值.
值.
(6) 项数为偶数 的等差数列
的等差数列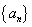 ,有
,有
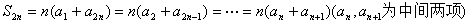
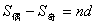 ,
, .
.
(7)项数为奇数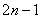 的等差数列
的等差数列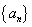 ,有
,有
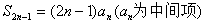 ,
,
 ,
,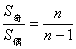 .
.
等比数列
1.等比数列的概念
如果一个数列从第二项起,每一项与它前一项的比等于同一个常数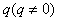 ,这个数列叫做等比数列,常数
,这个数列叫做等比数列,常数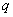 称为等比数列的公比.
称为等比数列的公比.
2.通项公式与前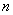 项和公式
项和公式
⑴通项公式: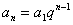 ,
,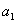 为首项,
为首项,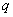 为公比 . 可变形为
为公比 . 可变形为
⑵前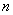 项和公式:①当
项和公式:①当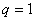 时,
时,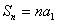
②当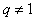 时,
时,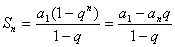 .
.
3.等比中项
如果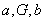 成等比数列,那么
成等比数列,那么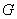 叫做
叫做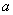 与
与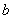 的等比中项.
的等比中项.
即: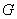 是
是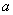 与
与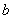 的等比中项
的等比中项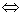
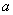 ,
,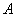 ,
,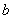 成等比数列
成等比数列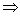
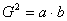 .
.
4.等比数列的判定方法
⑴定义法: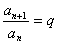 (
( ,
,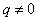 是常数)
是常数)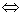
 是等比数列;
是等比数列;
⑵中项法: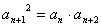 (
( )且
)且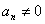
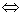
 是等比数列.
是等比数列.
5.常用性质
⑴数列 是等比数列,则数列
是等比数列,则数列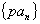 是等比数列;等距离取出若干项也构成一个等比数列,即
是等比数列;等距离取出若干项也构成一个等比数列,即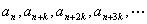 为等比数列,公比为
为等比数列,公比为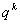 ;
; 仍为等比数列,公比为
仍为等比数列,公比为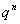 .
.
⑵若 ,则
,则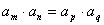 ;
;
⑶如果三个数构成等比数列,则设其为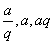 ;若四个数成等比数列,则可设其为
;若四个数成等比数列,则可设其为 。
。
⑷等比数列的通项公式可以改写成 。当
。当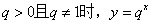 是一个指数函数,而
是一个指数函数,而 是一个不为0的常数与指数函数的积。
是一个不为0的常数与指数函数的积。
通项公式,数列求和
一、求数列通项公式
1)给出递推公式求通项公式
1°递推关系形如" ,
, 是可求和的。可利用迭加法或迭代法:
是可求和的。可利用迭加法或迭代法: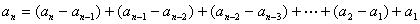
例1:已知数列 中,
中,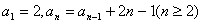 ,求数列
,求数列 的通项公式;
的通项公式;
例2:已知数列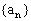 满足
满足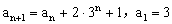 ,求数列
,求数列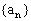 的通项公式。
的通项公式。
2°递推关系形如"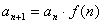 ,
, 是可求积的。可利用迭乘法:
是可求积的。可利用迭乘法: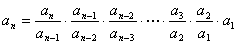
例1:数列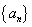 中,
中,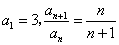 ,求
,求
例2:已知数列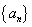 满足:
满足: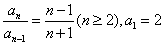 ,求数列
,求数列 的通项公式;
的通项公式;
例3:已知数列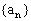 满足
满足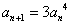 ,
, ,求数列
,求数列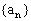 的通项公式。
的通项公式。
3°递推关系形如“ ”,可利用待定系数法:可把它变为
”,可利用待定系数法:可把它变为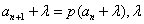 为待定系数。令
为待定系数。令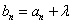 ,先求数列
,先求数列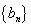 的通项公式,进而求
的通项公式,进而求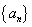 的通项公式。
的通项公式。
例1:已知数列 中,
中,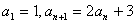 ,求数列
,求数列 的通项公式.
的通项公式.
例2: 已知数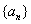 的递推关系为
的递推关系为 ,且
,且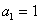 求通项
求通项 。
。
4°递推关系形如“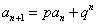 ”,两边同除以
”,两边同除以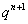 (
(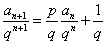 )并采用待定系数法求解或者直接采用待定系数法(
)并采用待定系数法求解或者直接采用待定系数法(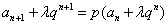 )。
)。
例1. 已知数列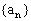 满足
满足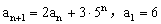 ,求数列
,求数列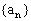 的通项公式。
的通项公式。
例2. 已知数列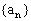 满足
满足 ,求数列
,求数列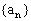 的通项公式。
的通项公式。
5°递推已知数列 中,关系形如“
中,关系形如“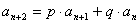 ”,利用待定系数法求解(
”,利用待定系数法求解( )
)
例1:已知数列 中,
中,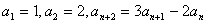 ,求数列
,求数列 的通项公式.
的通项公式.
例2:在数列 中,
中,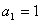 ,
,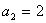 ,
, ,求
,求 。
。
6°递推关系形如"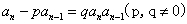 ,两边同除以
,两边同除以 (
(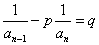 )
)
例1:已知数列 中,
中,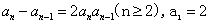 ,求数列
,求数列 的通项公式.
的通项公式.
例2:数列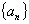 中,
中,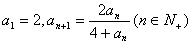 ,求数列
,求数列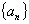 的通项公式.
的通项公式.
2)给出前n项和求通项公式
例1:⑴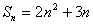 ; ⑵
; ⑵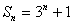 .
.
3)、给出关于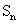 和
和 的关系
的关系
例1:数列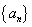 满足
满足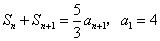 ,求
,求
例2:设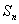 是数列
是数列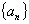 的前
的前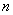 项和,
项和,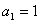 ,
,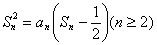 .求
.求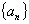 的通项
的通项
例3:已知数列 中,
中,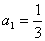 ,前
,前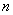 项和
项和 与
与 的关系是
的关系是  ,试求通项公式
,试求通项公式 。
。
例4:已知数列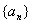 的前
的前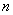 项和为
项和为 ,且满足
,且满足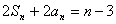
 .求数列
.求数列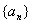 的通项公式。
的通项公式。
二. 求数列前n项和的常用方法
1)公式法:直接由等差,等比数列的求和公式求和,注意等比时q=1和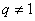 的讨论。
的讨论。
等差数列求和公式: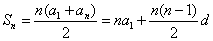
等比数列求和公式:
例1: 已知 ,求
,求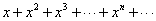 的前n项和.
的前n项和.
例2: 设Sn=1+2+3+…+n,n∈N*,求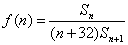 的最大值.
的最大值.
2)拆项求和法: 通过拆分、合并、分组,将所求和转化为等差、等比数列求和
例1:求和:2×5+3×6+4×7+…+n(n+3)
例2:求数列的前n项和: ,…
,…
例3:求数列 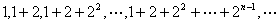 的前
的前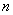 项和
项和
例4:求数列{n(n+1)(2n+1)}的前n项和.
3)倒序相加法:如果一个数列与首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前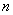 项和即可用倒序相加法
项和即可用倒序相加法
把数列的各项顺序倒写,再与原来顺序的数列相加.
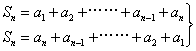 相加
相加

例1: 求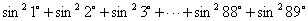 的值
的值
例2:如已知函数f(x)对任意x∈R都有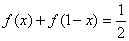 ,
,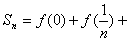
 +…
+…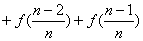
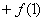 ,(
,(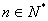 ),求
),求
例3:设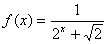 ,求
,求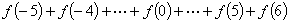 的值
的值
例4:已知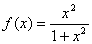 ,
,
那么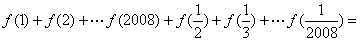 _____
_____
4)裂项相消法
把数列各项拆成两项或多项之和,使之出现成对互为相反数的项. 数列的常见拆项有: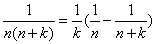 ;
;

例1:在数列{an}中,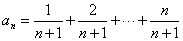 ,又
,又 ,求数列{bn}的前n项的和.
,求数列{bn}的前n项的和.
例2:求和:S=1+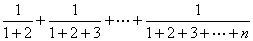
例3:求和: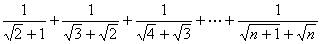 .
.
5)错位相减法
若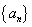 为等差数列,
为等差数列,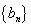 为等比数列,求数列
为等比数列,求数列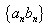 (差比数列)前
(差比数列)前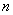 项和,可由
项和,可由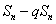 ,求
,求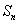 ,其中
,其中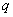 为
为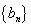 的公比.
的公比.
例1:求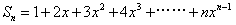
例2:若数列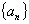 的通项
的通项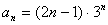 ,求此数列的前
,求此数列的前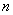 项和
项和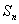 .
.
例3: 求数列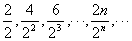 前n项的和.
前n项的和.
常用的公式:
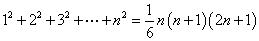
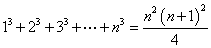
-
数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数列数列的考查主要涉及数列的基本公式基本性质通项公式递推公式数列求和数列极限简单的数列不等式证明等1数列的有关概念1数列按照一定顺…
-
数列求和常用公式
数列求和常用公式1123nnn122122232n2nn12n163132333n3123n2n2n1244122334nn1nn…
-
数列通项公式和求和公式总结
【一】求数列通项公式的常用方法各个求通项的方法之间并不是相互孤立的,有时同一题目中也可能同时用到几种方法,要具体问题具体分析!一公…
-
数列求和方法总结
数列求和方法总结朱亚芬数列求和是中学数学中一个十分有趣的课题它对于加深巩固中学数学课程的学习开拓中学生的知识领域都十分有益这个开阔…
-
【原创】递推数列求和公式分类总结
递推数列分类解析(1)an?1=an+f(n)类型————逐差法例:an?1=an+n-2,a1=1,求通项公式。2答案:an=(…
-
数列通项公式和求和公式总结
【一】求数列通项公式的常用方法各个求通项的方法之间并不是相互孤立的,有时同一题目中也可能同时用到几种方法,要具体问题具体分析!一公…
-
求数列前n项和及通项公式的若干方法及总结
求数列前n项和一.公式法:利用下列常用求和公式求和是数列求和的最基本最重要的方法。(1)等差:Sn?n(a1?an)?na1?n(…
-
数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数列数列的考查主要涉及数列的基本公式基本性质通项公式递推公式数列求和数列极限简单的数列不等式证明等1数列的有关概念1数列按照一定顺…
-
求数列通项公式方法总结(附答案)
求数列通项公式的常用方法1公式法2由Sn求ann1时a1S1n2时anSnSn13求差商法111a12a2nan2n512221解…
-
数列求和与求通项公式方法总结(已打)
一公式法即直接用等差等比数列的求和公式求和1等差数列的求和公式Sn2等比数列的求和公式Sn例1求和1123n2222232n二分组…
-
数列求和方法总结
数列求和的基本方法和技巧数列是高中代数的重要内容,又是学习高等数学的基础。在高考和各种数学竞赛中都占有重要的地位。数列求和是数列的…