求数列通项公式方法总结(附答案)
求数列通项公式的常用方法:
1、公式法
2、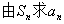
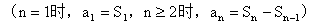
3、求差(商)法
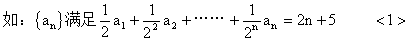
解: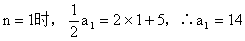
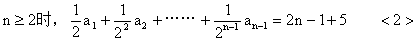
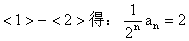
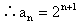
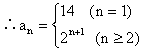
[练习]
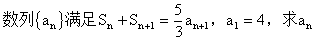
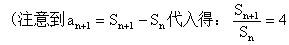

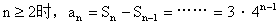
4、叠乘法
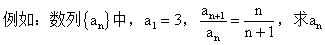
解: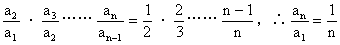
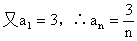
5、等差型递推公式
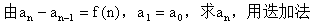
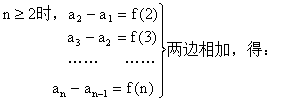
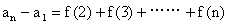
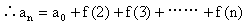
[练习]
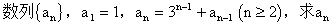
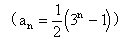
6、等比型递推公式


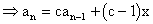



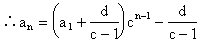
[练习]
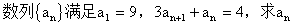

7、倒数法




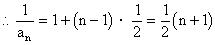

2.数列求和问题的方法
(1)、应用公式法
等差、等比数列可直接利用等差、等比数列的前n项和公式求和,另外记住以下公式对求和来说是有益的。
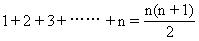
1+3+5+……+(2n-1)=n2
(2)、分解转化法
对通项进行分解、组合,转化为等差数列或等比数列求和。
【例9】求和S=1·(n2-1)+ 2·(n2-22)+3·(n2-32)+…+n(n2-n2)
解 S=n2(1+2+3+…+n)-(13+23+33+…+n3)
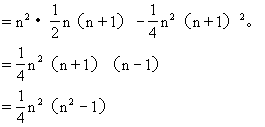
(3)、倒序相加法
适用于给定式子中与首末两项之和具有典型的规律的数列,采取把正着写与倒着写的两个和式相加,然后求和。
例10、求和:
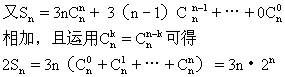 例10、解
例10、解 
∴ Sn=3n·2n-1
(4)、错位相减法
如果一个数列是由一个等差数列与一个等比数列对应项相乘构成的,可把和式的两端同乘以上面的等比数列的公比,然后错位相减求和.
例11、 求数列1,3x,5x2,…,(2n-1)xn-1前n项的和.
解 设Sn=1+3+5x2+…+(2n-1)xn-1. ①
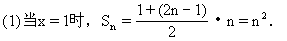
(2)x=0时,Sn=1.
(3)当x≠0且x≠1时,在式①两边同乘以x得 xSn=x+3x2+5x3+…+(2n-1)xn,②
①-②,得 (1-x)Sn=1+2x+2x2+2x3+…+2xn-1-(2n-1)xn.
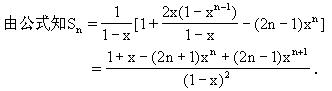
(5)裂项法:
把通项公式整理成两项(式多项)差的形式,然后前后相消。
常见裂项方法:
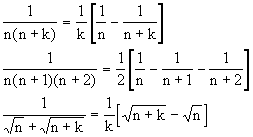
例12、求和

注:在消项时一定注意消去了哪些项,还剩下哪些项,一般地剩下的正项与负项一样多。
在掌握常见题型的解法的同时,也要注重数学思想在解决数列问题时的应用。
求通项公式
(1)观察法。(2)由递推公式求通项。
对于由递推公式所确定的数列的求解,通常可通过对递推公式的变换转化成等差数列或等比数列问题。
(1)递推式为an+1=an+d及an+1=qan(d,q为常数)
例1、 已知{an}满足an+1=an+2,而且a1=1。求an。
例1、解 ∵an+1-an=2为常数 ∴{an}是首项为1,公差为2的等差数列
∴an=1+2(n-1) 即an=2n-1
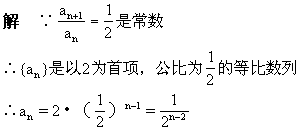 例2、已知
例2、已知 满足
满足 ,而
,而 ,求
,求 =?
=?
(2)递推式为an+1=an+f(n)
例3、已知 中
中 ,
, ,求
,求 .
.
解: 由已知可知

令n=1,2,…,(n-1),代入得(n-1)个等式累加,即(a2-a1)+(a3-a2)+…+(an-an-1)
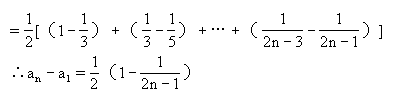
★ 说明 只要和f(1)+f(2)+…+f(n-1)是可求的,就可以由an+1=an+f(n)以n=1,2,…,(n-1)代入,可得n-1个等式累加而求an。
(3)递推式为an+1=pan+q(p,q为常数)
例4、 中,
中, ,对于n>1(n∈N)有
,对于n>1(n∈N)有 ,求
,求 .
.
解法一: 由已知递推式得an+1=3an+2,an=3an-1+2。两式相减:an+1-an=3(an-an-1)
因此数列{an+1-an}是公比为3的等比数列,其首项为a2-a1=(3×1+2)-1=4
∴an+1-an=4·3n-1 ∵an+1=3an+2 ∴3an+2-an=4·3n-1 即 an=2·3n-1-1
解法二: 上法得{an+1-an}是公比为3的等比数列,于是有:a2-a1=4,a3-a2=4·3,a4-a3=4·32,…,an-an-1=4·3n-2,

把n-1个等式累加得: ∴an=2·3n-1-1
(4)递推式为an+1=p an+q n(p,q为常数)


 由上题的解法,得:
由上题的解法,得: ∴
∴

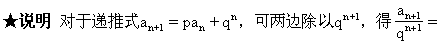
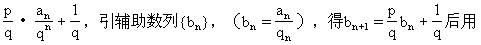
(5)递推式为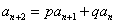
思路:设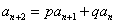 ,可以变形为:
,可以变形为: ,
,
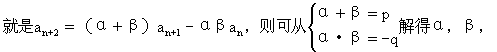 想
想
于是{an+1-αan}是公比为β的等比数列,就转化为前面的类型。
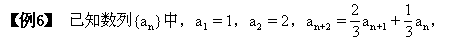 求
求 。
。

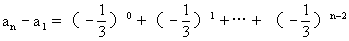
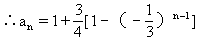
(6)递推式为Sn与an的关系式
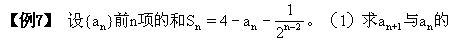
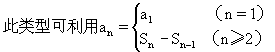
关系;(2)试用n表示an。

∴
∴ ∴
∴
上式两边同乘以2n+1得2n+1an+1=2nan+2则{2nan}是公差为2的等差数列。
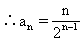 ∴2nan= 2+(n-1)·2=2n
∴2nan= 2+(n-1)·2=2n
等差数列前 项和的最值问题:
项和的最值问题:
1、若等差数列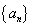 的首项
的首项 ,公差
,公差 ,则前
,则前 项和
项和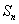 有最大值。
有最大值。
(ⅰ)若已知通项 ,则
,则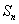 最大
最大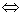
 ;
;
(ⅱ)若已知 ,则当
,则当 取最靠近
取最靠近 的非零自然数时
的非零自然数时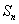 最大;
最大;
2、若等差数列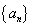 的首项
的首项 ,公差
,公差 ,则前
,则前 项和
项和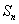 有最小值
有最小值
(ⅰ)若已知通项 ,则
,则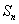 最小
最小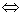
 ;
;
(ⅱ)若已知 ,则当
,则当 取最靠近
取最靠近 的非零自然数时
的非零自然数时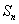 最小。
最小。
第二篇:根据数列递推公式求其通项公式方法总结
根据数列递推公式求其通项公式方法总结
已知数列的递推公式,求取其通项公式是数列中一类常见的题型,这类题型如果单纯的看某一个具体的题目,它的求解方法灵活是灵活多变的,构造的技巧性也很强,但是此类题目也有很强的规律性,存在着解决问题的通法,本文就高中数学中常见的几类题型从解决通法上做一总结,方便于学生学习和老师的教学,不涉及具体某一题目的独特解法与技巧。
一、 型数列,(其中
型数列,(其中 不是常值函数)
不是常值函数)
此类数列解决的办法是累加法,具体做法是将通项变形为 ,从而就有
,从而就有

将上述 个式子累加,变成
个式子累加,变成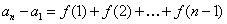 ,进而求解。
,进而求解。
例1. 在数列 中,
中,
解:依题意有

逐项累加有 ,从而
,从而 。
。
注:在运用累加法时,要特别注意项数,计算时项数容易出错.
类似题型练习:已知 满足
满足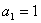 ,
, 求
求 的通项公式。
的通项公式。
二、 型数列,(其中
型数列,(其中 不是常值函数)
不是常值函数)
此类数列解决的办法是累积法,具体做法是将通项变形为 ,从而就有
,从而就有

将上述 个式子累乘,变成
个式子累乘,变成 ,进而求解。
,进而求解。
例2. 已知数列 中
中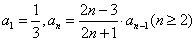 ,求数列
,求数列 的通项公式。
的通项公式。
解:当 时,
时, 将这
将这 个式子累乘,得到
个式子累乘,得到 ,从而
,从而 ,当
,当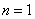 时,
时, ,所以
,所以 。
。
注:在运用累乘法时,还是要特别注意项数,计算时项数容易出错.
类似题型练习:在数列 中,
中,  >0,
>0, ,求
,求 .
.
提示:依题意分解因式可得 ,而
,而 >0,所以
>0,所以 ,即
,即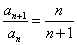 。
。
三、 型数列
型数列
此类数列解决的办法是将其构造成一个新的等比数列,再利用等比数列的性质进行求解,构造的办法有两种,一是待定系数法构造,设 ,展开整理
,展开整理 ,比较系数有
,比较系数有 ,所以
,所以 ,所以
,所以 是等比数列,公比为
是等比数列,公比为 ,首项为
,首项为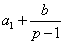 。二是用做差法直接构造,
。二是用做差法直接构造, ,
, ,两式相减有
,两式相减有 ,所以
,所以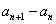 是公比为
是公比为 的等比数列。
的等比数列。
例3. 在数列 中,
中, ,当
,当 时,有
时,有 ,求
,求 的通项公式。
的通项公式。
解法1:设 ,即有
,即有 ,对比
,对比 ,得
,得 ,于是得
,于是得 ,数列
,数列 是以
是以 为首项,以3为公比的等比数列,所以有
为首项,以3为公比的等比数列,所以有 。
。
解法2:由已知递推式,得 ,上述两式相减,得
,上述两式相减,得 ,因此,数列
,因此,数列 是以
是以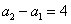 为首项,以3为公比的等比数列。所以
为首项,以3为公比的等比数列。所以 ,即
,即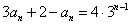 ,所以
,所以 。
。
类似题型练习:已知数列 满足
满足 求数列
求数列 的通项公式.
的通项公式.
注:根据题设特征恰当地构造辅助数列,利用基本数列可简捷地求出通项公式.
四. 型数列(p为常数)
型数列(p为常数)
此类数列可变形为 ,则
,则 可用累加法求出,由此求得
可用累加法求出,由此求得 .
.
例4已知数列 满足
满足 ,求
,求 .
.
解:将已知递推式两边同除以 得
得 ,设
,设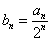 ,故有
,故有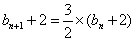 ,
,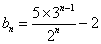 ,从而
,从而 .
.
注:通过变形,构造辅助数列,转化为基本数列的问题,是我们求解陌生的递推关系式的常用方法.
若 为
为 的一次函数,则
的一次函数,则 加上关于
加上关于 的一次函数构成一个等比数列; 若
的一次函数构成一个等比数列; 若 为
为 的二次函数, 则
的二次函数, 则 加上关于
加上关于 的二次函数构成一个等比数列.这时我们用待定系数法来求解.
的二次函数构成一个等比数列.这时我们用待定系数法来求解.
例5.已知数列 满足
满足
解:作 ,则
,则 ,
, 代入已知递推式中得:
代入已知递推式中得: .
.
令

这时 且
且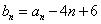
显然,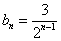 ,所以
,所以 .
.
注:通过引入一些待定系数来转化命题结构,经过变形和比较,把问题转化成基本数列,从而使问题得以解决.
类似题型练习:
(1)已知 满足
满足 ,求
,求 。
。
(2)已知数列 ,
, 表示其前
表示其前 项和,若满足
项和,若满足 ,求数列
,求数列 的通项公式。
的通项公式。
提示:(2)中利用 ,把已知条件转化成递推式。
,把已知条件转化成递推式。
五、 型数列(
型数列( 为非零常数)
为非零常数)
这种类型的解法是将式子两边同时取倒数,把数列的倒数看成是一个新数列,便可顺利地转化为 型数列。
型数列。
例6.已知数列 满足
满足 ,求
,求 .
.
解:两边取倒数得: ,所以
,所以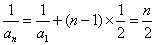 ,故有
,故有 。
。
类似题型练习:数列 中,
中, ,求
,求 的通项。
的通项。
六.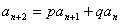 型数列(
型数列( 为常数)
为常数)
这种类型的做法是用待定糸数法设 构造等比数列。
构造等比数列。
例5.数列 中,
中, 且
且 ,求
,求 .
.
解法略。
-
求数列通项公式方法经典总结
求数列通项公式方法1公式法定义法根据等差数列等比数列的定义求通项例1已知等差数列an满足a37a5a726求an2已知数列an满足…
-
求数列通项公式方法总结
等差数列对于一个数列an如果任意相邻两项之差为一个常数那么该数列为等差数列且称这一定值差为公差记为d从第一项a1到第n项an的总和…
-
求数列通项公式方法总结(附答案)
求数列通项公式的常用方法:1、公式法2、3、求差(商)法解:[练习]4、叠乘法解:5、等差型递推公式[练习]6、等比型递推公式[练…
-
求数列的通项公式方法总结
数列常见题型总结题型四求数列的通项公式一公式法当题中已知数列是等差数列或等比数列在求其通项公式时我们就可以直接利用等差或等比数列的…
-
根据递推公式,求数列通项公式的常用方法 总结归纳
求递推数列通项公式的常用方法归纳目录一概述二等差数列通项公式和前n项和公式1等差数列通项公式的推导过程2等差数列前n项和公式的推导…
-
求数列通项公式an的常用方法
专题:求数列通项公式an的常用方法一.递推数列求通项问题一.观察法已知数列前若干项,求该数列的通项时,一般对所给的项观察分析,寻找…
-
求数列前n项和及通项公式的若干方法及总结
求数列前n项和一.公式法:利用下列常用求和公式求和是数列求和的最基本最重要的方法。(1)等差:Sn?n(a1?an)?na1?n(…
-
数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数列数列的考查主要涉及数列的基本公式基本性质通项公式递推公式数列求和数列极限简单的数列不等式证明等1数列的有关概念1数列按照一定顺…
- 20xx江苏高考数列通项公式 方法总结
-
数列通项公式解法总结及习题(附详解答案)
数列通项公式解法总结及习题训练附答案1定义法等差数列通项公式等比数列通项公式2公式法已知Sn即a1a2anfn求an用作差法anS…
-
【原创】递推数列求和公式分类总结
递推数列分类解析(1)an?1=an+f(n)类型————逐差法例:an?1=an+n-2,a1=1,求通项公式。2答案:an=(…