求数列通项公式an的常用方法
专题:求数列通项公式 的常用方法
的常用方法
一.递推数列求通项问题
一. 观察法
已知数列前若干项,求该数列的通项时,一般对所给的项观察分析,寻找规律,从而
根据规律写出此数列的一个通项。
例1 已知数列 写出此数列的一个通项公式。
写出此数列的一个通项公式。
解 观察数列前若干项可得通项公式为
二、公式法
1 运用等差(等比)数列的通项公式.
2 已知数列 前
前 项和
项和 ,则
,则 (注意:不能忘记讨论
(注意:不能忘记讨论 )
)
例2 已知数列{an}的前n和 满足
满足 求此数列的通项公式。
求此数列的通项公式。
解得 ,当
,当
所以
三. (
( 可以求和)
可以求和) 累加法
累加法
例3、在数列 中,已知
中,已知 =1,当
=1,当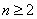 时,有
时,有
 ,求数列的通项公式。
,求数列的通项公式。
解析:
 上述
上述 个等式相加可得:
个等式相加可得:

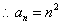
练习:1、已知数列 ,
, =2,
=2, =
= +3
+3 +2,求
+2,求 。
。
2、 已知数列 满足
满足
 求通项公式
求通项公式
3、若数列的递推公式为 ,则求这个数列的通项公式
,则求这个数列的通项公式
4. 已知数列 满足
满足  且
且 ,则求这个数列的通项公式
,则求这个数列的通项公式
四. (
( 可以求积)
可以求积) 累积法
累积法
例4、在数列 中,已知
中,已知 有
有 ,(
,(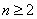 )求数列
)求数列 的通项公式。
的通项公式。
解析:原式可化为



又 也满足上式;
也满足上式;

练习:1、已知数列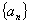 满足
满足 ,
, ,求
,求 。
。
2、已知 ,
,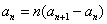
 ,求数列
,求数列 通项公式.
通项公式.
3、已知数列 满足
满足
 ,求通项公式
,求通项公式
五.
 待定常数法
待定常数法
可将其转化为 ,其中
,其中 ,则数列
,则数列 为公比等于A的等比数列,然后求
为公比等于A的等比数列,然后求 即可。
即可。
例5 在数列 中,
中,  ,当
,当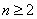 时,有
时,有 ,求数列
,求数列 的通项公式。
的通项公式。
解析:设 ,则
,则
 ,于是
,于是
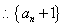 是以
是以 为首项,以3为公比的等比数列。
为首项,以3为公比的等比数列。
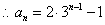
练习:1、在数列 中,
中,  ,
, ,求数列
,求数列 的通项公式。
的通项公式。
2、已知 ,
, ,求
,求 。
。
3、已知数列 满足
满足 ,求通项
,求通项
4.已知数列 满足
满足 ,求数列
,求数列 的通项公式。
的通项公式。
六. (
( )
) 倒数法
倒数法
例6 已知 ,
, ,求
,求 。
。
解析:两边取倒数得: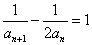 ,设
,设 则
则 ;
;
令 ;展开后得,
;展开后得, ;
; ;
;
 是以
是以 为首项,
为首项, 为公比的等比数列。
为公比的等比数列。
 ;即
;即 ,得
,得 ;
;
练习:1、设数列 满足
满足
 求
求
2、在数列 中,
中, ,求数列
,求数列 的通项公式.
的通项公式.
3、在数列 中,
中, ,求数列
,求数列 的通项公式.
的通项公式.
第二篇:求数列的通项公式的常用方法总结
求递推数列的通项公式的九种方法
利用递推数列求通项公式,在理论上和实践中均有较高的价值.自从二十世纪八十年代以来,这一直是全国高考和高中数学联赛的热点之一.
一、作差求和法
例1 在数列{ }中,
}中, ,
, ,求通项公式
,求通项公式 .
.
解:原递推式可化为: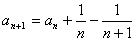
则

 ,……,
,……,
逐项相加得: .故
.故 .
.
二、作商求和法
例2 设数列{ }是首项为1的正项数列,且
}是首项为1的正项数列,且 (n=1,2,3…),则它的通项公式是
(n=1,2,3…),则它的通项公式是 =▁▁▁(20##年高考15题).
=▁▁▁(20##年高考15题).
解:原递推式可化为:
 =0
=0
∵  >0,
>0, 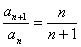
则  ……,
……,
逐项相乘得: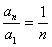 ,即
,即 =
= .
.
三、换元法
例3 已知数列{ },其中
},其中 ,且当n≥3时,
,且当n≥3时, ,求通项公式
,求通项公式 (1986年高考文科第八题改编).
(1986年高考文科第八题改编).
解:设 ,原递推式可化为:
,原递推式可化为:
 是一个等比数列,
是一个等比数列, ,公比为
,公比为 .故
.故 .
.
故 .由逐差法可得:
.由逐差法可得: .
.
例4已知数列{ },其中
},其中 ,且当n≥3时,
,且当n≥3时, ,求通项公式
,求通项公式 。
。
解 由 得:
得: ,令
,令 ,则上式为
,则上式为 ,因此
,因此 是一个等差数列,
是一个等差数列, ,公差为1.故
,公差为1.故 .。
.。
由于
又
所以 ,即
,即
四、积差相消法
例5(1993年全国数学联赛题一试第五题)设正数列 ,
, ,
, …,
…, ,…满足
,…满足
 =
=
 且
且 ,求
,求 的通项公式.
的通项公式.
解 将递推式两边同除以 整理得:
整理得:
设 =
=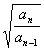 ,则
,则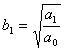 =1,
=1, ,故有
,故有
 ⑴
⑴
 ⑵
⑵
… … … …
 (
(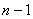 )
)
由⑴ + ⑵
+ ⑵ +…+(
+…+(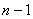 )
) 得
得 =
= ,即
,即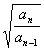 =
= .
.
逐项相乘得: =
=
 ,考虑到
,考虑到 ,
,
故 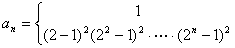
 .
.
五、取倒数法
例6 已知数列{ }中,其中
}中,其中 ,且当n≥2时,
,且当n≥2时,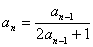 ,求通项公式
,求通项公式 。
。
解 将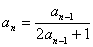 两边取倒数得:
两边取倒数得: ,这说明
,这说明 是一个等差数列,首项是
是一个等差数列,首项是 ,公差为2,所以
,公差为2,所以 ,即
,即 .
.
六、取对数法
例7 若数列{ }中,
}中, =3且
=3且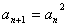 (n是正整数),则它的通项公式是
(n是正整数),则它的通项公式是 =▁▁▁(20##年上海高考题).
=▁▁▁(20##年上海高考题).
解 由题意知 >0,将
>0,将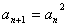 两边取对数得
两边取对数得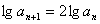 ,即
,即 ,所以数列
,所以数列 是以
是以 =
= 为首项,公比为2的等比数列,
为首项,公比为2的等比数列, ,即
,即 .
.
七、平方(开方)法
例8 若数列{ }中,
}中, =2且
=2且 (n
(n ),求它的通项公式是
),求它的通项公式是 .
.
解 将 两边平方整理得
两边平方整理得 。数列{
。数列{ }是以
}是以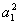 =4为首项,3为公差的等差数列。
=4为首项,3为公差的等差数列。 。因为
。因为 >0,所以
>0,所以 。
。
八、待定系数法
待定系数法解题的关键是从策略上规范一个递推式可变成为何种等比数列,可以少走弯路.其变换的基本形式如下:
1、 (A、B为常数)型,可化为
(A、B为常数)型,可化为 =A(
=A( )的形式.
)的形式.
例9 若数列{ }中,
}中, =1,
=1, 是数列{
是数列{ }的前
}的前 项之和,且
项之和,且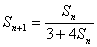 (n
(n ),求数列{
),求数列{ }的通项公式是
}的通项公式是 .
.
解 递推式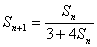 可变形为
可变形为 (1)
(1)
设(1)式可化为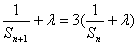 (2)
(2)
比较(1)式与(2)式的系数可得 ,则有
,则有 。故数列{
。故数列{ }是以
}是以 为首项,3为公比的等比数列。
为首项,3为公比的等比数列。 =
= 。所以
。所以 。
。
当n ,
, 。
。
数列{ }的通项公式是
}的通项公式是
 。
。
2、
 (A、B、C为常数,下同)型,可化为
(A、B、C为常数,下同)型,可化为 =
= )的形式.
)的形式.
例10 在数列{ }中,
}中, 求通项公式
求通项公式 。
。
解:原递推式可化为:
 ①
①
比较系数得 =-4,①式即是:
=-4,①式即是: .
.
则数列 是一个等比数列,其首项
是一个等比数列,其首项 ,公比是2.
,公比是2.
∴
即 .
.
3、 型,可化为
型,可化为 的形式。
的形式。
例11 在数列{ }中,
}中, ,当
,当 ,
, ① 求通项公式
① 求通项公式 .
.
解:①式可化为:

比较系数得 =-3或
=-3或 =-2,不妨取
=-2,不妨取 =-2.①式可化为:
=-2.①式可化为:

则 是一个等比数列,首项
是一个等比数列,首项 =2-2(-1)=4,公比为3.
=2-2(-1)=4,公比为3.
∴ .利用上题结果有:
.利用上题结果有:
 .
.
4、 型,可化为
型,可化为 的形式。
的形式。
例12 在数列{ }中,
}中, ,
, =6
=6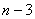 ①
①
求通项公式 .
.
解 ①式可化为:
 ② 比较系数可得:
② 比较系数可得:
 =-6,
=-6, ,② 式为
,② 式为
 是一个等比数列,首项
是一个等比数列,首项 ,公比为
,公比为 .
.
∴
即 
故 .
.
九、猜想法
运用猜想法解题的一般步骤是:首先利用所给的递推式求出 ……,然后猜想出满足递推式的一个通项公式
……,然后猜想出满足递推式的一个通项公式 ,最后用数学归纳法证明猜想是正确的。
,最后用数学归纳法证明猜想是正确的。
例13 在各项均为正数的数列 中,
中, 为数列
为数列 的前n项和,
的前n项和, =
= +
+  ,求其通项公式。
,求其通项公式。
-
求数列通项公式方法经典总结
求数列通项公式方法1公式法定义法根据等差数列等比数列的定义求通项例1已知等差数列an满足a37a5a726求an2已知数列an满足…
-
求数列通项公式方法总结
等差数列对于一个数列an如果任意相邻两项之差为一个常数那么该数列为等差数列且称这一定值差为公差记为d从第一项a1到第n项an的总和…
-
求数列通项公式方法总结(附答案)
求数列通项公式的常用方法:1、公式法2、3、求差(商)法解:[练习]4、叠乘法解:5、等差型递推公式[练习]6、等比型递推公式[练…
-
求数列的通项公式方法总结
数列常见题型总结题型四求数列的通项公式一公式法当题中已知数列是等差数列或等比数列在求其通项公式时我们就可以直接利用等差或等比数列的…
-
根据递推公式,求数列通项公式的常用方法 总结归纳
求递推数列通项公式的常用方法归纳目录一概述二等差数列通项公式和前n项和公式1等差数列通项公式的推导过程2等差数列前n项和公式的推导…
-
求数列前n项和及通项公式的若干方法及总结
求数列前n项和一.公式法:利用下列常用求和公式求和是数列求和的最基本最重要的方法。(1)等差:Sn?n(a1?an)?na1?n(…
-
数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数列数列的考查主要涉及数列的基本公式基本性质通项公式递推公式数列求和数列极限简单的数列不等式证明等1数列的有关概念1数列按照一定顺…
-
求数列通项公式方法总结(附答案)
求数列通项公式的常用方法:1、公式法2、3、求差(商)法解:[练习]4、叠乘法解:5、等差型递推公式[练习]6、等比型递推公式[练…
- 20xx江苏高考数列通项公式 方法总结
-
数列通项公式解法总结及习题(附详解答案)
数列通项公式解法总结及习题训练附答案1定义法等差数列通项公式等比数列通项公式2公式法已知Sn即a1a2anfn求an用作差法anS…