三角函数基础知识总结
自主招生讲座1—基础知识
1.定义1 角,一条射线绕着它的端点旋转得到的图形叫做角。若旋转方向为逆时针方向,则角为正角,若旋转方向为顺时针方向,则角为负角,若不旋转则为零角。角的大小是任意的。
2.定义2 角度制,把一周角360等分,每一等份为一度,弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。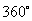 =2π rad。若圆心角的弧长为L,则其弧度数的绝对值|α|=
=2π rad。若圆心角的弧长为L,则其弧度数的绝对值|α|=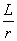 ,其中r是圆的半径(相应的扇形面积为
,其中r是圆的半径(相应的扇形面积为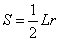 )。
)。
3.定义3 象限角:角的终边落在象限内的角,如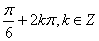 为第一象限角。
为第一象限角。
轴线角:角的终边落在坐标轴上的角,如终边落在 轴上的角的集合为:
轴上的角的集合为: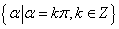
4.定义4 三角函数,在直角坐标平面内,把角α的顶点放在原点,始边与x轴的正半轴重合,在角的终边上任意取一个不同于原点的点P,设它的坐标为(x,y),到原点的距离为r,则正弦函数sin =
=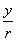 ,余弦函数cos
,余弦函数cos =
=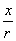 ,正切函数tan
,正切函数tan =
=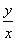 ,余切函数cot
,余切函数cot =
=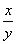 ,正割函数sec
,正割函数sec =
=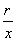 ,余割函数csc
,余割函数csc =
=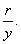 (在单位圆中定义更加简单)
(在单位圆中定义更加简单)
(1)三角函数的正否:“一全二正弦,三切四余弦”
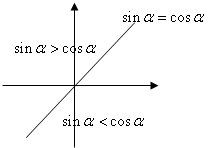 (2)
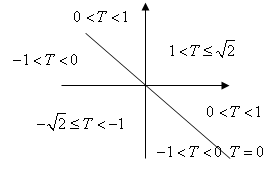
(2)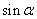 与
与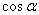 大小关系如图:
大小关系如图: 
(3)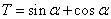 的大小范围如图:
的大小范围如图:
5.定义5 三角函数线:略
6.定理1 同角三角函数的基本关系式,倒数关系:tan =
=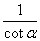 ,sin
,sin =
= ,cos
,cos =
=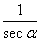 ;商数关系:tan
;商数关系:tan =
=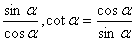 ;乘积关系:tan
;乘积关系:tan ×cos
×cos =sin
=sin ,cot
,cot ×sin
×sin =cos
=cos ;平方关系:sin2
;平方关系:sin2 +cos2
+cos2 =1, tan2
=1, tan2 +1=sec2
+1=sec2 , cot2
, cot2 +1=csc2
+1=csc2 ;若
;若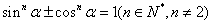 ,则
,则 为轴线角。
为轴线角。
7.定理2 诱导公式(Ⅰ)sin(α+π)=-sinα, cos(π+α)=-cosα, tan(π+α)=tanα, cot(π+α)=cotα;(Ⅱ)sin(-α)=-sinα, cos(-α)=cosα, tan(-α)=-tanα, cot(-α)=cotα; (Ⅲ)sin(π-α)=sinα, cos(π-α)=-cosα, tan=(π-α)=-tanα, cot(π-α)=-cotα; (Ⅳ)sin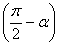 =cosα, cos
=cosα, cos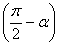 =sinα, tan
=sinα, tan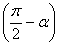 =cotα(奇变偶不变,符号看象限)。
=cotα(奇变偶不变,符号看象限)。
8.三角函数的图像:略(留意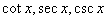 的图像)
的图像)
9.正弦函数的性质,根据图象可得y=sinx(x∈R)的性质如下。单调区间:在区间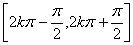 上为增函数,在区间
上为增函数,在区间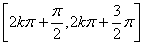 上为减函数,最小正周期为2
上为减函数,最小正周期为2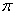 . 奇函数. 有界性:当且仅当x=2kx+
. 奇函数. 有界性:当且仅当x=2kx+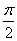 时,y取最大值1,当且仅当x=3k
时,y取最大值1,当且仅当x=3k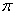 -
-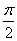 时, y取最小值-1。对称性:直线x=k
时, y取最小值-1。对称性:直线x=k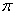 +
+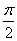 均为其对称轴,点(k
均为其对称轴,点(k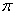 , 0)均为其对称中心,值域为[-1,1]。这里k∈Z.
, 0)均为其对称中心,值域为[-1,1]。这里k∈Z.
10.余弦函数的性质,根据图象可得y=cosx(x∈R)的性质。单调区间:在区间[2kπ, 2kπ+π]上单调递减,在区间[2kπ-π, 2kπ]上单调递增。最小正周期为2π。奇偶性:偶函数。对称性:直线x=kπ均为其对称轴,点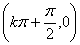 均为其对称中心。有界性:当且仅当x=2kπ时,y取最大值1;当且仅当x=2kπ-π时,y取最小值-1。值域为[-1,1]。这里k∈Z.
均为其对称中心。有界性:当且仅当x=2kπ时,y取最大值1;当且仅当x=2kπ-π时,y取最小值-1。值域为[-1,1]。这里k∈Z.
11.正切函数的性质:由图象知奇函数y=tanx(x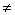 kπ+
kπ+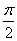 )在开区间(kπ-
)在开区间(kπ-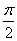 , kπ+
, kπ+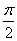 )上为增函数, 最小正周期为π,值域为(-∞,+∞),点(
)上为增函数, 最小正周期为π,值域为(-∞,+∞),点(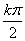 ,0)均为其对称中心。这里k∈Z.
,0)均为其对称中心。这里k∈Z.
12.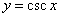 的性质:单调区间:增区间(
的性质:单调区间:增区间(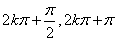 ),(
),(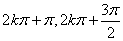 ),减区间(
),减区间(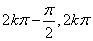 ),(
),(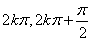 );最小正周期为2π,奇函数,对称轴为
);最小正周期为2π,奇函数,对称轴为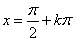 ,对称中心为
,对称中心为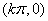 ,值域为
,值域为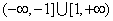 。这里k∈Z.
。这里k∈Z.
13. 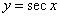 的性质:单调区间:增区间(
的性质:单调区间:增区间(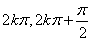 ),(
),(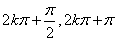 ),减区间(
),减区间(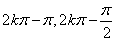 ),(
),(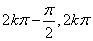 );最小正周期为2π,偶函数,对称轴为
);最小正周期为2π,偶函数,对称轴为 ,对称中心为
,对称中心为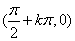 ,值域为
,值域为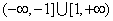 。这里k∈Z.
。这里k∈Z.
14.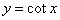 的性质:减区间为(
的性质:减区间为(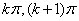 );最小正周期为π,奇函数,对称中心为
);最小正周期为π,奇函数,对称中心为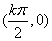 ,值域为R。这里k∈Z.
,值域为R。这里k∈Z.
15.平移与伸缩变换:(1)先平移后伸缩;(2)先伸缩后平移。图象之间的关系:y=sinx的图象经上下平移得y=sinx+k的图象;经左右平移得y=sin(x+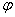 )的图象(相位变换);纵坐标不变,横坐标变为原来的
)的图象(相位变换);纵坐标不变,横坐标变为原来的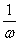 ,得到y=sin
,得到y=sin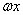 (
( )的图象(周期变换);横坐标不变,纵坐标变为原来的A倍,得到y=Asinx的图象(振幅变换);y=Asin(
)的图象(周期变换);横坐标不变,纵坐标变为原来的A倍,得到y=Asinx的图象(振幅变换);y=Asin(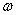 x+
x+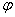 )(
)(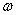 >0)的图象(周期变换);横坐标不变,纵坐标变为原来的A倍,得到y=Asinx的图象(振幅变换);y=Asin(
>0)的图象(周期变换);横坐标不变,纵坐标变为原来的A倍,得到y=Asinx的图象(振幅变换);y=Asin(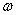 x+
x+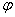 )(
)(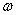 ,
, 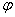 >0)(|A|叫作振幅)的图象向右平移
>0)(|A|叫作振幅)的图象向右平移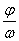 个单位得到y=Asin
个单位得到y=Asin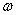 x的图象。
x的图象。
16.两角和与差的基本关系式:cos(α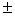 β)=cosαcosβ
β)=cosαcosβ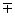 sinαsinβ,sin(α
sinαsinβ,sin(α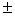 β)=sinαcosβ
β)=sinαcosβ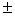 cosαsinβ; tan(α
cosαsinβ; tan(α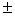 β)=
β)= (注意其的变形形式)
(注意其的变形形式)
17.和差化积与积化和差公式:(重要)
sinα+sinβ=2sin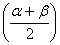 cos
cos ,sinα-sinβ=2sin
,sinα-sinβ=2sin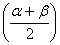 cos
cos ,
,
cosα+cosβ=2cos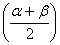 cos
cos , cosα-cosβ=-2sin
, cosα-cosβ=-2sin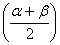 sin
sin ,
,
sinαcosβ=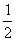 [sin(α+β)+sin(α-β)],cosαsinβ=
[sin(α+β)+sin(α-β)],cosαsinβ=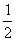 [sin(α+β)-sin(α-β)],
[sin(α+β)-sin(α-β)],
cosαcosβ=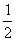 [cos(α+β)+cos(α-β)],sinαsinβ=-
[cos(α+β)+cos(α-β)],sinαsinβ=-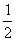 [cos(α+β)-cos(α-β)].
[cos(α+β)-cos(α-β)].
18.倍角公式:sin2α=2sinαcosα, cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α, tan2α=
19.三倍角公式: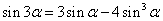 =
=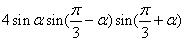
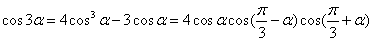
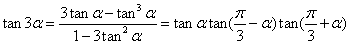
20.半角公式:sin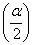 =
=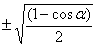 ,cos
,cos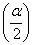 =
=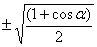 ,
,
tan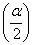 =
=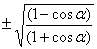 =
=
21.万能公式:  ,
, 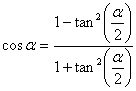 ,
,

22.辅助角公式:如果a, b是实数且a2+b2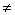 0,则取始边在x轴正半轴,终边经过点(a, b)的一个角为β,则sinβ=
0,则取始边在x轴正半轴,终边经过点(a, b)的一个角为β,则sinβ=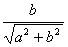 ,cosβ=
,cosβ=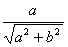 ,对任意的角α.
,对任意的角α.
asinα+bcosα=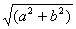 sin(α+β).
sin(α+β).
23.正弦定理:在任意△ABC中有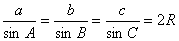 ,其中a, b, c分别是角A,B,C的对边,R为△ABC外接圆半径。
,其中a, b, c分别是角A,B,C的对边,R为△ABC外接圆半径。
24.余弦定理:在任意△ABC中有a2=b2+c2-2bcosA,其中a,b,c分别是角A,B,C的对边。
25.在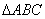 中,下列公式成立:
中,下列公式成立:
(1)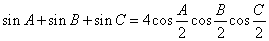
(2)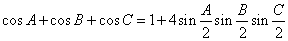
(3)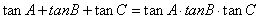
(4)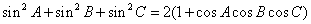
(4)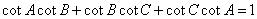
(5)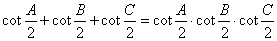
(6)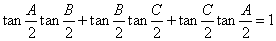
26.函数y=sinx 的反函数叫反正弦函数,记作y=arcsinx(x∈[-1, 1]),函数y=cosx(x∈[0, π]) 的反函数叫反余弦函数,记作y=arccosx(x∈[-1, 1]). 函数y=tanx
的反函数叫反正弦函数,记作y=arcsinx(x∈[-1, 1]),函数y=cosx(x∈[0, π]) 的反函数叫反余弦函数,记作y=arccosx(x∈[-1, 1]). 函数y=tanx 的反函数叫反正切函数。记作y=arctanx(x∈[-∞, +∞]). y=cosx(x∈[0, π])的反函数称为反余切函数,记作y=arccotx(x∈[-∞, +∞]).
的反函数叫反正切函数。记作y=arctanx(x∈[-∞, +∞]). y=cosx(x∈[0, π])的反函数称为反余切函数,记作y=arccotx(x∈[-∞, +∞]).
定理15 三角方程的解集,如果a∈(-1,1),方程sinx=a的解集是{x|x=nπ+(-1)narcsina, n∈Z}。方程cosx=a的解集是{x|x=2kx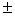 arccosa, k∈Z}. 如果a∈R,方程tanx=a的解集是{x|x=kπ+arctana, k∈Z}。恒等式:arcsina+arccosa=
arccosa, k∈Z}. 如果a∈R,方程tanx=a的解集是{x|x=kπ+arctana, k∈Z}。恒等式:arcsina+arccosa=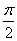 ;arctana+arccota=
;arctana+arccota=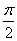 .
.
27.若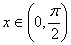 ,则sinx<x<tanx.
,则sinx<x<tanx.
28.三角与复数
(1)复数的4种形式: (
(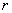 是复数的模)
是复数的模)
(2)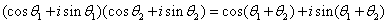
(3)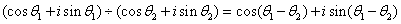
(4)隶莫弗公式:复数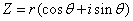 的
的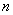 次方
次方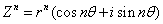
(5)复数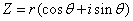 的
的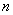 次方根为
次方根为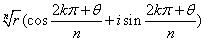
(6)方程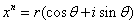 的解为
的解为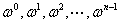 ,其中
,其中
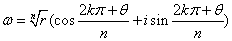
第二篇:初中函数基础知识总结
函数板块一:基础题
平面直角坐标系
1、如果p(a+b,ab)在第二象限,那么点Q (a,-b) 在第 象限.
2、已知点(1-a,a+2)在第二象限,则a的取值范围是
3、如果点M(a,b)第四象限,那么点N(b,a)在第 象限。
4、点A(-3,5)在第_____象限,到x轴的距离为______,到y轴的距离为_______。
5、平面直角坐标系中的P(3,-5),关于x轴对称的点 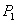 的坐标为 ;关于y轴对称的点
的坐标为 ;关于y轴对称的点 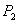 的坐标为 关于原点对称的点
的坐标为 关于原点对称的点 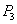 的坐标为 ;
的坐标为 ;
6、已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为 .
7、已知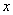 轴上点P到
轴上点P到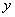 轴的距离是3,则点P坐标是_________。
轴的距离是3,则点P坐标是_________。
8、已知点M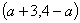 在
在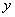 轴上,则点M的坐标为 。
轴上,则点M的坐标为 。
9、若点P到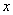 轴的距离为2,到
轴的距离为2,到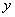 轴的距离为3,则点P的坐标为 _________
轴的距离为3,则点P的坐标为 _________
10、将点P(-3,2)向下平移3个单位,向左平移2个单位后得到点Q(x,y),则xy=___________
11、已知点M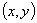 与点N
与点N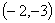 关于
关于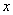 轴对称,则x + y = ____ 。
轴对称,则x + y = ____ 。
12、点Q(-4,5)到x轴的距离是 ,到y 轴的距离是
13、(-3,4)关于x轴对称的点的坐标为_________,关于y轴对称的点的坐标为__________,
关于原点对称的坐标为__________.
14、点B(-5,-2)到x轴的距离是____,到y轴的距离是____,到原点的距离是____
函数取值范围
1函数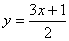 的自变量x的取值范围是 ( )
的自变量x的取值范围是 ( )
A.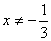 B.x≠一3 C.x取任意实数 D.
B.x≠一3 C.x取任意实数 D.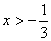
2、函数 的自变量x的取值范围是 ( )
的自变量x的取值范围是 ( )
A.x<2 B.x≤2 C. x≥2 D.x>2
3、函数y=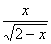 的自变量x的取值范围_________________
的自变量x的取值范围_________________
4、求下列函数的自变量取值范围:
①y=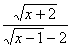 ; ②y=
; ②y=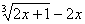
正比例函数和一次函数
1、已知一个正比例函数经过点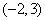 ,求它的解析式。
,求它的解析式。
2、(1)已知y与x+1成正比例,当x=5时,y=12,则y关于x的函数解析式是________.
(2)y与3x成正比例,当x=8时,y=-12,则y与x的函数解析式为___________
3、一个函数是经过原点的直线,并且这条直线经点(2,-3a)和点(1,a-5),求这个一次函数的解析式。
4、已知一个一次函数经过点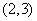 和点
和点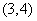 ,求它的解析式。
,求它的解析式。
5、已知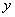 是
是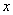 的一次函数,且当
的一次函数,且当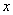 =8时,
=8时,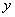 =15:当
=15:当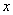 =-10时,
=-10时,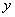 =-3,
=-3,
求:⑴这个一次函数的解析式;
⑵当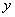 =-2时,求
=-2时,求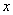 的值;
的值;
6、已知函数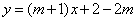
(1)若函数图象经过原点,求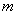 的值
的值
(2)若这个函数是一次函数,且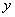 随着
随着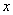 的增大而减小,求
的增大而减小,求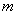 的取值范围.
的取值范围.
7、直线y=3-9x与x轴的交点坐标为__________,与y轴的交点坐标为________.
8、若直线y=kx+b平行直线y=3x+4,且过点(1,-2),则k=________ .
9、已知一次函数y =(m + 4)x + m + 2(m为整数)的图象不经过第二象限,则m =________
(2002年温州市中考试题)
10、旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购买行李票.设行李票y(元)是行李重量x(千克)的一次函数,如图6-20所示,求
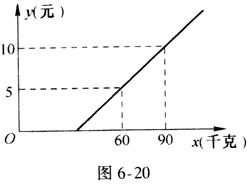
(1)y与x之间的函数关系式;
(2)旅客最多可免费携带行李的重量.
12、某商场计划投入一笔资金采购一批紧俏商品,经过市调查发现,如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费用700元,请问根据商场的资金状况如何购销获利较多?
(2001年山西省中考试题)
反比例函数
1、反比例函数y= 图象经过点(2,3),则n的值是( ).
图象经过点(2,3),则n的值是( ).
A、-2 B、-1 C、0 D、1
2、若反比例函数y=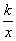 (k≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ).
(k≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ).
A、(2,-1) B、(-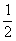 ,2) C、(-2,-1) D、(
,2) C、(-2,-1) D、(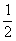 ,2)
,2)
3、已知y与(2x+1)成反比例且当x=0时,y=2,那么当x=-1时,y=________。
4、反比例函数y=(m+2)xm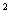 -10的图象分布在第二、四象限内,则m的值为
-10的图象分布在第二、四象限内,则m的值为
5、已知反比例函数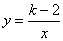 的图象位于第一、三象限,则
的图象位于第一、三象限,则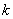 的取值范围
的取值范围
是 .
已知一次函数y=ax+b的图象经过第一、二、四象限,则函数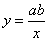 的图象在第________象限.
的图象在第________象限.
6、已知反比例函数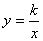 的图象分布在第二、四象限,则在一次函数
的图象分布在第二、四象限,则在一次函数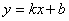 中,
中,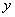 随
随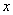 的增大而 (填“增大”或“减小”或“不变”).
的增大而 (填“增大”或“减小”或“不变”).
7、已知一次函数y=ax+b的图像与反比例函数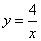 的图像交于A(2,2),B(-1,m),求一次函数的解析式;
的图像交于A(2,2),B(-1,m),求一次函数的解析式;
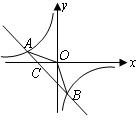 8、如图,已知
8、如图,已知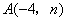 ,
,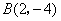 是一次函数
是一次函数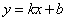 的图像和反比例函数
的图像和反比例函数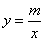 的图像的两个交点.
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线 与
与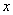 轴的交点
轴的交点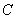 的坐标及三角形
的坐标及三角形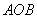 的面积.
的面积.
(3)当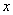 为何值时,一次函数的值小于反比例函数的值?
为何值时,一次函数的值小于反比例函数的值?
二次函数
1.函数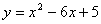 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A.全体实数 B.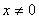 C
C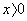
 D
D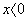
2、配方法求二次函数的最大(小)值,和对称轴
例:(1) (2)
(2)
(3)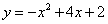
 (4)
(4)
3、用公式法求二次函数的最大(小)值,和对称轴
(1)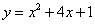 (2)
(2)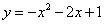
4、求二次函数的解析式
(1)已知二次函数的解析式为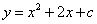 ,它的图像经过点
,它的图像经过点 ,求出它的解析式;
,求出它的解析式;
(2)已知二次函数的解析式为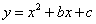 ,它的图像经过点
,它的图像经过点 和点
和点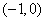 ,求出它的解析式;
,求出它的解析式;
(3)已知二次函数的解析式为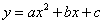 ,它的图像经过点
,它的图像经过点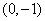 和点
和点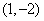 和点
和点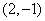 ,求出它的解析式;
,求出它的解析式;
(4)已知二次函数的顶点式为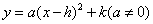 ,它的图像的最高点为
,它的图像的最高点为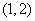 ,而且经过点
,而且经过点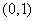 ,求它的解析式。
,求它的解析式。
5、已知二次函数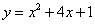 ,它与
,它与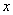 轴相交于点
轴相交于点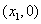 和点
和点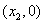
(1)求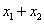 ,
,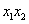 (2)求
(2)求 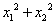 ,
,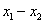
6、已知抛物线y= x2+x-
x2+x-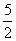 .
.
(1)用配方法求出它的顶点坐标和对称轴;
(2)若抛物线与x轴的两个交点为A、B,求线段AB的长.
7、y=(m-2)xm2- m 是关于x的二次函数,则m=( )
A -1 B 2 C -1或2 D m不存在
8、将一抛物线向下向右各平移2个单位得到的抛物线是y=-x2,则抛物线的解析式是( )
A y=—( x-2)2+2 B y=—( x+2)2+2
C y=— ( x+2)2+2 D y=—( x-2)2—2
9、抛物线y= 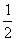 x2-6x+24的顶点坐标是( )
x2-6x+24的顶点坐标是( )
A (—6,—6) B (—6,6) C (6,6) D(6,—6)
函数y=ax2-bx+c(a≠0)的图象过点(-1,0),则
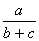 =
= =
= 的值是( )
的值是( )
A -1 B 1 C 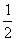 D -
D -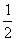

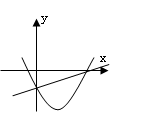
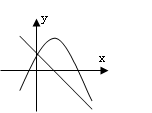
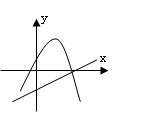
 10、已知一次函数y= ax+c与二次函数y=ax
2+bx+c(a≠0),它们在同一坐标系内的大致图象是图中的( )
10、已知一次函数y= ax+c与二次函数y=ax
2+bx+c(a≠0),它们在同一坐标系内的大致图象是图中的( )
A B C D
11、无论m为任何实数,总在抛物线y=x2+2mx+m上的点的坐标是———————————————。
第三篇:三角函数知识总结与综合检测
三角函数知识总结与综合检测
A级
一、选择题
1.在直角坐标系中,若角α与角β的终边关于x轴对称,则α与β的关系一定是( )
A.α=-β B.α+β=k·360°(k∈Z)
C.α-β=k·360°(k∈Z) D.以上答案都不对
2.圆内一条弦的长等于半径,这条弦所对的圆心角是( )
A.等于1弧度 B.大于1弧度
C.小于1弧度 D.无法判断
3.在△ABC中,如果sinA+cosA=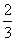 ,则△ABC是( )
,则△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
4.已知:sinα+cosα=-1,则tanα+cotα的值是( )
A.1 B.-1 C.0 D.不存在
5.y=cos|x|-cosx的值域是( )
A.[-1,1] B.0 C.[-2,0] D.[0,2]
6.下列各函数中,奇函数的个数是( )
(1)y=sinx (2)y=cosx
(3)y=tanx (4)y=secx
(5)y=lg(sinx+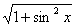 )
)
(6)y=lg(cosx+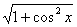 )
)
A.1 B.2 C.3 D.4
7.若y=sin(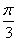 -α)=
-α)= 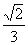 ,则y=sin(
,则y=sin(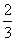 π+α)的值是( )
π+α)的值是( )
A. 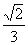 B.-
B.- 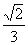 C.
C. 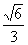 D.-
D.- 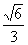
8.方程sinx=lgx的实根的个数是( )
A.1 B.2个 C.3个 D.3个以上
9.若sin(α+β)= 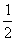 ,sin(α-β)=
,sin(α-β)= 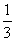 ,则
,则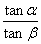 的值是( )
的值是( )
A. 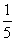 B.-
B.- 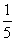 C.5 D.-5
C.5 D.-5
10.若x=cos36°-cos72°,则x的值为( )
A. 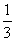 B.
B. 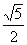 C.
C. 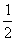 D.-
D.- 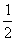
11.函数y=3sin(2x+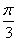 )的图像可以看成把函数y=3sin2x的图像经过下列平移而得到的( )
)的图像可以看成把函数y=3sin2x的图像经过下列平移而得到的( )
A.向左平移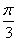 个单位 B.向右平移
个单位 B.向右平移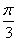 个单位
个单位
C.向左平移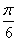 个单位 D.向右平移
个单位 D.向右平移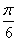 个单位
个单位
12.下列四命题中正确的应当是( )
①y=tanx恒为增函数;②y=cotx在x∈(-π,0)∪(0,π)上是周期函数;③y=cosx在(-π,π)上为偶函数;④y=sinx在x∈[-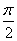 ,
,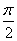 ]上为奇函数.
]上为奇函数.
A.① B.①② C.②③ D.④
二、填空题
1.如果函数y=sin2x+acos2x的图像关于直线x=-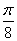 对称,那么a= .
对称,那么a= .
2.函数y=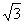 sin2x-3cos2x的单调递减区间为 .
sin2x-3cos2x的单调递减区间为 .
3.arctan1+arctan2+arctan3的值是 .
4.若函数y=2cosx(0≤x≤2π)的图像和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积为 .
三、解答题
1.设α+β=150°,求sin2α+sin2β-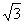 sinαsinβ的值.
sinαsinβ的值.
2.设x∈(-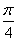 ,
,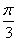 ),f(x)=
),f(x)=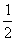 sin(x-
sin(x-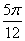 )cos(
)cos(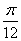 -x)+
-x)+ 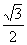 sin2(x-
sin2(x-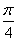 ),求f(x)的最大值和最小值.
),求f(x)的最大值和最小值.
3.已知sinα和cosα是方程x2-kx+k+1=0的两根,且0<α<2π,求k与α的值.
4.设关于sinx的方程sin2x-(a2+2a)sinx+a3+a2=0有实数解,求实数a的范围.
5.设0<α<π,0<β<π,且cosα+cosβ-cos(α+β)=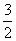 ,求α,β的值.
,求α,β的值.
6.求函数y=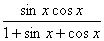 的值域.
的值域.
AA级
一、选择题
1.角的集合M={x|x=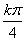 ,k∈Z},N={x|x=
,k∈Z},N={x|x=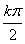 ±
±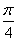 ,k∈Z},则M与N的关系是( )
,k∈Z},则M与N的关系是( )
A.M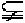 N B.M
N B.M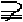 N C.M=N D.不能确定
N C.M=N D.不能确定
2.若集合A=R,B=R,则下列对应f:x→y是A到B的映射的是( )
A.y=tanx B.y=cotx C.y=secx D.y=cosx
3.若θ是第三象限的角,且cos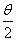 <0,那么
<0,那么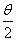 是( )
是( )
A.第一象限的角 B.第二象限的角
C.第三象限的角 D.第四象限的角
4.函数y=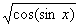 的定义域为( )
的定义域为( )
A.[2kπ-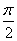 ,2kπ+
,2kπ+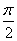 ](k∈Z) B.[2kπ,2kπ+
](k∈Z) B.[2kπ,2kπ+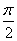 ](k∈Z)
](k∈Z)
C.[2kπ,2kπ+π](k∈Z) D.R
5.在△ABC中,若sin(A+B-C)=sin(A-B+C),则△ABC必是( )
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.等腰直角三角形
6.函数y=lgsinx+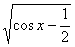 的定义域是( )
的定义域是( )
A.2kπ<x≤2kπ+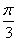 (k∈Z) B.2kπ≤x≤2kπ+
(k∈Z) B.2kπ≤x≤2kπ+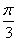 (k∈Z)
(k∈Z)
C.2kπ<x≤2kπ+π(k∈Z) D.2kπ<x≤2kπ+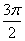 (k∈Z)
(k∈Z)
7.把函数y=sin2x的图像在y轴方向压缩一半,沿y轴正方向平移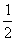 个单位,再沿x轴正方向平移
个单位,再沿x轴正方向平移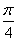 个单位,所得图像的函数表达式是( )
个单位,所得图像的函数表达式是( )
A.y=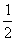 +
+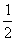 sin2(x-
sin2(x-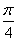 ) B.y=
) B.y=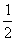 sin(2x-
sin(2x-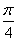 )-
)-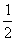
C.y=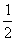 sin2(x-
sin2(x-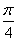 ) D.y=
) D.y=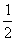 sin2(x+
sin2(x+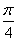 )
)
8.已知函数:①f(x)=sinx2;②f(x)=sin2x;③f(x)=tan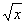 ;④f(x)=
;④f(x)= 其中周期函数是( )
其中周期函数是( )
A.①和③ B.①和④ C.②和③ D.②和④
9.设α、β为锐角,则sin(α+β)与sinα+sinβ的值满足关系式( )
A.sin(α+β)>sinα+sinβ B.sin(α+β)<sinα+sinβ
C.sin(α+β)=sinα+sinβ D.以上结论都不对
10.已知cosα=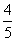 ,cos(α+β)=
,cos(α+β)= 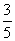 ,且α、β为锐有,那么sinβ的值是( )
,且α、β为锐有,那么sinβ的值是( )
A. 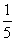 B.
B. 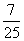 C.
C. 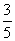 D.
D. 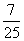
11.方程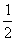 cos(
cos(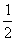 x+
x+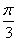 )=1的解集是( )
)=1的解集是( )
A.{x|x=4kπ,k∈Z} B.{x|x=4kπ±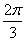 -
-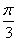 ,k∈Z}
,k∈Z}
C.{x|x=kπ±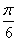 -
-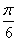 ,k∈Z} D.
,k∈Z} D.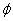
12.在区间(0,π)上满足cos5x=cos2x的值的个数是( )
A.3 B.4 C.5 D.6
二、填空题
1.函数y=arctan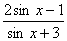 的值域是为 .
的值域是为 .
2.两弧度的圆心角所对的弦长为2,这个圆心角所夹的扇形的面积为 .
3.函数y=2|sin(4x-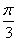 )|的最小正周期是 .
)|的最小正周期是 .
4.若sinx+cosx=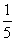 ,x∈[0,π],那么tanx= .
,x∈[0,π],那么tanx= .
三、解答题
1.设6sin3β-cos22α=6,求α、β.
2.已知关于x的方程
(2cosθ-1)x2-4x+4cosθ+2=0有两个不相等的正根,且θ为锐角,求θ的范围.
3.设cos(α-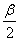 )=-
)=-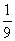 ,sin(
,sin(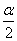 -β)=
-β)= 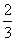 ,且
,且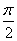 <α<π,0<β<
<α<π,0<β<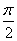 ,求cos(α+β)的值.
,求cos(α+β)的值.
4.求函数y=sin2x+9cos2x-8sinxcosx的最值及其相对应的x的值.
5.已知AB=2a,在以AB为直径的半圆上有一点C,设AB中点为O,∠AOC=60°.
(1)在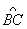 上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;
上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;
(2)设f(θ)=PA+PB+PC,当θ为何值时f(θ)有最大值,最大值是多少?
6.已知sinα+sinβ=m,cosα+cosβ=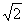 .
.
(1)求实数m的范围.
(2)当m取最小值时,求sin(α+β)的值.
参考答案:
A级
一、1.B 2.B 3.C 4.D 5.B 6.C 7.A 8.C 9.C 10.C 11.C 12.D
二、1.-1 2.[kπ+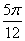 ,kπ+
,kπ+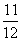 π](k∈Z) 3.π 4.4π
π](k∈Z) 3.π 4.4π
三、1. 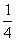 2.x=
2.x=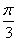 时,最大值为
时,最大值为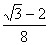 ,x=
,x=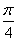 时,最小值为-
时,最小值为-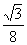 3.k=-1,α=π或
3.k=-1,α=π或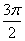 或
或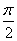 4.
4. 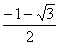 ≤a≤1 5.α=β=
≤a≤1 5.α=β=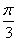 6.[-
6.[-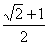 ,-1]∪(-1,
,-1]∪(-1, 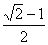 )
)
AA级
一、1.B 2.D 3.B 4.D 5.C 6.A 7.A 8.D 9.B 10.B 11.D 12.C
二、1.[arccot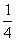 ,π-arccot
,π-arccot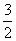 ]
]
2. 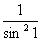 3.
3.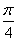 4.-
4.- 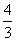
三、1.α=kπ±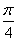 ,β=
,β= +
+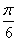 ,(k,n∈Z)
,(k,n∈Z)
2.30°<θ<60° 3.- 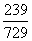 4.x=kπ-
4.x=kπ-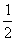 arctan
arctan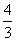 ,(k∈Z)时,ymax=11
,(k∈Z)时,ymax=11
x=kπ+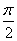 -
-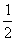 arctan
arctan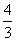 (k∈Z)时ymin=1
(k∈Z)时ymin=1
5.(1)f(θ)=2acosθ+2asinθ+2asin(60°-θ)
(2)当θ=15°时,f(θ)max=(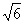 +
+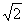 )a
)a
6.(1)m∈[-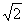 ,
,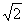 ] (2)m=-
] (2)m=-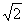 时,sin(α+β)=-1
时,sin(α+β)=-1
-
三角函数知识总结与综合检测
三角函数知识总结与综合检测A级一、选择题1.在直角坐标系中,若角α与角β的终边关于x轴对称,则α与β的关系一定是()A.α=-βC…
-
必修4 三角函数知识点归纳总结
必修4三角函数知识网络应用一任意角的概念与弧度制1将沿x轴正向的射线围绕原点旋转所形成的图形称作角逆时针旋转为正角顺时针旋转为负角…
-
三角函数知识点总结
黄黄帝帝内内经经文文言言文文全全篇篇高中数学第四章三角函数考试内容角的概念的推广弧度制任意角的三角函数单位圆中的三角函数线同角三角…
-
高考数学之三角函数知识点总结
三角函数一基础知识定义1角一条射线绕着它的端点旋转得到的图形叫做角若旋转方向为逆时针方向则角为正角若旋转方向为顺时针方向则角为负角…
-
高中数学三角函数知识点总结(原创版)1
高(文一四六专用)1.特殊角的三角函数值:2.角度制与弧度制的互化:3600?2?,1800??,1rad=180°≈57.30°…
-
高一三角函数知识点的梳理总结
1.2.高一三角函数知识一1.1任意角和弧度制?正角:逆时针方向旋转?1..任意角?负角:顺时针防线旋转?零角?2.象限角:在直角…
-
《三角函数及解直角三角形》知识点总结
Ⅰ、本章知识结构框图:Ⅱ、本章知识点:1、正弦、余弦、正切、余切的概念在是三角形ABC中,∠C=90°,(1)锐角A的对边与斜边的…
-
高一三角函数知识点的梳理总结
1.2.高一三角函数知识一1.1任意角和弧度制?正角:逆时针方向旋转?1..任意角?负角:顺时针防线旋转?零角?2.象限角:在直角…
-
高中数学三角函数知识点总结
高中数学之三角函数1.①与?(0°≤?<360°)终边相同的角的集合(角?与角?的终边重合):??|??k?360??,k?Z??…
-
锐角三角函数知识点总结与习题训练(
1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。2、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(…
-
个税知识总结
个人所得税【发布日期】:20xx年x月x日字体:【大】【中】【小】(一)纳税人个人所得税以所得人为纳税人,具体分为下列2种情况:1…