第二篇：高中数学概念公式总结

高中数学概念总结

高中数学概念公式总结

一、 函数

1、 若集合A中有n(n?N)个元素，则集合A的所有不同的子集个数为

2n，所有非空真子集的个数是2n?2。

二次函数y?ax2?bx?c的图象的对称轴方程是x??b，顶点坐2a

?b4ac?b2?标是???2a4a??。用待定系数法求二次函数的解析式时，解??

析式的设法有三种形式，即f(x)?ax2?bx?c（一般式），

和f(x)?a(x?x1)?(x?x2（零点式）)

（顶点式）。

2、 幂函数y?x ，当n为正奇数，m为正偶数，m<n时，其大致图象

是

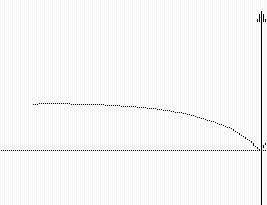
mnf(x)?a(x?m)2?n

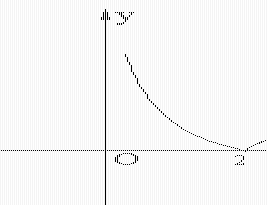
23、 函数y?x?5x?6的大致图象是

高中数学概念总结

??)，单调递增区间是由图象知，函数的值域是[0，

[2，2.5]和[3，??)，单调递减区间是(??，2]和[2.5，3]。

二、 三角函数

1、 以角?的顶点为坐标原点，始边为x轴正半轴建立直角坐标系，在角

?的终边上任取一个异于原点的点P(x,y)，点P到原点的距离记为

则sin?=r，yxyrxr，cos?=，tg?=，ctg?=，sec?=，csc?=。 rxrxyy222、同角三角函数的关系中，平方关系是：sin??cos??1，

1?tg2??sec2?，1?ctg2??csc2?；

倒数关系是：tg??ctg??1，sin??csc??1，cos??sec??1； 相除关系是：tg??sin?cos?，ctg??。 cos?sin?

3、诱导公式可用十个字概括为：sin(3?15???)??cos?，ctg(??)=tg?，tg(3???)??tg?。 22

?x(??)?B（其中A?0，??0）的最大值是4、 函数y?Asin

高中数学概念总结

A?B，最小值是B?A，周期是T?2?

?，频率是f??，相位2?

是?x??，初相是?；其图象的对称轴是直线?x???k???

2(k?Z)，凡是该图象与直线y?B的交点都是该

图象的对称中心。

5、 三角函数的单调区间：

x的递增区间是?2k?? y?sin?

??2，2k????(k?Z)，递减区间是?2?

?3???(k?Z)；y?cosx的递增区间是2k??，2k????22??

递减区间是?2k?，?2k???，2k??(k?Z)，2k????(k?Z)，y?tgx的

递增区间是?k???

??2，k?????(k?Z)，y?ctgx的递减区间是2?

?k?，k????(k?Z)。

6、sin(???)?sin?cos??cos?sin?

?(??)?co?scos??sin?sin? cos

tg(???)?tg??tg? 1?tg??tg?

7、二倍角公式是：sin2?=2sin??cos?

cos2?=cos??sin?=2cos??1=1?2sin? 2222

高中数学概念总结

tg2?=

2tg?

。

1?tg2?

3

3

8、三倍角公式是：sin3?=3sin??4sin? cos3?=4cos??3cos? 9、半角公式是：sin

??1?cos??cos?

=? cos=? 2222

tg

?sin?1?cos?1?cos?=?==。

sin?1?cos?21?cos?

2

10、升幂公式是：1?cos??2cos11、降幂公式是：sin??

2

?

2

1?cos??2sin

2

?

2

。

1?cos2?1?cos2?2

cos??。 22

2tg

12、万能公式：sin?=

?

21?tg2

cos?=

?

tg?=2

2tg1?tg

?

21?tg

2

1?tg

2

2

13、sin(???)sin(???)=sin2??sin2

cos(???)cos(???)=cos2??sin2

?，

?=cos2??sin2?。

14、4sin?sin(60??)sin(60??)=sin3?； 4cos?cos(60??)cos(60??)=cos3?； tg?tg(60??)tg(60??)=tg3?。 15、ctg??tg?=2ctg2?。

16、sin180=

?1

。 4

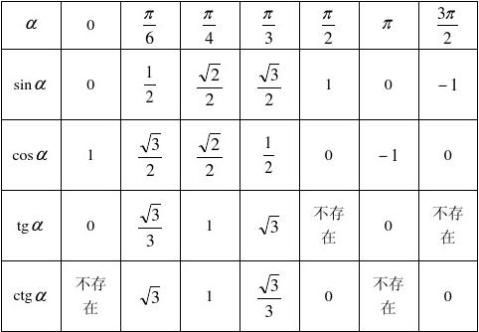
17、特殊角的三角函数值：

高中数学概念总结

18、正弦定理是（其中R表示三角形的外接圆半径）：

abc

???2R sinAsinBsinC

19、由余弦定理第一形式，b=a?c?2accosB

2

2

2

a2?c2?b2

由余弦定理第二形式，cosB=

2ac

20、△ABC的面积用S表示，外接圆半径用R表示，内切圆半径用r表

示，半周长用p表示则：

11

a?ha??；②S?bcsinA??； 22

abc2

③S?2RsinAsinBsinC；④S?；

4R

①S?⑤S?

p(p?a)(p?b)(p?c)；⑥S?pr

21、三角学中的射影定理：在△ABC 中，b?a?cosC?c?cosA，… 22、在△ABC 中，A?B?sinA?sinB，… 23、在△ABC 中：

sin(A+B)=sinCcos(A+B) ?-cosCtg(A+B) ?-tgC

高中数学概念总结

siA?BCA?BCA?BC?co co?si tg?ct 222222

?tgB?tgC?tgA?tgB?tgC tgA

24、积化和差公式： 1[sin(???)?sin(???)]， 2

1②cos??sin??[sin(???)?sin(???)]， 2

1③cos??cos??[cos(???)?cos(???)]， 2

1④sin??sin???[cos(???)?cos(???)]。 2①sin??cos??

25、和差化积公式： x?yx?y?cos， 22

x?yx?y?sin②sinx?siny?2cos， 22

x?yx?y?cos③cosx?cosy?2cos， 22

x?yx?y?sin④cosx?cosy??2sin。 22①sinx?siny?2sin

三、 反三角函数

1、y?arcsinx的定义域是[-1，1]，值域是[???]，奇函数，增函数； 22

s的定义域是[-1，1]，值域是[0，?]，非奇非偶，减函数； y?arccox

x y?arctg的定义域是R，值域是(???)，奇函数，增函数； 22

x y?arcctg的定义域是R，值域是(0，?)，非奇非偶，减函数。

，1]时，sin(arcsinx)?x，cos(arccosx)?x； 2、当x?[?1

sin(arccosx)??x2，cos(arcsinx)??x2

高中数学概念总结

arcsin(?x)??arcsinx，arccos(?x)???arccosx

arcsinx?arccosx?

对任意的x?R，有： ?2

tg(arctgx)?x，ctg(arcctgx)?x

arctg(?x)??arctgx，arcctg(?x)???arcctgx arctgx?arcctgx??

2

11，ctg(arctgx)?。 xx当x?0时，有：tg(arcctgx)?

3、最简三角方程的解集：

a?1时，sinx?a的解集为?；

a?1时，sinx?a的解集为xx?n??(?1)n?arcsina，n?Za?1时，cosx?a的解集为?；?? ?xx?2n??arccosa，n?Z?；a?1时，cosx?a的解集为

?xx?n??arctga，n?Z?；a?R，方程tgx?a的解集为

?xx?n??arcctga，n?Z?。a?R，方程ctgx?a的解集为

四、 不等式

nn1、若n为正奇数，由a?b可推出a?b吗？ （ 能 ）

若n为正偶数呢？ （仅当a、b均为非负数时才能）

2、同向不等式能相减，相除吗 （不能）

能相加吗？ （ 能 ）

能相乘吗？ （能，但有条件）

a?b?ab 2

a?b?c?abc 三个正数的均值不等式是：33、两个正数的均值不等式是：

n个正数的均值不等式是：a1?a2???an?a1a2?an n

高中数学概念总结

4、两个正数a、b的调和平均数、几何平均数、算术平均数、均方根之间的关系是

a?b?ab??112?ab2a2?b2 2

6、 双向不等式是：a?b?a?b?a?b

左边在ab?0(?0)时取得等号，右边在ab?0(?0)时取得等号。

五、 数列

1、等差数列的通项公式是an?a1?(n?1)d，前n项和公式是：Sn?n(a1?an)1 =na1?n(n?1)d。 22

2、等比数列的通项公式是an?a1qn?1，

?na1(q?1)?n前n项和公式是：Sn??a1(1?q) (q?1)??1?q

3、当等比数列?an?的公比q满足q<1时，limSn=S=n??a1。一般地，1?q

如果无穷数列?an?的前n项和的极限limSn存在，就把这个极限称为这n??

个数列的各项和（或所有项的和），用S表示，即S=limSn。 n??

4、若m、n、p、q∈N，且m?n?p?q，那么：当数列?an?是等差数列时，有am?an?ap?aq；当数列?an?是等比数列时，有am?an?ap?aq。

高中数学概念总结

5、 等差数列?an?中，若Sn=10，S2n=30，则S3n

6、等比数列?an?中，若Sn=10，S2n=30，则S3n；

六、 复数

1、 i怎样计算？（先求n被4除所得的余数，i

2、 ?1??n4k?r?ir） 11?i、?2???i是1的两个虚立方根，并且： 2222

1??2 1??1 32?13??2?1 ?12??2 ?2??1 ?1?2

1??2 2??1 ?1??2??1

3、 复数集内的三角形不等式是：z1?z2?z1?z2?z1?z2，其中复数z、z对应的向量共线且同向（反向）时取等号。

4、 棣莫佛定理是：?r(cos??isin?)??rn(cosn??isinn?)(n?Z) n

5、 若非零复数z?r(cos??isin?)，则z的n次方根有个，即：

zk?r(cos2k???2k????isin)(k?0，1，2，?，n?1) nn

它们在复平面内对应的点在分布上有什么特殊关系？ 都位于圆心在原点，半径为r的圆上，并且把这个圆n等分。

6、 若z1?2，z2?3(cos??isin)?z1，复数z1、z2对应的点分别是33

1??2?6?sin?33。 23?A、B，则△AOB（O为坐标原点）的面积是

27、 z?z=z。

8、 复平面内复数z对应的点的几个基本轨迹：

高中数学概念总结

①argz??(?为实常数)?轨迹为一条射线。 ②arg(z?z0)??(z0是复常数， ?是实常数）?轨迹为一条射线。 ③z?z0?r(r是正的常数）?轨迹是一个圆。 ④z?z1?z?z2(z1、z2是复常数)?轨迹是一条直线。 ⑤z?z1?z?z2?2a(z1、z2是复常数，a是正的常数）?轨迹有三种可能情形：a)当2a?z1?z2时，轨迹为椭圆；b)当

2a?z1?z2时，轨迹为一条线段；c)当2a?z1?z2时，轨迹不存在。

⑥z?z1?z?z2?2a(a是正的常数)?轨迹有三种可能情形：a)当2a?z1?z2时，轨迹为双曲线；b) 当2a?z1?z2时，轨迹为两条射线；c) 当2a?z1?z2时，轨迹不存在。

七、 排列组合、二项式定理

1、 加法原理、乘法原理各适用于什么情形？有什么特点？ 加法分类，类类独立；乘法分步，步步相关。

2、排列数公式是：Pnm=n(n?1)?(n?m?1)=

m 排列数与组合数的关系是：Pnm?m！ ?Cnn！； (n?m)！

m 组合数公式是：Cn=n(n?1)?(n?m?1)n！=； 1?2???mm！?(n?m)！

mn?mm?1m 组合数性质：Cn=Cn Cn+Cn=Cn?1

nm?C

r?0rn=2 rCn=nCn?1 nrr?1

高中数学概念总结

rr?1Crr?Crr?1?Crr?2???Cn?Cn?1

3、 二项式定理：

0n1n?12n?22rn?rrnn(a?b)n?Cna?Cnab?Cnab???Cnab???Cnb

rn?rr1，2?，n) 二项展开式的通项公式：Tr?1?Cnab(r?0，

八、 解析几何

1、 沙尔公式：AB?xB?xA

2、 数轴上两点间距离公式：?xB?xA

3、 直角坐标平面内的两点间距离公式：

P1P2?(x1?x2)2?(y1?y2)2

4、 若点P分有向线段P1P2成定比λ，则λ=P1P PP2

5、 若点P1(x1,y1)，P2(x2,y2)，P(x,y)，点P分有向线段P1P2成定比

λ，则：λ=x?x1y?y1=； x2?xy2?y

x1??x2 1??

y1??y2 1?? x= y=

若A(x1,y1)，B(x2,y2)，C(x3,y3)，则△ABC的重心G的坐标是?x1?x2?x3y1?y2?y3???。 33??

高中数学概念总结

6、求直线斜率的定义式为k=tg?，两点式为k=

7、直线方程的几种形式： y2?y1。 x2?x1

点斜式：y?y0?k(x?x0)， 斜截式：y?kx?b 两点式：y?y1x?x1xy， 截距式：??1 ?aby2?y1x2?x1

一般式：Ax?By?C?0

经过两条直线l1：A1x?B1y?C1?0和l2：A2x?B2y?C2?0的

交点的直线系方程是：A1x?B1y?C1??(A2x?B2y?C2)?0

8、 直线l1：y?k1x?b1，l2：y?k2x?b2，则从直线l1到直线l2的角

θ满足：tg??k2?k1 1?k1k2

k2?k1 1?k1k2直线l1与l2的夹角θ满足：tg??

直线l1：A1x?B1y?C1?0，l2：A2x?B2y?C2?0，则从直线l1到直线l2的角θ满足：tg??A1B2?A2B1 A1A2?B1B2

A1B2?A2B1 A1A2?B1B2直线l1与l2的夹角θ满足：tg??

9、 点P(x0,y0)到直线l：Ax?By?C?0的距离：

d?Ax0?By0?C

A?B22

高中数学概念总结

10、两条平行直线l1：Ax?By?C1?0，l2：Ax?By?C2?0距离是

d?C1?C2

A?B22

11、圆的标准方程是：(x?a)2?(y?b)2?r2

圆的一般方程是：x2?y2?Dx?Ey?F?0(D2?E2?4F?0) 其中，半径是r?D2?E2?4FE??D，圆心坐标是??，?? 2?2?2

22思考：方程x2?y2?Dx?Ey?F?0在D?E?4F?0和

D2?E2?4F?0时各表示怎样的图形？

12、若A(x1,y1)，B(x2,y2)，则以线段AB为直径的圆的方程是

(x?x1)(x?x2)?(y?y1)(y?y2)?0

经过两个圆

x2?y2?D1x?E1y?F1?0，x2?y2?D2x?E2y?F2?0 的交点的圆系方程是：

x2?y2?D1x?E1y?F1??(x2?y2?D2x?E2y?F2)?0

22 经过直线l：Ax?By?C?0与圆x?y?Dx?Ey?F?0的

交点的圆系方程是：x?y?Dx?Ey?F??(Ax?By?C)?0

13、圆x?y?r的以P(x0,y0)为切点的切线方程是 22222

x0x?y0y?r2

一般地，曲线Ax?Cy?Dx?Ey?F?0的以点P(x0，y0)为切点22

高中数学概念总结

的切线方程是：Ax0x?Cy0y?D?x?x0y?y0?E??F?0。例如，抛22

x?1，即：2，2)为切点的切线方程是：2y?4?物线y2?4x的以点P(1

y?x?1。

注意：这个结论只能用来做选择题或者填空题，若是做解答题，只能按照求切线方程的常规过程去做。

14、研究圆与直线的位置关系最常用的方法有两种，即：

①判别式法：Δ>0，=0，<0，等价于直线与圆相交、相切、相离； 半径、小于半径，等价于直线与圆相离、相切、相交。

15、抛物线标准方程的四种形式是：y2?2px，y2??2px，

x2?2py，x2??2py。

16、抛物线y?2px的焦点坐标是：?

22p?p? ，0?，准线方程是：x??。2?2? 若点P(x0,y0)是抛物线y?2px上一点，则该点到抛物线的焦点的距离（称为焦半径）是：x0?p，过该抛物线的焦点且垂直于抛2

物线对称轴的弦（称为通径）的长是：2p。

x2y2y2x2

17、椭圆标准方程的两种形式是：2?2?1和2?2?1 abab

(a?b?0)。

x2y2

0)，准线方程是18、椭圆2?2?1(a?b?0)的焦点坐标是(?c，ab

高中数学概念总结

ca22b2222

x??，离心率是e?，通径的长是。其中c?a?b。

aca

x2y2

19、若点P(x0,y0)是椭圆2?2?1(a?b?0)上一点，F1、F2是

ab

其左、右焦点，则点P的焦半径的长是PF1?a?ex0和

PF2?a?ex0。

x2y2y2x2

20、双曲线标准方程的两种形式是：2?2?1和2?2?1

abab(a?0，b?0)。

x2y2a2

0)，准线方程是x??21、双曲线2?2?1的焦点坐标是(?c，，

cab

c2b2x2y2

离心率是e?，通径的长是，渐近线方程是2?2?0。

aaab

其中c?a?b。

2

2

2

x2y2

22、与双曲线2?2?1共渐近线的双曲线系方程是

ab

x2y2x2y2

???(??0)。与双曲线2?2?1共焦点的双曲线系方a2b2abx2y2

?2?1。 程是2

a?kb?k

23、若直线y?kx?b与圆锥曲线交于两点A(x1，y1)，B(x2，y2)，则弦

长为 AB?

(1?k2)(x1?x2)2；

若直线x?my?t与圆锥曲线交于两点A(x1，y1)，B(x2，y2)，则弦

高中数学概念总结

长为 AB?(1?m2)(y1?y2)2。

24、圆锥曲线的焦参数pb2双曲线都有：p?。 c

25、平移坐标轴，使新坐标系的原点O?在原坐标系下的坐标是（h，k），

若点P在原坐标系下的坐标是(x,y)，在新坐标系下的坐标是(x?,y?)，则x?=x?h，y?=y?k。

九、 极坐标、参数方程

1、 经过点P0(x0,y0)的直线参数方程的一般形式是：

?x?x0?at(t是参数)。 ??y?y0?bt

2、 若直线l经过点P0(x0,y0)，倾斜角为?，则直线参数方程的标准形

式是：??x?x0?tcos?

?y?y0?tsin?(t是参数)。其中点P对应的参数t的几何意义是：有向线段P0P的数量。

若点P1、P2、P是直线l上的点，它们在上述参数方程中对应的参数分别是t1、t2和t，则：P1P2?t1?t2；当点P分有向线段P?时，t?1P2成定比

t?t1?t2。 2t1??t2；当点P是线段P1P2的中点时，1??

3、圆心在点C(a，b)，半径为r的圆的参数方程是：

高中数学概念总结

?x?a?rcos?(?是参数)。 ??y?b?rsin?

3、 若以直角坐标系的原点为极点，x轴正半轴为极轴建立极坐标系，点

s，P的极坐标为(?,?)，直角坐标为(x,y)，则x??co?

y??sin?，??x2?y2，tg??y。 x

4、 经过极点，倾斜角为?的直线的极坐标方程是：???或?????，

0)，且垂直于极轴的直线的极坐标方程是：?cos??a，经过点(a， 经过点(a)且平行于极轴的直线的极坐标方程是：?sin??a， ?

2

经过点(?0，?0)且倾斜角为?的直线的极坐标方程是：?sin?(??)??0sin?(0??)。

5、 圆心在极点，半径为r的圆的极坐标方程是??r；

圆心在点(a，0)，半径为a的圆的极坐标方程是??2acos?； 圆心在点(a)，半径为a的圆的极坐标方程是??2asin?； ?

2

圆心在点(?0，?0)，半径为r的圆的极坐标方程是

2?2??0?2??0cos(???0)?r2。

6、 若点M(?1，?1)、N(?2，?2)，则

2?2?1?2cos(?1??2)。 MN??12??2

十、 立体几何

1、求二面角的射影公式是cos??S?，其中各个符号的含义是：S是二S

高中数学概念总结

面角的一个面内图形F的面积，S?是图形F在二面角的另一个面内的射影，?是二面角的大小。

2、若直线l在平面?内的射影是直线l?，直线m是平面?内经过l的斜足的一条直线，l与l?所成的角为?1，l?与m所成的角为?2, l与m所成的角为θ，则这三个角之间的关系是cos??cos?1?cos?2。

3、体积公式：

柱体：V?S?h，圆柱体：V??r2?h。

斜棱柱体积：V?S??l（其中，S?是直截面面积，l是侧棱长）； 锥体：V?11S?h，圆锥体：V??r2?h。 33

1?h(S?S?S??S?)， 3

1?h(R2?R?r?r2) 3 台体：V?圆台体：V? 球体：V?

4、 侧面积： 4?r3。 3

直棱柱侧面积：S?c?h，斜棱柱侧面积：S?c??l； 正棱锥侧面积：S?11c?h?，正棱台侧面积：S?(c?c?)h?； 221c?l??rl， 2圆柱侧面积：S?c?h?2?rh，圆锥侧面积：S?

圆台侧面积：S?5、几个基本公式： 1(c?c?)l??(R?r)l，球的表面积：S?4?r2。 2

高中数学概念总结

弧长公式：l???r（?是圆心角的弧度数，?>0）；

扇形面积公式：S?1l?r； 2r?2?； lR?r?2?。 l 圆锥侧面展开图（扇形）的圆心角公式：?? 圆台侧面展开图（扇环）的圆心角公式：??

经过圆锥顶点的最大截面的面积为（圆锥的母线长为l，轴截面顶角

是θ）：

??12?lsin?(0???)?22 S??1???l2(????)2?2

十一、比例的几个性质

ac??ad?bc bd

acbd2、反比定理：??? bdac

acab3、更比定理：??? bdcd

aca?bc?d?5、 合比定理；?? bdbd

aca?bc?d?6、 分比定理：?? bdbd

aca?bc?d?7、 合分比定理：?? bda?bc?d

aca?bc?d?8、 分合比定理：?? bda?bc?d1、比例基本性质：

9、 等比定理：若aa1a2a3?????n，b1?b2?b3???bn?0，b1b2b3bn

高中数学概念总结

则a1?a2?a3???ana1?。 b1?b2?b3???bnb1

十二、复合二次根式的化简

A?B?A?A2?B?2

2A?A2?B 2当A?0，B?0，A?B是一个完全平方数时，对形如

式使用上述公式化简比较方便。 A?B的根