高中数学--不等式知识点归纳和分类习题测试
必修五:不等式
知识点一:不等式关系与不等式
【习题训练】
1. 下列命题中正确命题的个数是( )
①若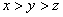 ,则
,则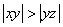 ;②
;②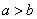 ,
,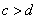 ,
, ,则
,则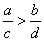 ;
;
③若 ,则
,则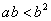 ;④若
;④若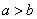 ,则
,则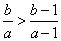 .
.
A.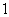 B.
B.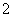 C.
C.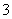 D.
D.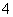
2.用“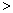 ”“
”“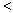 ”号填空:如果
”号填空:如果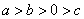 ,那么
,那么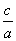 ________
________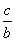 .
.
3.已知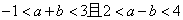 ,则2a+3b的取值范围是( )
,则2a+3b的取值范围是( )
A 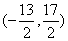 B
B 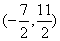 C
C 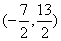 D
D 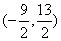
二、含有绝对值的不等式
1.绝对值的几何意义: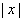 是指数轴上点
是指数轴上点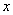 到原点的距离;
到原点的距离;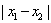 是指数轴上
是指数轴上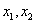 两点间的距离
两点间的距离
2、解含有绝对值不等式的主要方法:
(1)公式法: ,
, 或
或 .
.
(2)定义法:零点分段法; (3)平方法:不等式两边都是非负时,两边同时平方.
【典型例题】
1.不等式 的解集为( )(运用公式法)
的解集为( )(运用公式法)
A.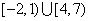 B.
B.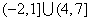 C.
C.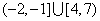 D.
D.
2. 求解不等式: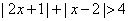 .(运用零点分段发)
.(运用零点分段发)
3.函数 的最小值为( ) (零点分段法)
的最小值为( ) (零点分段法)
A.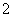 B.
B.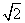 C.
C.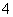 D.
D.
【习题训练】
1.解不等式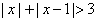
2.若不等式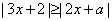 对
对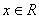 恒成立,则实数
恒成立,则实数 的取值范围为______。
的取值范围为______。
例1 .不等式 的解集是____________.
的解集是____________.
例2. 解不等式 例3. 解关于x的不等式
例3. 解关于x的不等式
例4. 不等式 ≥
≥ 的解集是( )
的解集是( )


 ≤
≤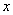 ≤
≤

 ≤
≤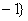

 ≤
≤

 ≤
≤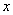 ≤
≤
三、不等式证明的几种常用方法
比较法(做差法、做商法)、综合法、分析法、换元法、反证法、放缩法。
【典型例题】
1.若 或
或 ,
, ,
,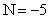 ,则
,则 与
与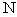 的大小关系是( )
的大小关系是( )
A. B.
B. C.
C. D.
D.
2.若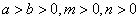 ,则
,则 ,
,  ,
, 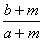 ,
,  按由小到大的顺序排列为
按由小到大的顺序排列为
3.若a=,b=,c=则a,b,c按从小到大排列应是________.
4.设a=2-,b=-2,c=5-2,则a、b、c之间的大小关系为________.
5.下列各式中,对任何实数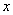 都成立的一个式子是( )
都成立的一个式子是( )
A.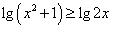 B.
B. C.
C. D.
D.
6. 若 、
、 是任意实数,且
是任意实数,且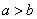 ,则( )
,则( )
A.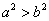 B.
B. C.
C. D.
D.
四、数轴穿跟法: 奇穿,偶不穿
例题:不等式 的解为( )
的解为( )
A.-1<x≤1或x≥2 B.x<-3或1≤x≤2
C.x=4或-3<x≤1或x≥2 D.x=4或x<-3或1≤x≤2
知识点二:一元二次不等式及其解法
二、一元二次不等式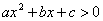 和
和 及其解法
及其解法
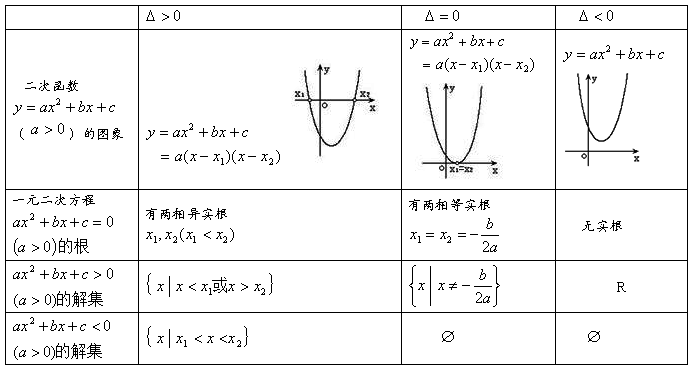
顺口溜:在二次项系数为正的前提下:大于型取两边,小于型取中间
分式不等式
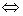 ,分式不等式
,分式不等式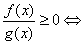 .
.
【典型例题】
1.设二次不等式 的解集为
的解集为 ,则ab的值为( )
,则ab的值为( )
A.-6 B.-5 C.6 D.5
2.已知函数 ,若x的取值范围是全体实数,则实数a的取值范围是( )
,若x的取值范围是全体实数,则实数a的取值范围是( )
A. B.
B.  C.
C.  D.
D. 
3.若不等式 的解集为
的解集为 ,则( )
,则( )
A. 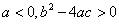 B.
B. 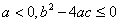 C.
C.  D.
D. 
4.若关于实数x的方程 有一正根和一负根,则实数a的取值范围是 .
有一正根和一负根,则实数a的取值范围是 .
5 :解关于x的不等式 .
.
6. 已知不等式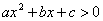 的解集为
的解集为 ,求不等式
,求不等式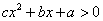 的解集.
的解集.
7.不等式|x2-3x|>4的解集是________
【提高训练】
1.设集合 ,则下列关系中成立的是( )
,则下列关系中成立的是( )
A. B.
B.  C.
C.  D.
D. 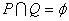
2.不等式 的解集是( )
的解集是( )
A. B.
B.  C.
C.  D.
D. 
4. 关于实数x的方程 有两个正根,则实数m的取值范围是 .
有两个正根,则实数m的取值范围是 .
【习题训练】
1.设f(x)=x2+bx+1,且f(-1)=f(3),则f(x)>0的解集是( )
A. B.R
B.R
C.{x|x≠1} D.{x|x=1
2.若不等式ax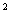 +x+a<0的解集为 Φ,则实数a的取值范围( )
+x+a<0的解集为 Φ,则实数a的取值范围( )
A a≤-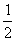 或a≥
或a≥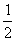 B a<
B a<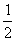 C -
C -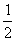 ≤a≤
≤a≤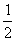 D a≥
D a≥ 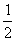
3.不等式组 的解集为( )
的解集为( )
A.(0, ) B.(
) B.( ,2) C.(
,2) C.( ,4) D.(2,4)
,4) D.(2,4)
4.关于x的方程x2+ax+a2-1=0有一正根和一负根,则a的取值范围是 .
5.不等式(x-2) ≥0的解集为________________.
≥0的解集为________________.
知识点三:简单的线性规划
1、一元一次不等式与线性规划
(1) ①若 ,
, ,则点
,则点 在直线
在直线 的上方.
的上方.
②若 ,
, ,则点
,则点 在直线
在直线 的下方.
的下方.
(2)线性规划:
【典型例题】
1.已知变量x、y满足条件则x+y的最大值是( )
A.2 B.5 C.6 D.8
2.若实数x、y满足,则的取值范围是( )
A.(0,1) B. C.(1,+∞) D.
3.已知实数x,y满足如果目标函数z=x-y的最小值为-1,则实数m等于( ) A.7 B.5 C.4 D.3
【提高训练】
1.已知变量x、y满足条件则x+y的最大值是( )
A.2 B.5 C.6 D.8
2.点P(x,y)在直线4x+3y=0上,且满足-14≤x-y≤7,则点P到坐标原点距离的取值范围是( )A.[0,5] B.[0,10] C.[5,10] D.[5,15]
3.设D是不等式组表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是________.
5. 设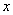 、
、 满足条件
满足条件 ,则
,则 的最小值 .
的最小值 .
【习题训练】
1.已知实数x、y满足则目标函数z=x-2y的最小值是______.
2.不等式组表示的平面区域内的整点(横坐标和纵坐标都是整数的点)共有____个.
3.若实数x,y满足不等式组则2x+3y的最小值是________.
知识点四:基本不等式
(1) ,(当且仅当
,(当且仅当 时成立等号),
时成立等号),

扩展:平均不等式:平方平均≥算术平均≥几何平均≥调和平均(a、b为正数),即
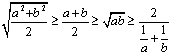 (当a = b时取等)
(当a = b时取等)
(2)对勾函数

题型一:求值域
技巧一:凑项
例1:已知 ,求函数
,求函数 的最大值。
的最大值。
技巧二:凑系数
例1. 当 时,求
时,求 的最大值。
的最大值。
技巧三: 分离
例3. 求 的值域。
的值域。
题型二:条件求值
1.若实数满足 ,则
,则 的最小值是 .
的最小值是 .
2:已知 ,且
,且 ,求
,求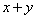 的最小值。
的最小值。
3.已知x,y为正实数,且x 2+=1,求x的最大值.
4. 已知x,y为正实数,3x+2y=10,求函数W=+的最值.
【基础训练】
1.下列结论正确的是___
A .当 且
且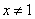 时,
时,
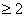 B.
B. 时,
时,
C.当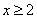 时,
时, 的最小值为2 D.
的最小值为2 D. 时,
时, 无最大值
无最大值
2.已知a>0,b>0,a+b=1,则+的取值范围是( )
A.(2,+∞) B.[2,+∞) C.(4,+∞) D.[4,+∞)
3.若x>0,y>0且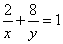 ,则xy的最小值是 ;
,则xy的最小值是 ;
4.若实数a、b满足a+b=2,则3a+3b的最小值是 ;
5.x>1,y>1且lgx+lgy=4则lgxlgy最大值为 ;
6.点(x,y)在直线x+3y-2=0上,则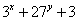 最小值为 ;
最小值为 ;
7.已知正整数a,b满足4a+b=30,使得+取最小值时,则实数对(a,b)是( )
A.(5,10) B.(6,6) C.(10,5) D.(7,2)
8. 若 ,且
,且 ,则
,则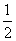 ,
, ,
,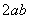 ,
, 中最大的是_______________.
中最大的是_______________.
9.设函数 则
则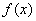 ( )
( )
A.有最大值 B.有最小值 C.是增函数 D.是减函数
10. 函数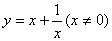 的值域为( )
的值域为( )
A.[2,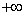 ) B.(
) B.( ,-2] C.[-2,2] D.(
,-2] C.[-2,2] D.( ,-2]
,-2] [2,
[2,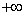 )
)
11.已知不等式 对任意正实数x,y恒成立,则正实数a的最小值为 ;
对任意正实数x,y恒成立,则正实数a的最小值为 ;
【提高训练】
1.已知 ,则
,则 的最小值 .
的最小值 .
2已知点( )在直线
)在直线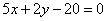 上, 其中
上, 其中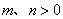 ,则
,则 ( )
( )
A.有最大值为2 B.有最小值为2 C.有最大值为1 D.有最小值为1
3. 已知非负实数 、
、 满足
满足 ,则
,则 的最大值是( )
的最大值是( )
A. B.
B.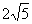 C.5 D.10
C.5 D.10
4 . 设 ,则( )
,则( )
A. 有最大值8 B.
有最大值8 B. 有最小值8 C.
有最小值8 C.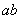 有最大值8 D.
有最大值8 D.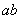 有最小值8
有最小值8
5 . 设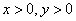 ,
, ,则
,则 ( )
( )
A.有最大值 B.有最小值
B.有最小值 C.有最大值4 D.有最小值4
C.有最大值4 D.有最小值4
6. 已知点 在直线
在直线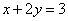 上移动,则
上移动,则 的最小值是( )
的最小值是( )
A.8 B.6 C. 3 D. 4
D. 4
7.已知x>y>0,求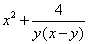 的最小值及取最小值时的x、y的值.
的最小值及取最小值时的x、y的值.
【习题训练】
1. 若 ,则
,则 的最小值是______
的最小值是______
2. 正数 满足
满足 ,则
,则 的最小值为______
的最小值为______
3. 若 ,且
,且 ,则在下列四个选项中,较大的是( ) A.
,则在下列四个选项中,较大的是( ) A.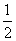 B.
B.  C.
C. D.
D. 
4.设a,b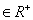 ,a+2b=3 ,则
,a+2b=3 ,则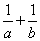 最小值是 ;
最小值是 ;
5.若x+2y=1,则2x+4y的最小值是________.
6. 若 是正数,且
是正数,且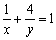 ,则
,则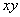 有
有
A.最大值16 B.最小值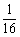 C.最小值16 D.最大值
C.最小值16 D.最大值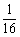
8.函数 的最小值是( )A)24 B)13 C)25 D)26
的最小值是( )A)24 B)13 C)25 D)26
知识点五:不等式的综合应用
常见、常用结论:
(1) (2)
(2)
1.不等式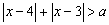 对一切实数
对一切实数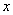 恒成立,求实数
恒成立,求实数 的取值范围_____
的取值范围_____
2.若不等式 对满足
对满足 的所有
的所有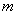 都成立,则
都成立,则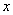 的取值范围_____
的取值范围_____
3.若不等式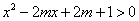 对
对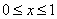 的所有实数
的所有实数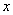 都成立,求
都成立,求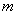 的取值范围
的取值范围
第二篇:高中数学不等式知识点经典习题
典型例题一
例1 解不等式x??2x?3?2
分析:解含有绝对值的不等式,通常是利用绝对值概念a???a(a?0),将不等式中的绝对符号去掉,转化成与?a(a?0)?
之同解的不含绝对值的不等式(组),再去求解.去绝对值符号的关键是找零点(使绝对值等于零的那个数所对应的点),将数轴分成若干段,然后从左向右逐段讨论.
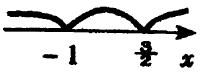
解:令x?1?0,∴ x??1,令2x?3?0,∴x?3,如图所示.2
(1)当x??1时原不等式化为?(x?1)??(2x?3)?2∴x?2与条件矛盾,无解.
33时,原不等式化为x?1??(2x?3)?2.∴ x?0,故0?x?. 22
33(3)当x?时,原不等式化为x?1?2x?3?2.∴x?6,故?x?6.综上,原不等式的解为?x0?x?6?. 22(2)当?1?x?
说明:要注意找零点去绝对值符号最好画数轴,零点分段,然后从左向右逐段讨论,这样做条理分明、不重不漏.
典型例题二
例2 求使不等式x?4?x?3?a有解的a的取值范围.
分析:此题若用讨论法,可以求解,但过程较繁;用绝对值的几何意义去求解十分简便.
解法一:将数轴分为???,3?,[3,4],(4,??)三个区间
当x?3时,原不等式变为(4?x)?(3?x)?a,x?7?a7?a?3,即a?1; 有解的条件为22
当3?x?4时,得(4?x)?(x?3)?a,即a?1;
a?7a?7?4 ∴a?1. ,有解的条件为22
以上三种情况中任一个均可满足题目要求,故求它们的并集,即仍为a?1.
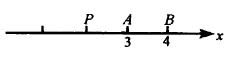
当x?4时,得(x?4)?(x?3)?a,即x?
解法二:设数x,3,4在数轴上对应的点分别为P,A,B,如图,由绝对值的几何定义,原不等式?PB?a的意义是P到A、B的距离之和小于a. 因为?1,故数轴上任一点到A、B距离之和大于(等于1),即x?4?x?3?1,故当a?1x?4?x?3?a有解.
典型例题三
例3 已知x?a???,0?y?b?,y?(0,M),求证xy???. 2M2a
分析:根据条件凑x?a,y?b. 证明:xy??xy?ya?ya??y(x?a)?a(y?b)?yx?a?a?y?b?M?
说明:这是为学习极限证明作的准备,要习惯用凑的方法. ???a???. 2M2a
典型例题四
例4 求证 a2?b2a?a?b
分析:使用分析法
证明 ∵a?0,∴只需证明a?b?a?ab,两边同除b,即只需证明2222
a2?b2
b2?ab22?aa2a2aa2a2a2aaa,即 ()?1?()?当?1时,()??()?1?()?;当?1时, bbbbbbbbbb
a?b?0,原不等式显然成立.∴原不等式成立.
说明:在绝对值不等式的证明,常用分析法.本例也可以一开始就用定理:
a2?b2
aa?bb??a??b aa22
(1)如果a?1,则a?b?0,原不等式显然成立. b
bb?1,则???b,利用不等式的传递性知a?,?a?b,∴原不等式也成立. aaa(2)如果
典型例题五
例5 求证a?b
1?a?b?a
1?a?b
1?b.
分析:本题的证法很多,下面给出一种证法:比较要证明的不等式左右两边的形式完全相同,使我们联想利用构造函数的方法,再用单调性去证明.
证明:设f(x)?x1?x?11. ??1?1?x1?x1?x
定义域为{xx?R,且x??1},f(x)分别在区间(??,?1),区间(?1,??)上是增函数. 又0?a?b?a?b,∴f(a?b)?f(a?b)即a?b
1?a?b?a?b
1?a?b?a
1?a?b?b
1?a?b?a
1?a?b
1?b
∴原不等式成立.
说明:在利用放缩法时常常会产生如下错误: ∵a?b?a?b,1?a?b?0,∴a?bababa?b. ?????1?a?b1?a?b1?a?b1?a?b1?a1?b
错误在不能保证1?a?b?1?a,1?a?b?1?b.绝对值不等式a?b?a?b在运用放缩法证明不等式时有非常重要的作用,其形式转化比较灵活.放缩要适度,要根据题目的要求,及时调整放缩的形式结构.
型例题六
22(a?1)(a?1)例6 关于实数x的不等式x?与x2?3(a?1)x?2(3a?1)?0(a?R)的解集依次为A与B,求使?22
A?B的a的取值范围.
分析:分别求出集合A、B,然后再分类讨论.
(a?1)2(a?1)2(a?1)2(a?1)2(a?1)2
?x??解:解不等式x?,?,∴A?x2a?x?a2?1,a?R. ?22222??
解不等式x2?3(a?1)x?2(3a?1)?0,[x?(3a?1)](x?2)?0. 当a??1?1时(即3a?1?2时),得B??x2?x?3a?1,a??. 3?3?
?1?1时(即3a?1?2时),得B??x3a?1?x?2,a??. 3?3?当a?
?2a?2,1A?B当a?时,要满足,必须?2故1?a?3; 3?a?1?3a?1,
当a??2a?3a?1,?a??1,1时,要满足A?B,必须? ∴a??1. ?2?1?a?1,3??2?a?1;
所以a的取值范围是a?Ra??1或1?a?3.
说明:在求满足条件A?B的a时,要注意关于a的不等式组中有没有等号,否则会导致误解. ??
典型例题七
例6 已知数列通项公式an?sinasin2asin3asinna?????对于正整数m、n,当m?n时,求证:222232n
am?an?1. 2n
分析:已知数列的通项公式是数列的前n项和,它的任意两项差还是某个数列的和,再利用不等式a1?a2???an?a1?a2???an,问题便可解决.
证明:∵m?n∴am?an?
sin(n?1)asin(n?2)asinmasin(n?1)asin(n?2)asinma????????? 2n?12n?22m2n?12n?22m
1
?1
2n?1?1
2n?2
1?1???m?21???(1?n?11m?n1?2)?1111(1?)?(0?1??1). nm?nnm?n22222n?12n?2
项是常见错误. 说明:111是以为首项,以为公比,共有m?n项的等比数列的和,误认为共有m?n?12m2n?12
正余弦函数的值域,即sin??1,cos??1,是解本题的关键.本题把不等式、三角函数、数列、n个变量的绝对值不等式问题连在一起,是一个较为典型的综合题目.如果将本题中的正弦改为余弦,不等式同样成立.
典型例题八
例8 已知f(x)?x2?x?13,x?a?1,求证:f(x)?f(a)?2(a?1)
分析:本题中给定函数f(x)和条件x?a?1,注意到要证的式子右边不含x,因此对条件x?a?1的使用可有几种选择:(1)直接用;(2)打开绝对值用a?1?x?a?1,替出x;(3)用绝对值的性质x?a?x?a?1?x?a?1进行替换.
证明:∵f(x)?x2?x?13,∴f(a)?a2?a?13,∵x?a?1,∴x?a?x?a?1. ∴x?a?1,∴f(x)?f(a)?x2?a2?a?x?(x?a)(x?a)?(x?a)?(x?a)(x?a?1)
?x?a?x?a?1?x?a??x?a?1?a?1?a?1?2(a?1),即f(x)?f(a)?2(a?1).
说明:这是绝对值和函数的综合题,这类题通常要涉及绝对值及绝对值不等式的性质等综合知识的运用.分析中对条件x?a?1使用时出现的三种可能是经常碰到的,要结合求证,灵活选用.
典型例题九
?x?0?例9 不等式组?3?x2?x的解集是( ). ??3?x2?x?
A.x0?x?2 B.x0?x?2.5
C.x0?x? D.x0?x?3 ????????
分析:本题是考查含有绝对值不等式的解法,由3?x2?x3?x?,知∴?3?x?3,又x?0,∴0?x?3,?0,3?x2?x3?x
解原不等式组实为解不等式3?x2?x?(0?x?3). 3?x2?x
解法一:不等式两边平方得:(3?x)2(2?x)2?(3?x)2(2?x)2.
∴(x2?x?6)2?(x2?x?6)2,即(x2?x?6?x2?x?6)(x2?x?6?x2?x?6)?0,
?x2?6?0∴x(6?x)?0,又0?x?3.∴? ∴0?x?.选C.
?0?x?32
解法二:∵x?0,∴可分成两种情况讨论:
3?x2?x(0?x?2).解得0?x?2. ?3?x2?x
3?xx?2(2)当x?2时,不等式组可化为(x?2),解得2?x?6. ?3?x2?x(1)当0?x?2时,不等式组化为
综合(1)、(2)得,原不等式组的解为0?x?6,选C.
说明:本题是在x?0的条件下,解一个含绝对值的分式不等式,如何去绝对值是本题的关键所在,必须注意,只有在保证两边均为非负数时,才能将不等式两边同时平方.另一种方法则是分区间讨论,从而去掉绝对值符号.当然本题还可用特殊值排除法求解.
典型例题十
例10 设二次函数f(x)?ax2?bx?c(a?0,且b?0),已知b?a,f(0)?1,f(?1)?1,f(1)?1,当x?1时,证明f(x)?5. 4
5,4分析:从a?0知,二次函数的图像是开口向上的抛物线;从x?1且f(?1)?1f(1)?1知,要求证的是f(x)?
所以抛物线的顶点一定在x轴下方,取绝对值后,图像翻到x轴上方.因此抛物线的顶点的取值非常重要,也是解这道题的关键所在.
证明:∵2b?(a?b?c)?(a?b?c)?a?b?c?a?b?c?f(1)?f(?1)?1?1?2,∴b?1.又∵b?a,∴
b4ac?b2b2bb1?c??1.∴???1.又c?f(0)?1,f(?)?, 2a4a4aa2a21b15bb2b2
?c???b?1??1?1?.而f(x)的图像为开口向上的抛物线,且x?1,∴f(?)?c??c?4a442a4a4a
?1?x?1,∴f(x)的最大值应在x?1,x??1或x??b5b处取得.∵f(1)?1,f(?1)?1,f(?)?, 2a42a
∴f(x)?5. 4
说明:本题考查了绝对值不等式的性质、二次函数的最值及分类讨论的思想和逻辑思维的能力,关键是通过对参数a,b,c的分析,确定抛物线顶点的取值范围,然后通过比较求出函数在x?1范围内的最大值.
-
高中数学人教版_必修五_不等式_知识点最完全精炼总结
20xx326一不等式淮上陌客1两实数大小的比较abab0abab0abab02不等式的性质8条性质a2b22aba2b1ab22…
-
高中数学--不等式知识点归纳和分类习题测试
必修五不等式知识点一不等式关系与不等式习题训练1下列命题中正确命题的个数是若xyz则xyyzabcdabcd0则abcd11bb1…
-
高中数学不等式知识点总结
不等式知识点总结1不等式的基本性质对称性agtbblta传递性若agtbbgtc则agtc可加性agtbacgtbc可乘性agtb…
-
高中数学知识点总结 第六章不等式
高中数学第六章不等式考试内容不等式不等式的基本性质不等式的证明不等式的解法含绝对值的不等式考试要求1理解不等式的性质及其证明2掌握…
-
高中《不等式》知识点总结
不等式知识点一不等式及其解法1一元二次不等式化标准式即二次项系数为正大于取两边小于取中间如解不等式1x2x302x2x10解1原不…
-
高二数学上学期期末复习不等式单元知识总结
一、不等式的性质1.两个实数a与b之间的大小关系?(1)a-b>0?a>b;??(2)a-b=0?a=b;??(3)a-b<0?a…
-
高中数学基本知识点汇总
高中数学基本知识点:第一:函数与导数(1)三阶段:1)学习函数概念、图象、性质。以指对函数为例,重点学习函数与反函数及单调性2)以…
-
高中数学必修1知识点、考点、题型汇总
家教资料集合与函数专题复习集合与函数知识点讲解1对于集合一定要抓住集合的代表元素及元素的确定性互异性无序性如集合AxylgxByy…
-
高中数学人教版 必修五 不等式 知识点最完全精炼总结
一不等式知识要点1两实数大小的比较abab0abab0abab02不等式的性质8条性质a2b22aba2b21ab22ab23基整…
-
高中数学知识点总结
高中数学知识点总结1对于集合一定要抓住集合的代表元素及元素的确定性互异性无序性中元素各表示什么注重借助于数轴和文氏图解集合问题空集…
-
必修五 不等式知识点总结
不等式总结一、不等式的主要性质:(1)对称性:a?b?b?a(2)传递性:a?b,b?c?a?c(3)加法法则:a?b?a?c?b…