等差数列、等比数列

【高考考情解读】 高考对本讲知识的考查主要是以下两种形式：1.以选择题、填空题的形式考查，主要利用等差、等比数列的通项公式、前n项和公式及其性质解决与项、和有关的计算问题，属于基础题；2.以解答题的形式考查，主要是等差、等比数列的定义、通项公式、前n项和公式及其性质等知识交汇综合命题，考查用数列知识分析问题、解决问题的能力，属低、中档题．

?S1， n＝1，?

1． an与Sn的关系Sn＝a1＋a2＋?＋an，an＝?

?S－S， n≥2.?nn－1

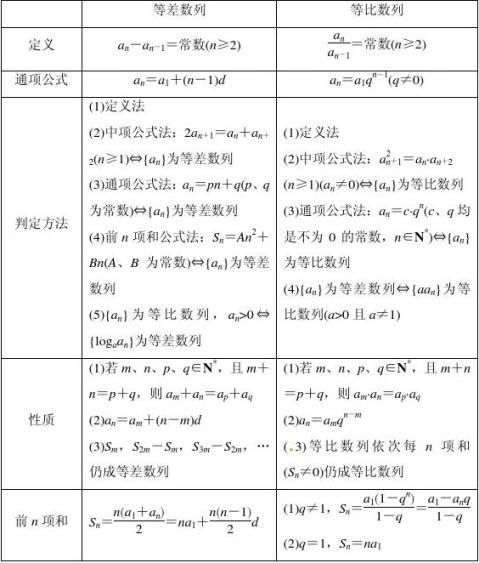
2． 等差数列和等比数列

考点一 与等差数列有关的问题

例1 在等差数列{an}中，满足3a5＝5a8，Sn是数列{an}的前n项和．

(1)若a1>0，当Sn取得最大值时，求n的值；

S－a(2)若a1＝－46，记bn＝，求bn的最小值． n

解 (1)设{an}的公差为d，则

2由3a5＝5a8，得3(a1＋4d)＝5(a1＋7d)，∴d1. 23

n?n－1??2?124∴Sn＝na1?－23a1?＝－a1n2＋a1n 22323

11441(n－12)21. 2323

∵a1>0，∴当n＝12时，Sn取得最大值．

2(2)由(1)及a1＝－46，得d(－46)＝4， 23

∴an＝－46＋(n－1)×4＝4n－50，

n?n－1?Sn＝－46n＋4＝2n2－48n. 2

Sn－an2n2－52n＋50∴bn＝＝nn

50＝2n＋52≥n2n×－52＝－32， n

50当且仅当2n＝n＝5时，等号成立．

n

故b

n的最小值为－32.

(1)在等差数列问题中其最基本的量是首项和公差，只要根据已知条件求出这两个量，其他问题就可随之而解，这就是解决等差数列问题的基本方法，其中蕴含着方程思想的运用．

(2)等差数列的性质

①若m，n，p，q∈N*，且m＋n＝p＋q，则am＋an＝ap＋aq；

②Sm，S2m－Sm，S3m－S2m，?，仍成等差数列；

am－an③am－an＝(m－n)d?d＝m，n∈N*)； m－n

aA2n－1④A，B2n－1分别为{an}，{bn}的前2n－1项的和)． bnB2n－12n－1

(3)数列{an}是等差数列的充要条件是其前n项和公式Sn＝f(n)是n的二次函数或一次函数且不含常数项，即Sn＝An2＋Bn(A2＋

B2≠

0)．

(1)(2012·浙江)设Sn是公差为d(d≠0)的无穷等差数列{an}的前n项和，则下列命题错误的是 ．．

( )

A．若d<0，则数列{Sn}有最大项

B．若数列{Sn}有最大项，则d<0

C．若数列{Sn}是递增数列，则对任意n∈N*，均有Sn>0

D．若对任意n∈N*，均有Sn>0，则数列{Sn}是递增数列

(2)(2013·课标全国Ⅰ)设等差数列{an}的前n项和为Sn，Sm－1＝－2，Sm＝0，Sm＋1＝3，则m等于

A．3 ( ) B．4 C．5 D．6

答案 (1)C (2)C

dda1n的单调性判断． 解析 (1)利用函数思想，通过讨论Sn＝n2＋?2?2

d1da1－n. 设{an}的首项为a1，则Sn＝na1＋(n－1)d＝n2＋?2?22

由二次函数性质知Sn有最大值时，则d<0，故A、B正确；

因为{Sn}为递增数列，则d>0，不妨设a1＝－1，d＝2，显然{Sn}是递增数列，但S1＝－1<0，故C错误；

对任意n∈N*，Sn均大于0时，a1>0，d>0，{Sn}必是递增数列，D正确．

(2)am＝2，am＋1＝3，故d＝1，

m?m－1?因为Sm＝0，故ma1＝0， 2

m－1故a1＝－ 2

因为am＋am＋1＝5，

故am＋am＋1＝2a1＋(2m－1)d

＝－(m－1)＋2m－1＝5，

即m＝5.

考点二 与等比数列有关的问题

例2 (1)(2012·课标全国)已知{an}为等比数列，a4＋a7＝2，a5a6＝－8，则a1＋a10等于( )

A．7 B．5 C．－5 D．－7

(2)(2012·浙江)设公比为q(q>0)的等比数列{an}的前n项和为Sn.若S2＝3a2＋2，S4＝3a4＋2，则q＝________.

3答案 (1)D (2) 2

解析 (1)利用等比数列的性质求解．

????a4＋a7＝2，?a4＝－2，?a4＝4，由?解得?或? ???aa＝aa＝－8a＝4a＝－2.?56?7?747

3???q3＝－2，?q＝－2，∴?或??a1＝1?? 1?a1＝－8，

∴a1＋a10＝a1(1＋q9)＝－7.

(2)利用等比数列的通项公式及前n项和公式求解．

S4＝S2＋a3＋a4＝3a2＋2＋a3＋a4＝3a4＋2，

将a3＝a2q，a4＝a2q2代入得，

3a2＋2＋a2q＋a2q2＝3a2q2＋2，化简得2q2－q－3＝0，

3解得q＝(q＝－1不合题意，舍去)．

2

(1)证明数列是等比数列的两个方法：①利用定义：

*用等比中项a2n＝an－1an＋1(n≥2，n∈N)． an＋1n∈N*)是常数，②利an

(2)等比数列中的五个量：a1，an，q，n，Sn可以“知三求二”．

(3){an}为等比数列，其性质如下：

①若m、n、r、s∈N*，且m＋n＝r＋s，则am·an＝ar·as； ②an＝amqnm； －

③Sn，S2n－Sn，S3n－S2n成等比数列(q≠－1)．

(4)等比数列前n项和公式

na?q＝1?，??1

Sn＝?a1?1－qn?a1－anq ＝?q≠1?.1－q?1－q

①能“知三求二”；②注意讨论公比q是否为1；③a1≠

0.

21(1)(2013·课标全国Ⅰ)若数列{an}的前n项和Sn＝an＋，则{an}的通项公式33

是an＝________.

答案 (－2)n1 －

解析 当n＝1时，a1＝1；当n≥2时，

22an＝Sn－Sn－1＝an－an－1， 33

故a－＝－2，故an＝(－2)n1. an－1

(2)(2013·湖北)已知Sn是等比数列{an}的前n项和，S4，S2，S3成等差数列，且a2＋a3＋a4＝－18.

①求数列{an}的通项公式；

②是否存在正整数n，使得Sn≥2 013？若存在，求出符合条件的所有n的集合；若不存在，说明理由．

解 ①设等比数列{an}的公比为q，则a1≠0，q≠0.由题意得

232???S2－S4＝S3－S2，?－a1q－a1q＝a1q，?即? 2??a＋a＋a＝－18.aq?1＋q＋q?＝－18，?2?134

??a1＝3，解得? ?q＝－2.?

故数列{an}的通项公式为an＝3×(－2)n1. －

3[1－?－2?n]②由①有Sn＝1－(－2)n. 1－?－2?

假设存在n，使得Sn≥2 013，

则1－(－2)n≥2 013，即(－2)n≤－2 012.

当n为偶数时，(－2)n>0.上式不成立；

当n为奇数时，(－2)n＝－2n≤－2 012，

即2n≥2 012，则n≥11.

综上，存在符合条件的正整数n，且所有这样的n的集合为{n|n＝2k＋1，k∈N，k≥5}． 考点三 等差数列、等比数列的综合应用

例3 已知等差数列{an}的公差为－1，且a2＋a7＋a12＝－6.

(1)求数列{an}的通项公式an与前n项和Sn；

(2)将数列{an}的前4项抽去其中一项后，剩下三项按原来顺序恰为等比数列{bn}的前3项，记{bn}的前n项和为Tn，若存在m∈N*，使对任意n∈N*，总有Sn<Tm＋λ恒成立，求实数λ的取值范围．

解 (1)由a2＋a7＋a12＝－6得a7＝－2，∴a1＝4，

n?9－n?∴an＝5－n，从而Sn＝2

(2)由题意知b1＝4，b2＝2，b3＝1， 设等比数列{bn}的公比为q，

b1则q＝， b12

14[1－??m]21∴Tm＝＝8[1－)m]， 121－2

1∵(m随m增加而递减， 2

∴{Tm}为递增数列，得4≤Tm<8.

n?9－n?1又Sn＝＝－(n2－9n) 22

1981n)2－]， 224

故(Sn)max＝S4＝S5＝10，

若存在m∈N*，使对任意n∈N*总有Sn<Tm＋λ，

则10<4＋λ，得λ

>6.

等差(比)数列的综合问题的常见类型及解法

(1)等差数列与等比数列交汇的问题，常用“基本量法”求解，但有时灵活地运用性质，可使运算简便．

(2)等差数列、等比数列与函数、方程、不等式等的交汇问题，求解时用等差(比)数列的相关知识，将问题转化为相应的函数、方程、不等式等问题求解即可．

已知数列{an}满足a1＝3，an＋1－3an＝3n(n∈N*)，数列{bn}满足bn＝3nan. －

(1)求证：数列{bn}是等差数列；

aaaa1S1(2)设Sn＝＋，求满足不等式<<n的值． 345128S2n4n＋2

(1)证明 由bn＝3nan得an＝3nbn， －

则an＋1＝3n1bn＋1. ＋

代入an＋1－3an＝3n中，得3n1bn＋1－3n1bn＝3n， ＋＋

1即得bn＋1－bn＝. 3

所以数列{bn}是等差数列．

(2)解 因为数列{bn}是首项为b1＝31a1＝1， －

1公差为 3

n＋21则bn＝1＋(n－1)＝ 33

则an＝3nbn＝(n＋2)×3n1， －

从而有an－3n1， n＋2

aaaa故Sn＝＋＋?＋345n＋2

＝1＋3＋3＋?＋32n－11－3n3n－1＝＝ 21－3

nS3－11则 S2n3－13＋1

由1S1111<， 128S2n41283＋14

即3<3n<127，得1<n≤4.

1S1故满足不等式n的值为2,3,4. 128S2n4

1． 在等差(比)数列中，a1，d(q)，n，an，Sn五个量中知道其中任意三个，就可以求出其他

两个．解这类问题时，一般是转化为首项a1和公差d(公比q)这两个基本量的有关运算．

2． 等差、等比数列的性质是两种数列基本规律的深刻体现，是解决等差、等比数列问题既

快捷又方便的工具，应有意识地去应用．但在应用性质时要注意性质的前提条件，有时需要进行适当变形．

3． 等差、等比数列的单调性

(1)等差数列的单调性

d>0?{an}为递增数列，Sn有最小值．

d<0?{an}为递减数列，Sn有最大值．

d＝0?{an}为常数列．

(2)等比数列的单调性

?????a1>0，?a1<0，?a1>0，?a1<0，???当或时，{an}为递增数列，当或?时，{an}为递减数?q>1??0<q<1???0<q<1??q>1

列．

4． 常用结论

S(1)若{an}，{bn}均是等差数列，Sn是{an}的前n项和，则{man＋kbn}，{仍为等差数n

列，其中m，k为常数．

(2)若{an}，{bn}均是等比数列，则{can}(c≠0)，{|an|}，{an·bn}，{manbn}(m为常数)，{a2n}，1{}等也是等比数列． an

(3)公比不为1的等比数列，其相邻两项的差也依次成等比数列，且公比不变，即a2－

a3－a2?a2－a1?qa1，a3－a2，a4－a3，?成等比数列，且公比为＝q. a2－a1a2－a1

(4)等比数列(q≠－1)中连续k项的和成等比数列，即Sk，S2k－Sk，S3k－S2k，?成等比数列，其公差为qk.

等差数列中连续k项的和成等差数列，即Sk，S2k－Sk，S3k－S2k，?成等差数列，公差为k2d.

5． 易错提醒

??S1，n＝1，(1)应用关系式an＝?时，一定要注意分n＝1，n≥2两种情况，在求出?Sn－Sn－1，n≥2?

结果后，看看这两种情况能否整合在一起．

a＋c(2)三个数a，b，c成等差数列的充要条件是b＝a，b，c成等比数列的2

必要条件是b2＝ac.

a＋a11． 已知等比数列{an}中，各项都是正数，且a1a3，2a2成等差数列，则( ) 2a6＋a7

A．1＋2

C．3＋22

答案 C

解析 记等比数列{an}的公比为q，其中q>0，

由题意知a3＝a1＋2a2，即a1q2＝a1＋2a1q.

因为a1≠0，所以有q2－2q－1＝0， 由此解得q＝2，

又q>0，所以q＝1＋2.

a8＋a9q2?a6＋a7?2所以q＝(12)2＝3＋2. a6＋a7a6＋a7

142． 已知正项等比数列{an}满足a7＝a6＋2a5，若存在两项am，an使得aman＝4a1，则的mn

最小值为

3 2

答案 A

解析 因为a7＝a6＋2a5，所以q2－q－2＝0，

解得q＝2或q＝－1(舍去)． 又amana1q＋－ B．12 D．3－22 ( ) 5B. 39 4D．不存在 ＝4a1，

所以m＋n＝6.

14114?＋(m＋n) 则?mn6?mn?

n4m131＋＋＋4?≥＝?mn?26?

n4m当且仅当，即n＝2m时，等号成立． mn

此时m＝2，n＝4.

3． 已知等差数列{an}的前n项的和为Sn，等比数列{bn}的各项均为正数，公比是q，且满

足：a1＝3，b1＝1，b2＋S2＝12，S2＝b2q.

(1)求an与bn；

an(2)设cn＝3bn－λ·2{cn}是递增数列，求λ的取值范围． 3

??q＋3＋a2＝12，解 (1)由已知可得? 2?3＋a＝q，?2

所以q2＋q－12＝0，解得q＝3或q＝－4(舍)，

从而a2＝6，所以an＝3n，bn＝3n1. －

an(2)由(1)知，cn＝3bn－λ·2＝3n－λ·2n. 3

由题意，得cn＋1>cn对任意的n∈N*恒成立，

即3n1－λ·2n1>3n－λ·2n恒成立， ＋＋

?3?n恒成立． 亦即λ·2n<2·3n恒成立，即λ?2?

3n由于函数y＝??2是增函数，

?3n?min＝2×33， 所以???2?2

故λ<3，

即λ的取值范围为(－∞，3)．

(推荐时间：60分钟)

一、选择题

1． (2013·江西)等比数列x,3x＋3,6x＋6，?的第四项等于

A．－24

答案 A

解析 由x,3x＋3,6x＋6成等比数列得，(3x＋3)2＝x(6x＋6)． 解得x＝－3或x＝－1(不合题意，舍去)．

故数列的第四项为－24.

2． (2013·课标全国Ⅱ)等比数列{an}的前n项和为Sn，已知S3＝a2＋10a1，a5＝9，则a1等

于

1 3 ( ) B．0 C．12 D．24 ( ) 1B 31C. 91D．－ 9

答案 C

解析 设等比数列{an}的公比为q，由S3＝a2＋10a1得a1＋a2＋a3＝a2＋10a1，即a3＝

19a1，q2＝9，又a5＝a1q4＝9，所以a1＝9

23． (2013·课标全国Ⅰ)设首项为1{an}的前n项和为Sn，则 ( ) 3

A．Sn＝2an－1

C．Sn＝4－3an

答案 D

21n3a1?1－q?a1－q·an解析 Sn＝＝＝＝3－2an. 11－q1－q

3n B．Sn＝3an－2 D．Sn＝3－2an

故选D.

4． 在等差数列{an}中，a5<0，a6>0且a6>|a5|，Sn是数列的前n项的和，则下列说法正确的

是 ( )

A．S1，S2，S3均小于0，S4，S5，S6?均大于0

B．S1，S2，?S5均小于0，S6，S7，?均大于0

C．S1，S2，?S9均小于0，S10，S11?均大于0

D．S1，S2，?S11均小于0，S12，S13?均大于0

答案 C

解析 由题意可知a6＋a5>0，故

S10＝?a＋a?×10?a＋a?×10＝， 22

?a1＋a9?×92a5×9而S9＝9a5<0，故选C. 22

5． 已知{an}是等差数列，Sn为其前n项和，若S21＝S4 000，O为坐标原点，点P(1，an)，

→→Q(2 011，a2 011)，则OP·OQ等于

A．2 011

答案 A

解析 由S21＝S4 000得a22＋a23＋?＋a4 000＝0，

由于a22＋a4 000＝a23＋a3 999＝?＝2a2 011，

所以a22＋a23＋?＋a4 000＝3 979a2 011＝0，

→→从而a2 011＝0，而OP·OQ＝2 011＋a2 011an＝2 011.

6． 数列{an}的首项为3，{bn}为等差数列且bn＝an＋1－an(n∈N*)．若b3＝－2，b10＝12，则

a8等于

( ) B．－2 011 C．0 D．1 ( )

A．0

答案 B

解析 因为{bn}是等差数列，且b3＝－2，b10＝12，

12－?－2?故公差d＝＝2.于是b1＝－6， 10－3

且bn＝2n－8(n∈N*)，即an＋1－an＝2n－8，

所以a8＝a7＋6＝a6＋4＋6＝a5＋2＋4＋6＝?＝

＝a1＋(－6)＋(－4)＋(－2)＋0＋2＋4＋6＝3.

二、填空题

7． (2013·广东)在等差数列{an}中，已知a3＋a8＝10，则3a5＋a7＝________.

答案 20

解析 设公差为d，则a3＋a8＝2a1＋9d＝10，∴3a5＋a7＝4a1＋18d＝2(2a1＋9d)＝20.

a3a4＋a2a618． 各项均为正数的等比数列{an}的公比q≠1，a2，a3，a1成等差数列，则＝2a2a6＋a4a5

________.

答案 5－12B．3 C．8 D．11

1＋5解析 依题意，有a3＝a1＋a2，设公比为q，则有q2－q－1＝0，所以q＝舍去负2

值)．

a3a4＋a2a6a2a4?q＋q2?15－12＝＝. 2a2a6＋a4a5a2a4?q＋q?q1＋59． 在等差数列{an}中，an>0，且a1＋a2＋?＋a10＝30，则a5·a6的最大值等于________．

答案 9

解析 由a1＋a2＋?＋a10＝30得

30a5＋a6＝＝6， 5

又an>0，∴a5·a6≤?a5＋a62?6?2?2＝?2?＝9.

110．已知数列{an}的首项为a1＝2，且an＋1＝(a1＋a2＋?＋an) (n∈N*)，记Sn为数列{an}的2

前n项和，则Sn＝________，an＝________.

2 ?n＝1?，??3?n－1 ?3答案 2×???n－2 ?n≥2?.?2????2?

111解析 由an＋1a1＋a2＋?＋an) (n∈N*)，可得an＋1＝n，所以Sn＋1－Sn＝Sn，即 222

33Sn＋1n，由此可知数列{Sn}是一个等比数列，其中首项S1＝a1＝2Sn22

2 ?n＝1?，??3n－1，由此得an＝?3＝2×??n－2 ?n≥2?.?2???2三、解答题

11．已知{an}是以a为首项，q为公比的等比数列，Sn为它的前n项和．

(1)当S1，S3，S4成等差数列时，求q的值；

(2)当Sm，Sn，Sl成等差数列时，求证：对任意自然数k，am＋k，an＋k，al＋k也成等差数列．

(1)解 由已知，得an＝aqn1，因此 －

S1＝a，S3＝a(1＋q＋q2)，S4＝a(1＋q＋q2＋q3)．

当S1，S3，S4成等差数列时，S4－S3＝S3－S1，

可得aq3＝aq＋aq2，化简得q2－q－1＝0.

5解得q＝. 2

(2)证明 若q＝1，则{an}的各项均为a，此时am＋k，an＋k，al＋k显然成等差数列． 若q≠1，由Sm，Sn，Sl成等差数列可得Sm＋Sl＝2Sn，

a?qm－1?a?ql－1?2a?qn－1?即＝，整理得qm＋ql＝2qn. q－1q－1q－1

因此，am＋k＋al＋k＝aqk1(qm＋ql)＝2aqn－＋k－1＝2an＋k.

所以am＋k，an＋k，al＋k成等差数列．

12．设数列{an}是公比大于1的等比数列，Sn为数列{an}的前n项和．已知S3＝7且a1＋3,3a2，

a3＋4构成等差数列．

(1)求数列{an}的通项公式；

(2)令bn＝ln a3n＋1，n＝1,2，?，求数列{bn}的前n项和Tn.

a＋a＋a＝7，??123

解 (1)依题意，得??a1＋3?＋?a3＋4? 3a2，?2?

解得a2＝2.

设等比数列{an}的公比为q，由a2＝2， 2可得a1＝a3＝2q. q

2又S3＝7，可知＋2＋2q＝7， q

即2q2－5q＋2＝0，

1解得q1＝2，q2＝. 2

由题意，得q>1，∴q＝2，∴a1＝1. 故数列{an}的通项公式是an＝2n1. －

(2)由于bn＝ln a3n＋1，n＝1,2，?，

由(1)得a3n＋1＝23n，

∴bn＝ln 23n＝3nln 2，

又bn＋1－bn＝3ln 2，

∴数列{bn}是等差数列．

n?b1＋bn?∴Tn＝b1＋b2＋?＋bn＝ 2

＝n?3ln 2＋3nln 2?3n?n＋1?22

13．(2013·湖北)已知等比数列{an}满足：|a2－a3|＝10，a1a2a3＝125.

(1)求数列{an}的通项公式；

111(2)是否存在正整数m，使得＋＋?＋1？若存在，求m的最小值；若不存在，a1a2am

说明理由．

解 (1)设等比数列{an}的公比为q，

33??a1q＝125，则由已知可得? 2?|a1q－a1q|＝10，?

5???a1＝3?a1＝－5，解得?或? ?q＝－1.???q＝3

5n－1－故an·3或an＝－5·(－1)n1. 3

5n－1131?n－1(2)若an＝·3，则?， 3an5?3?

?1?31故数列?a是首项为，公比为的等比数列． 53?n?

3?1m?1－m13?9??1?m?95?从而? ＝·1－<<1. a110??3??10n＝1n1－3

11－－若an＝(－5)·(－1)n1，则(－1)n1， an5

?1?1故数列?a1的等比数列， 5?n?

?11?－5，m＝2k－1?k∈N＋?，从而? ?

n＝1an??0，m＝2k?k∈N＋?.m

m故?

n＝11<1. an

m综上，对任何正整数m，总有?

n＝11an

111故不存在正整数m，使得＋?＋≥1成立． a1a2am