高中数学文科选修1-1知识点总结
第一章:命题与逻辑结构
知识点:
1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.
真命题:判断为真的语句.
假命题:判断为假的语句.
2、“若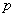 ,则
,则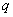 ”形式的命题中的
”形式的命题中的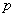 称为命题的条件,
称为命题的条件,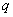 称为命题的结论.
称为命题的结论.
3、对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,则这两个命题称为互逆命题.其中一个命题称为原命题,另一个称为原命题的逆命题.
若原命题为“若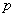 ,则
,则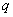 ”,它的逆命题为“若
”,它的逆命题为“若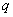 ,则
,则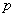 ”.
”.
4、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,则这两个命题称为互否命题.中一个命题称为原命题,另一个称为原命题的否命题.
若原命题为“若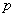 ,则
,则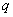 ”,则它的否命题为“若
”,则它的否命题为“若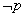 ,则
,则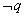 ”.
”.
5、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,则这两个命题称为互为逆否命题.其中一个命题称为原命题,另一个称为原命题的逆否命题.
若原命题为“若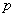 ,则
,则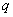 ”,则它的逆否命题为“若
”,则它的逆否命题为“若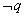 ,则
,则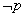 ”.
”.
6、四种命题的真假性:

四种命题的真假性之间的关系:
 两个命题互为逆否命题,它们有相同的真假性;
两个命题互为逆否命题,它们有相同的真假性;
 两个命题为互逆命题或互否命题,它们的真假性没有关系.
两个命题为互逆命题或互否命题,它们的真假性没有关系.
7、若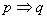 ,则
,则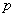 是
是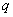 的充分条件,
的充分条件,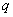 是
是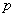 的必要条件.
的必要条件.
若 ,则
,则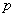 是
是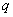 的充要条件(充分必要条件).
的充要条件(充分必要条件).
8、用联结词“且”把命题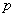 和命题
和命题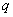 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作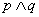 .
.
当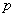 、
、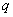 都是真命题时,
都是真命题时,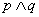 是真命题;当
是真命题;当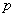 、
、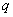 两个命题中有一个命题是假命题时,
两个命题中有一个命题是假命题时,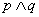 是假命题.
是假命题.
用联结词“或”把命题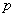 和命题
和命题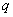 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作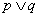 .
.
当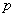 、
、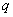 两个命题中有一个命题是真命题时,
两个命题中有一个命题是真命题时,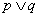 是真命题;当
是真命题;当 、
、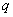 两个命题都是假命题时,
两个命题都是假命题时,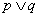 是假命题.
是假命题.
对一个命题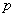 全盘否定,得到一个新命题,记作
全盘否定,得到一个新命题,记作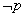 .
.
若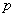 是真命题,则
是真命题,则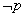 必是假命题;若
必是假命题;若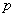 是假命题,则
是假命题,则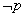 必是真命题.
必是真命题.
9、短语“对所有的”、“对任意一个”在逻辑中通常称为全称量词,用“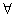 ”表示.
”表示.
含有全称量词的命题称为全称命题.
全称命题“对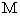 中任意一个
中任意一个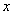 ,有
,有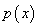 成立”,记作“
成立”,记作“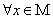 ,
,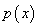 ”.
”.
短语“存在一个”、“至少有一个”在逻辑中通常称为存在量词,用“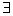 ”表示.
”表示.
含有存在量词的命题称为特称命题.
特称命题“存在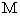 中的一个
中的一个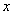 ,使
,使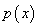 成立”,记作“
成立”,记作“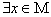 ,
,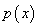 ”.
”.
10、全称命题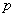 :
: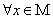 ,
,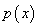 ,它的否定
,它的否定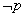 :
: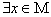 ,
,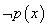 .全称命题的否定
.全称命题的否定
是特称命题.
考点:1、充要条件的判定
2、命题之间的关系
★1.命题“对任意的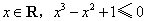 ”的否定是( )
”的否定是( )
A.不存在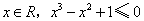 B.存在
B.存在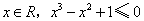
C.存在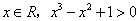 D.对任意的
D.对任意的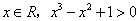
★2、给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限,在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是
(A)3 (B)2 (C)1 (D)0
★3. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“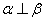 ”是“
”是“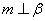 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
第二章:圆锥曲线
知识点:
1、平面内与两个定点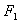 ,
,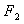 的距离之和等于常数(大于
的距离之和等于常数(大于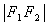 )的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
)的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
2、椭圆的几何性质:
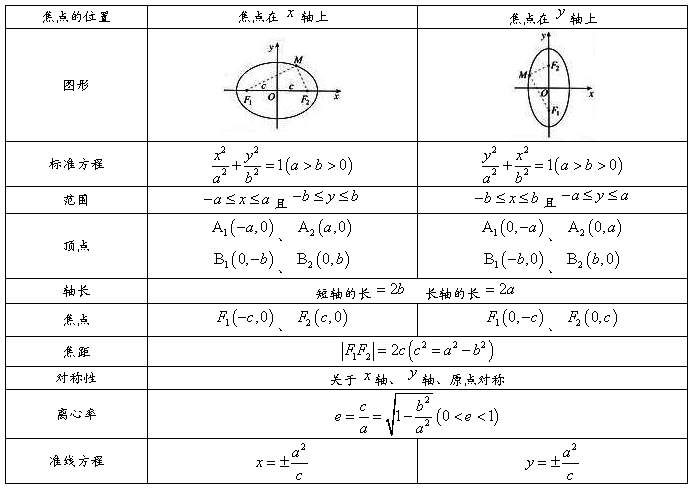
3、设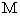 是椭圆上任一点,点
是椭圆上任一点,点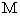 到
到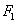 对应准线的距离为
对应准线的距离为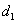 ,点
,点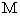 到
到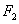 对应准线的距离为
对应准线的距离为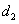 ,则
,则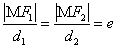 .
.
4、平面内与两个定点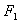 ,
,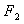 的距离之差的绝对值等于常数(小于
的距离之差的绝对值等于常数(小于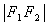 )的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
5、双曲线的几何性质:
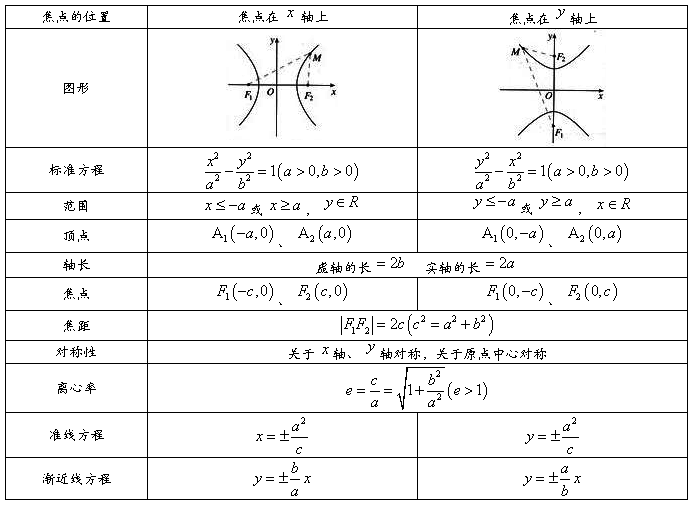
6、实轴和虚轴等长的双曲线称为等轴双曲线.
7、设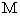 是双曲线上任一点,点
是双曲线上任一点,点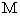 到
到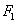 对应准线的距离为
对应准线的距离为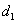 ,点
,点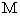 到
到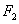 对应准线的距离为
对应准线的距离为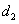 ,则
,则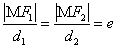 .
.
8、平面内与一个定点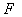 和一条定直线
和一条定直线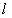 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点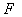 称为抛物线的焦点,定直线
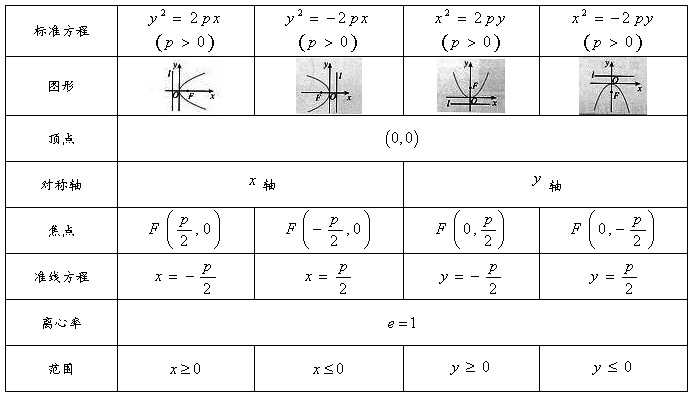
称为抛物线的焦点,定直线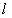 称为抛物线的准线.
称为抛物线的准线.
9、抛物线的几何性质:
10、过抛物线的焦点作垂直于对称轴且交抛物线于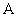 、
、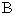 两点的线段
两点的线段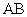 ,称为抛物线的“通径”,即
,称为抛物线的“通径”,即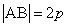 .
.
考点:1、圆锥曲线方程的求解
2、直线与圆锥曲线综合性问题
3、圆锥曲线的离心率问题
典型例题:★★1.设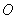 是坐标原点,
是坐标原点,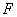 是抛物线
是抛物线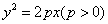 的焦点,
的焦点,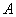 是抛物线上的一点,
是抛物线上的一点,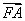 与
与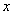 轴正向的夹角为
轴正向的夹角为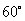 ,则
,则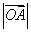 为( )
为( )
A.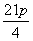 B.
B.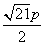 C.
C.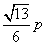 D.
D.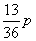
★★2.与直线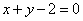 和曲线
和曲线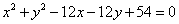 都相切的半径最小的圆的标准方程是 .
都相切的半径最小的圆的标准方程是 .
★★★3.(本小题满分14分)
已知椭圆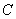 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在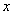 轴上,椭圆
轴上,椭圆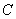 上的点到焦点距离的最大值为3,最小值为1.
上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆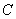 的标准方程;
的标准方程;
(2)若直线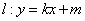 与椭圆
与椭圆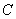 相交于
相交于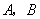 两点(
两点(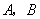 不是左右顶点),且以
不是左右顶点),且以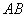 为直径的图过椭圆
为直径的图过椭圆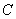 的右顶点.求证:直线
的右顶点.求证:直线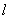 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
第三章:导数及其应用
知识点:
1、若某个问题中的函数关系用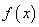 表示,问题中的变化率用式子
表示,问题中的变化率用式子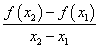
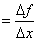 表示,则式子
表示,则式子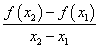 称为函数
称为函数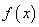 从
从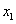 到
到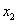 的平均变化率.
的平均变化率.
2、函数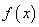 在
在 处的瞬时变化率是
处的瞬时变化率是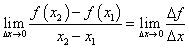 ,则称它为函数
,则称它为函数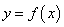 在
在 处的导数,记作
处的导数,记作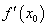 或
或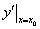 ,即
,即
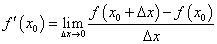 .
.
3、函数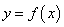 在点
在点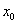 处的导数的几何意义是曲线
处的导数的几何意义是曲线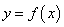 在点
在点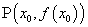 处的切线的斜率.曲线
处的切线的斜率.曲线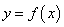 在点
在点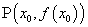 处的切线的斜率是
处的切线的斜率是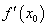 ,切线的方程为
,切线的方程为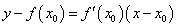 .若函数在
.若函数在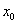 处的导数不存在,则说明斜率不存在,切线的方程为
处的导数不存在,则说明斜率不存在,切线的方程为 .
.
4、若当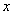 变化时,
变化时,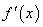 是
是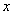 的函数,则称它为
的函数,则称它为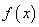 的导函数(导数),记作
的导函数(导数),记作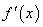 或
或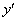 ,即
,即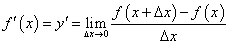 .
.
5、基本初等函数的导数公式:
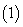 若
若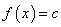 ,则
,则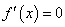 ;
;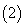 若
若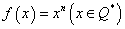 ,则
,则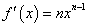 ;
;
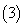 若
若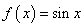 ,则
,则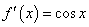 ;
;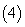 若
若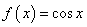 ,则
,则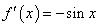 ;
;
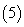 若
若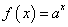 ,则
,则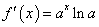 ;
;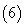 若
若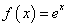 ,则
,则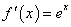 ;
;
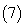 若
若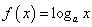 ,则
,则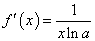 ;
;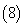 若
若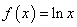 ,则
,则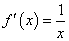 .
.
6、导数运算法则:
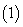
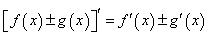 ;
;
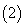
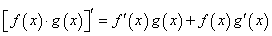 ;
;
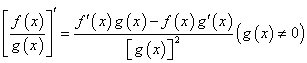 .
.
7、对于两个函数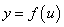 和
和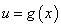 ,若通过变量
,若通过变量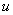 ,
,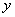 可以表示成
可以表示成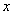 的函数,则称这个函数为函数
的函数,则称这个函数为函数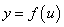 和
和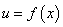 的复合函数,记作
的复合函数,记作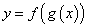 .
.
复合函数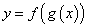 的导数与函数
的导数与函数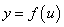 ,
,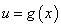 的导数间的关系是
的导数间的关系是
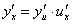 .
.
8、在某个区间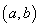 内,若
内,若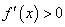 ,则函数
,则函数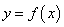 在这个区间内单调递增;若
在这个区间内单调递增;若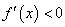 ,则函数
,则函数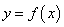 在这个区间内单调递减.
在这个区间内单调递减.
9、点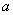 称为函数
称为函数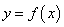 的极小值点,
的极小值点,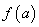 称为函数
称为函数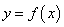 的极小值;点
的极小值;点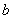 称为函数
称为函数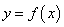 的极大值点,
的极大值点,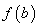 称为函数
称为函数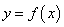 的极大值.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
的极大值.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
10、求函数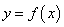 的极值的方法是:解方程
的极值的方法是:解方程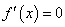 .当
.当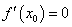 时:
时:
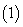 如果在
如果在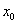 附近的左侧
附近的左侧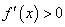 ,右侧
,右侧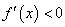 ,那么
,那么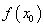 是极大值;
是极大值;
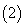 如果在
如果在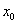 附近的左侧
附近的左侧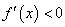 ,右侧
,右侧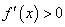 ,那么
,那么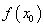 是极小值.
是极小值.
11、求函数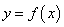 在
在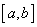 上的最大值与最小值的步骤是:
上的最大值与最小值的步骤是:
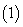 求函数
求函数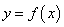 在
在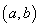 内的极值;
内的极值;
 将函数
将函数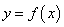 的各极值与端点处的函数值
的各极值与端点处的函数值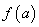 ,
,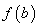 比较,其中最大的一个是最大值,最小的一个是最小值.
比较,其中最大的一个是最大值,最小的一个是最小值.
考点:1、导数在切线方程中的应用
2、导数在单调性中的应用
3、导数在极值、最值中的应用
4、导数在恒成立问题中的应用
典型例题
★1.(05全国卷Ⅰ)函数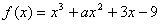 ,已知
,已知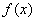 在
在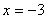 时取得极值,则
时取得极值,则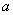 =( )
=( )
A.2 B. 3 C. 4 D.5
★2.函数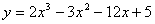 在[0,3]上的最大值与最小值分别是( )
在[0,3]上的最大值与最小值分别是( )
A.5 , - 15 B.5 , 4 C.- 4 , - 15 D.5 , - 16
★★★3.(根据04年天津卷文21改编)已知函数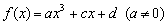 是R上的奇函数,当
是R上的奇函数,当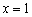 时
时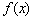 取得极值-2.
取得极值-2.
(1)试求a、c、d的值;(2)求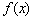 的单调区间和极大值;
的单调区间和极大值;
★★★4.(根据山东20##年文21改编)设函数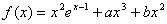 ,已知
,已知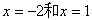 为
为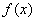 的极值点。
的极值点。
(1)求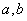 的值;
的值;
(2)讨论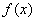 的单调性;
的单调性;
第二篇:(文科)高中数学选修1-1、1-2、4-4重要知识点
第二部分 圆锥曲线
1、平面内与两个定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹称为椭圆. 即:|MF1|?|MF2|?2a,(2a?|F1F2|)。
这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距. 2、椭圆的几何性质:
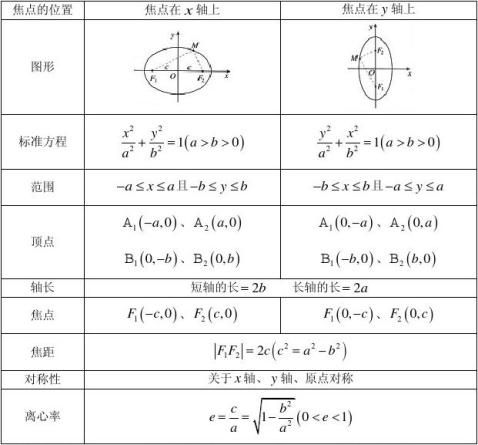

3、平面内与两个定点F1,F2的距离之差的绝对值等于常数(小于F1F2)的点的轨迹称为双曲线.即:
||MF1|?|MF2||?2a,(2a?|F1F2|)。
这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
4

56、平面内与一个定点F和一条定直线l的距离相等的点的轨迹称为抛物线.定点F称为抛物线的焦点,定直线l称为抛物线的准线.
7
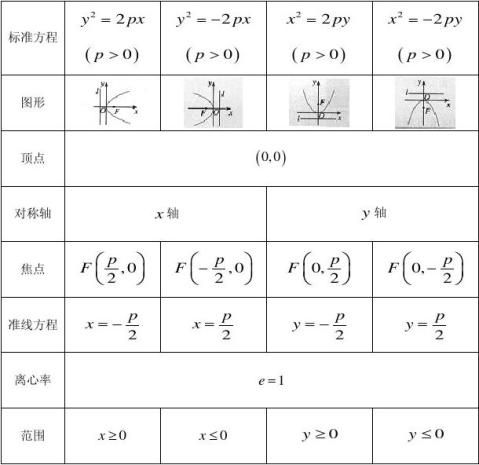
?2p.8、过抛物线的焦点作垂直于对称轴且交抛物线于?、?两点的线段??,称为抛物线的“通径”,即?
9、焦半径公式:
若点??x0,y0?在抛物线y?2px?p?0?上,焦点为F,则?F?x0?2p; 2
若点??x0,y0?在抛物线x?2py?p?0?上,焦点为F,则?F?y0?2p; 2
第三部分 导数及其应用
1、函数f?x?从x1到x2的平均变化率:f?x2??f?x1?
x2?x1
x?x0 f(x0??x)?f(x0);. ?x2、导数定义:f?x?在点x0处的导数记作y??f?(x0)?lim?x?0
3、函数y?f?x?在点x0处的导数的几何意义是曲线
4、常见函数的导数公式:
①C?0;②(x)?nx
x'x'y?f?x?在点??x0,f?x0??处的切线的斜率. n'n?1; ③(sinx)?cosx;④(cosx)??sinx; x'''⑤(a)?alna;⑥(e)?e; ⑦(logax)?x'11';⑧(lnx)? xlnax
5、导数运算法则:
?1?
?2? ???f?x??g?x????f??x??g??x?; ???f?x??g?x????f??x?g?x??f?x?g??x?;
?f?x???f??x?g?x??f?x?g??x??g?x??0????2gx??3????g?x???.
6、在某个区间?a,b?内,若f??x??0,则函数y?f?x?在这个区间内单调递增;
若f??x??0,则函数y?f?x?在这个区间内单调递减.
7、求函数y?f?x?的极值的方法是:解方程f??x??0.当f??x0??0时:
?1?如果在x0附近的左侧f??x??0,右侧f??x??0,那么f?x0?是极大值;
?2?如果在x0附近的左侧f??x??0,右侧f??x??0,那么f?x0?是极小值.
8、求函数y?f?x?在?a,b?上的最大值与最小值的步骤是:
?1?求函数y?f?x?在?a,b?内的极值;
?2?将函数y?f?x?的各极值与端点处的函数值f?a?,f?b?比较,其中最大的一个是最大值,最小的一个是最小值.
9、导数在实际问题中的应用:最优化问题。
椭圆及其性质
x2y2
2m??1表示椭圆?1.方程>0,n>0,且m≠n;a是m,n中之较大者,焦点的位置也取决于m,mn
的大小。 n
x2y21[举例] 椭圆= ??1的离心率为,则m4m2
解析:方程中4和m哪个大哪个就是a,因此要讨论;(ⅰ)若0<m<4,则a?4,b?m,∴c?4?m,222m?414?m1162=,得m=3;(ⅱ)m>4,则b2?4,a?m,∴c?m==,得m=;?4,∴em2223
16综上:m=3或m=。 3∴e=
[巩固]若方程:x2+ay2=a2 表示长轴长是短轴长的2倍的椭圆,则a的允许值的个数是 A 1个 B .2个 C.4个 D.无数个
4.研究椭圆上的点到其焦点的距离问题时,往往用定义;会推导并记住椭圆的焦半径公式。
x2y2
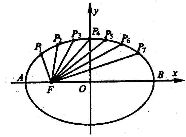
[举例1] 如图把椭圆??1的长轴AB分成8分,过 2516
每个分点作x轴的垂线交椭圆的上半部分于P,P2,……P
七个点,F是椭圆的一个焦点,则7 ?......?____________. 127
解析:P1与P7,P2与P6,P3与P5关于y轴对称,P4在y轴上,
记椭圆的另一个焦点为F/,则|P7F|=|P1F/|,|P6F|=|P2F/|,|P5F|=|P3F/|,
?......?于是|P1F|+|P1F/|+|P2F|+|P2F/|+|P3F|+|P3F/|+|P4F|=7a=35. 127
x225y28?1 [举例2] 已知A、B是椭圆2?上的两点,F是椭圆的右焦点,如果|AF|?|BF|a, AB的2225a9a2
3,则椭圆的方程 . 2
8812解析: |AF==??|?|BF|aaa, 2a?|AF|?2a?|||AF?|BF|221111555中点到椭圆左准线距离为
记AB的中点为M ,A、B、M在椭圆左准线上的射影分别为A1、B1,M1,由椭圆第二定义知:|AF1|=e|AA1|,|BF1|=e|BB1|,于是有:e(|AA1|+|BB1|)=124a,而e=55∴|AA1|+|BB1|=3a?2|MM1|=3a,又|MM1|=
3,得a=1,2
25y2
故椭圆方程为x??1。92
3.圆锥曲线的定义是求轨迹方程的重要载体之一。
[举例1]已知⊙Q:(x-1)+y=16,动⊙M过定点P(-1,0)且与⊙Q相切,则M点的轨迹方程是:
。
解释:P(-1,0)在⊙Q内,故⊙M与⊙Q内切,记:M(x,y),⊙M的半径是为r,则:|MQ|=4-r,又⊙M过点P,∴|MP|=r,于是有:|MQ|=4-|MP|,即|MQ|+|MP|=4,可见M点的轨迹是以P、Q为焦点(c=1)的椭圆,a=2。22
x?1)?(y?2),则P点的轨迹是: [举例2] 若动点P(x,y)满足|x+2y-3|=5(
A.圆 B、椭圆 C、双曲线 D、抛物线
22
-
高中数学选修1-1知识点总结
高中数学选修11知识点总结高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为…
-
高中数学选修1-1知识点归纳
高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语…
-
人教版高中数学选修1-1知识点总结(全)
高中数学选修11知识点总结第一章简单逻辑用语命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句…
-
高中数学选修1-1知识点归纳1#
高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语…
-
高中数学选修1-1知识点总结
第一章简单逻辑用语1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假命题:判断为假的语句.2、“…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…
-
人教版高中数学选修1-1知识点总结(全)
高中数学选修11知识点总结第一章简单逻辑用语命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句…
-
高中数学选修2-1知识点总结
高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的命题…
-
人教版高中数学选修2-1知识点小结
选修21知识点选修21第一章常用逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2…
-
高中数学选修1-1知识点总结
第一章简单逻辑用语1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假命题:判断为假的语句.2、“…