高中数学选修1-1知识点总结
高中数学必修五公式
第一章 三角函数
一.正弦定理: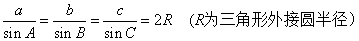

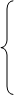
 变形:
变形: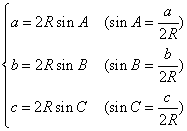 推论:
推论:
 二.余弦定理:
二.余弦定理:
三.三角形面积公式:
第二章 数列
一.等差数列: 1.定义:an+1-an=d(常数)
2.通项公式: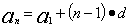 或
或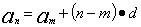
3.求和公式:
4.重要性质(1)
(2) 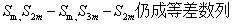
二.等比数列:1.定义: 
2.通项公式: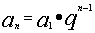 或
或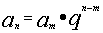
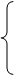 3.求和公式:
3.求和公式: 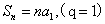

4.重要性质(1)
(2)
三.数列求和方法总结:
1.等差等比数列求和可采用求和公式(公式法).
2.非等差等比数列可考虑(分组求和法) ,(错位相减法)等转化为等差或等比数列再求和,
若不能转化为等差或等比数列则采用(拆项相消法)求和.
注意(1):若数列的通项可分成两项之和(或三项之和)则可用(分组求和法)。
(2)若一个等差数列与一个等比数列的对应相乘构成的新数列求和,采用(错位相减法).
过程:乘公比再两式错位相减
(3)若数列的通项可拆成两项之差,通过正负相消后剩有限项再求和的方法为(拆项相消法).
 常见的拆项公式:
常见的拆项公式:
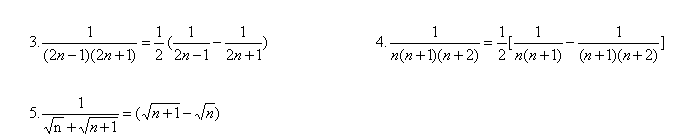
四.数列求通项公式方法总结:
1..找规律(观察法). 2..若为等差等比(公式法) 3.已知Sn,用(Sn法)即用公式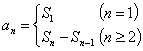
4. 叠加法 5.叠乘法等
 第三章:不等式
第三章:不等式
一.解一元二次不等式三部曲:1.化不等式为标准式ax2+bx+c>0或 ax2+bx+c<O(a>0)。
 3.根据图象写出不等式的解集.
3.根据图象写出不等式的解集.
特别的:若二次项系数a为正且有两根时写解集用口决:(不等号)大于0取两边,小于0取中间
二.分式不等式的求解通法:
(1)标准化:①右边化零,②系数化正.
(2)转 换:化为一元二次不等式(依据:两数的商与积同号)

三.二元一次不等式Ax+By+C>0(A、B不同时为0),确定其所表示的平面区域用口诀:同上异下
(注意:包含边界直线用实线,否则用虚线)
四.线性规划问题求解步骤:画(可行域)移(平行线)求(交点坐标,最优解,最值)答.
五.基本不等式: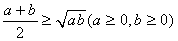 (当且仅当a=b时,等号成立)
(当且仅当a=b时,等号成立)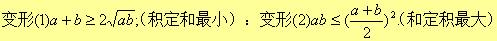
利用基本不等式求最值应用条件:一正数 二定值 三相等
旧知识回顾:1.
(1)十字相乘法:左列分解二次项系数a,右列分解常数项c,交叉相乘再相加凑成一次项系数b。
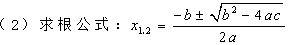
2.韦达定理:
高二数学选修2-1知识点
第一章 常用逻辑用语
1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.
真命题:判断为真的语句.假命题:判断为假的语句.
2、“若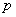 ,则
,则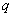 ”形式的命题中的
”形式的命题中的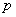 称为命题的条件,
称为命题的条件,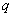 称为命题的结论.
称为命题的结论.
3.若原命题为“若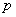 ,则
,则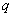 ”,它的逆命题为“若
”,它的逆命题为“若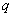 ,则
,则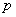 ”.
”.
它的否命题为“若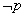 ,则
,则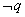 ”.
”.
它的逆否命题为“若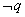 ,则
,则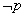 ”.
”.
4.四种命题的真假性之间的关系:
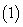 两个命题互为逆否命题,它们有相同的真假性;
两个命题互为逆否命题,它们有相同的真假性;
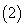 两个命题为互逆命题或互否命题,它们的真假性没有关系.
两个命题为互逆命题或互否命题,它们的真假性没有关系.
5、若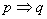 ,则
,则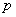 是
是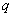 的充分条件,
的充分条件,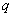 是
是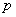 的必要条件.
的必要条件.
若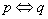 ,则
,则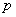 是
是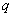 的充要条件(充分必要条件).
的充要条件(充分必要条件).
6、用联结词“且”把命题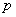 和命题
和命题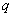 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作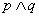 .
.
(遇假则假)
用联结词“或”把命题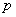 和命题
和命题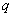 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作 .
.
(遇真则真)
对一个命题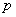 全盘否定,得到一个新命题,记作
全盘否定,得到一个新命题,记作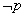 .
.
(真假相反)
7、短语“对所有的”、“对任意一个”在逻辑中通常称为全称量词,用“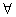 ”表示.
”表示.
含有全称量词的命题称为全称命题.
全称命题“对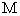 中任意一个
中任意一个 ,有
,有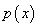 成立”,记作“
成立”,记作“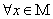 ,
,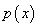 ”.
”.
短语“存在一个”、“至少有一个”在逻辑中通常称为存在量词,用“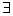 ”表示.
”表示.
含有存在量词的命题称为特称命题.
特称命题“存在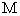 中的一个
中的一个 ,使
,使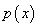 成立”,记作“
成立”,记作“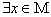 ,
,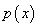 ”.
”.
8、全称命题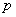 :
: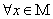 ,
,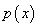 ,它的否定
,它的否定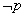 :
: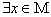 ,
, .全称命题的否定是特称命题.
.全称命题的否定是特称命题.
第二章 圆锥曲线与方程
11、平面内与两个定点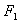 ,
, 的距离之和等于常数(大于
的距离之和等于常数(大于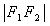 )的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
)的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
12、椭圆的几何性质:
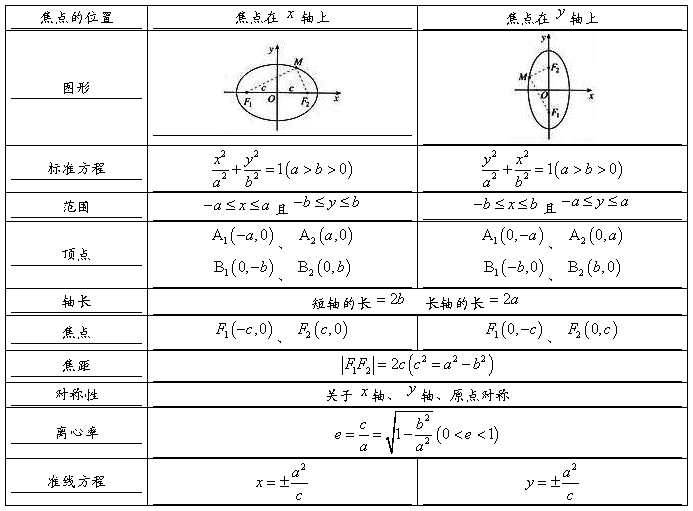
13、设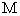 是椭圆上任一点,点
是椭圆上任一点,点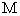 到
到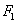 对应准线的距离为
对应准线的距离为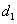 ,点
,点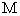 到
到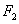 对应准线的距离为
对应准线的距离为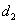 ,则
,则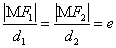 .
.
14、平面内与两个定点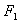 ,
, 的距离之差的绝对值等于常数(小于
的距离之差的绝对值等于常数(小于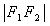 )的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
15、双曲线的几何性质:
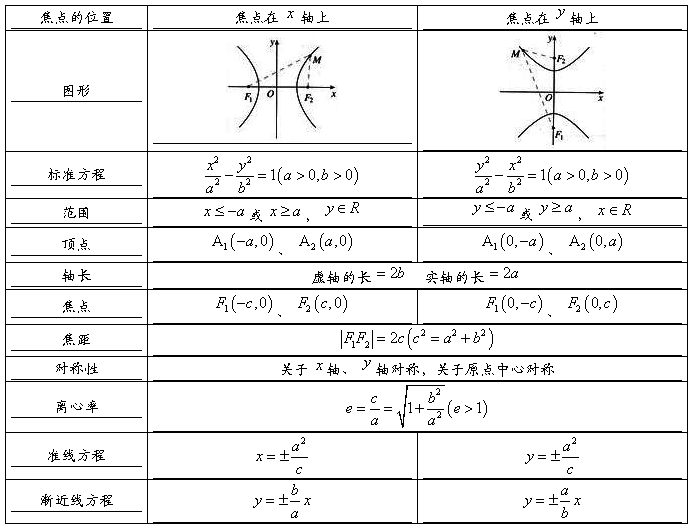
16、实轴和虚轴等长的双曲线称为等轴双曲线.( )
)
17、设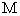 是双曲线上任一点,点
是双曲线上任一点,点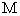 到
到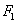 对应准线的距离为
对应准线的距离为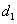 ,点
,点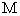 到
到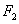 对应准线的距离为
对应准线的距离为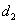 ,则
,则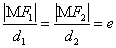 .
.
18、平面内与一个定点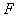 和一条定直线
和一条定直线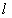 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点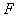 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线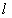 称为抛物线的准线.
称为抛物线的准线.
19、过抛物线的焦点作垂直于对称轴且交抛物线于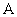 、
、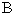 两点的线段
两点的线段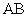 ,称为抛物线的“通径”,即
,称为抛物线的“通径”,即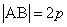 .
.
20、焦半径公式:
若点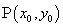 在抛物线
在抛物线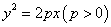 上,焦点为
上,焦点为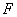 ,则
,则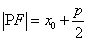 ;
;
若点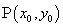 在抛物线
在抛物线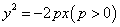 上,焦点为
上,焦点为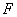 ,则
,则 ;
;
若点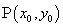 在抛物线
在抛物线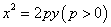 上,焦点为
上,焦点为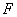 ,则
,则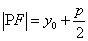 ;
;
若点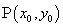 在抛物线
在抛物线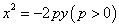 上,焦点为
上,焦点为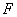 ,则
,则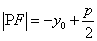 .
.
21、抛物线的几何性质:
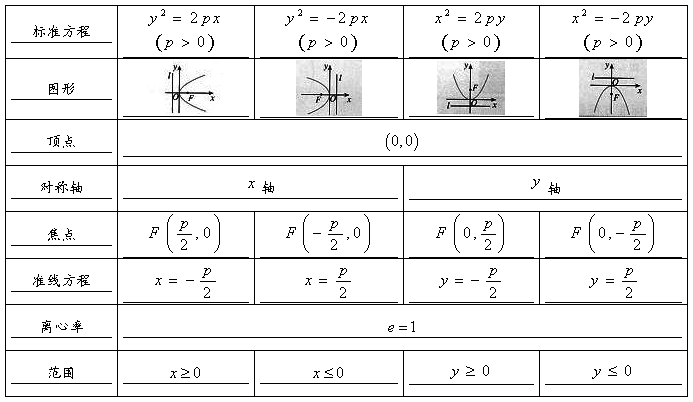
第三章导数
1.常见函数的导数公式:
(1)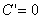 (C为常数); (2)
(C为常数); (2)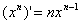 (
( );
);
(3)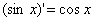 ; (4)
; (4)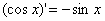 ;
;
(5)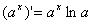 ; (6)
; (6)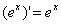 ;
;
(7)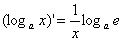 ; (8)
; (8) .
.
2.导数的运算法则:
法则1 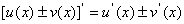 .
.
法则2 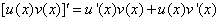 ,
, 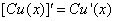 .
.
法则3 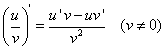 .
.
第二篇:高中数学文科选修1-2知识点总结
高中数学选修1-2知识点总结
第一章 统计案例
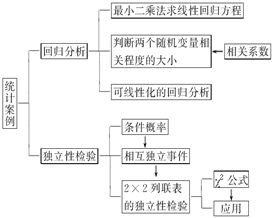 1.线性回归方程
1.线性回归方程
①变量之间的两类关系:函数关系与相关关系;
②制作散点图,判断线性相关关系
③线性回归方程: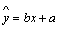 (最小二乘法)
(最小二乘法)
其中,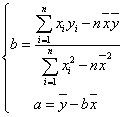
注意:线性回归直线经过定点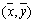 .
.
2.相关系数(判定两个变量线性相关性):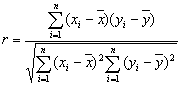
注:⑴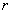 >0时,变量
>0时,变量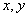 正相关;
正相关;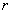 <0时,变量
<0时,变量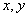 负相关;
负相关;
⑵①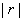 越接近于1,两个变量的线性相关性越强;②
越接近于1,两个变量的线性相关性越强;②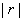 接近于0时,两个变量之间几乎不存在线性相关关系。
接近于0时,两个变量之间几乎不存在线性相关关系。
1.(2011·山东)某产品的广告费用x与销售额y的统计数据如下表:

根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为 ( ).
A.63.6万元 B.65.5万元
C.67.7万元 D.72.0万元
解析 ∵==,==42,
又=x+必过(,),∴42=×9.4+,∴=9.1.
∴线性回归方程为=9.4x+9.1.
∴当x=6时,=9.4×6+9.1=65.5(万元).
答案 B
2.(2011·江西)为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:

则y对x的线性回归方程为 ( ).
A.=x-1 B.=x+1
C.=88+x D.=176
解析 因为==176,
==176,
又y对x的线性回归方程表示的直线恒过点(,),
所以将(176,176)代入A、B、C、D中检验知选C.
答案 C
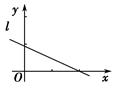 3.(2011·陕西)设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ).
3.(2011·陕西)设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ).
A.x和y的相关系数为直线l的斜率
B.x和y的相关系数在0到1之间
C.当n为偶数时,分布在l两侧的样本点的个数一定相同
D.直线l过点(,)
解析 因为相关系数是表示两个变量是否具有线性相关关系的一个值,它的
绝对值越接近1,两个变量的线性相关程度越强,所以A、B错误.C中n
为偶数时,分布在l两侧的样本点的个数可以不相同,所以C错误.根据回
归直线方程一定经过样本中心点可知D正确,所以选D.
答案 D
4.(2011·广东)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:

小李这5天的平均投篮命中率为________;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为________.
解析 小李这5天的平均投篮命中率
==0.5,
可求得小李这5天的平均打篮球时间=3.根据表中数据可求得=0.01,=
0.47,故回归直线方程为=0.47+0.01x,将x=6代入得6号打6小时篮球的
投篮命中率约为0.53.
答案 0.5 0.53
5.(2011·辽宁)调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.
解析 由题意知[0.254(x+1)+0.321]-(0.254x+0.321)=0.254.
答案 0.254
6.(2011·安徽)某地最近十年粮食需求量逐年上升,下表是部分统计数据:

(1)利用所给数据求年需求量与年份之间的回归直线方程=x+;
(2)利用(1)中所求出的直线方程预测该地20##年的粮食需求量.
解 (1)由所给数据看出,年需求量与年份之间是近似直线上升的,下面求回归直线方程.为此对数据预处理如下:

对预处理后的数据,容易算得=0,=3.2.
=
==6.5,=-b=3.
由上述计算结果,知所求回归直线方程为
-257=(x-2 006)+=6.5(x-2 006)+3.2,
即=6.5(x-2 006)+260.2. ①
(2)利用直线方程①,可预测20##年的粮食需求量为
6.5×(2012-2006)+260.2=6.5×6+260.2=299.2(万吨).
7.(2010·新课标全国)为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:

(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?
说明理由.
附:

K2=
解 (1)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估计值为=14%.
(2)K2=≈9.967.
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据
能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此
在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两
层并采用分层抽样方法比采用简单随机抽样方法更好.
8.(2010·辽宁)为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.下表1和表2分别是注射药物A和药物B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表

表2:注射药物B后皮肤疱疹面积的频数分布表

(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
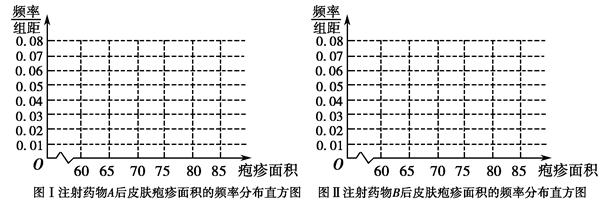
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
表3:

附:K2=
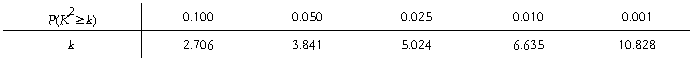
解 (1)
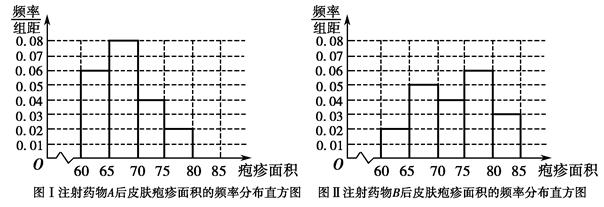
从频率分布直方图中可以看出注射药物A后皮肤疱疹面积的中位数在65至70之间,而注射药物B后皮肤疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.
(2)表3:

K2=≈24.56.
由于K2>10.828,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
-
高中数学选修1-1知识点总结
高中数学选修11知识点总结高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为…
-
高中数学选修1-1知识点归纳
高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语…
-
人教版高中数学选修1-1知识点总结(全)
高中数学选修11知识点总结第一章简单逻辑用语命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句…
-
高中数学选修1-1知识点归纳1#
高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语…
-
高中数学选修1-1知识点总结
第一章简单逻辑用语1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假命题:判断为假的语句.2、“…
-
高中数学理科选修2-2知识点总结
第一章导数及其应用一.导数概念的引入1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化率是?x?0lim…
-
高中数学人教版选修2-2导数及其应用(定积分)知识点总结
数学选修2-2导数及其应用(定积分)知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…
-
人教版高中数学选修1-1知识点总结
高中数学选修11知识点总结1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的…
-
人教版高中数学选修1-1知识点总结(全)
高中数学选修11知识点总结第一章简单逻辑用语命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句…
-
高中数学选修1-1知识点总结
第一章简单逻辑用语1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假命题:判断为假的语句.2、“…