实验报告

高等数学A（下册）数学实验

实验一：空间曲线与曲面的绘制

实验题目

利用参数方程作图，作出由下列曲面所围成的立体

（1）Z =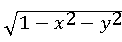, 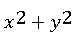= x及xOy面；

（2）z = xy, x + y – 1 = 0及z = 0.

实验方案：

(1)输入如下命令：

s1=ParametricPlot3D[{u,v,u*v},{u,-1,1},{v,-1,2},DisplayFunction®Identity];

s2=ParametricPlot3D[{1-u,u,v},{u,-1,1},{v,-1,2},DisplayFunction®Identity];

s3=ParametricPlot3D[{u,v,0},{u,-1,1},{v,-1,1},DisplayFunction®Identity];

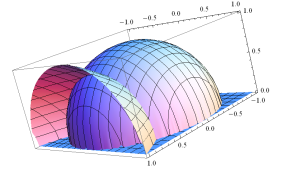
Show[s3,s2,s1,DisplayFunction®$DisplayFunction]

运行输出结果为：

(2)输入如下命令：

s1=ParametricPlot3D[{u,v,u*v},{u,-1,1},{v,-1,2},DisplayFunction®Identity];

s2=ParametricPlot3D[{1-u,u,v},{u,-1,1},{v,-1,2},DisplayFunction®Identity];

s3=ParametricPlot3D[{u,v,0},{u,-1,1},{v,-1,1},DisplayFunction®Identity];

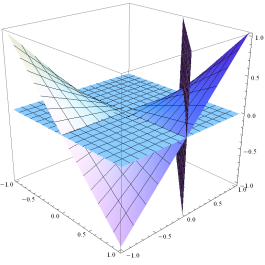
Show[s3,s2,s1,DisplayFunction®$DisplayFunction]

运行输出结果为：

实验二：无穷级数与函数逼近

实验题目

1、          观察级数的部分和序列的变化趋势，并求和。

实验方案

输入如下命令：

s[n_]:=Sum[k!/kk,{k,1,n}];

data=Table[s[n],{n,0,20}];

ListPlot[data]

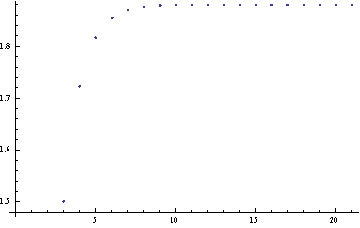
运行输出结果为：

 

输入如下命令：

  

运行输出结果为：

 

实验结论：

    由上图可知，该级数收敛，级数和大约为1.87；运行求和命令后，得近似值：1.887985.

实验题目：

2、改变函数中m及x0的数值来求函数的幂级数及观察其幂级数逼近函数的情况：

实验方案：

输入如下命令：

m=-3;f[x_]:=(1+x)^m;x0=1;

g[n_,x0_]:=D[f[x],{x,n}]/.x®x0;

s[n_,x_]:=Sum[g[k,x0]/k!*(x-x0)^k,{k,0,n}];

t=Table[s[n,x],{n,20}];

p1=Plot[Evaluate[t],{x,-1/2,1/2}];

p2=Plot[(1+x)^m,{x,-1/2,1/2},PlotStyle®RGBColor[0,0,1]];

Show[p1,p2]

运行输出结果为：

输入如下命令：

m=-2;f[x_]:=(1+x)^m;x0=2;

g[n_,x0_]:=D[f[x],{x,n}]/.x®x0;

s[n_,x_]:=Sum[g[k,x0]/k!*(x-x0)^k,{k,0,n}];

t=Table[s[n,x],{n,20}];

p1=Plot[Evaluate[t],{x,-1/2,1/2}];

p2=Plot[(1+x)^m,{x,-1/2,1/2},PlotStyle®RGBColor[0,0,1]];

Show[p1,p2]

运行输出结果为：

输入如下命令：

m=-5;f[x_]:=(1+x)^m;x0=2;

g[n_,x0_]:=D[f[x],{x,n}]/.x®x0;

s[n_,x_]:=Sum[g[k,x0]/k!*(x-x0)^k,{k,0,n}];

t=Table[s[n,x],{n,20}];

p1=Plot[Evaluate[t],{x,-1/2,1/2}];

p2=Plot[(1+x)^m,{x,-1/2,1/2},PlotStyle®RGBColor[0,0,1]];

Show[p1,p2]

运行输出结果为：

实验结论：

    由以上各图可知：当x趋近于某个值时，幂级数逼近原函数

实验题目：

3、观察函数 展成的Fourier级数的部分和逼近的情况。

实验方案：

由Fourier系数公式可得：

a0=  =+1,

an= +],

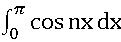bn=+],

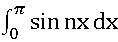f[x_]:=Which[-2Pibx＜-Pi,1,-Pibx＜0,-1,0bxbx＜2Pi,-1];

a[n_]:=(Integrate[-Cos[nx],{x,-Pi,0}]+Integrate[Cos[nx],{x,0,Pi}])/Pi;

b[n_]:=(Integrate[-Sin[nx],{x,-Pi,0}]+Integrate[Sin[nx],{x,0,Pi}])/Pi;

s[x_,n_]:=a[0]/2+Sum[a[k]*Cos[kx]+b[k]*Sin[kx],{k,1,n}];

g1=Plot[f[x],{x,-2Pi,2Pi},PlotStyle?RGBColor[0,0,1],DisplayFunction®Identity];

m=18;

For[i=1,ibm,i+=2,g2=Plot[Evaluate[s[x,i]],{x,-2Pi,2Pi},DisplayFunction®Identity];

Show[g1,g2,DisplayFunction®$DisplayFunction]]

运行输出结果为：

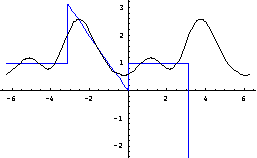
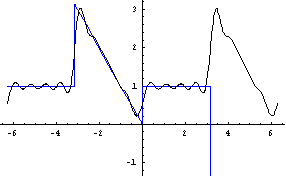
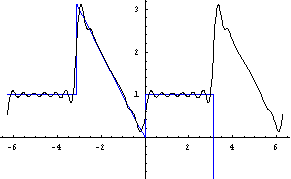
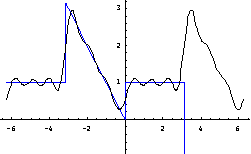
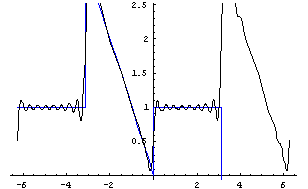
实验结论：

随着N的值的增大，曲线不断向着f(x)逼近,从最后一个图像可以看出Fourier级数的曲线已经几乎与原函数完全重合。这也再一次验证了题中周期函数可以展开为Fourier级数。

综上所述，N值越大，逼近函数的效果越好，而且Fourier级数的逼近不是一小段，而是对于函数整个定义域上的整体逼近。

实验九：最小二乘法

实验题目

1、一种合金在某种添加剂的不同浓度下进行试验，得到如下数据：

已知函数y与x的关系适合模型：，试用最小二乘法确定系数a、b、c，并求出拟合曲线。

实验方案

输入如下命令：

x={10,15,20,25,30};

y={27.0,26.8,26.5,26.3,26.1};

xy=Table[{x[[i]],y[[i]]},{i,1,5}];

ListPlot[xy,PlotStyle®PointSize[0.015]]

Q[a_,b_,c_]:=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}];

Solve[{D[Q[a,b,c],a]?0,D[Q[a,b,c],b]?0,D[Q[a,b,c],c]?0},{a,b,c}]

A={a,b,c}/.%;

l=A[[1,1]];

m=A[[1,2]];

n=A[[1,3]];

f[x_]:=l+m*x+n*x^2;

t2=Plot[f[x],{x,5,35},AxesOrigin?{5,25},DisplayFunction?Identity];

Show[t2,ListPlot[{{10,27},{15,26.8},{20,26.5},{25,26.3},{30,26.1}},PlotStyle?PointSize[0.015]]]

运行输出结果为：

{{a -＞ 27.56, b -＞ -0.0574286, c -＞ 0.000285714}}

实验结论：

求得的拟合曲线为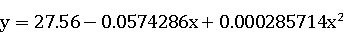：。从图中可以看出拟合程度较高。

 

第二篇：东南大学大一下高等数学实验报告

高等数学数学实验报告

实验人员：院（系） __电子_   __学号       __姓名___       __ 成绩_________

实验一

一、实验题目

观察级数的部分和序列的变化趋势，并求和；

二、实验目的和意义

   学会利用Mathematics显示级数部分和的变化趋势，并且通过实验中得到的部分和图像，对无穷级数收敛的变化趋势有更加直观的认识。

三、计算公式

=++++……++……

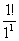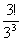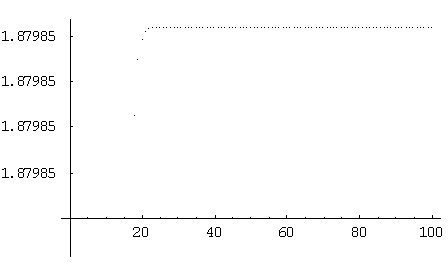
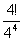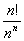四、程序设计

（1）

（2）

五、程序运行结果

（1）

（2）

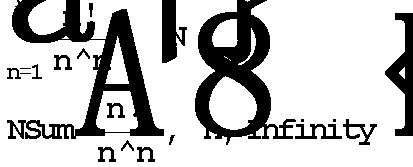
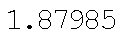
六、结果的讨论和分析

（1）一个小错误

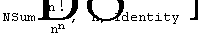
由于在输入代码时将”Infinity”错输成”Identity”，导致运行时出错，极限无法得到。

（2）结果分析

   由图像可以明显地看出图像上左侧轴上全是1.87985，是因为逼近时分度值不断变小，直至最小精确度，所以说级数的部分和趋近于1.87985。

   后来用求和功能计算级数部分和，更是可以看出其近似为1.8798，与图像所显示的值一致。

    这个实验采取散点图像法和直接的求和两种方法，共通过验证了级数和的变化趋势，收敛级数的部分和趋近于一个常数。

实验二

一、实验题目

观察函数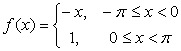展成的Fourier级数的部分和逼近的情况。

二、实验目的和意义

     通过生成Fourier级数，利用其图像研究级数的部分和逼近。同时利用幂级数的部分和来对函数进行逼近和函数值的近似计算，进而研究Fourier级数对周期函数的逼近。

三、计算公式

设f(x)是以2T为周期的周期函数，在任一周期内，f(x)除有限个第一类间断点外都连续，并且只有有限个极值点，则f(x)可以展开为Fourier级数：

，

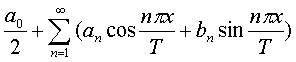其中

且Fourier级数在任一点处收敛于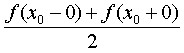

四、程序设计

五、程序运行结果

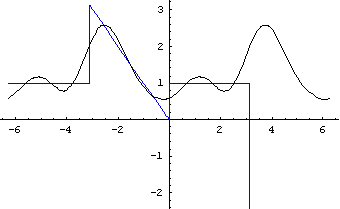
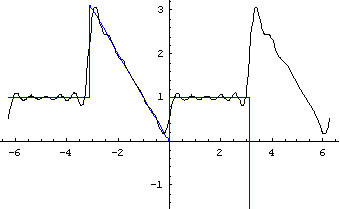
六、结果的讨论和分析

    题中函数显然在任一周期内，f(x)除了有限个第一类间断点外都连续，并且只有有限个极值点，所以函数可以展开成Fourier级数。

再次观察函数逼近的图像，可以发现当N的值小的时候，逼近曲线接近于三角函数曲线，与原来的分段函数相去甚远。但是随着N的值的增大，曲线不断向着f(x)逼近,从最后一个图像可以看出Fourier级数的曲线已经几乎与原函数完全重合。这也再一次验证了题中周期函数可以展开为Fourier级数。

综上所述，N值越大，逼近函数的效果越好，而且Fourier级数的逼近不是一小段，而是对于函数整个定义域上的整体逼近。