数 值 分 析 作 业

数值分析之曲线拟合

1. 问题的提出

在化工设计及化工模拟算中，需要大量的物性参数及各种设备参数。这些参数有些可以通过计算得到，但大量的参数还是要通过实验测量得到。实验测得的常常是一组离散数据序列，如果序列，含有不可避免的误差，或者无法同时满足某特定的函数，这时通常通过数据拟合来完成，曲线拟合往往并不需要曲线通过给定的所有数据点（即待定参数的数量比给定的数据点的数量少），而只要求用曲线（函数）近似代替给定的列表函数，时，其误差在某种度量意义下最小。如：要求所作的逼近函数最优地靠近样点，即向量的误差或距离最小。按所求的逼近函数和样点之间误差最小原则作 “最优”标准的构造的逼近函数，称为拟合函数。

2. 曲线拟合的方法及拟合标准

 2.1 曲线拟合的方法

设在上给出一组数据

，

以及一组线性无关的函数族，，其中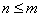。问题是要在曲线族

 

中寻找一个合适的曲线以某种原则使其无限逼近数据点所表示的函数关系。

现在定义如下：

若曲线

使

成立，这就是最小二乘逼近，这种方法称为曲线拟合的最小二乘法。可知，若要求曲线，就是按条件求出系数。

求最小二乘法的方法：

设

     

     

     

就等价于

即成立。

其中  

 2.2 拟合标准

拟合曲线与数据点之间的误差或距离有不同的定义方法：

   1. 用各点误差的绝对值的和表示：

                 

2. 用各点误差按绝对值的最大值表示：

3. 用各点误差的平方和表示：

            

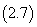
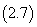式中的称为均方误差。

3. 曲线拟合的几种类型

 3.1 单变量拟合

1. 线性拟合

给定一组数据，作拟合曲线，均方误差为

由数学知识可知，的极小值需要满足

整理得到拟合曲线满足的方程

式称为拟合曲线的法方程。可用消元法或克莱姆方法求解。

2. 二次拟合函数

给定一组数据，用二次项式函数拟合这组数据。

设，作出拟合函数与数据序列的均方误差表达式

由数学知识可知，的极小值满足

整理上式得二次多项式函数拟合需满足的条件方程

解此方程得到在均方误差最小意义下的拟合函数。式称为多项式拟合的法方程，法方程的系数矩阵是对称的。当拟合多项式时，法方程的系数矩阵是病态的，在用通常的有有迭代法求解线性方程时会发散，在计算中要采用一些特殊的算法以保护解的准确性。

3.2 多变量曲线拟合

上面所述的几种曲线拟合的方法只涉及单变量函数的曲线拟合，但实际在化工实验数据处理及模型参数拟合时，通常会碰到多变量的参数拟合问题。其中最典型的例子就是传热实验中的努赛尔数、雷诺数及普朗特数之间的拟合问题：

    给定一组数据序列，，用一次多项式函数拟合这组数据。

    设，作出拟合函数与数据序列的均方误差

由多元函数的极值原理，的极小值满足

整理上式得二次多项式函数拟合需满足的条件方程

通过求解方程就可以得到多变量函数线性拟合时的参数，由于方程不是线性方程，可能通过对方程两边同时取对数，得到以下线性方程

只要作如下变量代换

 

    

   

并将实验数据代入法方程就可能求出方程中的系数。

4. 实例分析

   正庚烷和甲苯构成的二元溶液，溶液和组成的实验结果如表4-1所示。其中表示正庚烷的摩尔分数，表示混合热。

表4-1 正庚烷的含量（摩尔分数）与混合热的关系

从散点图（图4-1）看，是一条抛物线，可以用抛物线方程来拟合。

按照抛物线方程：

如果我们在曲线上任取一点，则有

两式相减，得：

             

             

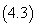
令，

则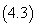式变为：，可以看出，这与之间呈线性关系。

因此，可用对作图，看它是否存在线性关系，并用相关系数检验的方法做定量检验。

我们选定其中一组数据作业，于是计算出：

用对作图，果然得到一条直线。见图4-2。

   

计算的相关系数为：

    由此证明，我们确实把曲线变成了直线。这样，就可以先求出直线方程的两个常数，再写出描述这条曲线的经验方程式：

                          

                         

                         

    即         

将实验数据代入，求出计算的值，结果见表4-2。

表4-2 经验方程的计算值与实验值的比较

如果想使曲线拟合的效果更好，可在方程中增加更高次的项：

                 

5. 小结

曲线拟合涉及的一个基本问题就是，最佳拟合意味着什么？怎样由实验测得的数据设计和确定“最贴近”的拟合曲线，其关键在于选择合适的曲线类型或模型类型，有时根据专业知识和工作经验即可确定拟合曲线类型；在对拟合曲线一无所知的情况下，不妨先绘制数据的粗略图形，或许可从中观测出拟合曲线的类型；更一般地，对数据进行多种曲线拟合的拟合，并算均方误差，用数学实验的方法找出在最小二乘法意义下的误差最小的拟合函数。

附录：

1. 用MATLAB编程软件绘制图4-1正庚烷的含量与混合热的关系，对应的MATLAB程序如下：

x=[0.05 0.11 0.17 0.18 0.28 0.31 0.33 0.39 0.44 0.53 0.54 0.62 0.71 0.82];

y=[0.13 0.23 0.32 0.35 0.44 0.47 0.48 0.51 0.52 0.51 0.50 0.48 0.42 0.28];

plot(x,y,'-*r')

axis([0.0,1,0.0,0.6]);

title('图4-1 正庚烷的含量与混合热的关系')

xlabel('正庚烷的摩尔分数')

ylabel('混合热kJ/mol')

2. 用MATLAB编程软件绘制图4-2正庚烷的含量与混合热的线性图，对应的MATLAB程序如下：

x=[0.05 0.11 0.17 0.18 0.28 0.31 0.33 0.39 0.44 0.53 0.54 0.62 0.71 0.82];

y=[1.00 0.88 0.75 0.65 0.50 0.38 0.36 0.20 0.00 -0.11 -0.20 -0.22 -0.37 -0.63];

plot(x,y,'-*r')

axis([0.0,1.0,-1.0,1.2]);

title('图4-2 正庚烷的含量与混合热的线性图')

xlabel('正庚烷的含量')

ylabel('y=(y-y0)/(x-x0)，x0=0.44;y0=0.52')

 

第二篇：《数值分析》课程设计报告范文

课程设计报告

课程设计题目： 非线性方程求解      

 20##年 11月 27 日

题目：

用二分法，简单迭代法、牛顿迭代法以及弦截法求非线性方程

误差不超过10-4，输出迭代次数，初始值和根的近似值。

一、摘要

在matlab环境下运用熟悉的计算机编程语言结合二分法、简单迭代法、牛顿迭代法以及弦截法求解非线性方程，在运行完程序后，对运行结果做出了各方面的分析和比较。

最终得出二分法迭代次数最多，需14次，而简单迭代法、牛顿迭代法以及弦截法的迭代次数都较少，只需4—5次。由于方程有多个解，所以当赋的初始值不同或给定的区间不同时，根的近似值也会有所不同。

二、设计目的

用熟悉的计算机语言编程，上机完成用二分法、简单迭代法、牛顿迭代法以及弦截法求解非线性方程，掌握各种方法的理论依据及求解思路，了解各种迭代方法的异同。

三、理论基础

二分法：

二分法就是将方程根所在的区间平分为两个小区间，再判断根属于哪个小区间；把有根的小区间再平分为二，再判断根所在的更小的区间，对分；重复这一过程，最后求出所要的近似值。

简单迭代法：

简单迭代法是将方程化为一个等价的方程：

从而构成序列：

即给定一个初值，由（2）可算得，再将带入（2）的右端，又可得，…。我们{}为迭代序列，而称（1）式中的为迭代函数，（2）为迭代格式。如果连续，迭代序列{}收敛于，则就是方程（1）的解。事实上，又，亦即：

或

所以，如果迭代序列收敛，总能收敛于原方程的解。实际计算中，无穷过程不可能实现，只迭代到一定程度，取作为原方程的近似根。

牛顿迭代法：

设已知方程的一个近似根，把在处做泰勒展开，

若取前两项来近似代替（称为的线性化），则得近似的线性方程：

设，解之得。取作为原方程的近似根，即，一般地，再重复用上述方法得：。一般地，有迭代公式

上式称为求解的牛顿迭代公式。

弦截法：

假设方程在区间[a,b]上有唯一根，在区间[a,b]内的曲线上任取两点作弦，用此弦与轴的交点横坐标作为方程根的近似值。按此方法进行迭代计算，直到满足精度要求为止。

单点弦法：为避免导数的计算，用平均变化率

来替代迭代公式中的导数，于是得到：

按此公式进行迭代计算就称单点弦截法。按(3)式求得的实际上是弦AB与轴交点的横坐标，下一步再以点()和()作弦交轴得等等。每次作新的弦都以()作为一个端点，只有一个端点不断更换，故名为单点弦截法。

四、程序代码及运算结果

function y=f(x)

y=sin(x)-x.^2/2;

二分法：

clear;clc;

a=-2;b=1;

chushizhi1=-2

chushizhi2=1

kg=10^(-4);

for k=0:20

if f(a)*f(b)＞0

   x=error

else

    if f(a)*f(b)==0

       if f(a)==0

            a,k;

        else b,k;

       end

    else m=(a+b)/2;

    if abs(a-b)

            jinsijie=m

            diedaicishu=k-1

            break

    else

        if f(a)*f(m)＞0

            a=m;

    else b=m;

        end

        k=k+1;

    end

        end

    end

end

运行结果

chushizhi1 =-2

chushizhi2 =1

jinsijie =1.5259e-005

diedaicishu =14

简单迭代法：

  x(1)=1

for k=1:12

      x(k+1)=asin((x(k).^2)/2);

      if (abs(x(k+1)-x(k)))＜0.0001

          x(k+1)

          k

          break

      end

end

运行结果

jinsijie =9.9887e-010

diedaicishu =5

chushizhi =1

牛顿迭代法：

syms  x

y=diff(sin(x)-x.^2/2,x)

y = cos(x)-x

function y=p(x)

y=cos(x)-x;

x(1)=-1;

for k=1:20

    if p(x(k))~=0

        x(k+1)=x(k)-f(x(k))./p(x(k));

        if (abs(x(k+1)-x(k)))＜0.0001

            jinsijie=x(k+1)

            diedaicishu=k

            break

        end

    end

end

chushizhi=x(1)

运行结果

Jinsijie = -2.6055e-010

diedaicishu =4

chushizhi =-1

弦解法：

x(1)=-0.1;

x(2)=0.2;

for k=1:7

    if (f(x(k))-f(x(1)))~=0

        x(k+1)=x(k)-f(x(k))*(x(k)-x(1))/(f(x(k))-f(x(1)));

        f(x(k+1))

        if (abs(x(k+1)-x(k)))＜0.0001

            jinsijie=x(k+1)

            diedaicishu=k

            break

        end

    end

end

chushizhi1=x(1)

chushizhi2=x(2)

运行结果

jinsijie =1.0816e-006

diedaicishu =5

chushizhi1 =-0.1000

chushizhi2 =0.2000

五、结果分析

根据二分法求解非线性方程根的原理，将所求方程根所在的区间平分为两个小区间，在判断根属于哪个小区间；把有根的小区间再平分为二，再判断根所在的更小的区间，对分；重复这一过程，最后求出所要的近似值。当所分的小区间的间距越小的时候，得出的方程根结果就越精确，其原因就是所分的小区间间距越小，则就越接近方程等于0的根。所以最后的结果的精度越高，得到的误差越小；而对于简单迭代法，只有在满足一定条件的情况下，才能求解出在区间上有唯一根，使迭代序列收敛于。根据牛顿迭代法的原理，求解出非线性方程根的结果可以看出，牛顿迭代法具有平方收敛的速度，所以在迭代过程中只要迭代几次就会得到比较精确的解，并不像简单迭代法，需要迭代多次才能解出较为精确的结果，但是用牛顿迭代法求解时选定的初值要接近方程的解，否则可能得不到收敛的结果。同时，牛顿迭代法计算量也会相对较大些。单点弦截法，用选定的两个初值点所对应的函数值连接作弦，用此弦与轴的交点横坐标作为方程根的近似值。按此方法进行迭代计算，直到满足精度要求为止。

六、设计心得

这次数值分析课程设计我们虽然只经历了一周，但是受益匪浅。在刚开始拿到题目时，我们提出很多问题，3个人各有自己的想法，产生了分歧。但经过这一周的时间和体验下来，我们学到的不仅是课本知识，还有团队和合作精神。现在想来，也许学校安排的课程设计有着它更深层的意义，它不仅仅让我们综合那些理论知识来运用到设计和创新，还让我们知道了一个团队凝聚在一起是所能发挥出的巨大潜能！

在这次课程设计中，我们运用到了以前所学的专业课知识，如：用二分法、牛顿迭代法、弦截法、matlab汇编语言等。虽然过去都将这些知识用于解题中，未有独立应用过它们，但在学习的过程中带着问题去学我发现效率很高。设计过程，好比我们的成长历程，常有一些不如意，难免会遇到各种各样的问题。这也激发了我今后努力学习的兴趣，通过这次设计，我懂得了学习的重要性，了解到理论知识与实践结合的重要意义，学会了坚持、耐心和努力，这将为自己今后的学习和工作打下基础。

七、参考文献

[1]奚梅成。数值分析方法【M】。合肥：中国科技技术大学出版社，2007.

[2]薛毅。数值分析与实验【M】。北京：北京理工大学出版社，2005.

[3]汪卉琴，刘目楼。数值分析【M】。北京：冶金工业出版社，2004.

[4]丁丽娟，程杞元。数值计算方法【M】。北京：北京理工大学出版社，2005.

[5]李庆扬，易大义，王能超。现代数值分析。北京：高等教育出版社，1995.

[6]薛定宇，陈阳泉。高等应用数学问题的MATLAB求解。北京：清华大学出版社，2008.