考研.数学 线性代数总结2
线性代数部分—矩阵理论
一、矩阵基本概念
1、矩阵的定义—形如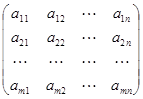 ,称为矩阵
,称为矩阵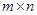 ,记为
,记为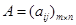 。
。
特殊矩阵有
(1)零矩阵—所有元素皆为零的矩阵称为零矩阵。
(2)方阵—行数和列数都相等的矩阵称为方阵。
(3)单位矩阵—主对角线上元素皆为1其余元素皆为零的矩阵称为单位矩阵。
(4)对称矩阵—元素关于主对角线成轴对称的矩阵称为对称矩阵。
2、同型矩阵—行数和列数相同的矩阵称为同型矩阵。若两个矩阵同型且对应元素相同,称两个矩阵相等。
3、矩阵运算
(1)矩阵加、减法:
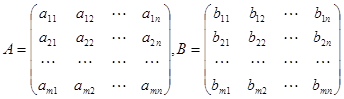 ,则
,则
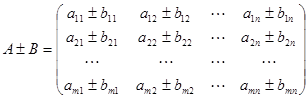 。
。
(2)数与矩阵之积:
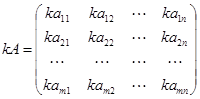 。
。
(3)矩阵与矩阵之积:
设 ,则
,则
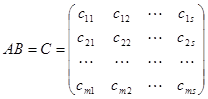 ,
,
其中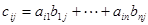 (
(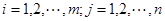 )
)
【注解】
(1)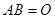 不一定有
不一定有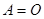 或
或 。
。
(2)矩阵乘法没有交换律。
(3)含方阵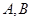 的矩阵多项式可象普通多项式一样因式分解的充分必要条件是
的矩阵多项式可象普通多项式一样因式分解的充分必要条件是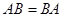 。
。
(4)设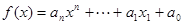 ,则定义
,则定义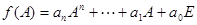 ,且关于矩阵
,且关于矩阵 的矩阵多项式可因式分解。
的矩阵多项式可因式分解。
二、方程组的矩阵形式及解的概况
方程组的基本形式为
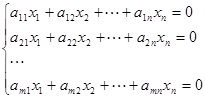 (1)
(1)
称(1)为齐次线性方程组。
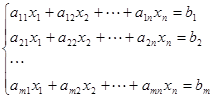 (2)
(2)
称(2)为非齐线性方程组。
令 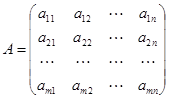 ,
, ,
, ,则(1)、(2)可分别表示为矩阵形式:
,则(1)、(2)可分别表示为矩阵形式:
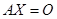 (1)
(1)
及
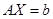 (2)
(2)
对方程组(1):
【例题1】讨论方程组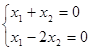 解的情况,并分析原因。
解的情况,并分析原因。
【例题2】讨论方程组 解的情况,并分析原因。
解的情况,并分析原因。
对方程组(2):
【例题1】讨论方程组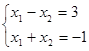 解的情况,并分析原因。
解的情况,并分析原因。
【例题2】讨论方程组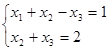 解的情况,并分析原因。
解的情况,并分析原因。
【例题3】讨论方程组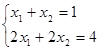 解的情况,并分析原因。
解的情况,并分析原因。
三、矩阵问题的产生
初一数学问题:解一元一次方程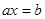
情形一:当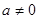 时,
时,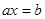 两边同时乘以
两边同时乘以 得
得 ,于是
,于是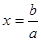 ;
;
情形二:当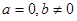 时,方程
时,方程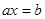 无解;
无解;
情形三:当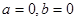 时,方程
时,方程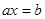 有无数个解。
有无数个解。
线性方程组的类似问题:讨论方程组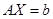 的解
的解
情形一: 是
是 阶方阵,且存在
阶方阵,且存在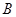 ,使得
,使得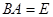
由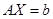 两边左乘
两边左乘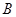 得
得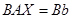 ,于是
,于是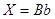 ;
;
情形二: 虽然是
虽然是 阶矩阵,但不存在
阶矩阵,但不存在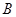 ,使得
,使得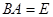
方程组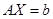 是否有解及解的情况;
是否有解及解的情况;
情形三: 是
是 矩阵,且
矩阵,且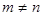
方程组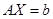 是否有解及解的情况。
是否有解及解的情况。
【注解】
(1)第一种解的情况产生矩阵的第一个核心问题—矩阵的逆阵。
(2)第二、三两种情形产生矩阵的另一个核心问题—矩阵的秩。
四、矩阵两大核心为题
(一)逆阵
1、定义—设 为
为 阶矩阵,若存在
阶矩阵,若存在 阶矩阵
阶矩阵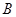 ,使得
,使得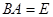 ,则称
,则称 为可逆矩阵,
为可逆矩阵,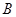 称为
称为 的逆矩阵,记为
的逆矩阵,记为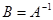 。
。
2、两个问题
【问题1】 给定一个 阶矩阵
阶矩阵 ,是否存在可逆矩阵(事实上不存在可逆矩阵的矩阵大量存在)?
,是否存在可逆矩阵(事实上不存在可逆矩阵的矩阵大量存在)?
【问题2】 若 阶矩阵
阶矩阵 可逆(即逆矩阵存在),如何求其逆矩阵?
可逆(即逆矩阵存在),如何求其逆矩阵?
3、矩阵可逆充分必要条件
定理设 为
为 阶矩阵,则
阶矩阵,则 可逆的充分必要条件是
可逆的充分必要条件是 。
。
4、求矩阵逆阵的方法
方法一:伴随矩阵法(略)
方法二:初等变换法
第一步 方程组的三种同解变形
(1)对调两个方程的位置方程组的解不变;
(2)某个方程两边同乘以一个非零常数方程组的解不变;
(3)某个方程的倍数加到另一个方程方程组的解不变。
第二步 矩阵的三种初等行变换
(1)对调矩阵的两行;
(2)矩阵的某行同乘以一个非零常数;
(3)矩阵某行的倍数加到另一行。
第三步 三种初等矩阵
(1)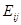 —单位矩阵的
—单位矩阵的 行与
行与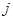 行对调或者
行对调或者 列与
列与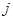 列对调所得的矩阵。
列对调所得的矩阵。
性质:1)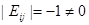 ; 2)
; 2)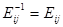 或者
或者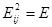 ;
;
3) 为将
为将 的
的 行与
行与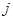 行对调所得的矩阵,
行对调所得的矩阵,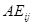 为将
为将 的
的 列与
列与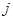 列对调所得的矩阵。
列对调所得的矩阵。
(2)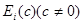 —单位矩阵的
—单位矩阵的 行乘以
行乘以 或单位矩阵的
或单位矩阵的 列乘以
列乘以 。
。
性质:1) ; 2)
; 2) ;
;
3)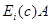 为将
为将 的
的 行乘以非零常数
行乘以非零常数 所得到的矩阵,
所得到的矩阵,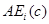 为将
为将 的
的 列乘以非零常数
列乘以非零常数 所得到的矩阵。
所得到的矩阵。
(3)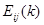 —单位矩阵的
—单位矩阵的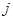 行的
行的 倍加到
倍加到 行或者单位矩阵的
行或者单位矩阵的 列的
列的 倍加到
倍加到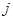 列所得到的矩阵。
列所得到的矩阵。
性质: 1) ; 2)
; 2)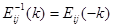 ;
;
3) 为将
为将 的
的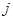 行的
行的 倍加到
倍加到 行所得到的矩阵,
行所得到的矩阵, 为将
为将 的
的 列的
列的 倍加到
倍加到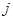 列所得到的矩阵。
列所得到的矩阵。
第四步 三个问题
【问题1】设 为
为 阶可逆矩阵,
阶可逆矩阵, 能够经过有限次初等行变换化为单位矩阵?
能够经过有限次初等行变换化为单位矩阵?
【问题2】 设 为
为 阶不可逆矩阵,
阶不可逆矩阵, 能够经过有限次初等行变换化为
能够经过有限次初等行变换化为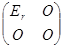 ?
?
【问题3】 设 为
为 阶不可逆矩阵,
阶不可逆矩阵, 能够经过有限次初等变换化为
能够经过有限次初等变换化为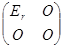 ?
?
第五步 初等变换法求逆阵及两个相关的定理
定理(初等变换法求逆阵)设 为
为 阶可逆矩阵,则
阶可逆矩阵,则 可以经过有限次初等行变换化为初等矩阵。
可以经过有限次初等行变换化为初等矩阵。
(二)矩阵的秩(记住:在方程组中矩阵的秩本质上就是约束条件)
1、定义—设 为
为 矩阵,若
矩阵,若 存在一个
存在一个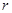 阶非零子式,但所有的
阶非零子式,但所有的 阶子式(如果有)都是零,则
阶子式(如果有)都是零,则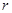 称为
称为 的秩,记为
的秩,记为 。
。
【注解】
(1)任何矩阵的秩都既不超过其行数也不超过其列数。设 为
为 矩阵,则
矩阵,则
 。
。
(2)设 为
为 阶矩阵,若
阶矩阵,若 ,则
,则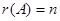 ,称
,称 为满秩矩阵。矩阵可逆、满秩及非奇异等价。
为满秩矩阵。矩阵可逆、满秩及非奇异等价。
2、矩阵秩的求法
将矩阵进行初等行变换阶梯化所得的非零行数即为矩阵的秩。
【注解】
(1)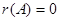 的充分必要条件是
的充分必要条件是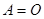 。
。
(2)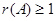 的充分必要条件是
的充分必要条件是 。
。
(3)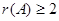 的充分必要条件是
的充分必要条件是 至少有两行不成比例。
至少有两行不成比例。
(4)设 ,则
,则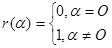 。
。
3、矩阵秩的性质
(1) 。
。
(2)设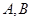 为同型矩阵,则
为同型矩阵,则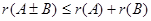 。
。
(3)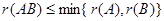 ,等价于
,等价于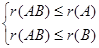 。
。
(4)设 为
为 矩阵,
矩阵,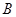 为
为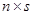 矩阵,且
矩阵,且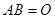 ,则
,则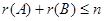 。
。
(5)设 为
为 矩阵,
矩阵,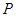 为
为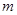 阶可逆阵,
阶可逆阵,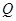 为
为 阶可逆阵,则有
阶可逆阵,则有
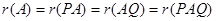 。
。
【矩阵秩例题】
【例题1】设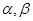 皆为三维列向量,
皆为三维列向量, ,证明:
,证明: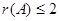 。
。
【例题2】设 为
为 阶可逆阵,证明
阶可逆阵,证明 的逆阵是唯一的。
的逆阵是唯一的。
【例题3】设 为
为 矩阵,
矩阵,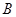 为
为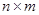 矩阵,其中
矩阵,其中 ,且
,且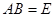 ,证明:
,证明: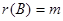 。
。
【例题4】设 为
为 阶矩阵,且
阶矩阵,且 ,证明:
,证明: 。
。
第二篇:考研数学线性代数必备结论
1、行列式
1.  行列式共有
行列式共有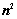 个元素,展开后有
个元素,展开后有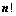 项,可分解为
项,可分解为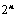 行列式;
行列式;
2. 代数余子式的性质:
①、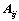 和
和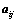 的大小无关;
的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0;
③、某行(列)的元素乘以该行(列)元素的代数余子式为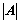 ;
;
3. 代数余子式和余子式的关系:
4. 设 行列式
行列式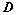 :
:
将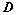 上、下翻转或左右翻转,所得行列式为
上、下翻转或左右翻转,所得行列式为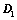 ,则
,则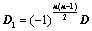 ;
;
将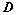 顺时针或逆时针旋转
顺时针或逆时针旋转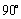 ,所得行列式为
,所得行列式为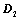 ,则
,则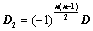 ;
;
将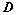 主对角线翻转后(转置),所得行列式为
主对角线翻转后(转置),所得行列式为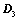 ,则
,则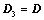 ;
;
将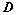 主副角线翻转后,所得行列式为
主副角线翻转后,所得行列式为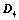 ,则
,则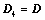 ;
;
5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
②、副对角行列式:副对角元素的乘积 ;
;
③、上、下三角行列式(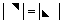 ):主对角元素的乘积;
):主对角元素的乘积;
④、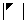 和
和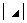 :副对角元素的乘积
:副对角元素的乘积 ;
;
⑤、拉普拉斯展开式: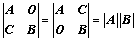 、
、
⑥、范德蒙行列式:大指标减小指标的连乘积;
⑦、特征值;
6. 对于 阶行列式
阶行列式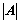 ,恒有:
,恒有: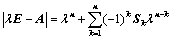 ,其中
,其中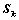 为
为 阶主子式;
阶主子式;
7. 证明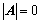 的方法:
的方法:
①、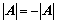 ;
;
②、反证法;
③、构造齐次方程组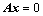 ,证明其有非零解;
,证明其有非零解;
④、利用秩,证明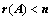 ;
;
⑤、证明0是其特征值;
2、矩阵
1.  是
是 阶可逆矩阵:
阶可逆矩阵:

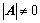 (是非奇异矩阵);
(是非奇异矩阵);

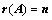 (是满秩矩阵)
(是满秩矩阵)

 的行(列)向量组线性无关;
的行(列)向量组线性无关;
 齐次方程组
齐次方程组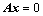 有非零解;
有非零解;

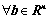 ,
, 总有唯一解;
总有唯一解;

 与
与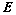 等价;
等价;

 可表示成若干个初等矩阵的乘积;
可表示成若干个初等矩阵的乘积;

 的特征值全不为0;
的特征值全不为0;

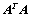 是正定矩阵;
是正定矩阵;

 的行(列)向量组是
的行(列)向量组是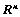 的一组基;
的一组基;

 是
是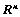 中某两组基的过渡矩阵;
中某两组基的过渡矩阵;
2. 对于 阶矩阵
阶矩阵 :
: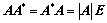 无条件恒成立;
无条件恒成立;
3. 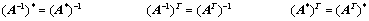

4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;
5. 关于分块矩阵的重要结论,其中均 、
、 可逆:
可逆:
若 ,则:
,则:
Ⅰ、 ;
;
Ⅱ、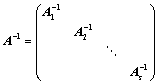 ;
;
②、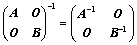 ;(主对角分块)
;(主对角分块)
③、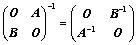 ;(副对角分块)
;(副对角分块)
④、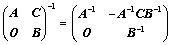 ;(拉普拉斯)
;(拉普拉斯)
⑤、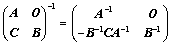 ;(拉普拉斯)
;(拉普拉斯)
3、矩阵的初等变换与线性方程组
1. 一个 矩阵
矩阵 ,总可经过初等变换化为标准形,其标准形是唯一确定的:
,总可经过初等变换化为标准形,其标准形是唯一确定的: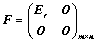 ;
;
等价类:所有与 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
对于同型矩阵 、
、 ,若
,若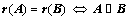 ;
;
2. 行最简形矩阵:
①、只能通过初等行变换获得;
②、每行首个非0元素必须为1;
③、每行首个非0元素所在列的其他元素必须为0;
3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)
①、 若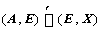 ,则
,则 可逆,且
可逆,且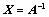 ;
;
②、对矩阵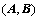 做初等行变化,当
做初等行变化,当 变为
变为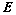 时,
时, 就变成
就变成 ,即:
,即: ;
;
③、求解线形方程组:对于 个未知数
个未知数 个方程
个方程 ,如果
,如果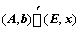 ,则
,则 可逆,且
可逆,且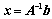 ;
;
4. 初等矩阵和对角矩阵的概念:
①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;
②、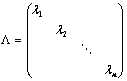 ,左乘矩阵
,左乘矩阵 ,
,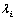 乘
乘 的各行元素;右乘,
的各行元素;右乘,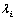 乘
乘 的各列元素;
的各列元素;
③、对调两行或两列,符号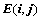 ,且
,且 ,例如:
,例如: ;
;
④、倍乘某行或某列,符号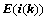 ,且
,且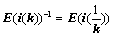 ,例如:
,例如: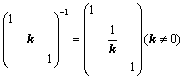 ;
;
⑤、倍加某行或某列,符号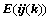 ,且
,且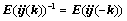 ,如:
,如: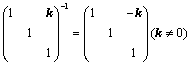 ;
;
5. 矩阵秩的基本性质:
①、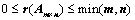 ;
;
②、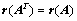 ;
;
③、若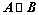 ,则
,则 ;
;
④、若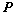 、
、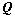 可逆,则
可逆,则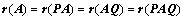 ;(可逆矩阵不影响矩阵的秩)
;(可逆矩阵不影响矩阵的秩)
⑤、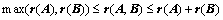 ;(※)
;(※)
⑥、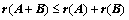 ;(※)
;(※)
⑦、 ;(※)
;(※)
⑧、如果 是
是 矩阵,
矩阵, 是
是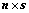 矩阵,且
矩阵,且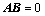 ,则:(※)
,则:(※)
Ⅰ、 的列向量全部是齐次方程组
的列向量全部是齐次方程组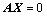 解(转置运算后的结论);
解(转置运算后的结论);
Ⅱ、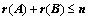
⑨、若 、
、 均为
均为 阶方阵,则
阶方阵,则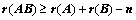 ;
;
6. 三种特殊矩阵的方幂:
①、秩为1的矩阵:一定可以分解为列矩阵(向量)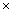 行矩阵(向量)的形式,再采用结合律;
行矩阵(向量)的形式,再采用结合律;
②、型如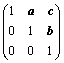 的矩阵:利用二项展开式;
的矩阵:利用二项展开式;
二项展开式: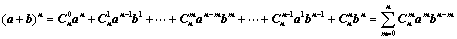 ;
;
注:Ⅰ、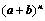 展开后有
展开后有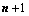 项;
项;
Ⅱ、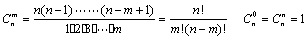
Ⅲ、组合的性质: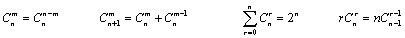 ;
;
③、利用特征值和相似对角化:
7. 伴随矩阵:
①、伴随矩阵的秩: ;
;
②、伴随矩阵的特征值: ;
;
③、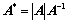 、
、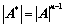
8. 关于 矩阵秩的描述:
矩阵秩的描述:
①、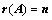 ,
, 中有
中有 阶子式不为0,
阶子式不为0,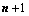 阶子式全部为0;(两句话)
阶子式全部为0;(两句话)
②、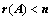 ,
, 中有
中有 阶子式全部为0;
阶子式全部为0;
③、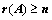 ,
, 中有
中有 阶子式不为0;
阶子式不为0;
9. 线性方程组: ,其中
,其中 为
为 矩阵,则:
矩阵,则:
①、 与方程的个数相同,即方程组
与方程的个数相同,即方程组 有
有 个方程;
个方程;
②、 与方程组得未知数个数相同,方程组
与方程组得未知数个数相同,方程组 为
为 元方程;
元方程;
10. 线性方程组 的求解:
的求解:
①、对增广矩阵 进行初等行变换(只能使用初等行变换);
进行初等行变换(只能使用初等行变换);
②、齐次解为对应齐次方程组的解;
③、特解:自由变量赋初值后求得;
11. 由 个未知数
个未知数 个方程的方程组构成
个方程的方程组构成 元线性方程:
元线性方程:
①、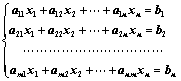 ;
;
②、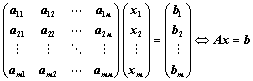 (向量方程,
(向量方程, 为
为 矩阵,
矩阵, 个方程,
个方程, 个未知数)
个未知数)
③、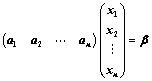 (全部按列分块,其中
(全部按列分块,其中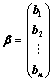 );
);
④、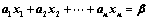 (线性表出)
(线性表出)
⑤、有解的充要条件: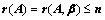 (
( 为未知数的个数或维数)
为未知数的个数或维数)
4、向量组的线性相关性
1.  个
个 维列向量所组成的向量组
维列向量所组成的向量组 :
: 构成
构成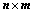 矩阵
矩阵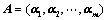 ;
;
 个
个 维行向量所组成的向量组
维行向量所组成的向量组 :
: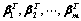 构成
构成 矩阵
矩阵 ;
;
含有有限个向量的有序向量组与矩阵一一对应;
2. ①、向量组的线性相关、无关 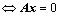 有、无非零解;(齐次线性方程组)
有、无非零解;(齐次线性方程组)
②、向量的线性表出  是否有解;(线性方程组)
是否有解;(线性方程组)
③、向量组的相互线性表示 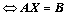 是否有解;(矩阵方程)
是否有解;(矩阵方程)
3. 矩阵 与
与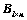 行向量组等价的充分必要条件是:齐次方程组
行向量组等价的充分必要条件是:齐次方程组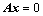 和
和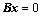 同解;(
同解;( 例14)
例14)
4. 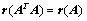 ;(
;( 例15)
例15)
5.  维向量线性相关的几何意义:
维向量线性相关的几何意义:
①、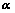 线性相关
线性相关 
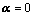 ;
;
②、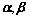 线性相关
线性相关 
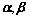 坐标成比例或共线(平行);
坐标成比例或共线(平行);
③、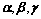 线性相关
线性相关 
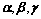 共面;
共面;
6. 线性相关与无关的两套定理:
若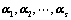 线性相关,则
线性相关,则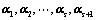 必线性相关;
必线性相关;
若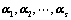 线性无关,则
线性无关,则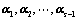 必线性无关;(向量的个数加加减减,二者为对偶)
必线性无关;(向量的个数加加减减,二者为对偶)
若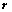 维向量组
维向量组 的每个向量上添上
的每个向量上添上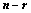 个分量,构成
个分量,构成 维向量组
维向量组 :
:
若 线性无关,则
线性无关,则 也线性无关;反之若
也线性无关;反之若 线性相关,则
线性相关,则 也线性相关;(向量组的维数加加减减)
也线性相关;(向量组的维数加加减减)
简言之:无关组延长后仍无关,反之,不确定;
7. 向量组 (个数为
(个数为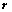 )能由向量组
)能由向量组 (个数为
(个数为 )线性表示,且
)线性表示,且 线性无关,则
线性无关,则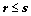 (二版
(二版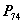 定理7);
定理7);
向量组 能由向量组
能由向量组 线性表示,则
线性表示,则 ;(
;(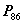 定理3)
定理3)
向量组 能由向量组
能由向量组 线性表示
线性表示
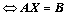 有解;
有解;
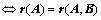 (
( 定理2)
定理2)
向量组 能由向量组
能由向量组 等价
等价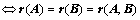 (
( 定理2推论)
定理2推论)
8. 方阵 可逆
可逆 存在有限个初等矩阵
存在有限个初等矩阵 ,使
,使 ;
;
①、矩阵行等价: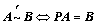 (左乘,
(左乘,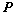 可逆)
可逆)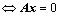 与
与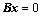 同解
同解
②、矩阵列等价: (右乘,
(右乘,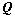 可逆);
可逆);
③、矩阵等价: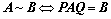 (
(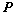 、
、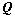 可逆);
可逆);
9. 对于矩阵 与
与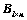 :
:
①、若 与
与 行等价,则
行等价,则 与
与 的行秩相等;
的行秩相等;
②、若 与
与 行等价,则
行等价,则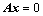 与
与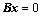 同解,且
同解,且 与
与 的任何对应的列向量组具有相同的线性相关性;
的任何对应的列向量组具有相同的线性相关性;
③、矩阵的初等变换不改变矩阵的秩;
④、矩阵 的行秩等于列秩;
的行秩等于列秩;
10. 若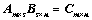 ,则:
,则:
①、 的列向量组能由
的列向量组能由 的列向量组线性表示,
的列向量组线性表示, 为系数矩阵;
为系数矩阵;
②、 的行向量组能由
的行向量组能由 的行向量组线性表示,
的行向量组线性表示,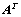 为系数矩阵;(转置)
为系数矩阵;(转置)
11. 齐次方程组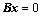 的解一定是
的解一定是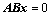 的解,考试中可以直接作为定理使用,而无需证明;
的解,考试中可以直接作为定理使用,而无需证明;
①、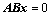 只有零解
只有零解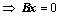 只有零解;
只有零解;
②、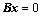 有非零解
有非零解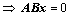 一定存在非零解;
一定存在非零解;
12. 设向量组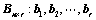 可由向量组
可由向量组 线性表示为:(
线性表示为:( 题19结论)
题19结论)
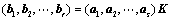 (
(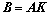 )
)
其中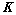 为
为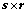 ,且
,且 线性无关,则
线性无关,则 组线性无关
组线性无关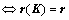 ;(
;( 与
与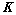 的列向量组具有相同线性相关性)
的列向量组具有相同线性相关性)
(必要性: ;充分性:反证法)
;充分性:反证法)
注:当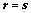 时,
时,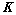 为方阵,可当作定理使用;
为方阵,可当作定理使用;
13. ①、对矩阵 ,存在
,存在 ,
,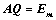
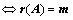 、
、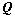 的列向量线性无关;(
的列向量线性无关;(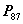 )
)
②、对矩阵 ,存在
,存在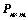 ,
,
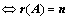 、
、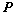 的行向量线性无关;
的行向量线性无关;
14. 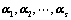 线性相关
线性相关
 存在一组不全为0的数
存在一组不全为0的数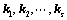 ,使得
,使得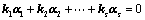 成立;(定义)
成立;(定义)

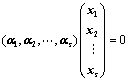 有非零解,即
有非零解,即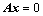 有非零解;
有非零解;

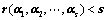 ,系数矩阵的秩小于未知数的个数;
,系数矩阵的秩小于未知数的个数;
15. 设 的矩阵
的矩阵 的秩为
的秩为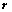 ,则
,则 元齐次线性方程组
元齐次线性方程组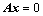 的解集
的解集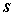 的秩为:
的秩为: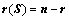 ;
;
16. 若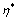 为
为 的一个解,
的一个解, 为
为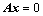 的一个基础解系,则
的一个基础解系,则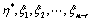 线性无关;(
线性无关;(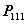 题33结论)
题33结论)
5、相似矩阵和二次型
1. 正交矩阵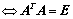 或
或 (定义),性质:
(定义),性质:
①、 的列向量都是单位向量,且两两正交,即
的列向量都是单位向量,且两两正交,即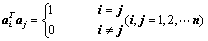 ;
;
②、若 为正交矩阵,则
为正交矩阵,则 也为正交阵,且
也为正交阵,且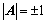 ;
;
③、若 、
、 正交阵,则
正交阵,则 也是正交阵;
也是正交阵;
注意:求解正交阵,千万不要忘记施密特正交化和单位化;
2. 施密特正交化: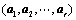
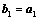 ;
;


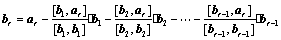 ;
;
3. 对于普通方阵,不同特征值对应的特征向量线性无关;
对于实对称阵,不同特征值对应的特征向量正交;
4. ①、 与
与 等价
等价 
 经过初等变换得到
经过初等变换得到 ;
;
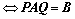 ,
,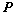 、
、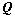 可逆;
可逆;
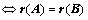 ,
, 、
、 同型;
同型;
②、 与
与 合同
合同 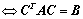 ,其中可逆;
,其中可逆;
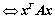 与
与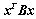 有相同的正、负惯性指数;
有相同的正、负惯性指数;
③、 与
与 相似
相似 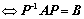 ;
;
5. 相似一定合同、合同未必相似;
若 为正交矩阵,则
为正交矩阵,则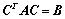
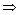
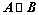 ,(合同、相似的约束条件不同,相似的更严格);
,(合同、相似的约束条件不同,相似的更严格);
6.  为对称阵,则
为对称阵,则 为二次型矩阵;
为二次型矩阵;
7.  元二次型
元二次型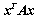 为正定:
为正定:
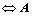 的正惯性指数为
的正惯性指数为 ;
;
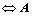 与
与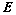 合同,即存在可逆矩阵
合同,即存在可逆矩阵 ,使
,使 ;
;
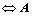 的所有特征值均为正数;
的所有特征值均为正数;
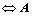 的各阶顺序主子式均大于0;
的各阶顺序主子式均大于0;
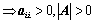 ;(必要条件)
;(必要条件)
-
考研线性代数知识点全面总结
线性代数复习提纲第一章行列式1行列式的定义用n2个元素aij组成的记号称为n阶行列式1它表示所有可能的取自不同行不同列的n个元素乘…
-
考研线性代数大总结
1行列式1n行列式共有n2个元素展开后有n项可分解为2n行列式2代数余子式的性质Aij和aij的大小无关某行列的元素乘以其它行列元…
-
考研数学之线性代数讲义(考点知识点+概念定理总结)
收集自网络,不以任何盈利为目的。欢迎考研的同学,下载学习。线性代数讲义目录第一讲基本概念线性方程组矩阵与向量初等变换和阶梯形矩阵线…
-
考研线性代数知识点全面总结
线性代数复习提纲第一章行列式值不是矩阵1行列式的定义用n个元素a组成的记号称为n阶行列式2ij1它表示所有可能的取自不同行不同列的…
-
20xx考研线性代数知识点总结(免费)
1行列式1n行列式共有n2个元素展开后有n项可分解为2n行列式2代数余子式的性质Aij和aij的大小无关某行列的元素乘以其它行列元…
-
20xx考研数学线性代数重点内容和典型题型总结
线性代数在考研数学中占有重要地位,必须予以高度重视.线性代数试题的特点比较突出,以计算题为主,证明题为辅,因此,万学海文数学考研辅…
-
20xx考研数学 线性代数超级总结-2
⑨r(A?B)≤r(A)?r(B)max?r(A),r(B)?≤r(A,B)≤r(A)?r(B)p教材70⑩r??A?OO??O?…
-
线性代数中必考知识点归纳总结
20xx年线性代数必考的知识点1、行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、…
-
考研数学复习小结(概率论与数理统计初步、线性代数)
考研数学复习小结(概率论与数理统计初步、线性代数)(20xx年x月x日15:48:19海文学校阅读:)浏览器不支持嵌入式框架,或被…
-
考研线代重点内容和典型题型总结
凯程考研集训营为学生引路为学员服务考研线代重点内容和典型题型总结线性代数在考研数学中占有重要地位必须予以高度重视线性代数试题的特点…
-
线性代数总结
第一部分:基本要求(计算方面)四阶行列式的计算;N阶特殊行列式的计算(如有行和、列和相等);矩阵的运算(包括加、减、数乘、乘法、转…