高数下册总结
高数(下)小结
一、微分方程复习要点
解微分方程时,先要判断一下方程是属于什么类型,然后按所属类型的相应解法
求出其通解.
一阶微分方程的解法小结:

二阶微分方程的解法小结:

齐次方程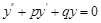 的通解
的通解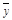 为:
为:

非齐次方程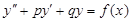 的特解
的特解 的形式为:
的形式为:

主要:
一阶1、可分离变量方程、线性微分方程的求解;
2、二阶常系数齐次线性微分方程的求解;
3、二阶常系数非齐次线性微分方程的特解
二、多元函数微分学复习要点
一、偏导数的求法
1、显函数的偏导数的求法
在求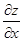 时,应将
时,应将 看作常量,对
看作常量,对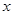 求导,在求
求导,在求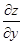 时,应将
时,应将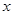 看作常量,对
看作常量,对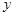 求导,所运用的是一元函数的求导法则与求导公式.
求导,所运用的是一元函数的求导法则与求导公式.
2、复合函数的偏导数的求法
设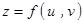 ,
,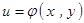 ,
,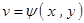 ,则
,则
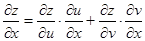 ,
,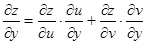
几种特殊情况:
1)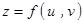 ,
,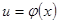 ,
,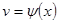 ,则
,则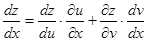
2)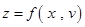 ,
, ,则
,则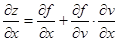 ,
,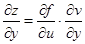
3)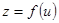 ,
,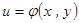 则
则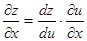 ,
,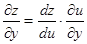
3、隐函数求偏导数的求法
1)一个方程的情况
设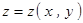 是由方程
是由方程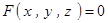 唯一确定的隐函数,则
唯一确定的隐函数,则
 ,
, 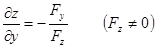
或者视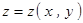 ,由方程
,由方程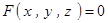 两边同时对
两边同时对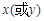 求导解出
求导解出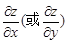 .
.
2)方程组的情况
由方程组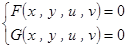 两边同时对
两边同时对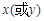 求导解出
求导解出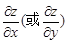 即可.
即可.
二、全微分的求法
方法1:利用公式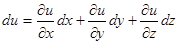
方法2:直接两边同时求微分,解出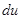 即可.其中要注意应用微分形式的不变性:
即可.其中要注意应用微分形式的不变性:

三、空间曲线的切线及空间曲面的法平面的求法
1)设空间曲线Г的参数方程为  ,则当
,则当 时,在曲线上对应点
时,在曲线上对应点 处的切线方向向量为
处的切线方向向量为 ,切线方程为
,切线方程为

法平面方程为 
2)若曲面 的方程为
的方程为 ,则在点
,则在点 处的法向量
处的法向量 ,切平面方程为
,切平面方程为

法线方程为 
若曲面 的方程为
的方程为 ,则在点
,则在点 处的法向量
处的法向量 ,切平面方程为
,切平面方程为

法线方程为 
四、多元函数极值(最值)的求法
1 无条件极值的求法
设函数 在点
在点 的某邻域内具有二阶连续偏导数,由
的某邻域内具有二阶连续偏导数,由 ,
, ,解出驻点
,解出驻点 ,记
,记 ,
, ,
, .
.
1)若 ,则
,则 在点
在点 处取得极值,且当
处取得极值,且当 时有极大值,当
时有极大值,当 时有极小值.
时有极小值.
2) 若 ,则
,则 在点
在点 处无极值.
处无极值.
3) 若 ,不能判定
,不能判定 在点
在点 处是否取得极值.
处是否取得极值.
2 条件极值的求法
函数 在满足条件
在满足条件 下极值的方法如下:
下极值的方法如下:
1)化为无条件极值:若能从条件 解出
解出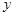 代入
代入 中,则使函数
中,则使函数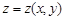 成为一元函数无条件的极值问题.
成为一元函数无条件的极值问题.
2)拉格朗日乘数法
作辅助函数 ,其中
,其中 为参数,解方程组
为参数,解方程组

求出驻点坐标 ,则驻点
,则驻点 可能是条件极值点.
可能是条件极值点.
3 最大值与最小值的求法
若多元函数在闭区域上连续,求出函数在区域内部的驻点,计算出在这些点处的函数值,并与区域的边界上的最大(最小)值比较,最大(最小)者,就是最大(最小)值.
主要:
1、偏导数的求法与全微分的求法;
2、空间曲线的切线及空间曲面的法平面的求法
3、最大值与最小值的求法
三、多元函数积分学复习要点
七种积分的概念、计算方法及应用如下表所示:


*定积分的几何应用
定积分应用的常用公式:
(1)面积 (
( 型区域的面积)
型区域的面积)
 (
( 型区域的面积)
型区域的面积)
(2)体积
 (横截面面积已知的立体体积)
(横截面面积已知的立体体积)
 (
( 所围图形绕
所围图形绕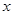 轴旋转所得的立体体积)
轴旋转所得的立体体积)
 (
( 所围图形绕
所围图形绕 轴旋转的立体体积)
轴旋转的立体体积)
 (
( 所围图形绕轴
所围图形绕轴 旋转的立体体积)
旋转的立体体积)
(3)弧长 
计算时注意:(1)正确选择恰当的公式;(2)正确的给出积分上下限;(3)注意对称性使问题简化;(4)注意选择恰当的积分变量以使问题简化.
计算多元函数的积分时要注意利用对称性简化积分的计算:
1)、对二、三重及第一类的线面积分,若积分区域关于变量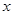 对称,则当被积函数关于
对称,则当被积函数关于 为奇函数时,该积分为0,当被积函数关于变量
为奇函数时,该积分为0,当被积函数关于变量 为偶函数时,则该积分为相应一半区域积分的二倍.
为偶函数时,则该积分为相应一半区域积分的二倍.
2)、对第二类的线面积分,关于积分变量的对称性理论与上相同,关于非积分变量
的对称性理论与上相反.
3)、若积分区域 的地位平等(即将表示区域的方程
的地位平等(即将表示区域的方程 互换不变),则将被积函
互换不变),则将被积函
数中 互换积分不变.此称之为轮换对称性.
互换积分不变.此称之为轮换对称性.
主要
1、交换二次积分的积分次序;
2、化三重积分为球面坐标或柱面坐标下的三次积分;
3、 公式计算法;
公式计算法;
4、Gaus公式计算法;
5、两曲面所围体积与旋转体的体积计算.
6.平面图形面积的计算。
所以:
第二篇:高数下册公式总结
第八章 向量与解析几何

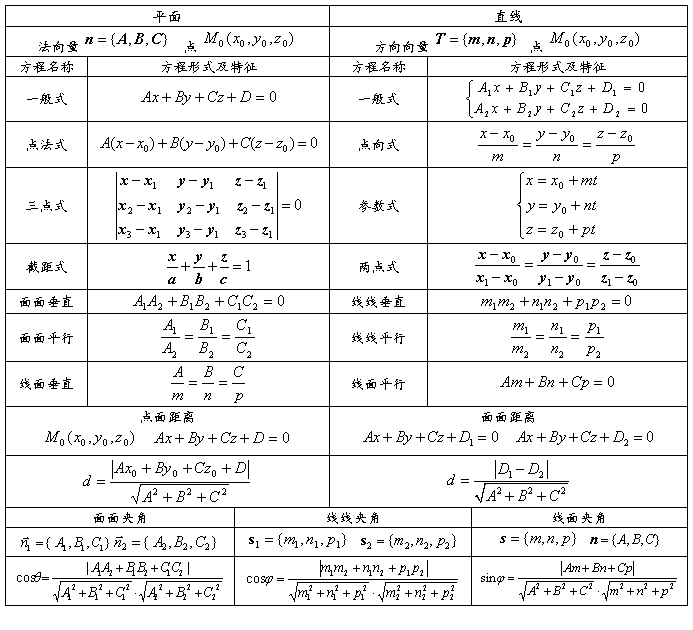

第十章 重积分
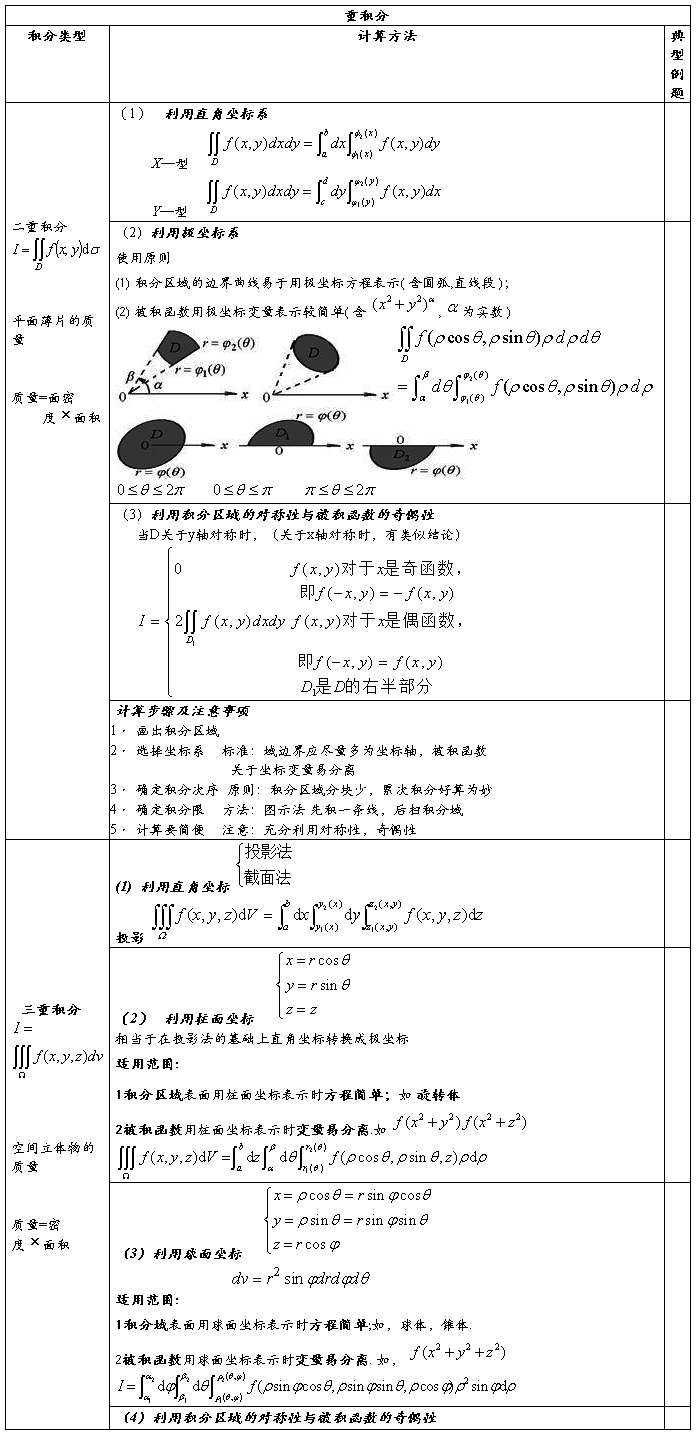
第十一章曲线积分与曲面积分

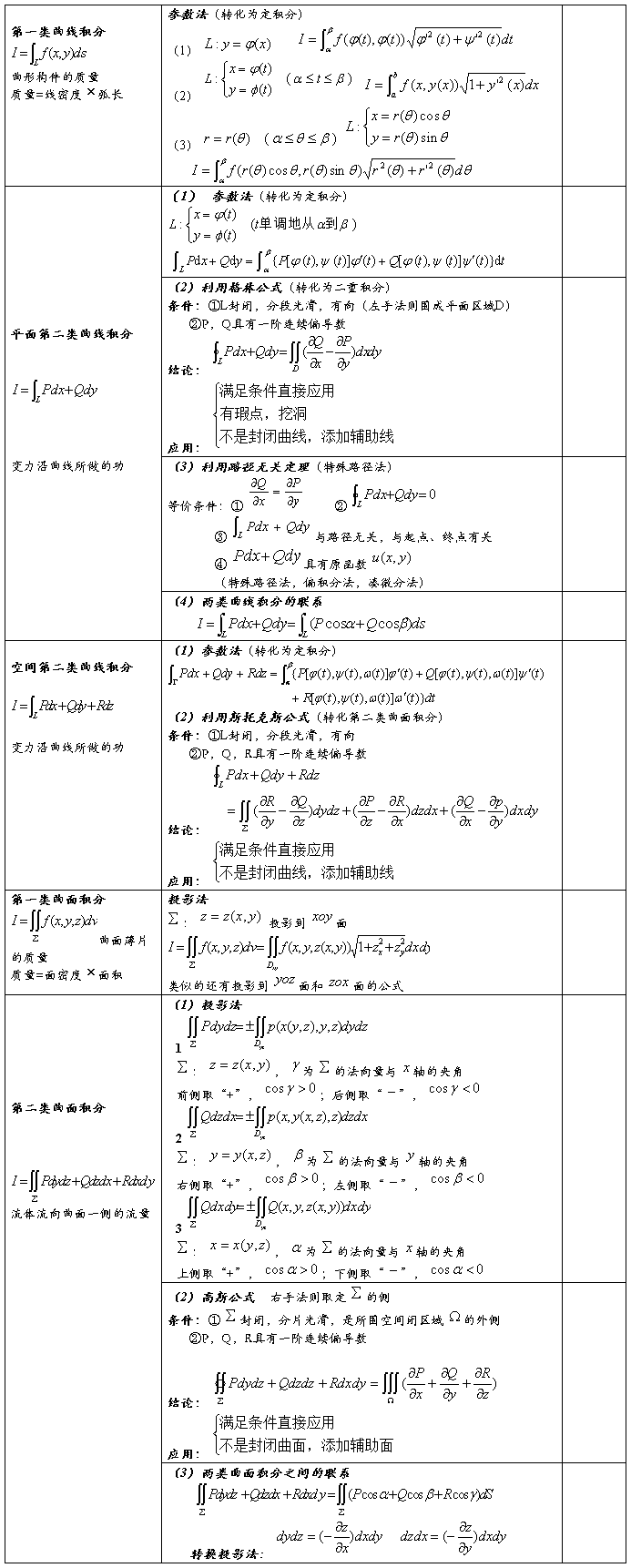
所有类型的积分:
1定义:四步法——分割、代替、求和、取极限;
2性质:对积分的范围具有可加性,具有线性性;
3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十二章 级数


-
高数下公式总结
高等数学下册公式总结1、N维空间中两点之间的距离公式:p(x1,x2,...,xn),Q(y1,y2,...,yn)的距离PQ?2…
-
高数总结
高等数学复习教程第一讲函数连续与极限一理论要求1函数概念与性质2极限3连续二题型与解法A极限的求法函数的基本性质单调有界奇偶周期几…
-
高数总结
高等数学复习教程第一讲函数连续与极限一理论要求1函数概念与性质2极限3连续二题型与解法A极限的求法函数的基本性质单调有界奇偶周期几…
-
高数下册总结
高数下小结一微分方程复习要点解微分方程时先要判断一下方程是属于什么类型然后按所属类型的相应解法求出其通解一阶微分方程的解法小结二阶…
-
高数下册总结(同济第六版)
高数同济版下高数下小结一微分方程复习要点解微分方程时先要判断一下方程是属于什么类型然后按所属类型的相应解法求出其通解一阶微分方程的…
-
小学数学一年级下册教学工作总结
一年级下册数学教学工作总结这一学期我担任一年级的数学课,本班学生绝大部分上课能够专心听讲,积极思考并回答老师提出的问题,下课能够按…
-
高数下册复习知识点总结
高数下册复习知识点总结:§8空间解析几乎与向量代数1.给定向量的坐标表达式,如何表示单位向量、方向数与方向余弦、投影。2.向量的数…
-
高数下册积分方法总结
积分方法大盘点现把我们学了的积分方法做个大总结1二重积分11X型区域上二重积分必须的基本方法1后x先y积分D往x轴上的投影得区间a…
-
大一高数(下)2,大一下学期高数总结归纳
河北科技大学高等数学下期末考试2一填空题共12分13分若a132b514则ab23分曲面x2y2z214在点123处的法线方程为3…
-
高等数学下册公式总结 (5页)
高等数学下册公式总结1N维空间中两点之间的距离公式px1x2xnQy1y2yn的距离PQ2多元函数zfxy求偏导时对谁求偏导就意味…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…