高中数列知识点总结                    

1.   等差数列的定义与性质 

定义：（为常数），

等差中项：成等差数列   前项和

性质：是等差数列

（1）若，则

（2）数列仍为等差数列，仍为等差数列，公差为；（3）若三个成等差数列，可设为

（4）若是等差数列，且前项和分别为，则

（5）为等差数列（为常数，是关于的常数项为0的二次函数）

的最值可求二次函数的最值；或者求出中的正、负分界项，

即：当，解不等式组可得达到最大值时的值.

当，由可得达到最小值时的值.  

 (6)项数为偶数的等差数列，有

，.   

（7）项数为奇数的等差数列，有

，，.

2. 等比数列的定义与性质

定义：（为常数，），.

等比中项：成等比数列，或.   前项和：

性质：是等比数列（1）若，则

（2）仍为等比数列,公比为.

注意：由求时应注意什么？时，；时，.

3．求数列通项公式的常用方法 （1）求差（商）法

如：数列，，求

解时，，∴                                        ①

时，                            ②

①—②得：，∴，∴

［练习］数列满足，求

注意到，代入得 又，∴是等比数列，

时，

（2）叠乘法

 如：数列中，，求

解，∴又，∴.

（3）等差型递推公式

由，求，用迭加法

时，两边相加得

∴

［练习］数列中，，求（）

（4）等比型递推公式

（为常数，）

可转化为等比数列，设

令，∴，∴是首项为为公比的等比数列

∴，∴

（5）倒数法

如：，求

由已知得：，∴

∴为等差数列，，公差为，∴，

∴

(公式法、利用、累加法、累乘法.构造等差或等比或、待定系数法、对数变换法、迭代法、数学归纳法、换元法)

4. 求数列前n项和的常用方法

(1) 裂项法

把数列各项拆成两项或多项之和，使之出现成对互为相反数的项.

如：是公差为的等差数列，求

解：由

∴

［练习］求和：

（2）错位相减法

若为等差数列，为等比数列，求数列（差比数列）前项和，可由，求，其中为的公比.

如：                                                      ①

                             ②

①—②

时，，时，

（3）倒序相加法

把数列的各项顺序倒写，再与原来顺序的数列相加.

相加

［练习］已知，则

     

由

∴原式

                                                

 

第二篇：高中数学数列知识点总结与题库

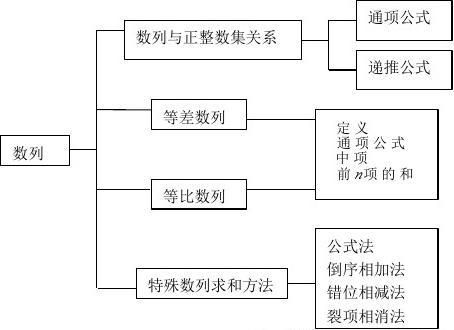
第六章

二、重难点击数列

本章重点：数列的概念，等差数列，等比数列的定义，通项公式和前n项和公式及运用，等差数列、等比数列的有关性质。注重提炼一些重要的思想和方法，如：观察法、累加法、累乘法、待定系数法、倒序相加求和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。

知识网络

四、数列通项an与前n项和Sn的关系

n

1．Sn=a1+a2+a3+?+an=∑ai

i=1

2．a?S1n=1

n=??Sn?Sn?1n≥2

课前热身

3．数列{an}的通项公式为an=3n2?28n,则数列各项中最小项是(B)

A．第４项B．第５项C．第６项D．第７项

4．已知数列{aa2

n}是递增数列，其通项公式为n=n+λn,则实数λ的取值范围是(?3,+∞)

5．数列{an}的前n项和Sn=n2?4n+1,，则a??2n=1

n=??2n?5n≥2

1

题型一归纳、猜想法求数列通项

【例1】根据下列数列的前几项，分别写出它们的一个通项公式

⑴7，77，777，7777，…

⑶1，3，3，5，5，7，7，9，9…解析：⑴将数列变形为7777×(10?1),(102?1),(103?1)，?,(10n?1)9999

⑶将已知数列变为1+0，2+1，3+0，4+1，5+0，6+1，7+0，8+1，9+0，…。可得数列的通项公式为

1+(?1)n

an=n+2

点拨：本例的求解关键是通过分析、比较、联想、归纳、转换获得项与项数的一般规律，从而求得通项。题型二应用a?S1(n=1)

n=??Sn?Sn?1(n≥2)求数列通项

例2．已知数列{an}的前n项和Sn，分别求其通项公式.

⑴Sn=3n?2

解析：⑴当n=1时,a1=S1=31?2=1，

当n≥2时,ann?1

n=Sn?Sn?1=(3?2)?(3?2)

=2?3n?1

又a?1(n=1)

1=1不适合上式，故an=??2?3n?1(n≥2)

三、利用递推关系求数列的通项

【例3】根据下列各个数列{an}的首项和递推关系，求其通项公式⑴a1

1=2,an+1=an+1

4n2?1

解析：⑴因为a1

n+1=an+4n2?1，所以

a=1111

n+1?an4n2?1=2(2n?1?2n+1所以aa111

2?1=2(1?3)

a=111

3?a22(3?5a?a111

43=2(5?7)

2

…，…，

111an?an?1=(?)22n?32n?1

以上(n?1)个式相加得

11(1?)22n?1

14n?3即：an=1?=4n?24n?2an?a1=

点拨：在递推关系中若an+1=an+f(n),求an用累加法，若an+1=f(n),求an用累乘法，若anan+1=pan+q，求an用待定系数法或迭代法。课外练习

3设an=111?++?+，(n∈N)，则an+1与an的大小关系是(C)n+1n+22n+1

B．an+1=A．an+1>an

C．an+1<

解：因为ananD．不能确定111+?2n+22n+3n+1

11=?<02n+32n+2an+1?an=

所以an+1<

二、填空题an，选Ｃ．

??2,(n=1)则an=?n2?4n+1，?2n?5,(n≥2)5．已知数列{an}的前n项和Sn=

7．已知数列{an}的通项n?98（n∈N?），则数列{an}的前30项中最大项和最小项分别是a10，a9n?99

解：构造函数y=x??=1+x?99x?99由函数性质可知，函数在(?∞99)上递减，且y<1函数在(99，＋∞）上递增且y>1

3

又∈(9，10）

∴a10>a11>a12>?>a30>1>a1>a2>?三、解答题

>a9

∴a10最大，a9最小

6.2等差数列

知识要点

2．递推关系与通项公式

递推关系：an+1?an=d通项公式：an=a1+(n?1)d推广：an=am+(n?m)d变式：a1=an?(n?1)d;

d=an?a1

n?1d=an

?amn?m

特征：an=dn+(a1?d),

即：an=f(n)=kn+m,(k,m为常数）

an=kn+m，（k,m为常数)是数列{an}成

等差数列的充要条件。３．等差中项：

若a,b,c成等差数列，则b称a与c的等差中项，且b=

a+c

2

；a,b,c成等差数列是2b=a+c的充要条件。４．前n项和公式

S(a1

+an)nn(n=2；Snan?1)d

n=1+2

特征：Sdn=

2n2+(ad

1?2)n,即S2n=f(n)=An+BnS2

n=An+Bn

(A,B为常数)

是数列{an}成等差数列的充要条件。

5．等差数列{an}的基本性质(其中m,n,p,q∈N?

)

⑴若m+n=

p+q，则am+an=ap+aq反

之，不成立。

⑵an?am=(n?m)d⑶2an=

an?m+an+m

⑷Sn,S2n?Sn,S3n?S2n仍成等差数列。６．判断或证明一个数列是等差数列的方法：

①定义法：

an+1?an=d(常数）（n∈N?）?{an}是等

差数列

②中项法：

2an+1=an+an+2

（n∈N?)?{an}是等差数

列

③通项公式法：

an=kn+b

(k,b为常数)?{an}是等差数

列

④前n项和公式法：

Sn=An2+Bn

(A,B为常数)?{an}是等

差数列课前热身

2．等差数列{an}中，

a4+a6+a8+a10+a12=120,

则a1

9?3

a11的值为(C)

A．14

B．15

C．16

D．17

解a13a1

9?11=a9?3(a9+2d)

=23(a?d)=2212093a8=3?5

=164

。

3．等差数列{an}中，a1>0，S9=S12，则前或11项的和最大。解：∵S9=

S12，S12?S9=0

∴a10+a11+a12=0，∴3a11=0，∴a11=0，又a1>0

∴{an}为递减等差数列∴S10=

S11为最大。

4．已知等差数列{an}的前10项和为100，前100项和为10，则前110项和为－110解：∵

S10，S20?S10，S30?S20，?，S110?S100，?

成等差数列，公差为D其首项为

S10=100，前10项的和为S100=10∴100×10+10×9

2

×D=10，∴D=?22又S110

?S100=S10+10D

∴S110=100+10+10（??22）=?110

y=50n?98??

n??12n+(n?1)?2×4?

?

=?2n2+40n?98=?2(n?10)2+102所以当n=10时，ymax=102

６．设等差数列{an}的前n项和为Sn，已知

a3=12，S12>0，S13<0

①求出公差d的范围，

②指出S1，S2，?，S12中哪一个值最大，并说明理由。

dan=f(n)nanSn{an}"n≥2"

解：①S12=6(a1+a12)=6(a3+a10)

=6(2a3+7d)>0

∴24+7d>0∴d>?

247

又S13(a1+a13)13=

2=13

2(a3+a11)=13

2

(2a3+8d)<0∴24+8d<0∴d<?3

从而?24

7

<d<?3

②

∵S12=6(a6+a7)>0

S13=13a7<0∴a7<0，a6>0

∴S6最大。

课外练习一、选择题

1．已知{an}数列是等差数列，a10=10，其前10

项的和S10=70，则其公差d等于(D)

A．?23

B．?

13C13

D23

2．已知等差数列

{an}

中，

a7+a9==16，a4=1，则a12等于（A）

A．15

B．30

C．31

D．64

解：∵a7+a9=a4+a12

∴a12=15

二、填空题3．设

Sn为等差数列{an}的前n项和，

S4=14，S10?S7=30，则S9=54

4．已知等差数列

{an}的前n项和为Sn，若

S12=21，则a2+a5+a8+a11=

5

5．设F是椭圆x2y2

7+6

=1的右焦点，且椭圆上至

少有21个不同点

Pi(i=1,2,?)使P1FP2FP3F,?

组成公差为

d的等差数列，则d的取值范围为

????110，0???∪???01?10?

解：椭圆的焦点F到椭圆上的点最大、最小距离分别为(+1)?1），由题意得：

7?1）+（n?1)d=7+1∴d=

2

n?1∵n?1≥20

∴d≤1

10d≠0

∴?110≤d<0或0<d≤

110三、解答题6．等差数列

{an}的前n项和记为Sn，已知

a10=30，a20=50

①求通项an；②若Sn=242，求n解：an=a1+(n?1)d

a10=30，a20=50解方程组??a1

+9d=30

?a1+19d=50

∴??a1=12?d=2

∴an=2n+10由Sn=

na1+

n(n?1)d

2

，Sn=242∴12n+

n(n?1)

2

?2=242解得n=11或n=?22(舍去）

7．甲、乙两物体分别从相距70m的两处同时相向运

动，甲第一分钟走2m，以后每分钟比前一分钟多

走1m，乙每分钟走5m，①甲、乙开始运动后几分钟相遇？②如果甲乙到对方起点后立即折返，甲继续每分钟比前一分钟多走1m，乙继续每分钟走5m，那么，开始运动几分钟后第二次相遇？解：①设n分钟后第一次相遇，依题意有：

2n+

n(n?1)

2

+5n=70解得n=7，n=?20(舍去）故第一次相遇是在开始运动后7分钟。②设n分钟后第二次相遇，则：

2n+

n(n?1)

2

+5n=3×70解得n=15，n=?28(舍去）故第二次相遇是在开始运动后15分钟10．已知数列

{an}

中，

a1=3，前n和

Sn=

1

2

(n+1)(an+1)?1①求证：数列{an}是等差数列②求数列{an}的通项公式

③设数列?

1?

a?的前n项和为Tn，是否存在实

?nan+1?

数M，使得Tn≤

M对一切正整数n都成立？若存

在，求M的最小值，若不存在，试说明理由。解：①∵Sn=

1

2

(n+1)(an+1)?1∴S1

n+1=2

(n+2)(an+1+1)?1∴an+1=Sn+1?Sn

=

1

2

[(n+2)(an+1+1)?(n+1)(an+1)]整理得，nan+1=(n+1)an?1

∴(n+1)an+2=(n+2)an+1?1∴(n+1)an+2?nan+1=(n+2)an+1?(n+1)an∴2(n+1)an+1=(n+1)(an+2+an)∴2an+1=an+2+an

∴数列{an}为等差数列。

6

②a1=3，nan+1=(n+1)an?1

∴a2=2a1?1=5∴a2?a1=2

即等差数列{an}的公差为2∴an=a1+(n?1)d=3+(n?1)?2=2n+1

③∵

11

=

anan+1(2n+1)(2n+3)

1?11?

???

2?2n+12n+3?

1111111

∴Tn=(?+?+?+?235572n+12n+3111=(?232n+3

1

又当n∈N?时，Tn<

6=

要使得Tn≤

M对一切正整数n恒成立，只要M≥

1

，所以存在实数M使得Tn≤M对一切正整数n6

都成立，M的最小值为

1。6

6.3等比数列

知识要点

1．定义：如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，记为

①若m+n=p+q，则am?an=ap?aq反之不真！

②q

n?m

q，（q≠0)。

2．递推关系与通项公式

=

an2

，an=an?m?an+m(n∈N?)am

递推关系：an+1=qan通项公式：an=a1?qn?1推广：an=am?qn?m

3．等比中项：若三个数a,b,c成等比数列，则称b为

③{an}为等比数列，则下标成等差数列的对应项成等比数列。

④

q≠?1时，Sn，S2n?Sn，S3n?S2n，?仍

成等比数列。

6．等比数列与等比数列的转化①{an}是等差数列?等比数列；②

a与c的等比中项，且为b=±ac，注：b2=ac

是成等比数列的必要而不充分条件。4．前n项和公式

{c}

an

(c>0，c≠1)是

(q=1)?na1

?n

Sn=?a1(1?q)a1?anq

=

?1?q?1?q

{an}

是正项等比数列

(q≠1)

?{logcan}

(c>0，c≠1)是等差数列；

③{an}既是等差数列又是等比数列?

?

{an}是各

7

5．等比数列的基本性质，(其中m,n,p,q∈N)

项不为零的常数列。

7．等比数列的判定法①定义法：

an+1

a=q（常数）?{an}为等比数列；n

②中项法：a2

n+1=an?an+2

(an≠0)?{an}为

等比数列；

③通项公式法：an=

k?qn(k,q为常数）?{an}

为等比数列；④前

n项和法：

Sn=k(1?qn)（k,q为常数）?{an}为等比数

列。

1．设f(n)=2+24+27+2

10

+?+23n+10

(n∈N?)，则f(n)等于（D）A2(8n?1)B2(8n+177?1)C27(8n+3?1)D27

(8n+4?1)2．已知数列

{an}

是等比数列，且

Sm=10，S2m=30，则S3m=猜想：{b1

n}是等比数列，公比为2。证明如下：∵bn+1

=a111

2n+1?4=2a2n?

4

=

12(a+11

2n?14)?4=12(a112n?1?4=2bn

即：

bn+1b=12，∴{b1

n}是首项为a?4

，公比n为1

2

的等比数列。二、性质运用例

2：⑴在等比数列

{an}

中，

a1+a6=33，a3a4=32，an>an+1

①求an，

②若Tn=lga1+lga2+?+lgan,求Tn⑵在等比数列{an}中，若a15=0，则有等式

a1+a2+?+an=a1+a2+?+a29?n

(n<29，n∈N?)成立，类比上述性质，相应的

在等比数列{bn}中，若b19=1则有等式立。

解：⑴①由等比数列的性质可知：

a1?a6=a3?a4=32

又a1+a6=33，a1>a6

解得a1=32，a6=1

所以a6a=132，即q5=1132，∴q=

12所以a?(1

n=32)n?1=26?n

2

②由等比数列的性质可知，{lgan}是等差数列，因为

lgan=lg26?n=(6?n)lg2，lga1=5lg2所以Ta1+lgan)nn=

(lg2=n(11?n)

2

lg2

⑵由题设可知，如果

am=0在等差数列中有

a1+a2+?+an=a1+a2+?+a2m?1?n

(n<2m?1，n∈N?)成立，我们知道，如果

若m+n=p+q，则am+an=ap+aq，而对于

等

比

数

列

{bn}

，则有

若m+n=p+q，则am?an=ap?aq所以可以得

出结论，若

bm=1，则有b1b2?bn=b1b2?b2m?1?n

(n<2m?1，n∈N?)成立，在本题中

8

则有b1b2?bn=b1b2?b37?n(n<37，n∈N?)

点拨：历年高考对性质考查较多，主要是利用“等积性”，题目“小而巧”且背景不断更新，要熟练掌握。典例精析

一、错位相减法求和例1：求和：S1n=a+23n

a2+a3+?+a

n解：⑴

a=1时，S+3?+n=

n(n+1)

n=1+22

⑵a≠1时，因为a≠0

Sn=

1a+23na2+a3+?+an①112aSn?1nn=a2+a3+?+an+a

n+1②

由①－②得：

(1?1a)S=111nna+a2+?+an?a

n+1

11a(1?=n?n1?1an+1a

所以Sa(an?1)?n(a?1)

n=

an(a?1)2综上所述，

?n?(n+1)?2(a=1)

Sn=??a(an

?1)?n(a?1)??

an(a?1)2a≠1)

点拨：①若数列{an}是等差数列，{bn}是等比数列，

则求数列{an?bn}的前n项和时，可采用错位相减法；

②当等比数列公比为字母时，应对字母是否为1进行讨论；③当将Sn与q

Sn相减合并同类项时，注意错

位及未合并项的正负号。二、裂项相消法求和

例2：数列

{an}

满足

a1

=8，

a4=2，且an+2?2an+1+an=0（n∈N?）

①求数列{an}的通项公式；则d

=

a4?a1

4?1

=?2所以，an=8＋（n－1）×（－2）＝―10－2n

b11

n=n(14?a=

n)2n(n+2)

=

14(1n?1

n+2)所以

②Tn=b1+b2+?+bn

=

1?4??(11?13+(12?14)+?+(11?n?n+2??=14(1+1112?n+1?n+2=38?14(n+1)?1m4(n+2)>32对一切n∈N?恒成立。

∴m<12?

8n+1?8

n+2

对一切n∈N?恒成立。对n∈N?，（12?88

n+1?n+2)min=

12?8816故1+1?1+2=

3所以m<

16

3

m的最大整数值为5。

点拨：①若数列

{an}

的通项能转化为

f(n+1)?f(n)的形式，常采用裂项相消法求和。

②使用裂项消法求和时，要注意正负项相消时，消去了哪些项，保留了哪些项。三、奇偶分析法求和例3：设二次函数f(x)=

x2+x，当x∈[n，n+1]

9

1．在等差数列{an}中，a1=1，前n项和Sn满足

(1?p)Tn=p+p2+?+pn?npn+1

S2n4n+2

=n=1，2，?Snn+1

①求数列{an}的通项公式②记bn=anpan

p(1?pn)

=?npn+1

1?p

p(1?pn)npn+1

所以Tn=?2

1?p(1?p)n(n+1)?

??2即：Tn=?n

p(1?p)npn+1??(p=1)(p≠1)

(p>0)，求数列{bn}的前n

项和Tn。

解：①设数列

{an}

的公差为

d，S2n4nS=+2

n+1n=1，2，?n得

a1+a2

a=3，所以a2=21

即d=a2?a1=1

又4n+2S2n

n+1=

Sn(an+nd+a1)2n

=

(an+a1)n

2

=

2(an+n+1)an+1

所以an=n②由ban=anpn

(p>0)，有bn

n=np所以T3n=

p+2p2+3p+?+npn

①

当p=1时，Tn(n+1)

n=

2当p≠1时，

pTn=p2+2p3+?+(n?1)pn+npn+1②

①－②得

??

(1?p)21?p课外练习

１．数列

{an}

的前

n项和为Sn，若

a1

n=

n(n+1)

，则S5等于（B）

A．1B．

516

C．

6D．1

30

解：因为a=111

nn(n+1)=n?

n+1所以S111111

5=(1?2)+(2?3+?+(5?6)

=56

４．

f(x)的定义域为R，且f(x)是以2为周期的

周期函数，数列{an}是首项为a(a∈N?)，公差为1的等差数列，那么f(a1)+f(a2)+?+f(a10)的

值为（C）

A．－1

B．1

C．0

D．10a

解：因为函数f(x)的定义域为R，且f(x)是以2为周期的周期函数，所以

f(0）=0，且f(x+2)=f(x)

又数列{an}是首项为a，公差为1的等差数列

10

由

所以an=a+n?1，又a∈N?f(a?f(a)（n为奇数）

n)=?

?f(a+1)（n为偶数）

所以f(a1)+f(a2)+?+f(a10)

=5f(a)+5f(a+1)=5[f(0)+f(1)]=5f(1)又f(?1)f(?1+2)=f(1)所以?f(1)=f(1)

即f(1)=0

故原式=0，选C。二、填空题

５．设等比数列{an}的公比与前n项和分别为q和

Sn，且q≠1，S10=8，则

S20

1+q

10

=8

a1(1?q10)

1?2=8

S20a1(1?q20∴1+q10=)(1+q10）(1?q)

=8方法二、S20=S10+a11+a12+?+a20

=S1010+qS10=S10(1+q10)所以

S20

1+q10

=S10=8

6．数列{an}满足an=

12nn+1+n+2+?+n+1

又b=

2n，则数列

a{bn}的前n项和为

8nnan+1

解：a1n=

n+1(1+2+?+n)=n2b28n=a=11nan+1n(n+1)=8(n?n+1

）所以b1+b2+?+b=8?11

1n

111??(1?2+(2?3)+?+(n??n+1?

=8?

1?

??1??8nn+1??=n+1

７．数列11xxxxxxxxxxxx4444

，?的前100项的和为13

914

。（n∈N?

）11

典例精析

一、函数与数列的综合问题

例1：已知f(x)=logax(a>0且a≠1)，

设f(a1)，f(a2)，?，f(an)(n∈N?)

是首项为4，公差为2的等差数列。

①设a是常数，求证：{an}成等差数列；

②若bn=anf(an)，{bn}的前n项和是Sn，当a=2时，求Sn

解：①f(an)=4+(n?1)×2=2n+2，

即logaan=2n+2，所以an=a2n+2

ana2n+2

所以=2n=a2(n≥2)为定值an?1a

所以{an}为等比数列。

②bn=anf(an)

=a2n+2logaa2n+2=(2n+2)a2n+2

当a=2时，

bn=(2n+2)?()2n+2=(n+1)?2n+2

Sn=2?23+3?24+4?25+?+(n+1)?2n+2

2Sn=2?24+3?25+?+n?2n+2+(n+1)?2n+3点拨：本例是数列与函数综合的基本题型之一，特两式相减得

?Sn=2?23+24+25+?+2n+2?(n+1)?2n+3

24(1?2n?1)=16+?(n+1)?2n+3

1?2

所以Sn=n?2n+3

征是以函数为载体构建数列的递推关系，通过由函数的解析式获知数列的通项公式，从而问题得到求解。１．已知正项数列{an}的前n项和为Sn，

①求证：数列{an}是等差数列；②若bn=1Sn是与(an+1)2的等比中项，4an，数列{bn}的前n项和为Tn，求Tn2n

?Tn+λ?为等比数列？若存在，试求出λ；若不存在，说明理由。a?n+2?③在②的条件下，是否存在常数λ，使得数列?

解：①1Sn是与(an+1)2的等比中项，4

12

1(an+1)2

4

1当n=1时，a1=(a1+1)2，∴a1=14

1当n≥2时，Sn?1=(an?1+1)2

4

所以an=Sn?Sn?1所以Sn=

122(an?an?1+2an?2an?1)4

即(an+an?1)(an?an?1?2)=0=

因为an>0，所以an?an?1?2=0

即：an?an?1=2

所以数列{an}是等差数列。②Tn=3?2n+3

2n

Tn+λ2n+31=(3?+λ)×an+22n2n+3

=3+λ1?n2n+32

?Tn+λ??为等比数列。

?an+2?所以当且仅当3+λ=0，即λ=－3时，数列

２．已知在正项数列{an}中，a1=2，且

22在双曲线y?x=1上，An(anan+1）

数列{bn}中，

点（bn，Tn）在直线1y=?x+1上，其中Tn是数列{bn}的前n项和，①求数列{an}的通项公式；②求证：数列{bn}是2

等比数列。③若Cn=an?bn，求证：Cn+1<Cn。解：①由已知带点An(在y2?x2=1上知，anan+1）

an+1－an＝１，所以数列{an}是以2为首项，以1为公差的等差数列。

所以an=a1+(n?1)d=n+1

②因为点（bn,Tn）在直线y=?1x+1上，2

13

1所以Tn=?bn+121所以Tn?1=?bn?1+12两式相减得：

11bn=Tn?Tn?1=?bn+bn?122

1所以bn=bn?1，312令n=1得b1=?b1+1，所以b1=232所以{bn}是一个以为首项，31以为公比的等比数列。3212所以bn=?(n?1=n333

③Cn=an?bn=(n+1)?2

3n

2

3n+1?(n+1)23n所以Cn+1?Cn=(n+2)?

=2?(?2n?1)<03n+1

所以Cn+1<Cn

一、选择题

2n{a}a>0,n=1,2,?a?a=2(n≥3)，则当n≥1时，nn52n?51.（2009广东卷理）已知等比数列满足，且

log2a1+log2a3+?+log2a2n?1=

A.n(2n?1)2B.(n+1)2C.n2D.(n?1)

22nna?a2n?5=22n(n≥3)a=2a>0a=25nnn【解析】由得，，则，log2a1+log2a3+???+

log2a2n?1=1+3+???+(2n?1)=n2

，选C.

答案C

2.（2009辽宁卷理）设等比数列{an}的前n项和为Sn，若S6S3=3，则S9S6=

A.2B.73C.83D.3

S6(1+q3)S3=SS3【解析】设公比为q,则3＝1＋q3＝3?q3＝2

14

于是

【答案】B

S91+q3+q61+2+47===S61+q31+23

?an

?,当an为偶数时，an+1=?2

?a＝m{a}a＝1，则m所有?3an+1,当an为奇数时。14.(2009湖北卷理)已知数列n满足：1（m为正整数），若6

可能的取值为__________。

答案4532

a解析（1）若a1aa1=m为偶数，则2为偶,故2=m

2 a2m3=2=4mamm

m

4=8??????a6=

32=1?m=32①当4仍为偶数时，

故

323

mm+1

②当4a=3a=3为奇数时，43+14m+1??????a6=43

m+1故4=1得m=4。

am+1

（2）若

a1=m为奇数，则a2=3a1+1=3m+1为偶数，故3=

32必为偶数

??????a3m+13m+1

6=

16，所以16=1可得m=5

16.（2009陕西卷文）设等差数列{an}的前n项和为sn,若a6=s3=12,则an=

解析:由a6=s3=12可得{an}的公差d=2,首项a1=2,故易得an=2n.

答案:2n

{lim

S17.(2009陕西卷理)设等差数列a}的前n项和为Sn,若a6=Sn

n3=12,则

n→∞n2=解析：??a6=12?a1+5d=12?a1=2Snn+1?s3=12???a1

+d=12???d=2?Sn=n(n+1)?n2=n?limSnn→∞n2=limn+1

n→∞n=1答案：1

a=1,a=1n+1

22.（2009全国卷Ⅰ理）在数列{an}中，

1n+1(1+n)an+2n.

.

15

ban

（I）设n=n，求数列{bn}的通项公式

（II）求数列{an}的前n项和Sn

an+1=an+11

分析：（I）由已知有n+1n2n∴bn+1?bn=2n

{bb

利用累差迭加即可求出数列n}的通项公式:n=2?1

2n?1(n∈N*)

a2n?n

（II）由（I）知n=2n?1,

n

∴Sn=∑(2k?knn=k=12∑(2k)?

k=1∑kk?1kk?1=12

nn

n(n+1)

而∑(2k)=k=1,又∑kk=12k?1是一个典型的错位相减法模型，∑nk

kk?1=4?n+2易得=122n?1∴S+n+2?4

n=n(n+1)2n?1

23.（2009北京理）已知数集A={a1,a2,?an}(1≤a1<a2<?an,n≥2)具有性质P；对任意的

aj

i,j(1≤i≤j≤n)，aiaj与ai两数中至少有一个属于A.

（Ⅰ）分别判断数集{1,3,4}与{1,2,3,6}是否具有性质P，并说明理由；

a1+a2+?+an=an

（Ⅱ）证明：a1=1?1+a?1?1

，且a12+?+an；

（Ⅲ）证明：当n=5时，a1,a2,a3,a4,a5成等比数列.

【解析】本题主要考查集合、等比数列的性质，考查运算能力、推理论证能力、分

分类讨论等数学思想方法．本题是数列与不等式的综合题，属于较难层次题.

4

（Ⅰ）由于3×4与3均不属于数集{1,3,4}，∴该数集不具有性质P.1×2,1×3,1×6,2×3,661236

由于2,3,1,2,3,6都属于数集{1,2,3,6}，

∴该数集具有性质P.

16

an

A={a1,a2,?an}aaa（Ⅱ）∵具有性质P，∴nn与n中至少有一个属于A，由于1≤a1<a2<?<an，∴anan>an，故anan?A.1=

从而

∵an∈Aa=1.an，∴11=a1<a2<?<an，∴akan>an，故akan?A(k=2,3,?,n).

an∈A(k=1,2,3,?,n)

由A具有性质P可知ak.anaaa<n<?<n<n

a2a1，又∵anan?1

anaaa=1,n=a2,?n=an?1,n=anan?1a2a1∴an，anaaa=n+?+n+n=a1+a2+?+an?1+anaan?1a2a1从而n，a1+a2+?+an=an?1?1?1a+a+?+a2n∴1.

a5a=a2,5=a32a=aa=aaan=5524343（Ⅲ）由（Ⅱ）知，当时，有，即，

∵1=a1<a2<?<a5，∴a3a4>a2a4=a5，∴a3a4?A，

a4∈A

由A具有性质P可知a3.

a3a4a3a4a3=∈A1<=a==a222a2a4=a3aa3a2aa2，得2，且，∴3，a5a4a3a2====a2a,a,a,a,aaaaaa321∴4，即12345是首项为1，公比为2成等比数列.

Tn表示关于x的一元二次方程x2+2ax+b=0有实数根的有序数组(a,b)的

a,b∈{1,2,?,n}（a和b可以相等），记25（2009江苏卷）对于正整数n≥2，用组数，其中a,b∈{1,2,?,n}（a和b可以相等）；对于随机选取的Pn为关于

x的一元二次方程x2+2ax+b=0有实数根的概率。

17

（1）求Tn2和Pn2；

（2）求证：对任意正整数n≥2

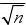
，有Pn>1.

【解析】[必做题]本小题主要考查概率的基本知识和记数原理，考查探究能力。满分10

分。

29.（2009江西卷理）各项均为正数的数列{an}，a1=a,a2=b，且对满足m+n=p+q的正整数m,n,p,q都有

ap+aqam+an=.(1+am)(1+an)(1+ap)(1+aq)

14a=,b=25时，求通项an;（1）当

1≤an≤λ.aanλ（2）证明：对任意，存在与有关的常数，使得对于每个正整数，都有λ

解：（1）由ap+aqam+an=(1+am)(1+an)(1+ap)(1+aq)得

a1+ana2+an?1=.a=1,a=4

(1+a1)(1+an)(1+a2)(1+an?1)将1225代入化简得

an=2an?1+1.an?1+2

1?an11?an?1=?,1+a31+ann?1所以

18

{1?an

故数列1+an为等比数列，从而

1?an

+a=1n

n,a=3?1

1.

n3即n3n+1

a3n?1

可验证，n=3n+1满足题设条件.

am+an

(2)由题设(1+am)(1+an)的值仅与m+n有关,记为bm+n,b=a1+ana+an

n+1

则(1+a=.

1)(1+an)(1+a)(1+an)

f(x)=a+x

(1+a)(1+x)(x>0)

考察函数,则在定义域上有

??1

1+a,a>1

?

f(x)≥g(a)=??1,a=1

?2

??a

?1+a,0<a<1

故对n∈N*，bn+1≥g(a)恒成立.bn

2n=2a

(1+a2≥g(a)

又n),0<g(a)≤1

注意到2,

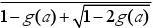
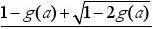
解上式得

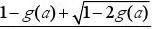
=≤an≤λ=1

取λ≤a≤λ.

,即有n.

30.(2009湖北卷理)已知数列{an}S1n的前n项和n=?an?(2)?1+2

（n为正整数）。

（Ⅰ）令bn=2nan，求证数列{bn}是等差数列，并求数列{an}的通项公式；

cn+1

na5n

(Ⅱ）令n=n，Tn=c1+c2+........+cn试比较Tn与2n+1的大小，并予以证明。

Sa11+21解（I）在n=?n?(2n?

中，令n=1，可得S1=?a=aa=

n?1+21，即12

19

n≥2Sa12+2，∴aa1

时，n?1=?n?1?()n?

n=Sn?Sn?1=?n+an?1+()n?1

当22，∴2a=a1?1

nn?1+(2n,即2nan=2n?1an?1+1

.

∵bn

n=2an,∴bn=bn?1+1,即当n≥2时，bn?bn?1=1.

又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列.bn=1+(n?1)?1=n=2nan,∴an=n

于是2n.

cn+1

(II)由（Ina1

）得n=n=(n+1)(2)n

，所以

T=2×1+3×(12+4×(11

n23+K+(n+1)(2)n

22

1

2T1111

n=2×(22+3×(23+4×(24+K+(n+1)(2)n+1

1T+(12+(13+K+(1n?(n+1)(1

n=1n+1

由①-②得22222

1[1?(1)n?1]

=1+?(n+1)(1)n+13n+3

1?12=2?2n+1

2

∴Tn+3

n=3?2n

T?5nn+35n(n+3)(2n?2n?1)

n2n+1=3?2n?2n+1=2n(2n+1)

T5n

于是确定n与2n+1的大小关系等价于比较2n与2n+1的大小由2<2×1+1;22<2×2+1;23<2×3+1;24<2×4+1;25<2×5;K可猜想当n≥3时，2n>2n+1.证明如下：

证法1：（1）当n=3时，由上验算显示成立。

（2）假设n=k+1时2k+1=2g2k>2(2k+1)=4k+2=2(k+1)+1+(2k?1)>2(k+1)+1所以当n=k+1时猜想也成立

综合（1）（2）可知，对一切n≥3的正整数，都有2n>2n+1.

20

证法2：当n≥3时

012n?1n01n?1n2n=(1+1)n=Cn+Cn+Cn+K+Cn+Cn≥Cn+Cn+Cn+Cn=2n+2>2n+1

综上所述，当n=1,2时Tn<5n5nTn>2n+1，当n≥3时2n+1

31.（2009四川卷文）设数列

（I）求数列{an}的前n项和为Sn，a=5Sn+1成立，对任意的正整数n，都有n记bn=4+an(n∈N*)1?an。{an}与数列{bn}的通项公式；

{bn}的前n项和为Rn，是否存在正整数k，使得Rn≥4k成立？若存在，找出一个正整数k；若不存在，

Tn<3

2；（II）设数列请说明理由；（III）记cn=b2n?b2n?1(n∈N)，设数列{cn}的前n项和为Tn，求证：对任意正整数n都有*

解（I）当n=1时，

又a1=5S1+1,∴a1=?14∵an=5Sn+1,an+1=5Sn+1+1

∴an+1?an=5an+1,即an+11=?an4

11q=?4，公比为4的等比数列，∴数列{an}是首项为a1=?

14+(?)n

(n∈N*)bn=11an=(?)n1?(?)n

4，4∴

（II）不存在正整数k，使得…………………………………3分Rn≥4k成立。

14+(?)n5=4+bn=n1n(?4)?11?(?)4证明：由（I）知

552015×16k?40∵b2k?1+b2k=8++=8+k?k=8?k<8.2k?12kk(?4)?1(?4)?116?116+4(16?1)(16+4)5

?n=2m(m∈N)∴当n为偶数时，设

21

∴Rn=(b1+b2)+(b3+b4)+?+(b2m?1+b2m)<8m=4n

当n为奇数时，设n=2m?1(m∈N?)

∴Rn=(b1+b2)+(b3+b4)+?+(b2m?3+b2m?2)+b2m?1<8(m?1)+4=8m?4=4n∴对于一切的正整数n，都有Rn<4k

∴不存在正整数k，使得Rn≥4k成立。…………………………………8分

b5

n=4+

（III）由(?4)n?1得

5515×16n15×16n

c15×16n15n=b2n?1+b2n=42n?1+42n?1+1=(16n?1)(16n+4)=(16n)2+3×16n?4<(16n)2=16nb13

1=3,b2=3,∴c4

2=3，

3

当n=1T

时，1<2，

当n≥2时，

1[1?1n?2

T411142(]

n<3+25×(162+163+?+16n=3+25×1?1

16

1

<42

3+25×693

1?=48<2

16

32.（2009湖南卷文）对于数列{un},若存在常数M＞0,对任意的n∈N*，恒有un+1?un+un?un?1+?+u2?u1≤M,则称数列{un}为B?数列.

?1

（Ⅰ）首项为1，公比为2的等比数列是否为B-数列？请说明理由;（Ⅱ）设Sn是数列{xn}的前n项和.给出下列两组判断：

A组：①数列{xn}是B-数列,②数列{xn}不是B-数列;

B组：③数列{Sn}是B-数列,④数列{Sn}不是B-数列.

请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题.又

22

判断所给命题的真假，并证明你的结论；

(Ⅲ)若数列{an}是B-数列，证明：数列{a2

n}也是B-数列。

1

解:（Ⅰ）设满足题设的等比数列为{aan?1

n},则n=(?2.于是

a?a11n?2=31

nn?1=(?)n?1?(?)2×(2)n?2

22,n≥2.

|an+1?an|+|an?an?1|+?+|a2?a1|

3×??1+1+（1）2+?+（1n-1?3×?1?（1）n?

=2?222??=??2??<3.

?1

所以首项为1，公比为2的等比数列是B-数列.（Ⅱ）命题1：若数列{xn}是B-数列，则数列{Sn}是B-数列.此命题为假命题.事实上设xn=1，n∈N*，易知数列{xn}是B-数列，但Sn=n，

|Sn+1?Sn|+|Sn?Sn?1|+?+|S2?S1|=n.

由n的任意性知，数列{Sn}不是B-数列。

命题2：若数列{Sn}是B-数列，则数列{xn}不是B-数列。此命题为真命题。事实上，因为数列{Sn}是B-数列，所以存在正数M，对任意的n∈N*，有

|Sn+1?Sn|+|Sn?Sn?1|+?+|S2?S1|≤M,

即|xn+1|+|xn|+?+|x2|≤M.于是xn+1?xn+xn?xn?1+?+x2?x1≤xn+1+2xn+2xn?1+?+2x2+x1≤2M+x1,

所以数列{xn}是B-数列。

（注：按题中要求组成其它命题解答时，仿上述解法）

(Ⅲ)若数列{an}是B-数列，则存在正数M，对任意的n∈N?,有an+1?an+an?an?1+?+a2?a1≤M.因为an=an?an?1+an?1+an?2+?+a2?a1+a1

≤an?an?1+an?1?an?2+?+a2?a1+a1≤M+a1.

23

记K=M+a1，则有22an?a+1n=(an+1+an)(an+1?an)

≤(an+1+an)an+1?an≤2Kan+1?an

因此..222222an+1?an+an?an?1+...+a2?a1≤2KM

2

n{a}是B-数列.故数列

x＝11x＝,n∈N*

33.(2009陕西卷理)已知数列{xn}1

满足，2’n＋11+xn.

(Ι)猜想数列{xn}的单调性，并证明你的结论；

|x12

（Ⅱ)证明：n+1-xn|≤(5n?1

6。

x=1及x12513

1n+1=得x2=+x4

证明（1）由21+x=，x4=

n3821

由x2>x4>x6猜想：数列{x2n}是递减数列

下面用数学归纳法证明：

（1）当n=1时，已证命题成立（2）假设当n=k时命题成立，即x2k>x2k+2

112k+3?x2k+1

2k+2?x2k+4=x

易知x2k>0x

，那么1+x?=

2k+11+x2k+3(1+x2k+1)(1+x2k+3)

x2k?x2k+2

)(1+x>0

=(1+x2k2k+1)(1+x2k+2)(1+x2k+3)

即x2(k+1)>x2(k+1)+2

也就是说，当n=k+1时命题也成立，结合（1）和（2）知，命题成立

x

（2）当n=1时，n+1?xn=x2?x1=1

6，结论成立

11

?1<1,∴1+xn?1<2,xn=

当n≥20<xn

时，易知1+x>n?12

∴(1+xn)(1+xn?1)=(1+1

1+x+x5

n?1)=2+xn?1≥n?12

∴x=11xn?xn?1

n+1?xn1+x?=

n1+xn?1(1+xn)(1+xn?1)

24

≤2222n-1xn?xn?1≤（xn?1?xn?2≤…≤（）x2?x1555

12n-1=65

35.（2009天津卷理）已知等差数列{an}的公差为d（d≠0），等比数列{bn}的公比为q（q>1）sabab。设n=11+22…..+anbn

若n?1Tabab)n1122,=-+…..+(-1anbn+,n∈Na1=b1=1，d=2，q=3，求S3的值；

2dq(1?q2n)

2+bST1?q12n2n若=1，证明（1-q）-（1+q）=，n∈N；

(Ⅲ)若正数n满足2≤n≤q，设k1,k2,...,kn和l1,l2,...,ln是1，2...，，n的两个不同的排列，c1=ak1b1+ak2b2+...+aknbn，

c1≠c2c2=al1b1+al2b2+...+alnbn证明。

本小题主要考查等差数列的通项公式、等比数列的通项公式与前n项和公式等基础知识，考查运算能力，推理论证能力及综合分析和解决问题的能力的能力，满分14分。

n?1*a=2n?1,b=3,n∈Nn（Ⅰ）解：由题设，可得n

所以，S3=a1b1+a2b2+a3b3=1×1+3×3+5×9=55

n?1b=qn（Ⅱ）证明：由题设可得则

S2n=a1+a2q+a3q2+.....+a2nq2n?1,

T2n=a1?a2q+a3q2?a4q3+.....?a2nq2n?1,

S2n?T2n=2(a2q+a4q3+...?a2nq2n?1)

式减去②式，得

式加上②式，得①②

S2n+T2n=2(a1+a3q2+....+a2n?1q2n?2)

式两边同乘q，得③

q(S2n+T2n)=2(a1q+a3q3+....+a2n?1q2n?1)

所以，

(1?q)S2n?(1+q)T2n=(S2n?T2n)?q(S2n+T2n)

25

=2d(q+q3+K+q2n?1)

=2dq(1?q2n)

?q,n∈N*

12

(Ⅲ)证明：c1?c2=(ak1?al1)b1+(ak2?al2)b2+K+(akn?aln)bn

=(k1?l1)db1+(k2?l2)db?1

1q+K+(kn?ln)db1qn

因为d≠0,b1≠0,所以

c1?c2=(k1?l1)+(k2?l2)q+K+(k?1

dbn?ln)qn

1

若kn≠ln，取i=n

若kn=ln，取i满足ki≠li且kj=lj,i+1≤j≤n

由（1）,(2)及题设知，1<i≤n且

c1?c2=(k1?l1)+(k2?l2)q+K(k2

i?1?li?1)qi?+(ki?li)qi?1

db1

当ki<li时，得ki?li≤?1,由q≥n，得ki?li≤q?1,i=1,2,3.....i?1

即k1?l1≤q?1，(k2?l2)q≤q(q?1)…，(ki?1?li?1)qi?2≤qi?2(q?1)

又(ki?li)qi?1≤?qi?1,所以

c1?c2

db=(q?1)+(q?1)q+K(q?1)qi?2?qi?1=(q?1)1?qi?1

11?q

因此c1?c2≠0,即c1≠c2

c1?c2

当ki>l<?1

i同理可得db1，因此c1≠c2

综上，c1≠c2

37.（20xx年上海卷理）已知{an}是公差为d的等差数列，{bn}是公比为q的等比数列。若an=3n+1，是否存在m、k∈N*，有am+am+1=ak?说明理由；

an+1

找出所有数列{a}=bn

n和{bn}，使对一切n∈N*,an,并说明理由；

26

若a1=5,d=4,b1=q=3,试确定所有的p，使数列{an}中存在某个连续p项的和是数列{bn}中的一项，请证明。

am+am+1=ak，得6m+5=3k+1，

4

3，∵m、k∈N?，∴k?2m为整数，

．．．．．．5分．．．．．．2分[解法一]（1）由k?2m=整理后，可得?∴不存在m、k∈N，使等式成立。

an+1a1+nd=bn=b1qn?1

（2）若a，即a1+(n?1)d，

1=b1q（ⅰ）若d=0,则

当{n?1（*）=bn。．．．．．．7分an}为非零常数列，{bn}为恒等于1的常数列，满足要求。

lima1+nd=1n→∞a+(n?1)d1（ⅱ）若d≠0，（*）式等号左边取极限得，（*）式等号右边的极限只有当q=1时，才能等于1。

此时等号左边是常数，∴d=0，矛盾。

综上所述，只有当{an}为非零常数列，{bn}为恒等于1的常数列，满足要求。．．．．．．10分an+1=bn,且{bn}为等比数列anan=nd+c,若【解法二】设

an+2an+1/=q,对n∈N*都成立，即anan+2=qa2

n+1

则an+1an

∴(dn+c)(dn+2d+c)?q(dn+d+c)2对n∈N*都成立，∴a2=qd2....7分

*a=c≠0,∴b=1,n∈Nnn若d=0，则

dn+d+c=m∴b=md≠0,则q=1,ndn+c若（常数）即，则d=0，矛盾an=c≠0,bn=1,使对一切n∈N*,

综上所述，有

na=4n+1,b=3,n∈N*nn（3）an+1=bnan，10分

设am+1+am+2+……+am+p=bk=3k,p、k∈N*,m∈N.

4(m+1)+1+4(m+p)+1p=3k

2，

27

3k

∴4m+2p+3=,∵p、k∈N*,∴p=35,s∈Np.

2s+2s2s+2sk=3s+2,4m=3?2×3?3=(4?1)?2×(4?1)?3?0,取13分15分

由二项展开式可得正整数M1、M2，使得（4-1）2s+2=4M1+1,

2×(4?1)s=8M2+(?1)s2,

∴4m=4(M1?2M2)?((?1)s+1)2,∴存在整数m满足要求.

故当且仅当p=3s,s∈N时，命题成立.

说明：第（3）题若学生从以下角度解题，可分别得部分分（即分步得分）若p为偶数，则am+1+am+2+……+am+p为偶数，但3k为奇数

故此等式不成立，所以，p一定为奇数。

当p=1时，则am+1=bk,即4m+5=3k，

而3k=(4-1)k

0k1k?1k?1k?1kkkC?4+C?4?(?1)+……+C?4?(?1)+C?(?1)=4M+(?1),M∈Z,kkk=k

当ｋ为偶数时，存在ｍ，使４ｍ＋５＝3k成立1分当p=3时，则am+1+am+2+am+3=bk,即3am+2-bk,

也即3（4m+9）=3k,所以4m+9=3k-1,4(m+1)+5=3k-1

由已证可知，当k-1为偶数即k为奇数时，存在m,4m+9=3k成立2分当p=5时，则am+1+am+2+……+am+5=bk,即5am+3=bk

也即5（4m+13）=3k,而3k不是5的倍数，所以，当p=5时，所要求的m不存在故不是所有奇数都成立.2分

三、解答题

{a}0<a1<1，an+1=f(an)．10.（2008全国I）设函数f(x)=x?xlnx．数列n满足

1)是增函数；（Ⅰ）证明：函数f(x)在区间(0，

（Ⅱ）证明：an<an+1<1；

k≥a1?b

a1lnb．证明：ak+1>b．（Ⅲ）设b∈(a1，1)，整数

f'(x)=?lnx,当x∈(0,1)时，f'(x)=?lnx>0（Ⅰ）证明：f(x)=x?xlnx，

故函数f(x)在区间(0,1)上是增函数；

（Ⅱ）证明：（用数学归纳法）（i）当n=1时，0<a1<1，a1lna1<0，a2=f(a1)=a1?a1lna1>a1

1)是增函数，且函数f(x)在x=1处连续，则f(x)在区间(0，1]是增函数，由函数f(x)在区间(0，

28

a2=f(a1)=a1?a1lna1<1，即a1<a2<1成立；

（ⅱ）假设当x=k(k∈N*)时，ak<ak+1<1成立，即0<a1≤ak<ak+1<1

1]是增函数，0<a1≤ak<ak+1<1得那么当n=k+1时，由f(x)在区间(0，

f(ak)<f(ak+1)<f(1).而an+1=f(an)，则ak+1=f(ak),ak+2=f(ak+1)，

ak+1<ak+2<1，也就是说当n=k+1时，an<an+1<1也成立；

根据（ⅰ）、（ⅱ）可得对任意的正整数n，an<an+1<1恒成立.

a=f(an)可（Ⅲ）证明：由f(x)=x?xlnx．n+1

=a1?b?∑ailnai

i=1kak+1?b=ak?b?aklnak

若存在某i≤k满足

若对任意i≤k都有

kai≤b，则由⑵知：ak+1?b<ai?b≥0ai>b，则ak+1?b=ak?b?aklnakkk

=a1?b?∑ailnai=a1?b?∑ailnb=a1?b?(∑ai)lnb

i=1i=1i=1>a1?b?ka1lnb

≥a1?b?ka1lnb>a1?b?(a1?b)=0，即ak+1>b成立.

11.（2008山东卷)将数列｛an｝中的所有项按每一行比上一行多一项的规则排成如下数表：a1

a2a3

a4a5a6

a7a8a9a10

……

2bn

2bS?SnnN记表中的第一列数a1，a2，a4，a7，…构成的数列为｛bn｝,b1=a1=1.Sn为数列｛bn｝的前n项和，且满足＝1=

（n≥2）.

1

S(Ⅰ)证明数列｛n｝成等差数列，并求数列｛bn｝的通项公式；

（Ⅱ）上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数.当求上表中第k(k≥3)行所有项和的和.a81=?491时，

xA(a，b)a=a，Sn是数列{an}的前n项和，且满足y=ennnn∈N*12.(2007湖南)已知（）是曲线上的点，1

29

22Sn=3n2an+Sn?1，an≠0，n=2，3，4…．，

?bn+2???b（I）证明：数列?n?（n≤2）是常数数列；

（II）确定a的取值集合M，使a∈M时，数列

（III）证明：当a∈M时，弦{an}是单调递增数列；AnAn+1（n∈N*）的斜率随n单调递增

222S?S=3nan．n≥2nn?1解：（I）当时，由已知得

2a=S?S≠0S+S=3nnnn?1nn?1因为，所以．

2S+S=3(n+1)n+1n于是．……①……②

……③

……④

……⑤由②－①得于是an+1+an=6n+3．an+2+an+1=6n+9．an+2?an=6，由④－③得

?bn+2?bn+2ean+2an+2?an6=an=e=e??(n≥2)bbe所以n，即数列?n?是常数数列．

（II）由①有S2+S1=12，所以a2=12?2a．由③有a3+a2=15，a4+a3=21，所以a3=3+2a，a4=18?2a．

{a2k}和{a2k+1}分别是以a2，a3为首项，6为公差的等差数列，而⑤表明：数列

所以

数列a2k=a2+6(k?1)，a2k+1=a3+6(k?1)，a2k+2=a4+6(k?1)(k∈N*)，{an}是单调递增数列?a1<a2且a2k<a2k+1<a2k+2对任意的k∈N*成立．

?a1<a2且a2+6(k?1)<a3+6(k?1)<a4+6(k?1)

915?a<12?2a<3+2a<18?2a?<a<?a1<a2<a3<a444．

?915?M=?a<a<?4?．?4即所求a的取值集合是

bn+1?bnean+1?eankn==AAan+1?anan+1?an（III）解法一：弦nn+1的斜率为

ex(x?x0)?(ex?ex0)ex?ex0f(x)=f(x)=2xx?x(x?x)00，则0任取，设函数

30

x0xx′(x)=ex(x?x0)+ex?ex=ex(x?x0)g(x)=e(x?x)?(e?e)g0记，则，

当

当x>x0时，g′(x)>0，g(x)在(x0，+∞)上为增函数，x<x0时，g′(x)<0，g(x)在(?∞，x0)上为减函数，

x≠x0时，g(x)>g(x0)=0，从而f′`(x)>0，所以f(x)在(?∞，x0)和(x0，+∞)上都是增函数．

{an}单调递增，所以由（II）知，a∈M时，数列

ean+1?eanean+2?eankn=<x=aa<a<aa?aan+2?an．n，因为nn+1n+2，所以n+1n取0

ean+1?ean+2ean?ean+2kn+1=>x=an+2，因为an<an+1<an+2，所以an+1?an+2an?an+2．取0

所以kn<kn+1，即弦AnAn+1(n∈N*)的斜率随n单调递增．ex?ean+1f(x)=+∞)上都是增函数，x?an+1，同解法一得，f(x)在(?∞，an+1)和(an+1，解法二：设函数

ean?ean+1ex?ean+1ean+2?ean+1ex?ean+1an+1an+1kn=<lim=ek=>lim=en+1+n→a?n→ana?aa?a+1x?an+1x?an+1nn+1n+2n+1n+1所以，．

故kn<kn+1，即弦AnAn+1(n∈N*)的斜率随n单调递增．

1222+4=1,记S=a+a+?+an12n,2an5.（辽宁省沈阳二中2008—2009学年上学期高三期中考试）{an}满足a1=1,an+1数列

m的最小值

A．10B．9

答案：A.若S2n+1?Sn≤m30对任意n∈N*恒成立，则正整数（）C．8D．7

31