数学实验报告

实验人员：院（系）   学号         姓名 

实验地点：计算机中心机房

实验一

实验名称：无穷级数与函数逼近

实验时间：　20##　年　6月  3日

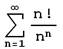
实验目的：观察的部分和序列的变化趋势，并求和

实验内容：

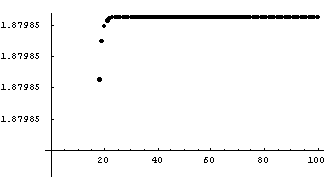
（1）利用级数观察图形的敛散性

当n从1~400时，输入语句如下：

运行后见下图，可以看出级数收敛，级数和大约为1.87985

（2）求和

先输入：

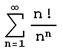
输出：

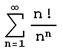
输出和输入相同，此时应该用近似值法。输入：

输出：

1.87985

结论：级数大约收敛于1.87985

实验心得：

通过求的部分和序列与和，我学会了运用“Table”命令生成部分和序列的变化趋势，也学会了如何提高精度作图以及如何用不同方法求一个函数的和。这些都对判断一个级数的各方面性质有重要帮助。

实验二

实验名称：最小二乘法

实验时间：　　20##年　6月  3日

实验目的：测定某种刀具的磨损速度与时间的关系

实验内容：

（1）       确定函数的类型

为此，我们将所有数据输入电脑，作出散点图。输入语句如下：

t={0,1,2,3,4,5,6,7};

y={27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8};

ty=Table[{t[[i]],y[[i]]},{i,1,8}]

ListPlot[ty,PlotStyle®PointSize[0.02]]

运行后可得数据表和下图：

{{0,27.},{1,26.8},{2,26.5},{3,26.3},{4,26.1},{5,25.7},{6,25.3},{7,24.8}}

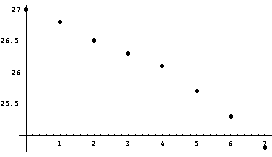
从图中可以看出这些点近似的落在一条直线周围，可以认为x和y之间存在线性关系，之所以不完全落在直线上，是因为数据本身存在误差。下面用最小二乘法球处于这些数据点最接近的直线方程。

（2）       求最小二乘解

设直线方程y=at+b，其中，a，b是待定系数。输入语句：

x={0,1,2,3,4,5,6,7};

y={27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8};

xy=Table[{x[[i]],y[[i]]},{i,1,8}];

q[a_,b_]:=Sum[(a*x[[i]]+b-y[[i]])^2,{i,1,8}]

Solve[{D[q[a,b],a]?0,D[q[a,b],b]?0},{a,b}]

运行后得：

{{a®-0.303571,b®27.125}}

（3）       比较拟合函数与已知数据点

在同一坐标系下绘出数据点的散点图及拟合函数的图形，输入语句如下：

x={0,1,2,3,4,5,6,7};

y={27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8};

xy=Table[{x[[i]],y[[i]]},{i,1,8}];

q[a_,b_]:=Sum[(a*x[[i]]+b-y[[i]])^2,{i,1,8}]

Solve[{D[q[a,b],a]?0,D[q[a,b],b]?0},{a,b}]

t1=ListPlot[xy,PlotStyle®PointSize[0.02]];

f[x_]:=-0.30357*x+27.125;

t2=Plot[f[x],{x,0,10}];

Show[t1,t2]

运行结果为：

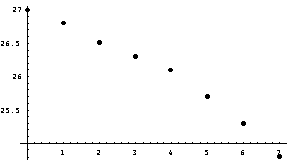
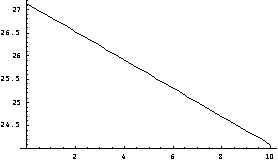
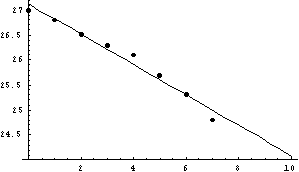
从图中可以看出，拟合曲线与散点图分布较为吻合，假设成立。

结论：刀具的磨损速度与时间的关系大致为：y=-0.303571x+27.125

实验心得：

生活中常用到最小二乘法。我们知道许多关于两个相关变量的数据之后，通过数学方法求解即可得到结论。且我学会了散点图与拟合函数放在同一坐标系中观察是否吻合，这对判断初始假设是否正确十分重要。如果偏差过大，就要考虑是否是模型建错了。

通过两个实验，我体会到做题一定要认真。一不小心就可能把大写弄成小写，或者落了分号，都会导致程序调试不出来。做题要有耐心。

 

第二篇：东南大学高等数学(下册)数学实验报告

10-11-3学期高等数学数学实验报告

实验人员：院（系）

学号： 姓名        成绩_________

实验时间：20##年5月28日

实验一

1.      作出各种标准二次曲面的图形。

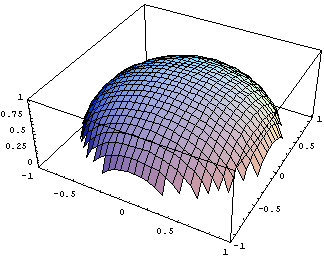
（1）    球面

·程序设计：

·程序运行结果：

（2）   （椭）圆抛物面

·程序设计：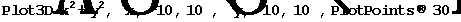

·程序运行结果：

（3）   圆锥面

·程序设计：

·程序运行结果：

（4）   马鞍面

·程序设计：

·程序运行结果：

实验二

利用参数方程作图，作出由下列曲面所围成的立体：

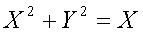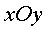（1）  ， 及面

·程序设计：

s1=ParametricPlot3D[{Sin[z]*Cos[u],Sin[z]*Sin[u],Cos[z]},{z,0,Pi/2},{u,0,2Pi},PlotRange?{-1,1},AxesLabel?{"x","y","z"},DisplayFunction?Identity];

s2=ParametricPlot3D[{1/2*Cos[u]+1/2,1/2*Sin[u],v},{u,-Pi,Pi},{v,0,1},AxesLabel?{"x","y","z"},DisplayFunction?Identity];

s3=ParametricPlot3D[{u,v,0},{u,-1,1},{v,-1,1},AxesLabel?{"x","y","z"},

DisplayFunction?Identity];

Show[s1,s2,s3,DisplayFunction?$DisplayFunction]

·程序运行结果 ：

       

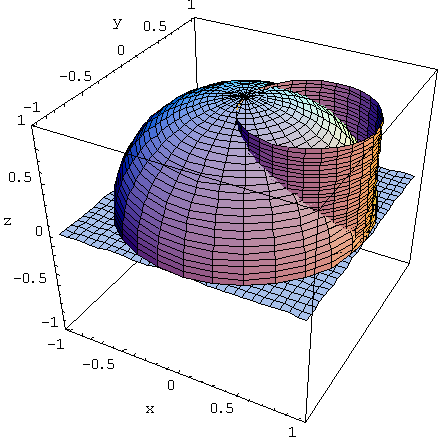
·程序截图：

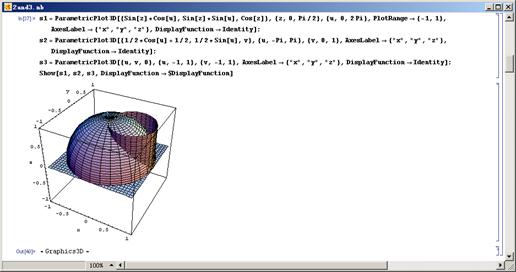
实验三：

2.      改变例2中m的值及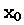的数值来求函数的幂级数及观察其幂级数逼近函数的情况

·程序设计：

·程序运行结果：