第五章 定积分总结
第五章 定积分 总结
一、定积分的概念与结论
1.定积分的概念
(1)定积分的定义: .
(2)定积分的基本思想: .
(3)两个规定:① ;②
(4)定积分的值只与积分区间和被积函数有关,与积分变量的选取 关.
(5)可积的条件:
① ;② .
(6)定积分的几何意义:
①
;
②
;
③
.
2.积分上限函数: .
积分上限函数的导数: .
3.广义积分
(1)无穷区间上的广义积分:
 = ;
= ;
 = ;
= ;
 = .
= .
(2)无界函数的广义积分
设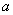 为
为 的瑕点,
的瑕点,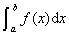 = ;
= ;
设 为
为 的瑕点,
的瑕点,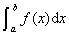 = ;
= ;
设 ,
,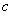 为
为 的瑕点,
的瑕点,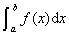 = .
= .
二、定积分的性质
性质1: .
性质2: .
性质3: .
性质4: .
性质5: .
推论1: ;推论2: .
性质6: .
性质7: .
三、定积分的计算方法
1.牛顿——莱布尼兹公式: .
2.第一类换元积分公式(凑微分公式): .
3.第二类换元积分公式: .
4.分部积分公式: .
5.利用奇偶性计算定积分:
(1)若 在
在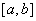 上连续且为偶函数,则
上连续且为偶函数,则 .
.
(2)若 在
在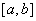 上连续且为奇函数,则
上连续且为奇函数,则 .
.
6.一个重要的积分公式:
 为正的偶数时,
为正的偶数时, ;
;
 为大于1的奇数时,
为大于1的奇数时, .
.
四、定积分的应用
1.平面图形的面积:
(1)若平面图形由连续曲线 及直线
及直线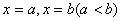 所围成,则其面积为
所围成,则其面积为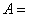 .
.
(2)若平面图形由连续曲线 及直线
及直线 所围成,则其面积为
所围成,则其面积为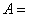 .
.
2.旋转体的体积:
(1)由连续曲线 ,直线
,直线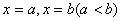 及
及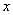 轴所围成的平面图形绕
轴所围成的平面图形绕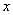 轴旋转一周而成的旋转体的体积为
轴旋转一周而成的旋转体的体积为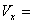 .
.
(2)由连续曲线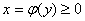 ,直线
,直线 及
及 轴所围成的平面图形绕
轴所围成的平面图形绕 轴旋转一周而成的旋转体的体积为
轴旋转一周而成的旋转体的体积为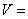 .
.
3.定积分在经济问题中的应用:
.
第二篇:高等数学第五章_定积分总结
第五章 定积分
创新生技102班 张梦菲
2010015066
一、 主要内容
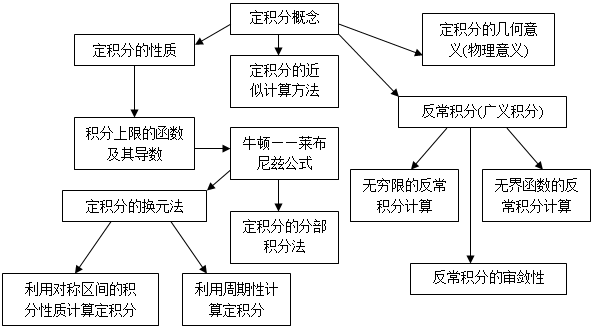
Ⅰ. 定积分概念:
- 定积分定义:设
 在区间
在区间 上有界,在
上有界,在 中任意插入若干个分点
中任意插入若干个分点
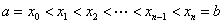 .把
.把 分成
分成 个小区间
个小区间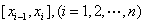 ,小区间的长度记为
,小区间的长度记为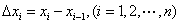 ,在
,在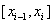 上任意取一点
上任意取一点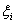 ,作
,作 ,若
,若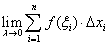
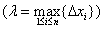 存在. 就称该极限为
存在. 就称该极限为 在
在 上的定积分.
上的定积分.
记为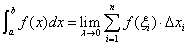
当上述极限存在时,称 在
在 上可积.
上可积.
- 若
 在
在 上连续,则
上连续,则 在
在 上可积。
上可积。 - 若
 在
在 上有界,且只有有限个间断点,则
上有界,且只有有限个间断点,则 在
在 上可积.
上可积.
Ⅱ. 定积分的几何意义
定积分 在几何上表示:由曲线
在几何上表示:由曲线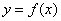 ,直线
,直线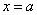 和
和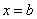 以及
以及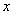 轴所围图形面积的代数和 (
轴所围图形面积的代数和 (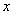 轴上方的面积取正,
轴上方的面积取正,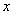 轴下方的面积取负)
轴下方的面积取负)
Ⅲ. 定积分的性质
1. 补充规定:(1)当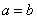 时,
时,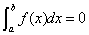
(2)当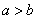 时,
时, 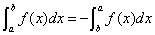
2. 性质:
(1) 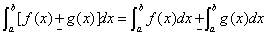
(2) 
(3) 
(4)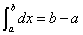
(5) 若在 上,
上,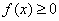 ,则
,则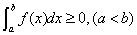
推论1:若在 上,
上,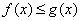 ,则
,则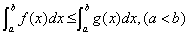 .
.
推论2: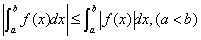 .
.
(6 ) 若在 上,
上, ,则
,则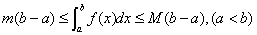
(7) (定积分中值定理):若 在
在 上连续,则在
上连续,则在 上至少存在
上至少存在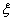 ,使
,使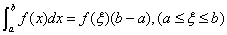 .
.
3. 连续函数 在
在 上的平均值,
上的平均值,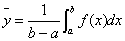
Ⅳ. 积分上限函数及其导数
1. 若对任意 ,
,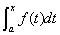 存在,则称
存在,则称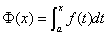 为积分上限的函数.
为积分上限的函数.
2. 若 在
在 上可积,则
上可积,则 在
在 上有界. 且积分上限函数
上有界. 且积分上限函数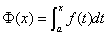 在
在 上连续.
上连续.
3. 设 在
在 上连续,则
上连续,则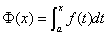 在
在 上可导,且
上可导,且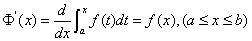 .
.
4. 设 连续,
连续, 可导,则
可导,则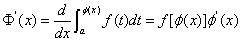 .
.
5. 设 连续,
连续, ,
,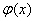 可导,则
可导,则
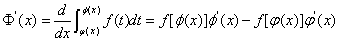 .
.
Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)
设 在
在 上连续,
上连续,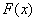 为
为 在
在 上的一个原函数,则
上的一个原函数,则
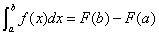 .
.
Ⅵ. 定积分的换元法
设 在
在 上连续,
上连续,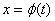 满足:
满足:
(1)  .
.
(2)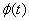 在
在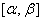 (或
(或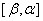 )上具有连续导数,且
)上具有连续导数,且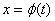 的值域不越出
的值域不越出 的范围,则有
的范围,则有 .
.
注:当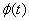 的值域
的值域 越出
越出 的范围,但满足其余条件时,只要
的范围,但满足其余条件时,只要 在
在 上连续,则换元法的结论仍然成立.
上连续,则换元法的结论仍然成立.
Ⅶ. 定积分的分部积分法
设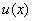 与
与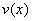 在
在 上具有连续导数,则有
上具有连续导数,则有
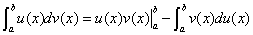
Ⅷ. 几类特殊的积分公式
1. 设 在
在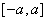 上连续,则有
上连续,则有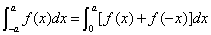 .
.

2. 设 是以
是以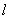 为周期的连续函数,则对任意实数
为周期的连续函数,则对任意实数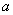 ,
,
有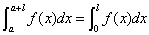 .
.
3. 设 在
在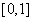 上连续,则
上连续,则
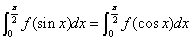

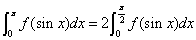
4. 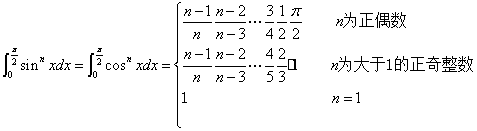
Ⅸ. 反常积分(广义积分)
1. 无穷限的反常积分
(1) 设 在
在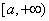 上连续,
上连续, 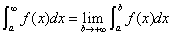
(2) 设 在
在 上连续,
上连续, 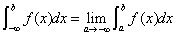
(3) 设 在
在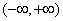 上连续,
上连续,
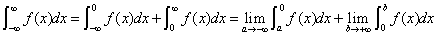
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有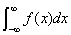 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在,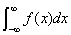 就发散.
就发散.
2. 无界函数的反常积分
(1) 设 在
在 上连续,点
上连续,点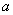 为
为 的瑕点,
的瑕点,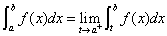
(2) 设 在
在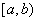 上连续,点
上连续,点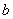 为
为 的瑕点,
的瑕点,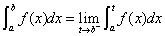
(3) 设 在
在 上除点
上除点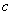
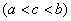 外连续,点
外连续,点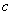 为
为 的瑕点,
的瑕点,
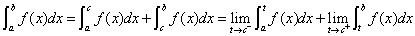
若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散.
注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有 收敛. 只要有一个极限不存在,
收敛. 只要有一个极限不存在, 就发散.
就发散.
3. 反常积分的审敛法
(1) (比较审敛法1) 设 在
在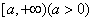 上连续,且
上连续,且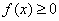 . 若存在常数
. 若存在常数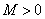 及
及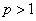 ,使得
,使得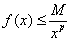
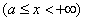 ,则反常积分
,则反常积分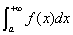 收敛;若存在常数
收敛;若存在常数 ,使得
,使得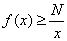
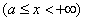 ,则反常积分
,则反常积分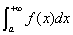 发散.
发散.
(2) (极限审敛法1) 设 在
在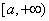 上连续,且
上连续,且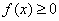 . 若存在常数
. 若存在常数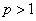 ,使得
,使得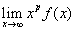 存在,则反常积分
存在,则反常积分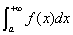 收敛;若
收敛;若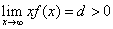 ,
,
(或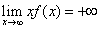 )则反常积分
)则反常积分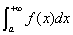 发散.
发散.
(3) (比较审敛法2)设 在
在 上连续,且
上连续,且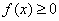 .
. 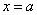 为
为 的瑕点.若存在常数
的瑕点.若存在常数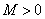 及
及 ,使得
,使得 ,则反常积分
,则反常积分 收敛;若存在常数
收敛;若存在常数 ,使得
,使得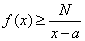
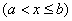 ,则反常积分
,则反常积分 发散.
发散.
(4) (极限审敛法2) 设 在
在 上连续,且
上连续,且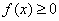 .
. 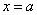 为
为 的瑕点. 若存在常数
的瑕点. 若存在常数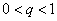 ,使得
,使得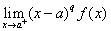 存在,则反常积分
存在,则反常积分 收敛;若
收敛;若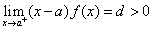 ,(或
,(或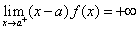 )则反常积分
)则反常积分 发散.
发散.
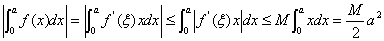 .
.
-
第五章 定积分总结
第五章定积分总结一、定积分的概念与结论1.定积分的概念(1)定积分的定义:.(2)定积分的基本思想:.(3)两个规定:①;②(4)…
-
定积分的方法总结
定积分的方法总结定积分是新课标的新增内容其中定积分的计算是重点考查的考点之一下面例析定积分计算的几种常用方法一定义法例1求basi…
-
定积分总结
康博思优立中学教育高中数学定积分讲义总结内容一定积分概念一般地设函数fx在区间ab上连续用分点ax0x1x2将区间ab等分成n个小…
-
七大积分总结
七大积分总结一定积分1定积分的定义设函数fx在ab上有界在区间ab中任意插入n1个分点ax0ltx1ltx2ltltxi1ltxi…
-
定积分计算的总结论文
定积分计算的总结闫佳丽摘要本文主要考虑定积分的计算对一些常用的方法和技巧进行了归纳和总结在定积分的计算中常用的计算方法有四种1定义…
-
高数积分总结
第四章一元函数的积分及其应用第一节不定积分一、原函数与不定积分的概念定义1.设f(x)是定义在某区间的已知函数,若存在函数F(x)…
-
积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
高等数学第五章_定积分总结
第五章定积分创新生技102班张梦菲20xx015066一、主要内容Ⅰ.定积分概念:1.定积分定义:设f(x)在区间[a,b]上有界…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
明贤学校20xx-20xx学年度第一学期904班班主任安全工作总结
班主任:李海彬九年级4班电话:136xxxxxxxx明贤学校20xx-20xx学年度第一学期班主任安全工作总结班级:904班班主任…