数学归纳法、极限 （一）第一数学归纳法：

一般地，证明一个与自然数n有关的命题P(n），有如下步骤：

（1）证明当n取第一个值n0时命题成立。n0对于一般数列取值为0或1，但也有特殊情况；

（2）假设当n=k（k≥n0，k为自然数）时命题成立，证明当n=k+1时命题也成立。

综合（1）（2），对一切自然数n（≥n0），命题P(n）都成立。

（二）第二数学归纳法：

对于某个与自然数有关的命题P(n），

（1）验证n=n0时P(n）成立；

（2）假设n0≤n<=k时P(n）成立，并在此基础上，推出P(k+1）成立。

综合（1）（2），对一切自然数n（≥n0），命题P(n）都成立。

（三）倒推归纳法（反向归纳法）：

（1）验证对于无穷多个自然数n命题P(n）成立（无穷多个自然数可以是一个无穷数列中的数，如对于算术几何不等式的证明，可以是2^k，k≥1）；

（2）假设P(k+1）（k≥n0）成立，并在此基础上，推出P(k）成立， 综合（1）（2），对一切自然数n（≥n0），命题P(n）都成立；

（四）螺旋式归纳法

对两个与自然数有关的命题P(n），Q(n），

（1）验证n=n0时P(n）成立；

（2）假设P(k）（k>n0）成立，能推出Q(k）成立，假设 Q(k）成立，能推出 P(k+1）成立；

综合（1）（2），对一切自然数n（≥n0），P(n），Q(n）都成立。

1．数学归纳法用于证明一个“关于正自然数n的命题对于从正自然数n0

1 / 10

开始的所有正自然数n都成立”的问题。

2．能根据f(k)正确写出f(k+1),并能指出f(k)与f(k+1)之间的关系，这

往往是运用数学归纳法的最关键的一步。

[举例1]已知f(n)?

A．f(n)+1111，则f(n?1)= ?????n?1n?2n?32n111， B．f(n)++， 2(n?1)2n?12(n?1)

111 D．f(n)+- 2(n?1)2n?12(n?1)C．f(n)-

解析：f(n)是从n+1开始的n个连续自然数的倒数和，故f(n?1)是从

n+2开始的n+1个连续自然数的倒数和，即

f(n?1)=

=11111 ??????n?2n?3n?1?n?1n?1?nn?1?n?11111111=f(n)++-??????n?2n?32n2n?12(n?1)2n?12(n?1)

1 n?1

=f(n)+11- 故选D。 2n?12(n?1)

[举例2]用数学归纳法证明“5n－2n能被3整除”的第二步中，n=k+1时，为

了使用归纳假设，应将5k+1－2k+1变形为

[解析]假设n=k时命题成立.即:5k－2k 被3整除.当n=k+1时，5k+1－2 k+1 =5

×5k－2×2 k

=5(5k－2k) ＋5×2k－2×2k=5(5k－2k) ＋3×2k

[巩固1] 用数学归纳法证明1＋111＋＋…＋n<n (n>1)时，由n232?1

＝k (k>1)不等式成立，推证n＝k＋1时，左边应增加的代数式的个数是

_____。

A. 2k?1 B. 2－1 C. 2 D. 2＋1 kkk

[巩固2]用数学归纳法证明命题：

(n＋1) ×(n＋2) ×…×(n＋n)=2n×1×3×…×(2n－1)

2 / 10

3．数学归纳法公理：如果关于自然数n 的一个命题p(n)满足下列条件 (1) p(n0)成立,即当n=n0时,命题成立，(2) 假设p(k)成立,则p(k+1)也成立；根据(1)(2)知命题p(n)对n≥n0的所有自然数n都成立。用数学归纳法证明问题的过程实质上是一个递推的过程，（1）是递推的基础，（2）是递推的条件；二者缺一不可。

4．数学归纳法通常用于证明关于自然数n的等式、不等式、整除性等。用“归纳假设”即命题p(k)成立证明命题 p(k+1)成立（已知p(k)成立，求证p(k+1)成立）是数学归纳法证明中最关键的一步；而明晰命题p(k)与命题 p(k+1)之间的关系又是实现这一步的前提。

[举例1] 已知m为正整数，用数学归纳法证明：当x??1时，

m(1?x)≥1?mx；

解析：视(1?x)≥1?mx为关于m的不等式，x为参数，以下用数学归纳法证明：

（ⅰ）当m?1时，原不等式成立；当m?2时，左边?1?2x?x，右边2m?1?2x，

因为x2≥0，所以左边≥右边，原不等式成立；

k（ⅱ）假设当m?k时，不等式成立，即(1?x)

时， ≥1?kx，则当m?k?1

∵x??1，∴1?x?0，于是在不等式(1?x)k≥1?kx两边同乘以1?x得

(1?x)k·(1?x)≥(1?kx)(1?x)?1?(k?1)x?kx2≥1?(k?1)x， 所以(1?x)k?1≥1?(k?1)x．即当m?k?1时，不等式也成立． 综合（ⅰ）（ⅱ）知，对一切正整数m，不等式都成立．

*[举例2]设正整数数列?an?满足：a2?4，且对于任何n?N，有

3 / 10

11?aan?111（1）求a1，a3；（2）求数列?an?的通项an． 2??n?2?；an?11?1an

nn?1

（07高考江西理22）

解析：（1）据条件得2??111?1?n(n?1)????2? ① an?1an?anan?1?

2??11???a2?a1?1????a2，当n?1时，由1即a1有

2?1221???2?， 4a14a1

解得28?a1?．因为a1为正整数，故a1?1． 37

?11?11?6????2?，解得8?a3?10，所以a34?4a3?当n?2时，由2?

a3?9．

（2）由a1?1，a2?4，a3?9，猜想：an?n．

下面用数学归纳法证明．

?1当n?1，2时，由（1）知an?n均成立；

?2假设n?k(k≥2)成立，则ak?k，则n?k?1时 222

由①得2??111?1?k(k?1)?2??2??2ak?1kakk?1??

k2(k?1)k(k2?k?1)?2?ak?1? k?k?1k?1

4 / 10

(k?1)21 ?(k?1)?2?ak?1?(k?1)2?k?1k?12

因为k≥2时，(k?1)?(k?1)?k(k?1)(k?2)≥0，所以22

(k?1)2

??0，1?． 2k?1

k?1≥1，所以1??0，1?k?1．又ak?1?N*，所以(k?1)2≤ak?1≤(k?1)2．

??故ak?1?(k?1)，即n?k?1时，an?n成立．由1，2知，对任意22

n?N*，an?n2．

[巩固1]已知数列8·n8·18?2，，…，2222，…；Sn221·3(2n?1)·(2n?1)3?5

为其前n项和，求S1、S2、S3、S4，推测Sn，并用数学归纳法证明。

[巩固2] 已知各项均为正数的数列?an?的前n项和Sn满足S1?1，且6Sn?(an?1)(an?2)，n?N．（Ⅰ）求?an?的通项公式；

（Ⅱ）设数列?bn?满足an(2n?1)?1，并记Tn为?bn?的前n项和，求证： b

3Tn?1?log2(an?3)，n?N （07高考重庆理21）

5．若f(c)存在，则limf(x)=f(c)，若f(c)=g(c)=0，则limx?cx?cf(x)一g(x)

limg(x)=B，般“约分”（约去含x?c的因式）后再求极限。若limf(x)=A、x?cx?c

则lim[f(x)±g(x)]= A±B, lim[f(x)g(x)]=AB, limx?cx?cx?cf(x)A= g(x)B

5 / 10

(B≠0).

1??2x?1[举例] lim?2???（07高考陕西理13） x?1?x?1?x?x?2

解析：x?12x?111==， ?x2?x?2x?1(x?2)(x?1)x?2

111??2x?1∴lim?2= ???limx?1?x?1x?23x?1?x?x?2

[巩固1] 下列四个命题中，不正确的是（ ） ．．．

A．若函数f(x)在x?x0处连续，则lim?f(x)?lim?f(x) x→x0x→x0

B．函数f(x)?x?2的不连续点是x?2和x??2 2x?4

x→?x→?x→?il()fmilx(?)C．若函数f(x)，则mg(x)满足lim[f(x)?g(x)]?0，gx

D

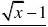
．x→11? （07高考湖南理7） 2

x??2[巩固2] lim(41?)?________ 4?x22?x

n

n??n??mil6．若|q|<1,则limq=0；则q=1，

不存在。limc n??nqn=1；若q>1或q≤-1, 则limqn??

cc? ”型的式子极限为0；“”型、“”型的极限不0?c

0?存在；“”型和“”型，一般分子、分母“同除以”一个式子（包括0?=c(c为常数)；“

“约分”）后再求极限；含有根式的和（差）的式子一般有理化后再求极限。若liman=A、limbn=B，则 lim(an±bn)= A±B, lim(anbn)=AB, n??n??n??n??

limn??anA= (B≠0). bnB

6 / 10

[举例1]

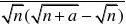
若n?1,则常数a? . 解析：分母有理化

1??1) nnan??1??2?1?a?2 a

[举例2]已知p和q是两个不相等的正整数，且q≥2，则

?1??1???1n?lim??（ ） qn→??1??1???1?n?

A．0 B．1 C．pp q D．p?1 （07高q?1考湖北理5） ?1?121?p??Cp?1???1nn?解析：limlimqn→?n??12?1?1?q??C1??1q??n?n?p1p???Cp2n1q???Cqn21?1np 1?1qn

121p1?Cp???Cp2pn=limn??121q1q??Cq???Cqnn2nq

1121pp?Cp?C3???Cpp2p?1pnnn=，选C。 limn??1q2131qq?Cq?Cq???Cqnn2nq?1p?

2n=[巩固1]把1?(1?x)?(1?x)???(1?x)展开成关于x的多项式，其各

项系数和为an，则lim2an?1等于（ ） n→?a?1n

7 / 10

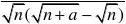
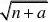
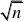
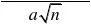
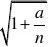
A．1 4 B．1 2 C．1 D．2

[巩固2]. nlim→∞1等于( ) 2n(n+1－n－1)

11 A. 1 B. C. D.0 24

an?1?abn?1

(?ax?b)?4[迁移]设正数a，b满足limx，则limn?1?nx?2n??a?2b2

（ ）

Ａ．0 Ｂ．1 4Ｃ．1 2

n??Ｄ．1 （07高考重庆理8） 7．无穷数列{an}的前n项和为Sn，limSn称为数列{an}的无穷多项和或

所有项和。求limSn时，切不可分别求各项的极限后再求和；必须先求Sn，n??

再求极限。若{an}为等比数列，公比为q且|q|<1，则limSn=n??a1。 1?q

[举例1]若数列{an}满足: a1?1, 且对任意正整数m,n都有3

am?n?am?an, 则

n???lim(a1?a2???an)? （07高考湖南理2）

A．123 B． C． 232

D．2

解析：数列{an}满足: a1?1, 且对任意正整数m,n都有am?n?am?an，3

111an?1?an?a1?an，∴数列{an}是首项为，公比为的等比数列。333

n???lim(a1?a2???an)?a11?，选A. 1?q2

2Q1 Q2 [巩固2]如图，抛物线y??x?1与x轴的正半轴交

8 / 10

Qn-1

O P1 P2 Pn-2 Pn-1

于点A，将线段OA的n等分点从左至右依次记为

P?，Pn?1，过这些分点分别作x轴的垂线， 1，P2，

?，Qn?1，从而得到n?1个直角三角形与抛物线的交点依次为Q1，Q2，

△Q2PP?，△Qn?1Pn?2Pn?1．当n??时，这些三角形的面积△Q1OP12，1，

之和的极限为 ．

12n?111,0)；Q1(,1?()2)，nnnnn

22n?1n?12Q2(,1?()2)，…，Qn?1(,1?())，记?QnPn?1Pn的面积为nnnn

1112Sn，则S1=??[1?()]，S2= 2nn

11211n?12，…，Sn-1=; ??[1?()2]??[1?()]2nn2nn解析：P1(,0)，P2(,0)，…，Pn?1(

lim(S1?S2???Sn?1)= n??

112?22???(n?1)21(n?1)(n?2)(2n?3)lim[(n?1)?]=?limn??2n2n??n212n3

=111?=. 263

1｝的前n项和为Sn，则limSn＝______________ 2n??4n－1[巩固1]数列｛[巩固2] 如图，等边三角形ABC的面积等于1，连结这个三角形各边的中

点得到一个小三角形，又连结这个小三角形各边的中点得到一个更小的 三角形，如此无限继续下去，求所有这些三角形的面积的和.

464646(?)?(2?2)?...?(n?n)?_____________ [巩固3]limn??(?)?(2?2)?...?(n?n)656565

9 / 10 C

答案

(2n?1)2?12、[巩固1]C；4、[巩固1] Sn＝，[巩固2] an?3n?1， (2n?1)2

5、[巩固1]C，[巩固2]固1] 1；6、[巩固1] D，[巩固2] B，[迁移] B；7、[巩41， 2

4[巩固2]，[巩固3] -1 3

10 / 10

 

第二篇：高二数学数学归纳法

1.4  数学归纳法

教学过程：

一、创设情境，启动思维

情境一、财主儿子学写字的笑话、“小明弟兄三个，大哥叫大毛……”的脑筋急转弯等；

教师总结：财主的儿子很傻很天真，但他懂一样思想方法，是什么？ 以上都是由特殊情况归纳出一般情况的方法---归纳法，这就是今天的课题. 人们通常也会用归纳法思考问题，小孩也会由此总结出什么年龄人该叫爷爷，什么年龄人叫阿姨，叫哥哥或姐姐.

情境二：华罗庚的“摸球实验”

1、这里有一袋球共12个，我们要判断这一袋球是白球，还是黑球，请问怎么判断？

启发回答:

方法一：把它全部倒出来看一看．特点：方法是正确的，但操作上缺乏顺序性．

方法二：一个一个拿，拿一个看一个．

比如结果为：第一个白球，第二个白球，第三个白球，……，第十二个白球，由此得到：这一袋球都是白球．特点：有顺序，有过程．

2、如果想象袋子有足够大容量，球也无限多？要判断这一袋球是白球，还是黑球，上述方法可行吗？

情境三: 回顾等差数列通项公式推导过程：

          

    设计意图：首先设计情境一,分析情境，自然引出课题----归纳法，谈笑间进入正题.再通过情境二的交流激发学生的兴趣，调动学生学习的积极性．情境三点出两种归纳法的不同特点.通过梳理我们熟悉的一些问题，很自然为本节课主题与重点引出打下伏笔.

二、师生互动，探究问题

承上启下：以上问题的思考和解决，用的都是归纳法.什么是归纳法？ 归纳法特点是什么？上述归纳法有什么不同呢？

学生回答以上问题，得出结论：

1. 归纳法：由一些特殊事例推出一般结论的推理方法.  特点：由特殊→一般；

2. 完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法；

3. 不完全归纳法: 根据事物的部分(而不是全部)特例得出一般结论的推理方法.

在生活和生产实际中，归纳法有着广泛的应用．例如气象工作者、水文工作者，地震工作者依据积累的历史资料作气象预测，水文预报，地震预测用的就是归纳法．

4. 引导学生举例：

    ⑴不完全归纳法实例：如欧拉发现立体图形的欧拉公式:(V为顶点数,E为棱数,F为面数)  

⑵ 完全归纳法实例： 如证明圆周角定理时，分圆心在圆周角内部、外部及一边上三种情况讨论．

    设计意图：从生活走向数学，与学生一起回顾以前学过的数学知识，并在这里我安排学生举完全归纳法的实例和不完全归纳法实例，进一步体会归纳意识，同时让学生感受到我们以前的学习中其实早已接触过归纳法，并引导学生积极投入到探寻论证方法过程的氛围中.

三 、借助史料, 引申思辨

问题1： 已知＝（n∈N），

(1) 分别求；；；．

(2) 由⑴你会有怎样的一个猜想？这个猜想正确吗？

问题2： 费马（Fermat）是17世纪法国著名的数学家，他是解析几何的发明者之一，是对微积分的创立作出贡献最多的人之一，是概率论的创始者之一，他对数论也有许多贡献．他曾认为，当n∈N时，一定都是质数，这是他对n＝0，1，2，3，4作了验证后得到的．后来，18世纪伟大的瑞士科学家欧拉（Euler）却证明了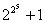＝4 294 967 297＝6 700 417×641，从而否定了费马的推测．没想到当n＝5这一结论便不成立．

教师总结: 有人说，费马为什么不再多算一个数呢？今天我们是无法回答的．但是要告诉同学们，失误的关键不在于多算一个数上！

问题3 ：, 当n∈N时，是否都为质数？

验证： f（0）＝41，f（1）＝43，f（2）＝47，f（3）＝53，f（4）＝61，f（5）＝71，f（6）＝83，f（7）＝97，f（8）＝113，f（9）＝131，f（10）＝151，…，f（39）＝1 601．但是f（40）＝1 681＝，是合数．

承上启下：这里算了39个数不算少了吧，但还是不行！我们介绍以上两个资料，不是说世界级大师还出错，我们有错就可以原谅，也不是说归纳法不行，不去学了，而是要找出运用归纳法出错的原因，并研究出对策来 , 寻求数学证明.

教师设问：,不完全归纳法为什么会出错？如何弥补不足？怎么给出证明呢？

设计意图：在生活引例与已学数学知识的基础上，进一步引导学生看数学史料，能够让学生多方位多角度体会归纳法，感受使用归纳法的普遍性．同时引导学生进行思辨：在数学中运用不完全归纳法常常会得到错误的结论，不管是我们还是数学大师都有可能如此．那么，不完全归纳法价值体现在哪里？不足之处如何去弥补呢？ 结论正确性怎样给出证明？学生一定会带着许多问题进入下一阶段探究.

四、实例再现，激发兴趣

1、演示多米诺骨牌游戏视频.

师生共同探讨多米诺骨牌全部依次倒下的条件：

 ⑴ 第一块要倒下; 

 ⑵ 当前面一块倒下时，后面一块必须倒下;

    当满足这两个条件后，多米诺骨牌全部都倒下.

再举例：再举几则生活事例：推倒自行车, 早操排队对齐等．

2、学生类比多米诺骨牌依顺序倒下的原理，探究出证明有关正整数命题的方法（建立数学模型）.

设计意图：布鲁纳的发现学习理论认为，“有指导的发现学习”强调知识发生发展过程．这里通过类比多米诺骨牌过程，让学生发现数学归纳法的雏形，是一种再创造的发现性学习．另外，这个环节里，我在培养学生大胆猜想、类比概括能力方面实践的不够好．应该让学生在类比多米诺骨牌游戏的基础上说出数学归纳法原理，教师给予肯定和补充即可。事实上，情境的设计都是为学生更好的知识迁移而服务的。概括能力是思维能力的核心．鲁宾斯坦指出：思维都是在概括中完成的．心理学认为“迁移就是概括”，这里知识、技能、思维方法、数学原理的迁移，突破口就是学生的概括过程．

五、类比联想，形成概念

1、 类比多米诺骨牌过程, 证明等差数列通项公式(师生共同完成,教师强调步骤及注意点)

(1) 当n＝1时等式成立；

(2) 假设当n＝k时等式成立, 即,

则=, 即n＝k＋1时等式也成立．

于是, 我们可以下结论： 等差数列的通项公式对任何n∈都成立．

2．数学归纳法原理(学生表述,教师补正)：

（1）（递推奠基）：n取第一个值(例如 )时命题成立；

（2）（递推归纳）：假设当n=k(k∈N^*，且k≥n₀)时结论正确；（归纳假设）

利用它证明当n=k+1时结论也正确.（归纳证明）

由(1)，(2)可知，命题对于从n₀开始的所有正整数n都正确，这种证明方法叫做数学归纳法．

3、数学归纳法的本质：无穷的归纳→有限的演绎（递推关系）

设计意图：至此，由生活实例出发，与学生一起解析归纳原理, 揭示递推过程.教师强调数学归纳法特点. 数学归纳法实际上是一种以数学归纳法原理为依据的演绎推理，它将一个无穷的归纳过程转化为一个有限步骤的演绎过程，是处理自然数有关问题的有力工具，一种具普遍性的方法.

六、讨论交流，深化认识

例1、 数列中, ＝1, (n∈), 通项公式是什么？你是怎么得到的？

探讨一：观察数列特点，变形解出.

探讨二：先计算，，的值，再推测通项的公式, 最后用数学归纳法证明结论．

设计意图：通过典型例题使学生探究尝试，一方面体验“观察—归纳—猜想—证明”完整过程，既能巩固归纳法和数学归纳法，也能使他们体验数学方法，培养学生独立研究数学问题的意识和能力．不同的方法也体现解决问题的灵活性.

七、反馈练习, 巩固提高

（请两位同学板演以下两题，教师指正）

1、用数学归纳法证明：1＋3＋5＋…＋（2n－1）＝．

2、首项是，公比是q的等比数列的通项公式是．

3、用数学归纳法证明： 时，下列推证是否正确，说出理由？

证明：假设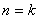时，等式成立

就是 成立

那么

        =

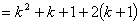这就是说当时等式成立，

所以时等式成立.

4、判断下列推证是否正确，若是不对，如何改正.

求证：

证明：①当n=1时，左边＝　右边＝，等式成立.

　　　②设n=k时，有

　 那么，当n=k+1时，有

 ，即n=k+1时，命题成立

根据①②可知，对n∈N^＊，等式成立.

设计意图：练习题1，2的证明难度不大，套用数学归纳法的证明步骤不难解答，通过这两个练习能看到学生对数学归纳法证题步骤的掌握情况．这样既可以检验学生的学习水平，保证不盲目拔高，同时不冲淡本节课的重点，对例题是一个很好的对比与补充．通过3，4的易错辨析，进一步体会数学归纳法证题时的两个步骤、一个结论，“递推基础不可少，归纳假设要用到，结论写明莫忘掉”.

八、总结归纳，加深理解

1、本节课的中心内容是归纳法和数学归纳法；

2、归纳法是一种由特殊到一般的推理方法，它可以分为完全归纳法和不完全归纳法两种，枚举法仅局限于有限个元素，而不完全归纳法得出的结论不一定具有可靠性，数学归纳法属于完全归纳法；

3、数学归纳法作为一种证明方法，其基本思想是递推(递归)思想，使用要点可概括为：两个步骤一结论，递推基础不可少，归纳假设要用到，结论写明莫忘掉；

4、本节课所涉及到的数学思想方法有：递推思想、类比思想、分类思想、归纳思想、辩证思想．

九、布置作业, 课外延伸

十、书面作业：见教材P₅₆

     课后思考题：

1. 是否存在常数a、b、c使得等式：

对一切自然数n都成立并证明你的结论.

2.是否存在常数a、b、c，使得等式1

对一切自然数n都成立？并证明你的结论（a=3,b=11,c=10）

设计意图: 思考题则起着承上启下的作用,  它既是“观察—归纳—猜想—证明”的完整思维探究过程的再体验，也是对下节课内容的铺垫与伏笔．