理科数学归纳法知识总结
理科数学归纳法知识总结
一基本概念
1.运用数学归纳法证明命题要分两步,
第一步是归纳奠基(或递推基础),
第二步是归纳递推(或归纳假设),
两步缺一不可
二 易错点
1.归纳起点易错
(1)n未必是从n=1开始
例 用数学归纳法证明:凸n边形的对角线条数为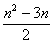
点拔:本题的归纳起点n=3
(2) n=1时的表达式
例 用数学归纳法证明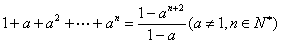 ,在验证n=1时,左边计算所得的式子是( )
,在验证n=1时,左边计算所得的式子是( )
A. 1 B.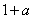 C.
C.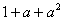 D.
D. 
点拨 n=1时,左边的最高次数为1,即最后一项为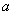 ,左边是
,左边是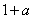 ,故选B
,故选B
2.没有运用归纳假设的证明不是数学归纳法
例1 用数学归纳法证明: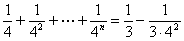
错证:
(1)当n=1时,左=右=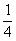 1,等式成立
1,等式成立
(2)假设当n=k时等式成立,
则当n=k+1时,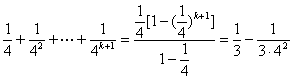
综合(1)(2),等式对所有正整数都成立
点拨:错误原因在于只有数学归纳法的形式,没有数学归纳法的“实质”即在归纳递推中,没有运用归纳假设
3 从n=k到n=k+1增加项错误
例1 已知n是正偶数,用数学归纳法证明时,若已假设n=k(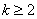 且为偶数)时命题为真,,则还需证明( )
且为偶数)时命题为真,,则还需证明( )
A.n=k+1时命题成立 B. n=k+2时命题成立
C. n=2k+2时命题成立 D. n=2(k+2)时命题成立
点拨:因n是正偶数,故只需证等式对所有偶数都成立,因k的下一个偶数是k+2,故选
例2 用数学归纳法证明不等式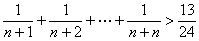 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是
点拨:求 即可
即可
当 n=k时, 左边 ,
,
n=k+1时,左边 ,
,
故左边增加的式子是 ,即
,即
三 知识应用
用数学归纳法可以证明许多与自然数有关的数学命题,其中包括恒等式、不等式、数列通项公式、整除性问题、几何问题等
1 用数学归纳法证明等式
例1 用数学归纳法证明等式:
证明:(1)当n=1时,左= =右,等式成立
=右,等式成立
(2)假设当n=k时等式成立,即
则n=k+1时

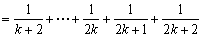
 当n=k+1时,等式也成立
当n=k+1时,等式也成立
综合(1)(2),等式对所有正整数都成立
例2 用数学归纳法证明:
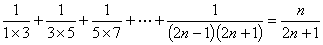
证明:(1)当n=1时,左边 ,右边
,右边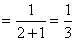 ,左边=右边,等式成立.
,左边=右边,等式成立.
(2)假设n=k时,等式成立,即:

则当n=k+1时.




 当n=k+1时,等式也成立
当n=k+1时,等式也成立
综合(1)(2),等式对所有正整数都成立
2 用数学归纳法证明不等式
例1 用数学归纳法证明不等式
证明:(1)当n=1时,左边= ,右边=2,不等式成立
,右边=2,不等式成立
(2)假设当n=k时不等式成立,
即
则当n=k+1时
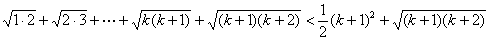


 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立
综合(1)(2),不等式对所有正整数都成立
注意(1)数学归纳法证明命题,格式严谨,必须严格按步骤进行;
(2)归纳递推是证明的难点,应看准“目标”进行变形;
(3)由k推导到k+1时,有时可以“套”用其它证明方法,如:比较法、分析法等,表现出数学归纳法“灵活”的一面
例2.证明不等式 (n∈N).
(n∈N).
证明:(1)当n=1时,左边=1,右边=2.
左边<右边,不等式成立.
(2)假设n=k时,不等式成立,
即 .
.
则当n=k+1时,



 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立
综合(1)(2),不等式对所有正整数都成立
3 用数学归纳法证明整除问题
例1 求证: 能被6 整除.
能被6 整除.
证明:(1)当 时,13+5×1=6能被6整除,命题正确;
时,13+5×1=6能被6整除,命题正确;
(2)假设 时命题正确,即
时命题正确,即 能被6整除,
能被6整除,
则当 时,
时,
 ,
,
∵两个连续的整数的乘积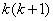 是偶数,
是偶数, 能被6整除,
能被6整除,
 能被6整除,即当
能被6整除,即当 时命题也正确,
时命题也正确,
 当n=k+1时, 命题也成立
当n=k+1时, 命题也成立
综合(1)(2),命题对所有正整数都成立
例2 证明: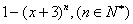 能被
能被 整除
整除
证明:(1)当n=1时, ,能被
,能被 整除;
整除;
(2)假设n=k 时命题成立,即
时命题成立,即 能被
能被 整除
整除
可设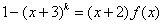 (其中
(其中 为
为 次多项式)
次多项式)
则当n=k+1时,

能被 整除
整除
 当n=k+1时, 命题也成立
当n=k+1时, 命题也成立
综合(1)(2),命题对所有正整数都成立
4 用“归纳——猜想——证明”解决数列问题
例1 在数列 中,
中,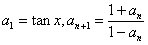 ,
,
(1)写出
 ;(2)求数列
;(2)求数列 的通项公式
的通项公式
解:(1)
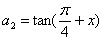 ,
,
 ,
,
猜想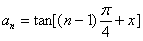
下面用数学归纳法证明:
(1)当n=1时,由上面的探求可知猜想成立
(2)假设n=k时猜想成立,即
则n=k+1时 
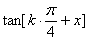
 当n=k+1时, 猜想也成立
当n=k+1时, 猜想也成立
综合(1)(2),猜想对所有正整数都成立
例2 在数列 中,
中,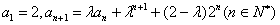 ,其中
,其中 ,求数列
,求数列 的通项公式
的通项公式
解: ,
, ,
, .
.
由此可猜想出数列 的通项公式为
的通项公式为 .
.
以下用数学归纳法证明:
(1) 当n=1时, ,等式成立.
,等式成立.
(2)假设当n=k时等式成立,
即 .
.
则当n=k+1时,

 当n=k+1时, 猜想也成立
当n=k+1时, 猜想也成立
综合(1)(2),数列 的通项公式
的通项公式

5用“归纳——猜想——证明”解决几何问题
例1.n个半圆的圆心在同一条直线l上,这n个半圆每两个都相交,且都在直线l的同侧,问这些半圆被所有的交点最多分成多少段圆弧?
分析:设这些半圆最多互相分成f (n)段圆弧,采用由特殊到一般的方法,进行猜想和论证.
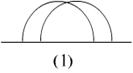

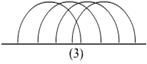
当n=2时,由图(1).两个半圆交于一点,则分成4段圆弧,故f (2)=4=22.
当n=3时,由图(2).三个半径交于三点,则分成9段圆弧,故f (3)=9=32.
由n=4时,由图(3).三个半圆交于6点,则分成16段圆弧,故f (4)=16=42.
由此猜想满足条件的n个半圆互相分成圆弧段有f (n)=n2.
用数学归纳法证明如下:
(1)当n=2时,上面已证.
(2)设n=k时,猜想成立,即f (k)=k2,
则当n=k+1时,第k+1个半圆与原k个半圆均相交,为获得最多圆弧,任意三个半圆不能交于一点,所以第k+1个半圆把原k个半圆中的每一个半圆中的一段弧分成两段弧,这样就多出k条圆弧;另外原k个半圆把第k+1个半圆分成k+1段,这样又多出了k+1段圆弧.
∴ f (k+1)=k2+k+(k+1)
=k2+2k+1=(k+1)2
∴ 满足条件的k+1个半圆被所有的交点最多分成(k+1)2段圆弧.
 当n=k+1时, 猜想也成立
当n=k+1时, 猜想也成立
综合(1)(2)知 满足条件的n个半圆被所有的交点最多分成n2段圆弧.
四 练习巩固
1.用数学归纳法证明:1(n2-1)+2(n2-22)+…+n(n2-n2)= (n∈N*).
(n∈N*).
2.用数学归纳法证明:1·2·3+2·3·4+…+n(n+1)(n+2)=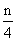 (n+1)·( n+2)·(n+3)(n∈N*).
(n+1)·( n+2)·(n+3)(n∈N*).
3.当n>1,n∈N*时,求证:
4.用数学归纳法证明: (n∈N*)
(n∈N*)
5.用数学归纳法证明 49n+16n-1能被64整除(n∈N*)
6.用数学归纳法证明 mn+2+(m+1)2n+1能被m2+m+1整除(n∈N*)
7.在数列 中,an>0,且Sn=1/2(an+
中,an>0,且Sn=1/2(an+ )
)
(1)求a1、a2、a3;
(2)猜测出an的关系式并用数学归纳法证明。
8.设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(1)求a1,a2;(2)猜想数列{Sn}的通项公式,并给出严格的证明.
9.平面内有n个圆,其中每两个圆都相交于两点,且每三个圆都不相交于同一点,求证:这n个圆把平面分成n2-n+2个部分。
第二篇:高二理科数学期末知识总结(2-2,2-3)
高二第二学期理科数学总结
一、导数
1、导数定义:f(x)在点x0处的导数记作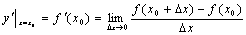 ;
;
2、几何意义:切线斜率;物理意义:瞬时速度;
3、常见函数的导数公式:
①
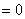 ;②
;② ;③
;③ ;④
;④ ;
;
⑤ ;⑥
;⑥ ;⑦
;⑦ ;⑧
;⑧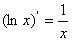 。
。
⑨ ;⑩
;⑩
4、导数的四则运算法则:
5、复合函数的导数:
6、导数的应用:
(1)利用导数求切线:根据导数的几何意义,求得该点的切线斜率为该处的导数(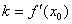 );利用点斜式(
);利用点斜式( )求得切线方程。
)求得切线方程。
注意ⅰ)所给点是切点吗?ⅱ)所求的是“在”还是“过”该点的切线?
(2)利用导数判断函数单调性:① 是增函数;
是增函数;
② 为减函数;③
为减函数;③ 为常数;
为常数;
反之,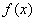 是增函数
是增函数
 ,
,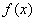 是减函数
是减函数

(3)利用导数求极值:ⅰ)求导数 ;ⅱ)求方程
;ⅱ)求方程 的根;ⅲ)列表得极值。
的根;ⅲ)列表得极值。
(4)利用导数最大值与最小值:
ⅰ)求得极值;ⅱ)求区间端点值(如果有);ⅲ得最值。
(5)求解实际优化问题:
①根据所求假设未知数 和
和 ,并由题意找出两者的函数关系式,同时给出
,并由题意找出两者的函数关系式,同时给出 的范围;②求导,令其为0,解得
的范围;②求导,令其为0,解得 值,舍去不符合要求的值;
值,舍去不符合要求的值;
③根据该值两侧的单调性,判断出最值情况(最大还是最小?);
④求最值(题目需要时);回归题意,给出结论;
7、定积分
⑴定积分的定义: (注意整体思想)
(注意整体思想)
⑵定积分的性质:① (
(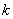 常数);
常数);
② ;
;
③ (其中
(其中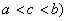 。(分步累加)
。(分步累加)
⑶微积分基本定理(牛顿—莱布尼兹公式):
(熟记 (
( ),
),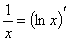 ,
,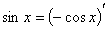 ,
,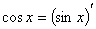 ,
, ,
,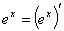 )
)
⑷定积分的应用:
①求曲边梯形的面积: (两曲线所围面积);
(两曲线所围面积);
注意:若是单曲线 与x轴所围面积,位于x轴下方的需在定积分式子前加“—”
与x轴所围面积,位于x轴下方的需在定积分式子前加“—”
②求变速直线运动的路程: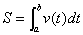 ;
;
③求变力做功: 。
。
二、复数
1.概念:
⑴z=a+bi∈R b=0 (a,b∈R)
b=0 (a,b∈R) z=
z=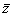
 z2≥0;
z2≥0;
⑵z=a+bi是虚数 b≠0(a,b∈R);
b≠0(a,b∈R);
⑶z=a+bi是纯虚数 a=0且b≠0(a,b∈R)
a=0且b≠0(a,b∈R) z+
z+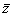 =0(z≠0)
=0(z≠0) z2<0;
z2<0;
⑷a+bi=c+di a=c且c=d(a,b,c,d∈R);
a=c且c=d(a,b,c,d∈R);
2.复数的代数形式及其运算:设z1= a + bi , z2 = c + di (a,b,c,d∈R),则:
⑴z 1± z2 = (a + b) ± (c + d)i;⑵ z1.z2 = (a+bi)·(c+di)=(ac-bd)+ (ad+bc)i;
⑶z1÷z2 =
 (z2≠0) (分母实数化);
(z2≠0) (分母实数化);
3.几个重要的结论:

 ;
;
 (3)
(3) ;
;
(4)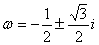 以3为周期,且
以3为周期,且 ;
; =0;
=0;
(5) 。
。
4.复数的几何意义
(1)复平面、实轴、虚轴
(2)复数
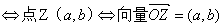
三、推理与证明
(一).推理:
⑴合情推理:归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理。
①归纳推理:由某类食物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者有个别事实概括出一般结论的推理,称为归纳推理,简称归纳。
注:归纳推理是由部分到整体,由个别到一般的推理。
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比啊啊啊啊啊啊啊啊啊啊啊啊啊啊。
注:类比推理是特殊到特殊的推理啊啊啊啊啊啊啊啊啊啊啊。
⑵演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理。
注:演绎推理是由一般到特殊的推理。
“三段论”是演绎推理的一般模式,包括:⑴大前提---------已知的一般结论;⑵小前提---------所研究的特殊情况;⑶结 论---------根据一般原理,对特殊情况得出的判断。
(二)证明
⒈直接证明
⑴综合法
一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。
⑵分析法
一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。
2.间接证明------反证法
一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法。
(三)数学归纳法
一般的证明一个与正整数 有关的一个命题,可按以下步骤进行:
有关的一个命题,可按以下步骤进行:
⑴证明当 取第一个值
取第一个值 是命题成立;
是命题成立;
⑵假设当 命题成立,证明当
命题成立,证明当 时命题也成立。
时命题也成立。
那么由⑴⑵就可以判定命题对从 开始所有的正整数都成立。
开始所有的正整数都成立。
注:①数学归纳法的两个步骤缺一不可,用数学归纳法证明问题时必须严格按步骤进行;
①  的取值视题目而定,可能是1,也可能是2等。
的取值视题目而定,可能是1,也可能是2等。
四、排列、组合和二项式定理
⑴排列数公式: =n(n-1)(n-2)…(n-m+1)=
=n(n-1)(n-2)…(n-m+1)= (m≤n,m、n∈N*),当m=n时为全排列
(m≤n,m、n∈N*),当m=n时为全排列 =n(n-1)(n-2)…3.2.1=n!,
=n(n-1)(n-2)…3.2.1=n!, ;
;
⑵组合数公式: (m≤n),
(m≤n), ;
;
⑶组合数性质: ;
; ;
;
⑷二项式定理:
①通项: ②注意二项式系数与系数的区别;
②注意二项式系数与系数的区别;
⑸二项式系数的性质:
①与首末两端等距离的二项式系数相等(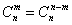 );
);
②若n为偶数,中间一项(第 +1项)二项式系数(
+1项)二项式系数( )最大;若n为奇数,中间两项(第
)最大;若n为奇数,中间两项(第 +1和
+1和 +1项)二项式系数(
+1项)二项式系数(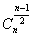 ,
, )最大;
)最大;
③
(6)求二项展开式各项系数和或奇(偶)数项系数和时,注意运用代入法(取 )。
)。
五.概率与统计
⑴随机变量的分布列:
(求解过程:直接假设随机变量啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊,找其可能取值,求对应概率,列表)
①随机变量分布列的性质: ,i=1,2,…; p1+p2+…=1;
,i=1,2,…; p1+p2+…=1;
②离散型随机变量:

期望:EX=x1p1 + x2p2 + … + xnpn +… ;
方差:DX=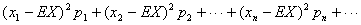 ;
;
注: ;
;




 ③两点分布(0—1分布):
③两点分布(0—1分布):
 X 0 1 期望:EX=p;方差:DX=p(1-p).
X 0 1 期望:EX=p;方差:DX=p(1-p).
P 1-p p
 ④超几何分布:
④超几何分布:
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则 其中,
其中, 。
。
称分布列
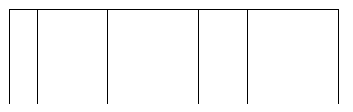
X 0 1 … m
 P
P 
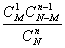 …
… 
 为超几何分布列, 称X服从超几何分布。
为超几何分布列, 称X服从超几何分布。
⑤二项分布(n次独立重复试验):
若X~B(n,p),则EX=np, DX=np(1- p);注: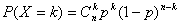 。
。
⑵条件概率:
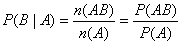 ,称为在事件A发生的条件下,事件B发生的概率。
,称为在事件A发生的条件下,事件B发生的概率。
注:①0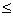 P(B|A)
P(B|A)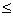 1;②P(B∪C|A)=P(B|A)+P(C|A)。
1;②P(B∪C|A)=P(B|A)+P(C|A)。
⑶独立事件同时发生的概率:P(AB)=P(A)P(B)。
⑷正态总体的概率密度函数: 式中
式中 (
( )是参数,分别表示总体的平均数(期望值)与标准差;
)是参数,分别表示总体的平均数(期望值)与标准差;
⑸正态曲线的性质:
①曲线位于x轴上方,与x轴不相交啊啊啊啊啊啊啊啊;②曲线是单峰的,关于直线x=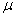 对称;
对称;
③曲线在x=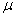 处达到峰值
处达到峰值 ;④曲线与x轴之间的面积为1;
;④曲线与x轴之间的面积为1;
⑹ ,则
,则
① 曲线的对称轴随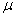 的变化沿x轴平移,
的变化沿x轴平移,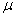 变大,曲线右移;
变大,曲线右移;
② 曲线高矮由 确定:
确定: 越大,曲线越“矮胖”, 反之,曲线越“高瘦”;
越大,曲线越“矮胖”, 反之,曲线越“高瘦”;
⑺标准正态分布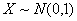 ,其中
,其中
注:P =0.9974 (
=0.9974 ( 原则)
原则)
⑻线性回归方程 ,其中
,其中 ,
, ,
,
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…
-
化学复习善用总结归纳法
强化知识体系结构在复习元素化合物知识应从组成———结构入手,抓住组成和结构决定物质性质这一关键,按类别复习物质的性质、用途及制备等…